三年级下册数学课件-7.8 数学广场-放苹果沪教版 18张ppt
文档属性
| 名称 | 三年级下册数学课件-7.8 数学广场-放苹果沪教版 18张ppt |
|
|
| 格式 | ppt | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
至少有一种花色的牌不止1张。
在52张牌中(拿掉大王和小王)任取5张。
至少有一种点数的牌不止1张。
在52张牌中(拿掉大王和小王)任取14张。
把3个苹果放入2个抽屉。
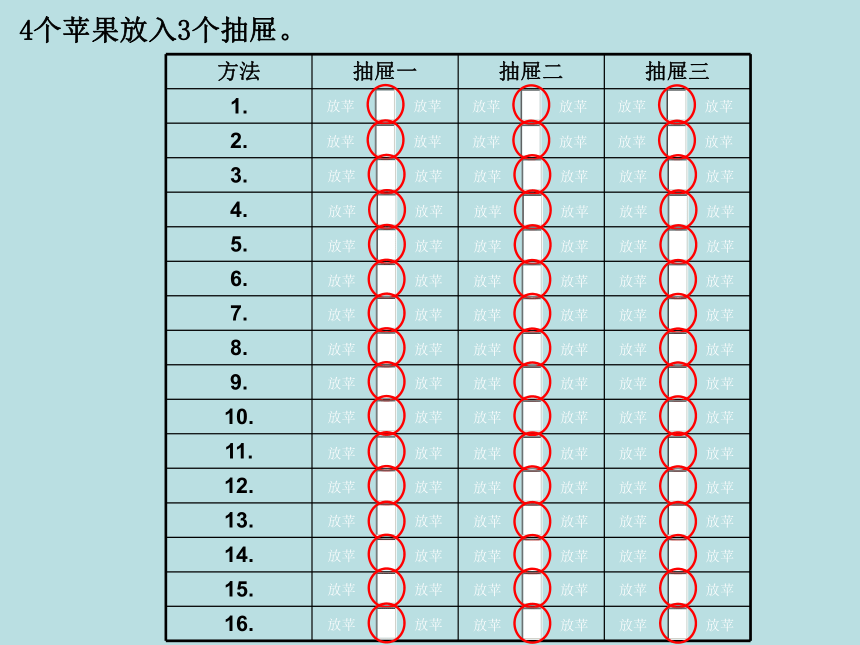
4个苹果放入3个抽屉。
方法
抽屉一
抽屉二
抽屉三
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
最先发现这些规律的人是德国数学家——狄里克雷,人们为了纪念他从这么平凡的事情中发现的规律,就把这个规律用他的名字命名,叫“狄里克雷原理”,又把它叫做“鸽巢原理”,或者“抽屉原理”。
之所以把这个规律称之为“原理”,是因为在我们的生活中存在着许多能用这个原理解决的问题,研究出这个规律是非常有价值的。
在52张牌中(拿掉大王和小王)任取5张。
5张牌
5只苹果
4种花色
4只抽屉
牌的张数
=
花色数
+
1
至少有一种花色的牌不止1张。
在52张牌中(拿掉大王和小王)任取14张。
14张牌
14只苹果
13种点数
13只抽屉
牌的张数
=
点数
+
1
至少有一种点数的牌不止1张。
教室里有4名学生正在数学,英语,语文,3科作业,这4名学生中,至少有两个人在做同一科作业,这句话对吗?
4名学生
4只苹果
3科作业
3只抽屉
学生人数
=
作业科目+1
答:至少有两个人在做同一科作业。
一年有12个月,想一想至少要多少人,一定有2个或2个以上的人生日是同一个月的?
12个月
12只抽屉
学生人数
苹果数
学生人数
=
月份数
+
1
12
+
1
=
13(人)
答:至少要13人,一定要有2个或2个以上的人生日是同一个月的。
1.把51个苹果放进50个抽屉里,不论怎么放,至少有一个抽屉里不止有(
)个苹果。
A、51
B、50
C、1
D、2
选择题。
C
苹果数=抽屉数+1
2.至少有(
)只鸽子任意飞入5个鸽舍,才会出现必有一个鸽舍里至少飞入2只鸽子。
A、5
B、6
C、1
D、2
B
5个鸽舍
5只抽屉
鸽子数
苹果数
鸽子数=鸽舍数+1
5
+
1
=
6(只)
选择题。
3.在最多(
)个花瓶内任意插入12朵菊花,那么至少有一个花瓶内插入2朵鲜花。
A、11
B、12
C、1
D、2
A
12朵菊花
12只苹果
花瓶数
抽屉数
菊花数
=
花瓶数
+
1
12
–
1
=
11(只)
选择题。
圣诞节快到了,圣诞老人来给大家送礼物。他的背包里有三种不同颜色的筷子,至少要拿出几只筷子才能配出一付同样颜色的筷子?
3
+
1
=
4(只)
答:至少要拿出4只筷子才能配出一付同样颜色的筷子。
圣诞老人的背包里还有三种不同颜色的手套,至少要拿出几只手套才能配出一付同样颜色的手套?
3×2
+
1
=
7(只)
答:至少要拿出7只手套才能配出一付同样颜色的手套。
将5个汉堡放入2个盘子里,有几种不同的放法?你发现了什么?
方法
蓝盘子
绿盘子
1.
2.
3.
4.
5.
6.
7.
将2根萝卜放入3个盘子里,有几种不同的放法?你发现了什么?
方法
红盘子
蓝盘子
绿盘子
1.
2.
3.
4.
5.
6.
7.
至少有一种花色的牌不止1张。
在52张牌中(拿掉大王和小王)任取5张。
至少有一种点数的牌不止1张。
在52张牌中(拿掉大王和小王)任取14张。
把3个苹果放入2个抽屉。
4个苹果放入3个抽屉。
方法
抽屉一
抽屉二
抽屉三
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
放苹
最先发现这些规律的人是德国数学家——狄里克雷,人们为了纪念他从这么平凡的事情中发现的规律,就把这个规律用他的名字命名,叫“狄里克雷原理”,又把它叫做“鸽巢原理”,或者“抽屉原理”。
之所以把这个规律称之为“原理”,是因为在我们的生活中存在着许多能用这个原理解决的问题,研究出这个规律是非常有价值的。
在52张牌中(拿掉大王和小王)任取5张。
5张牌
5只苹果
4种花色
4只抽屉
牌的张数
=
花色数
+
1
至少有一种花色的牌不止1张。
在52张牌中(拿掉大王和小王)任取14张。
14张牌
14只苹果
13种点数
13只抽屉
牌的张数
=
点数
+
1
至少有一种点数的牌不止1张。
教室里有4名学生正在数学,英语,语文,3科作业,这4名学生中,至少有两个人在做同一科作业,这句话对吗?
4名学生
4只苹果
3科作业
3只抽屉
学生人数
=
作业科目+1
答:至少有两个人在做同一科作业。
一年有12个月,想一想至少要多少人,一定有2个或2个以上的人生日是同一个月的?
12个月
12只抽屉
学生人数
苹果数
学生人数
=
月份数
+
1
12
+
1
=
13(人)
答:至少要13人,一定要有2个或2个以上的人生日是同一个月的。
1.把51个苹果放进50个抽屉里,不论怎么放,至少有一个抽屉里不止有(
)个苹果。
A、51
B、50
C、1
D、2
选择题。
C
苹果数=抽屉数+1
2.至少有(
)只鸽子任意飞入5个鸽舍,才会出现必有一个鸽舍里至少飞入2只鸽子。
A、5
B、6
C、1
D、2
B
5个鸽舍
5只抽屉
鸽子数
苹果数
鸽子数=鸽舍数+1
5
+
1
=
6(只)
选择题。
3.在最多(
)个花瓶内任意插入12朵菊花,那么至少有一个花瓶内插入2朵鲜花。
A、11
B、12
C、1
D、2
A
12朵菊花
12只苹果
花瓶数
抽屉数
菊花数
=
花瓶数
+
1
12
–
1
=
11(只)
选择题。
圣诞节快到了,圣诞老人来给大家送礼物。他的背包里有三种不同颜色的筷子,至少要拿出几只筷子才能配出一付同样颜色的筷子?
3
+
1
=
4(只)
答:至少要拿出4只筷子才能配出一付同样颜色的筷子。
圣诞老人的背包里还有三种不同颜色的手套,至少要拿出几只手套才能配出一付同样颜色的手套?
3×2
+
1
=
7(只)
答:至少要拿出7只手套才能配出一付同样颜色的手套。
将5个汉堡放入2个盘子里,有几种不同的放法?你发现了什么?
方法
蓝盘子
绿盘子
1.
2.
3.
4.
5.
6.
7.
将2根萝卜放入3个盘子里,有几种不同的放法?你发现了什么?
方法
红盘子
蓝盘子
绿盘子
1.
2.
3.
4.
5.
6.
7.
