2020-2021学年湖南省邵阳市绥宁县八年级(下)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年湖南省邵阳市绥宁县八年级(下)期末数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 892.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览

文档简介
2020-2021学年湖南省邵阳市绥宁县八年级(下)期末数学试卷
一、选择题(共10小题,共30分).
1.在平面直角坐标系中,点(2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.五边形的内角和是( )
A.180° B.360° C.540° D.720°
3.下列图形中,是中心对称图形的有( )
A.4个 B.3个 C.2个 D.1个
4.直角三角形两直角边长为5和12,则此直角三角形斜边上的中线的长是( )
A.5 B.6 C.6.5 D.13
5.一个人做“抛硬币”的游戏,正面出现4次,反面出现了6次,正确说法为( )
A.出现正面的频率是4 B.出现反面的频率是6
C.出现反面的频率是60% D.出现正面的频数是40%
6.在平面直角坐标系中,将直线l1:y=3x平移后得到直线l2:y=3x+2,则下列平移的做法正确的是( )
A.将l1向左平移2个单位 B.将l1向右平移2个单位
C.将l1向上平移2个单位 D.将l1向下平移2个单位
7.关于函数y=﹣2x+1,下列结论正确的是( )
A.图象必经过(﹣2,1)
B.y随x的增大而增大
C.图象经过第一、二、三象限
D.当x>时,y<0
8.下列说法错误的是( )
A.△ABC中,若有∠A+∠B=∠C,则△ABC是直角三角形
B.△ABC中,若有∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
C.△ABC的三边长分别为:a,b,c,且a2﹣b2=c2,则△ABC是直角三角形
D.在一个直角三角形中,有两边的长度分别是3和5,则第三边的长度是4
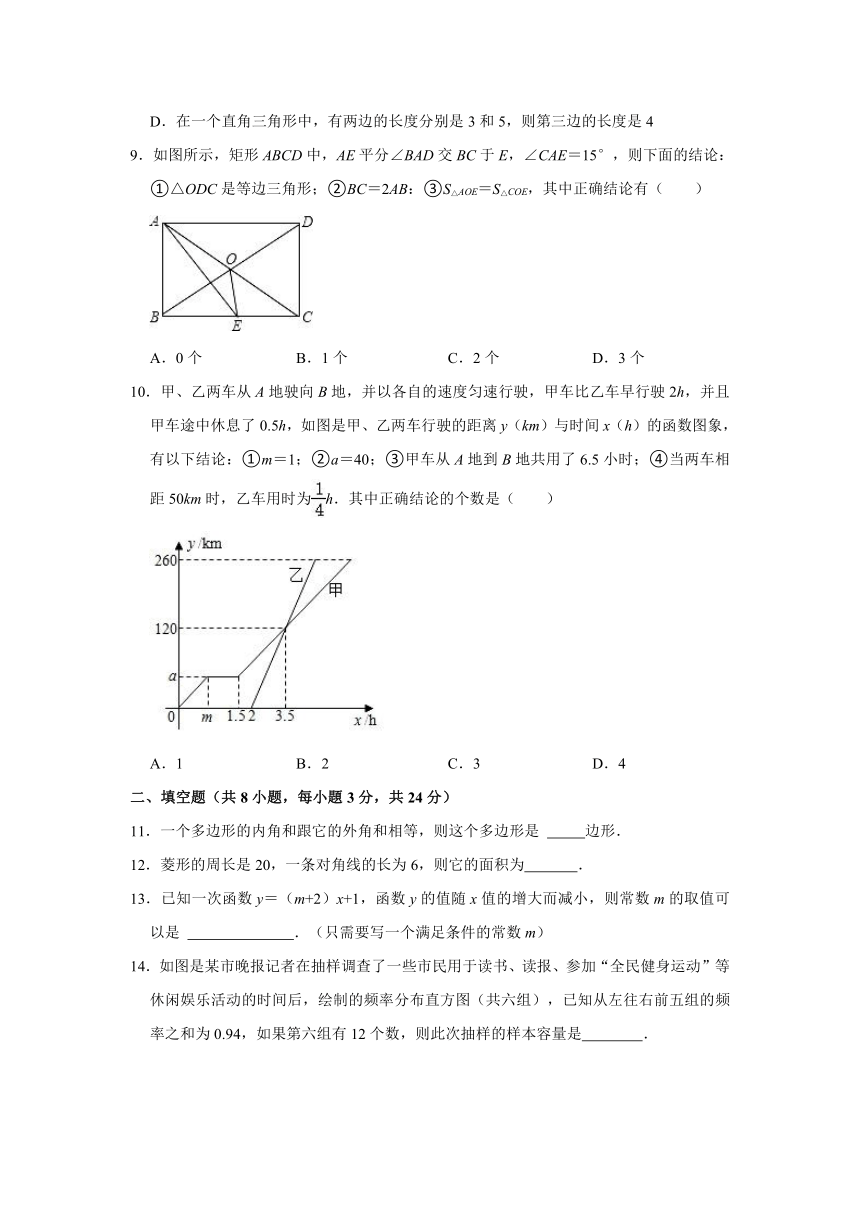
9.如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:①△ODC是等边三角形;②BC=2AB:③S△AOE=S△COE,其中正确结论有( )
A.0个 B.1个 C.2个 D.3个
10.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象,有以下结论:①m=1;②a=40;③甲车从A地到B地共用了6.5小时;④当两车相距50km时,乙车用时为h.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(共8小题,每小題3分,共24分)
11.一个多边形的内角和跟它的外角和相等,则这个多边形是 边形.
12.菱形的周长是20,一条对角线的长为6,则它的面积为 .
13.已知一次函数y=(m+2)x+1,函数y的值随x值的增大而减小,则常数m的取值可以是 .(只需要写一个满足条件的常数m)
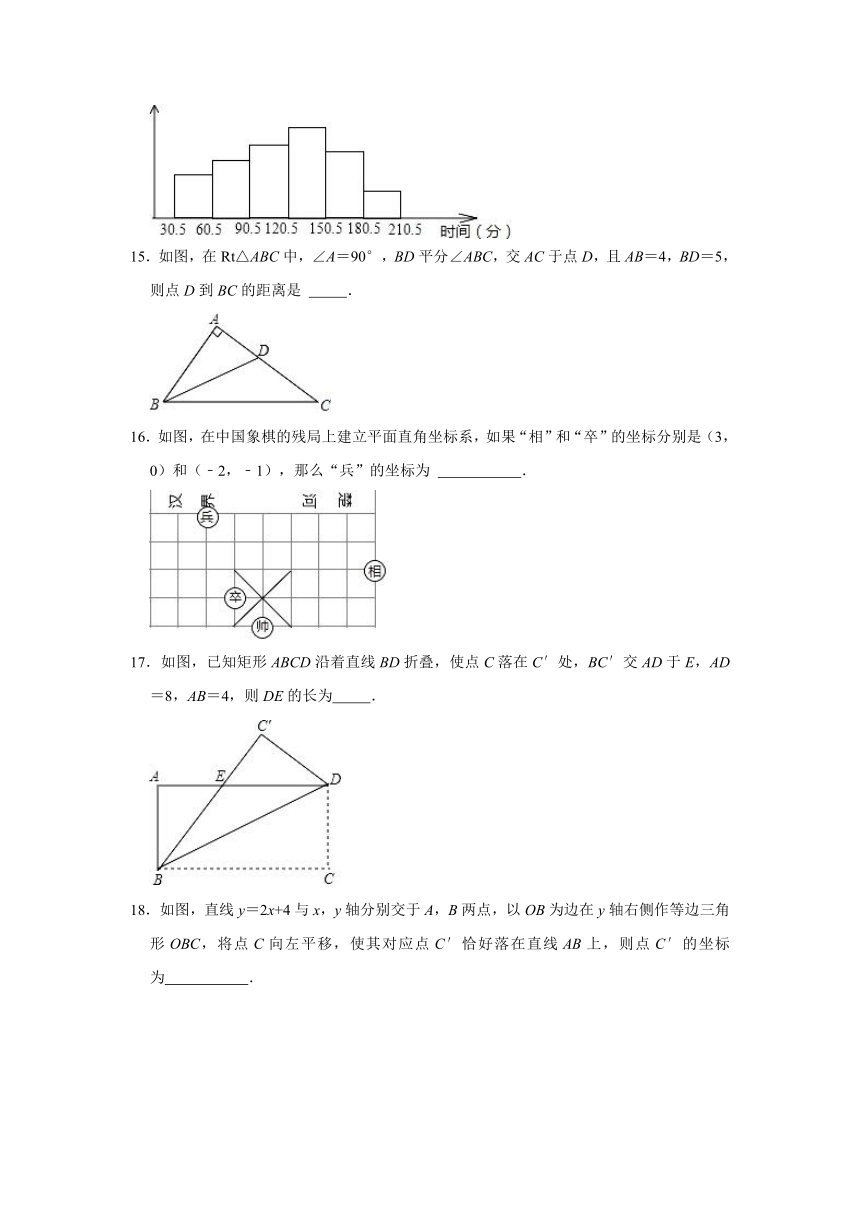
14.如图是某市晚报记者在抽样调查了一些市民用于读书、读报、参加“全民健身运动”等休闲娱乐活动的时间后,绘制的频率分布直方图(共六组),已知从左往右前五组的频率之和为0.94,如果第六组有12个数,则此次抽样的样本容量是 .
15.如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是 .
16.如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“卒”的坐标分别是(3,0)和(﹣2,﹣1),那么“兵”的坐标为 .
17.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为 .
18.如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .
三、解答题(本大题共8小題,66分。其中:第19至25小題各8分:第26小题10分)
19.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,AC=6,BD=9,CD=5,试求△COD的周长.
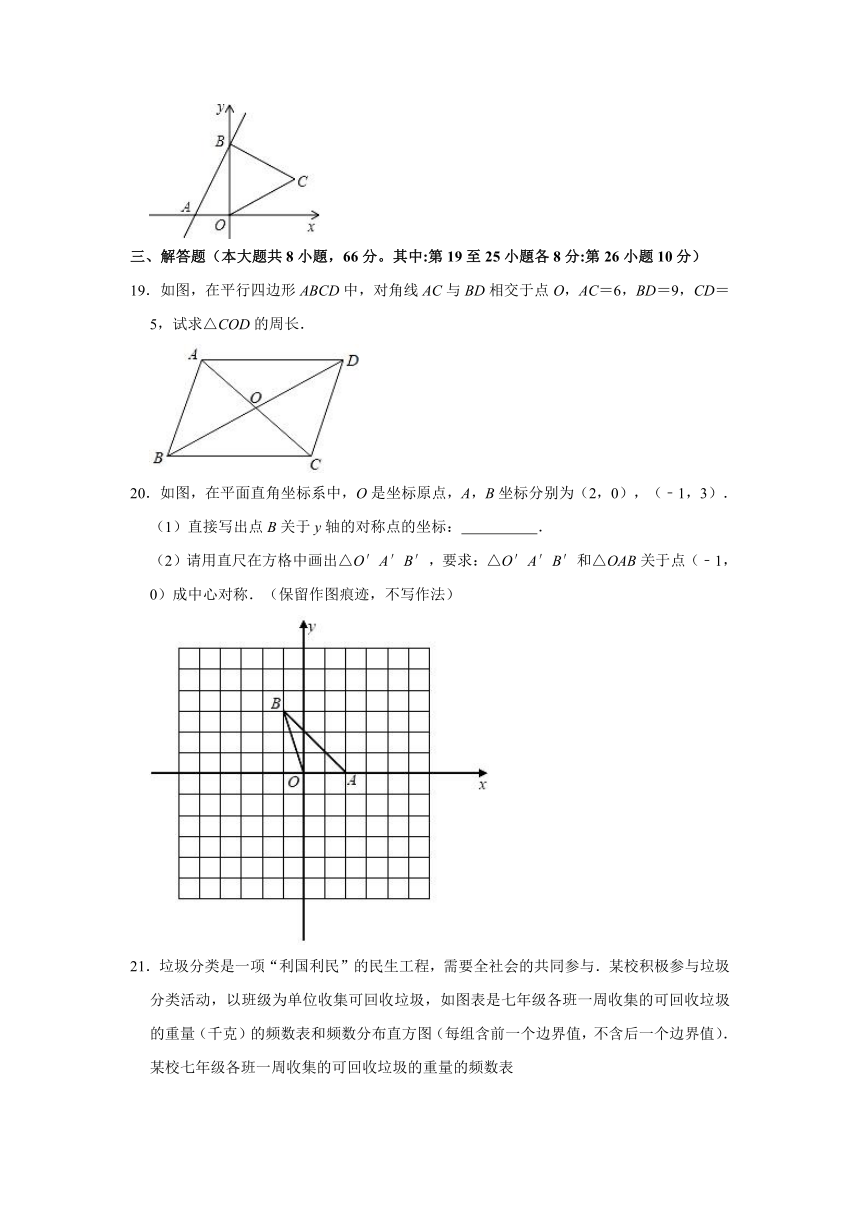
20.如图,在平面直角坐标系中,O是坐标原点,A,B坐标分别为(2,0),(﹣1,3).
(1)直接写出点B关于y轴的对称点的坐标: .
(2)请用直尺在方格中画出△O′A′B′,要求:△O′A′B′和△OAB关于点(﹣1,0)成中心对称.(保留作图痕迹,不写作法)
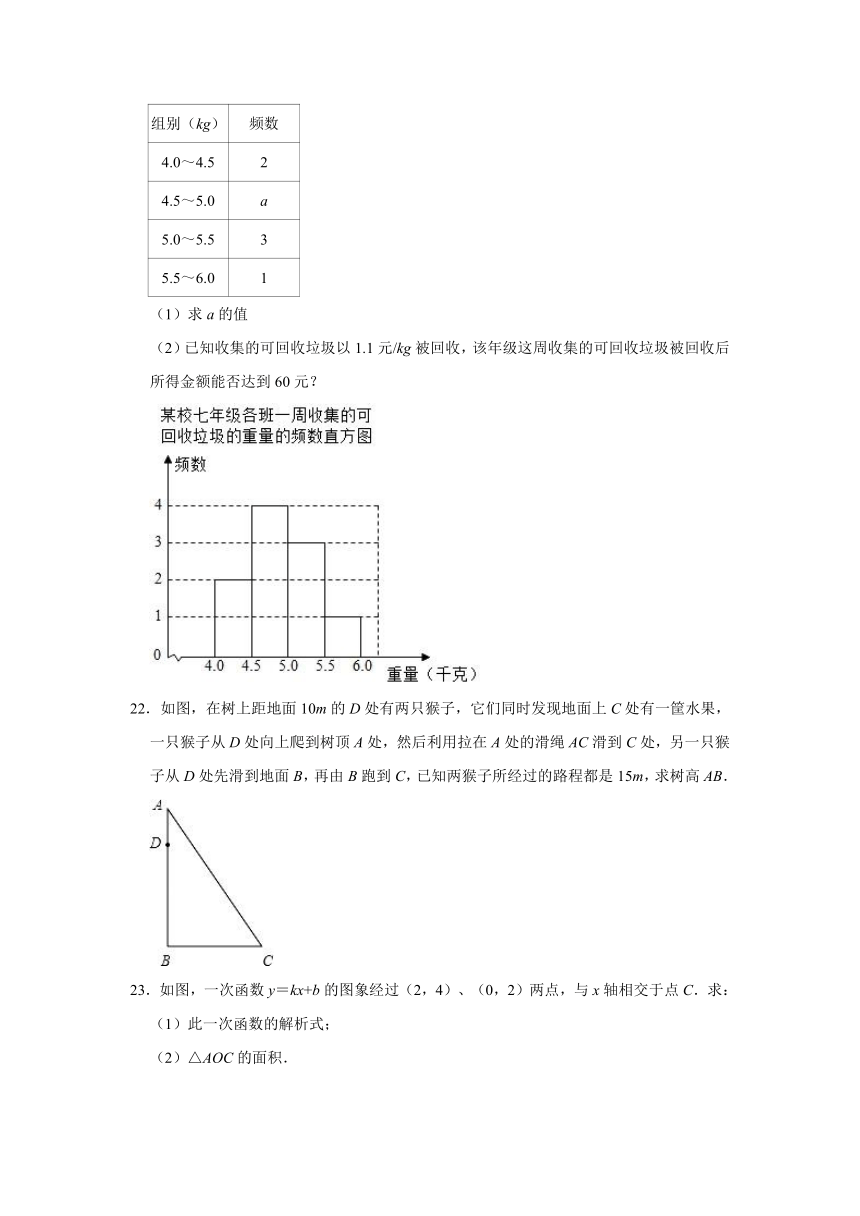
21.垃圾分类是一项“利国利民”的民生工程,需要全社会的共同参与.某校积极参与垃圾分类活动,以班级为单位收集可回收垃圾,如图表是七年级各班一周收集的可回收垃圾的重量(千克)的频数表和频数分布直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的重量的频数表
组别(kg) 频数
4.0~4.5 2
4.5~5.0 a
5.0~5.5 3
5.5~6.0 1
(1)求a的值
(2)已知收集的可回收垃圾以1.1元/kg被回收,该年级这周收集的可回收垃圾被回收后所得金额能否达到60元?
22.如图,在树上距地面10m的D处有两只猴子,它们同时发现地面上C处有一筐水果,一只猴子从D处向上爬到树顶A处,然后利用拉在A处的滑绳AC滑到C处,另一只猴子从D处先滑到地面B,再由B跑到C,已知两猴子所经过的路程都是15m,求树高AB.
23.如图,一次函数y=kx+b的图象经过(2,4)、(0,2)两点,与x轴相交于点C.求:
(1)此一次函数的解析式;
(2)△AOC的面积.
24.如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.
25.某水果店以每千克8元的价格购进苹果若干千克,销售了部分苹果后,余下的苹果每千克降价4元销售,全部售完.销售金额y(元)与销售量x(千克)之间的关系如图所示,请根据图象提供的信息完成下列问题:
(1)降价前苹果的销售单价是 元/千克;
(2)求降价后销售金额y(元)与销售量x(千克)之间的函数解析式,并写出自变量的取值范围;
(3)该水果店这次销售苹果盈利了多少元?
26.某校八年级数学学习小组在探究学习的过程中,用两块完全相同的且含60°角(∠ABC=∠AFE=60°)的直角三角板ABC与AFE按①所示的方式放置.现将Rt△AEF绕直角顶点A按逆时针方向旋转∠a(0°<α<90°),如图②,AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角∠α=30°时,四边形ABPF是什么样的特殊四边形?说明理由.
参考答案
一、选择题(共10小题,每小题3分,共30分)请将正确答案序号填写在答题卡上
1.在平面直角坐标系中,点(2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:在平面直角坐标系中,点(2,1)的横坐标和纵坐标都大于0,所以点(2,1)在第一象限.
故选:A.
2.五边形的内角和是( )
A.180° B.360° C.540° D.720°
解:五边形的内角和是:
(5﹣2)×180°
=3×180°
=540°
故选:C.
3.下列图形中,是中心对称图形的有( )
A.4个 B.3个 C.2个 D.1个
解:从左到右,第一、第二、第三个图形是中心对称图形,第四个图形不是中心对称图形.
故中心对称图形有3个.
故选:B.
4.直角三角形两直角边长为5和12,则此直角三角形斜边上的中线的长是( )
A.5 B.6 C.6.5 D.13
解:由题意得,斜边=,所以斜边上的中线=×13=6.5.
故选:C.
5.一个人做“抛硬币”的游戏,正面出现4次,反面出现了6次,正确说法为( )
A.出现正面的频率是4 B.出现反面的频率是6
C.出现反面的频率是60% D.出现正面的频数是40%
解:A、应为:出现正面的频数是4;
B、应为:出现反面的频数是6;
C、正确;
D、计算错误.
故选:C.
6.在平面直角坐标系中,将直线l1:y=3x平移后得到直线l2:y=3x+2,则下列平移的做法正确的是( )
A.将l1向左平移2个单位 B.将l1向右平移2个单位
C.将l1向上平移2个单位 D.将l1向下平移2个单位
解:将直线l1:y=3x向上平移2个单位得到直线l2:y=3x+2.
故选:C.
7.关于函数y=﹣2x+1,下列结论正确的是( )
A.图象必经过(﹣2,1)
B.y随x的增大而增大
C.图象经过第一、二、三象限
D.当x>时,y<0
解:根据一次函数的性质,依次分析可得,
A、x=﹣2时,y=﹣2×﹣2+1=5,故图象必经过(﹣2,5),故错误,
B、k<0,则y随x的增大而减小,故错误,
C、k=﹣2<0,b=1>0,则图象经过第一、二、四象限,故错误,
D、当x>时,y<0,正确;
故选:D.
8.下列说法错误的是( )
A.△ABC中,若有∠A+∠B=∠C,则△ABC是直角三角形
B.△ABC中,若有∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
C.△ABC的三边长分别为:a,b,c,且a2﹣b2=c2,则△ABC是直角三角形
D.在一个直角三角形中,有两边的长度分别是3和5,则第三边的长度是4
解:A、△ABC中,若有∠A+∠B=∠C,则∠C=90°,∴△ABC是直角三角形,说法正确;
B、△ABC中,若有∠A:∠B:∠C=1:2:3,则∠C=90°,∴△ABC是直角三角形,说法正确;
C、△ABC的三边长分别为:a,b,c,且a2﹣b2=c2,则a2=b2+c2,∴△ABC是直角三角形,说法正确;
D、在一个直角三角形中,有两边的长度分别是3和5,则第三边的长度是4或,说法错误;
故选:D.
9.如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:①△ODC是等边三角形;②BC=2AB:③S△AOE=S△COE,其中正确结论有( )
A.0个 B.1个 C.2个 D.3个
解:∵四边形ABCD是矩形,
∴AD∥BC,∠BAD=∠ABC=∠ADC=90°,OA=OC,OD=OB,AC=BD,
∴OA=OD=OC=OB,
∵AE平分∠BAD,
∴∠DAE=45°,
∵∠CAE=15°,
∴∠DAC=45°﹣15°=30°,
∴∠ACD=90°﹣∠DAC=90°﹣30°=60°,
∵OD=OC,
∴△ODC是等边三角形,故①正确;
∵AD∥BC,
∴∠ACB=∠DAC=30°,
∵∠ABC=90°,
∴AC=2AB,
∴2AB>BC,故②错误;
∵OA=OC,
∴S△AOE=S△COE,故③正确;
正确的结论有2个,
故选:C.
10.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象,有以下结论:①m=1;②a=40;③甲车从A地到B地共用了6.5小时;④当两车相距50km时,乙车用时为h.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
解:由题意,得m=1.5﹣0.5=1,故①结论正确;
120÷(3.5﹣0.5)=40(km/h),则a=40,故②结论正确;
设甲车休息之后行驶路程y(km)与时间x(h)的函数关系式为y=kx+b,由题意,得:
,
解得,
∴y=40x﹣20(1.5<x≤7),
当y=260时,260=40x﹣20,
解得:x=7,
∴甲车从A地到B地共用了7小时,故③结论错误;
当1.5<x≤7时,y=40x﹣20.
设乙车行驶的路程y与时间x之间的解析式为y=k'x+b',由题意得:
,
解得,
∴y=80x﹣160.
当40x﹣20﹣50=80x﹣160时,
解得:x=,
当40x﹣20+50=80x﹣160时,
解得:x=,
∴﹣2=,﹣2=,
所以乙车行驶小时或小时,两车恰好相距50km,故④结论错误.
∴正确结论的个数是2个.
故选:B.
二、填空题(共8小题,每小題3分,共24分)
11.一个多边形的内角和跟它的外角和相等,则这个多边形是 4 边形.
解:设多边形的边数为n,根据题意
(n﹣2)?180°=360°,
解得n=4.
故答案为:4.
12.菱形的周长是20,一条对角线的长为6,则它的面积为 24 .
解:∵菱形的周长是20
∴边长=5
∵一条对角线的长为6
∴另一条对角线的长为8
∴菱形的面积=×6×8=24.
故答案为24.
13.已知一次函数y=(m+2)x+1,函数y的值随x值的增大而减小,则常数m的取值可以是 ﹣3(答案不唯一) .(只需要写一个满足条件的常数m)
解:∵一次函数y=(m+2)x+1,函数y的值随x值的增大而减小,
∴m+2<0
∴m<﹣2,
∴m的值可以是﹣3,
故答案为﹣3(答案不唯一).
14.如图是某市晚报记者在抽样调查了一些市民用于读书、读报、参加“全民健身运动”等休闲娱乐活动的时间后,绘制的频率分布直方图(共六组),已知从左往右前五组的频率之和为0.94,如果第六组有12个数,则此次抽样的样本容量是 200 .
解:根据频数分布直方图中每一组内的频率总和等于1,
可知第六组的频率为1﹣0.94=0.06,
又因为第六组有12个数,
所以此次抽样的样本容量是12÷0.06=200;
故答案为200.
15.如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是 3 .
解:过点D作DE⊥BC于E,则DE为点D到BC的距离,
在Rt△ABD中,∠A=90°,AB=4,BD=5,
由勾股定理得:AD===3,
∵BD平分∠ABC,∠A=90°,DE⊥BC,
∴DE=AD=3,
故答案为:3.
16.如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“卒”的坐标分别是(3,0)和(﹣2,﹣1),那么“兵”的坐标为 (﹣3,2) .
解:如图所示:“兵”的坐标为(﹣3,2).
故答案为:(﹣3,2).
17.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为 5 .
解:设DE=x,则AE=8﹣x.
根据折叠的性质,得∠EBD=∠CBD.
∵AD∥BC,
∴∠CBD=∠ADB,
∴∠EBD=∠EDB,
∴BE=DE=x.
在直角三角形ABE中,根据勾股定理,得
x2=(8﹣x)2+16,
解得x=5.
故答案为:5.
18.如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 (﹣1,2) .
解:∵直线y=2x+4与y轴交于B点,
∴x=0时,
得y=4,
∴B(0,4).
∵以OB为边在y轴右侧作等边三角形OBC,
∴C在线段OB的垂直平分线上,
∴C点纵坐标为2.
将y=2代入y=2x+4,得2=2x+4,
解得x=﹣1.
故答案为:(﹣1,2).
三、解答题(本大题共8小題,66分。其中:第19至25小題各8分:第26小题10分)
19.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,AC=6,BD=9,CD=5,试求△COD的周长.
解:∵平行四边形ABCD的对角线AC与BD相交于点O,AC=6,BD=9,
∴DO=BD=×9=4.5,CO=AC=×6=3,
又∵CD=5,
∴△COD的周长=DO+CO+CD=4.5+3+5=12.5.
20.如图,在平面直角坐标系中,O是坐标原点,A,B坐标分别为(2,0),(﹣1,3).
(1)直接写出点B关于y轴的对称点的坐标: (1,3) .
(2)请用直尺在方格中画出△O′A′B′,要求:△O′A′B′和△OAB关于点(﹣1,0)成中心对称.(保留作图痕迹,不写作法)
解:(1)点B关于y轴的对称点的坐标为(1,3);
故答案为(1,3);
(2)如图,△O′A′B′为所作.
21.垃圾分类是一项“利国利民”的民生工程,需要全社会的共同参与.某校积极参与垃圾分类活动,以班级为单位收集可回收垃圾,如图表是七年级各班一周收集的可回收垃圾的重量(千克)的频数表和频数分布直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的重量的频数表
组别(kg) 频数
4.0~4.5 2
4.5~5.0 a
5.0~5.5 3
5.5~6.0 1
(1)求a的值
(2)已知收集的可回收垃圾以1.1元/kg被回收,该年级这周收集的可回收垃圾被回收后所得金额能否达到60元?
解:(1)由频数分布直方图可知4.5~5.0的频数a=4;
(2)∵该年级这周收集的可回收垃圾的质量小于4.5×2+5.0×4+5.5×3+6.0=51.5(kg),
∴该年级这周收集的可回收垃圾被回收后所得金额小于51.5×1.1=56.65(元),
∴该年级这周收集的可回收垃圾被回收后所得金额不能达到60元.
22.如图,在树上距地面10m的D处有两只猴子,它们同时发现地面上C处有一筐水果,一只猴子从D处向上爬到树顶A处,然后利用拉在A处的滑绳AC滑到C处,另一只猴子从D处先滑到地面B,再由B跑到C,已知两猴子所经过的路程都是15m,求树高AB.
解:Rt△ABC中,∠B=90°,
设BC=a(m),AC=b(m),AD=x(m)
则10+a=x+b=15(m).
∴a=5(m),b=15﹣x(m)
又在Rt△ABC中,由勾股定理得:(10+x)2+a2=b2,
∴(10+x)2+52=(15﹣x)2,
解得,x=2,即AD=2(米)
∴AB=AD+DB=2+10=12(米)
答:树高AB为12米.
23.如图,一次函数y=kx+b的图象经过(2,4)、(0,2)两点,与x轴相交于点C.求:
(1)此一次函数的解析式;
(2)△AOC的面积.
解:(1)∵由图可知A(2,4)、B(0,2),
,
解得,
故此一次函数的解析式为:y=x+2;
(2)∵由图可知,C(﹣2,0),A(2,4),
∴OC=2,AD=4,
∴S△AOC=OC?AD=×2×4=4.
答:△AOC的面积是4.
24.如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵∠OBC=∠OCB,
∴OB=OC,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)解:AB=AD(或AC⊥BD答案不唯一).
理由:∵四边形ABCD是矩形,
又∵AB=AD,
∴四边形ABCD是正方形.
或:∵四边形ABCD是矩形,
又∵AC⊥BD,
∴四边形ABCD是正方形.
25.某水果店以每千克8元的价格购进苹果若干千克,销售了部分苹果后,余下的苹果每千克降价4元销售,全部售完.销售金额y(元)与销售量x(千克)之间的关系如图所示,请根据图象提供的信息完成下列问题:
(1)降价前苹果的销售单价是 16 元/千克;
(2)求降价后销售金额y(元)与销售量x(千克)之间的函数解析式,并写出自变量的取值范围;
(3)该水果店这次销售苹果盈利了多少元?
解:(1)由图可得,
降价前苹果的销售单价是:640÷40=16(元/千克),
故答案为:16;
(2)降价后销售的苹果千克数是:(760﹣640)÷(16﹣4)=10(千克).
∴销售的苹果总数为40+10=50(千克).
设降价后销售金额y(元)与销售量x(千克)之间的函数解析式是y=kx+b,
∵该函数过点(40,640),(50,760),
∴,
解得:.
即降价后销售金额y(元)与销售量x(千克)之间的函数解析式是y=12x+160(40<x≤50);
(3)该水果店这次销售苹果盈利了:760﹣8×50=360(元).
答:该水果店这次销售苹果盈利了360元.
26.某校八年级数学学习小组在探究学习的过程中,用两块完全相同的且含60°角(∠ABC=∠AFE=60°)的直角三角板ABC与AFE按①所示的方式放置.现将Rt△AEF绕直角顶点A按逆时针方向旋转∠a(0°<α<90°),如图②,AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角∠α=30°时,四边形ABPF是什么样的特殊四边形?说明理由.
解:(1)由旋转可知∠BAM=∠FAN=α,
又由已知可得∠B=∠F=60°,AB=AF,
在△ABM和△AFN中,
,
∴△ABM≌△AFN(ASA),
∴AM=AN.
(2)四边形ABPF是菱形,理由如下:
当旋转角∠α=30°时,
∵∠B=∠F=60°,
∴∠AMB=∠ANF=90°,
∵∠FAE=∠BAC=90°,
∴∠AMB=∠FAE,∠ANF=∠BAC,
则AF∥BP,AB∥PF,
∴四边形ABPF为平行四边形,
又AB=AF,
∴四边形ABPF为菱形.
一、选择题(共10小题,共30分).
1.在平面直角坐标系中,点(2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.五边形的内角和是( )
A.180° B.360° C.540° D.720°
3.下列图形中,是中心对称图形的有( )
A.4个 B.3个 C.2个 D.1个
4.直角三角形两直角边长为5和12,则此直角三角形斜边上的中线的长是( )
A.5 B.6 C.6.5 D.13
5.一个人做“抛硬币”的游戏,正面出现4次,反面出现了6次,正确说法为( )
A.出现正面的频率是4 B.出现反面的频率是6
C.出现反面的频率是60% D.出现正面的频数是40%
6.在平面直角坐标系中,将直线l1:y=3x平移后得到直线l2:y=3x+2,则下列平移的做法正确的是( )
A.将l1向左平移2个单位 B.将l1向右平移2个单位
C.将l1向上平移2个单位 D.将l1向下平移2个单位
7.关于函数y=﹣2x+1,下列结论正确的是( )
A.图象必经过(﹣2,1)
B.y随x的增大而增大
C.图象经过第一、二、三象限
D.当x>时,y<0
8.下列说法错误的是( )
A.△ABC中,若有∠A+∠B=∠C,则△ABC是直角三角形
B.△ABC中,若有∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
C.△ABC的三边长分别为:a,b,c,且a2﹣b2=c2,则△ABC是直角三角形
D.在一个直角三角形中,有两边的长度分别是3和5,则第三边的长度是4
9.如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:①△ODC是等边三角形;②BC=2AB:③S△AOE=S△COE,其中正确结论有( )
A.0个 B.1个 C.2个 D.3个
10.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象,有以下结论:①m=1;②a=40;③甲车从A地到B地共用了6.5小时;④当两车相距50km时,乙车用时为h.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(共8小题,每小題3分,共24分)
11.一个多边形的内角和跟它的外角和相等,则这个多边形是 边形.
12.菱形的周长是20,一条对角线的长为6,则它的面积为 .
13.已知一次函数y=(m+2)x+1,函数y的值随x值的增大而减小,则常数m的取值可以是 .(只需要写一个满足条件的常数m)
14.如图是某市晚报记者在抽样调查了一些市民用于读书、读报、参加“全民健身运动”等休闲娱乐活动的时间后,绘制的频率分布直方图(共六组),已知从左往右前五组的频率之和为0.94,如果第六组有12个数,则此次抽样的样本容量是 .
15.如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是 .
16.如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“卒”的坐标分别是(3,0)和(﹣2,﹣1),那么“兵”的坐标为 .
17.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为 .
18.如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 .
三、解答题(本大题共8小題,66分。其中:第19至25小題各8分:第26小题10分)
19.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,AC=6,BD=9,CD=5,试求△COD的周长.
20.如图,在平面直角坐标系中,O是坐标原点,A,B坐标分别为(2,0),(﹣1,3).
(1)直接写出点B关于y轴的对称点的坐标: .
(2)请用直尺在方格中画出△O′A′B′,要求:△O′A′B′和△OAB关于点(﹣1,0)成中心对称.(保留作图痕迹,不写作法)
21.垃圾分类是一项“利国利民”的民生工程,需要全社会的共同参与.某校积极参与垃圾分类活动,以班级为单位收集可回收垃圾,如图表是七年级各班一周收集的可回收垃圾的重量(千克)的频数表和频数分布直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的重量的频数表
组别(kg) 频数
4.0~4.5 2
4.5~5.0 a
5.0~5.5 3
5.5~6.0 1
(1)求a的值
(2)已知收集的可回收垃圾以1.1元/kg被回收,该年级这周收集的可回收垃圾被回收后所得金额能否达到60元?
22.如图,在树上距地面10m的D处有两只猴子,它们同时发现地面上C处有一筐水果,一只猴子从D处向上爬到树顶A处,然后利用拉在A处的滑绳AC滑到C处,另一只猴子从D处先滑到地面B,再由B跑到C,已知两猴子所经过的路程都是15m,求树高AB.
23.如图,一次函数y=kx+b的图象经过(2,4)、(0,2)两点,与x轴相交于点C.求:
(1)此一次函数的解析式;
(2)△AOC的面积.
24.如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.
25.某水果店以每千克8元的价格购进苹果若干千克,销售了部分苹果后,余下的苹果每千克降价4元销售,全部售完.销售金额y(元)与销售量x(千克)之间的关系如图所示,请根据图象提供的信息完成下列问题:
(1)降价前苹果的销售单价是 元/千克;
(2)求降价后销售金额y(元)与销售量x(千克)之间的函数解析式,并写出自变量的取值范围;
(3)该水果店这次销售苹果盈利了多少元?
26.某校八年级数学学习小组在探究学习的过程中,用两块完全相同的且含60°角(∠ABC=∠AFE=60°)的直角三角板ABC与AFE按①所示的方式放置.现将Rt△AEF绕直角顶点A按逆时针方向旋转∠a(0°<α<90°),如图②,AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角∠α=30°时,四边形ABPF是什么样的特殊四边形?说明理由.
参考答案
一、选择题(共10小题,每小题3分,共30分)请将正确答案序号填写在答题卡上
1.在平面直角坐标系中,点(2,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:在平面直角坐标系中,点(2,1)的横坐标和纵坐标都大于0,所以点(2,1)在第一象限.
故选:A.
2.五边形的内角和是( )
A.180° B.360° C.540° D.720°
解:五边形的内角和是:
(5﹣2)×180°
=3×180°
=540°
故选:C.
3.下列图形中,是中心对称图形的有( )
A.4个 B.3个 C.2个 D.1个
解:从左到右,第一、第二、第三个图形是中心对称图形,第四个图形不是中心对称图形.
故中心对称图形有3个.
故选:B.
4.直角三角形两直角边长为5和12,则此直角三角形斜边上的中线的长是( )
A.5 B.6 C.6.5 D.13
解:由题意得,斜边=,所以斜边上的中线=×13=6.5.
故选:C.
5.一个人做“抛硬币”的游戏,正面出现4次,反面出现了6次,正确说法为( )
A.出现正面的频率是4 B.出现反面的频率是6
C.出现反面的频率是60% D.出现正面的频数是40%
解:A、应为:出现正面的频数是4;
B、应为:出现反面的频数是6;
C、正确;
D、计算错误.
故选:C.
6.在平面直角坐标系中,将直线l1:y=3x平移后得到直线l2:y=3x+2,则下列平移的做法正确的是( )
A.将l1向左平移2个单位 B.将l1向右平移2个单位
C.将l1向上平移2个单位 D.将l1向下平移2个单位
解:将直线l1:y=3x向上平移2个单位得到直线l2:y=3x+2.
故选:C.
7.关于函数y=﹣2x+1,下列结论正确的是( )
A.图象必经过(﹣2,1)
B.y随x的增大而增大
C.图象经过第一、二、三象限
D.当x>时,y<0
解:根据一次函数的性质,依次分析可得,
A、x=﹣2时,y=﹣2×﹣2+1=5,故图象必经过(﹣2,5),故错误,
B、k<0,则y随x的增大而减小,故错误,
C、k=﹣2<0,b=1>0,则图象经过第一、二、四象限,故错误,
D、当x>时,y<0,正确;
故选:D.
8.下列说法错误的是( )
A.△ABC中,若有∠A+∠B=∠C,则△ABC是直角三角形
B.△ABC中,若有∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
C.△ABC的三边长分别为:a,b,c,且a2﹣b2=c2,则△ABC是直角三角形
D.在一个直角三角形中,有两边的长度分别是3和5,则第三边的长度是4
解:A、△ABC中,若有∠A+∠B=∠C,则∠C=90°,∴△ABC是直角三角形,说法正确;
B、△ABC中,若有∠A:∠B:∠C=1:2:3,则∠C=90°,∴△ABC是直角三角形,说法正确;
C、△ABC的三边长分别为:a,b,c,且a2﹣b2=c2,则a2=b2+c2,∴△ABC是直角三角形,说法正确;
D、在一个直角三角形中,有两边的长度分别是3和5,则第三边的长度是4或,说法错误;
故选:D.
9.如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:①△ODC是等边三角形;②BC=2AB:③S△AOE=S△COE,其中正确结论有( )
A.0个 B.1个 C.2个 D.3个
解:∵四边形ABCD是矩形,
∴AD∥BC,∠BAD=∠ABC=∠ADC=90°,OA=OC,OD=OB,AC=BD,
∴OA=OD=OC=OB,
∵AE平分∠BAD,
∴∠DAE=45°,
∵∠CAE=15°,
∴∠DAC=45°﹣15°=30°,
∴∠ACD=90°﹣∠DAC=90°﹣30°=60°,
∵OD=OC,
∴△ODC是等边三角形,故①正确;
∵AD∥BC,
∴∠ACB=∠DAC=30°,
∵∠ABC=90°,
∴AC=2AB,
∴2AB>BC,故②错误;
∵OA=OC,
∴S△AOE=S△COE,故③正确;
正确的结论有2个,
故选:C.
10.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲、乙两车行驶的距离y(km)与时间x(h)的函数图象,有以下结论:①m=1;②a=40;③甲车从A地到B地共用了6.5小时;④当两车相距50km时,乙车用时为h.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
解:由题意,得m=1.5﹣0.5=1,故①结论正确;
120÷(3.5﹣0.5)=40(km/h),则a=40,故②结论正确;
设甲车休息之后行驶路程y(km)与时间x(h)的函数关系式为y=kx+b,由题意,得:
,
解得,
∴y=40x﹣20(1.5<x≤7),
当y=260时,260=40x﹣20,
解得:x=7,
∴甲车从A地到B地共用了7小时,故③结论错误;
当1.5<x≤7时,y=40x﹣20.
设乙车行驶的路程y与时间x之间的解析式为y=k'x+b',由题意得:
,
解得,
∴y=80x﹣160.
当40x﹣20﹣50=80x﹣160时,
解得:x=,
当40x﹣20+50=80x﹣160时,
解得:x=,
∴﹣2=,﹣2=,
所以乙车行驶小时或小时,两车恰好相距50km,故④结论错误.
∴正确结论的个数是2个.
故选:B.
二、填空题(共8小题,每小題3分,共24分)
11.一个多边形的内角和跟它的外角和相等,则这个多边形是 4 边形.
解:设多边形的边数为n,根据题意
(n﹣2)?180°=360°,
解得n=4.
故答案为:4.
12.菱形的周长是20,一条对角线的长为6,则它的面积为 24 .
解:∵菱形的周长是20
∴边长=5
∵一条对角线的长为6
∴另一条对角线的长为8
∴菱形的面积=×6×8=24.
故答案为24.
13.已知一次函数y=(m+2)x+1,函数y的值随x值的增大而减小,则常数m的取值可以是 ﹣3(答案不唯一) .(只需要写一个满足条件的常数m)
解:∵一次函数y=(m+2)x+1,函数y的值随x值的增大而减小,
∴m+2<0
∴m<﹣2,
∴m的值可以是﹣3,
故答案为﹣3(答案不唯一).
14.如图是某市晚报记者在抽样调查了一些市民用于读书、读报、参加“全民健身运动”等休闲娱乐活动的时间后,绘制的频率分布直方图(共六组),已知从左往右前五组的频率之和为0.94,如果第六组有12个数,则此次抽样的样本容量是 200 .
解:根据频数分布直方图中每一组内的频率总和等于1,
可知第六组的频率为1﹣0.94=0.06,
又因为第六组有12个数,
所以此次抽样的样本容量是12÷0.06=200;
故答案为200.
15.如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是 3 .
解:过点D作DE⊥BC于E,则DE为点D到BC的距离,
在Rt△ABD中,∠A=90°,AB=4,BD=5,
由勾股定理得:AD===3,
∵BD平分∠ABC,∠A=90°,DE⊥BC,
∴DE=AD=3,
故答案为:3.
16.如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“卒”的坐标分别是(3,0)和(﹣2,﹣1),那么“兵”的坐标为 (﹣3,2) .
解:如图所示:“兵”的坐标为(﹣3,2).
故答案为:(﹣3,2).
17.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为 5 .
解:设DE=x,则AE=8﹣x.
根据折叠的性质,得∠EBD=∠CBD.
∵AD∥BC,
∴∠CBD=∠ADB,
∴∠EBD=∠EDB,
∴BE=DE=x.
在直角三角形ABE中,根据勾股定理,得
x2=(8﹣x)2+16,
解得x=5.
故答案为:5.
18.如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C′恰好落在直线AB上,则点C′的坐标为 (﹣1,2) .
解:∵直线y=2x+4与y轴交于B点,
∴x=0时,
得y=4,
∴B(0,4).
∵以OB为边在y轴右侧作等边三角形OBC,
∴C在线段OB的垂直平分线上,
∴C点纵坐标为2.
将y=2代入y=2x+4,得2=2x+4,
解得x=﹣1.
故答案为:(﹣1,2).
三、解答题(本大题共8小題,66分。其中:第19至25小題各8分:第26小题10分)
19.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,AC=6,BD=9,CD=5,试求△COD的周长.
解:∵平行四边形ABCD的对角线AC与BD相交于点O,AC=6,BD=9,
∴DO=BD=×9=4.5,CO=AC=×6=3,
又∵CD=5,
∴△COD的周长=DO+CO+CD=4.5+3+5=12.5.
20.如图,在平面直角坐标系中,O是坐标原点,A,B坐标分别为(2,0),(﹣1,3).
(1)直接写出点B关于y轴的对称点的坐标: (1,3) .
(2)请用直尺在方格中画出△O′A′B′,要求:△O′A′B′和△OAB关于点(﹣1,0)成中心对称.(保留作图痕迹,不写作法)
解:(1)点B关于y轴的对称点的坐标为(1,3);
故答案为(1,3);
(2)如图,△O′A′B′为所作.
21.垃圾分类是一项“利国利民”的民生工程,需要全社会的共同参与.某校积极参与垃圾分类活动,以班级为单位收集可回收垃圾,如图表是七年级各班一周收集的可回收垃圾的重量(千克)的频数表和频数分布直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的重量的频数表
组别(kg) 频数
4.0~4.5 2
4.5~5.0 a
5.0~5.5 3
5.5~6.0 1
(1)求a的值
(2)已知收集的可回收垃圾以1.1元/kg被回收,该年级这周收集的可回收垃圾被回收后所得金额能否达到60元?
解:(1)由频数分布直方图可知4.5~5.0的频数a=4;
(2)∵该年级这周收集的可回收垃圾的质量小于4.5×2+5.0×4+5.5×3+6.0=51.5(kg),
∴该年级这周收集的可回收垃圾被回收后所得金额小于51.5×1.1=56.65(元),
∴该年级这周收集的可回收垃圾被回收后所得金额不能达到60元.
22.如图,在树上距地面10m的D处有两只猴子,它们同时发现地面上C处有一筐水果,一只猴子从D处向上爬到树顶A处,然后利用拉在A处的滑绳AC滑到C处,另一只猴子从D处先滑到地面B,再由B跑到C,已知两猴子所经过的路程都是15m,求树高AB.
解:Rt△ABC中,∠B=90°,
设BC=a(m),AC=b(m),AD=x(m)
则10+a=x+b=15(m).
∴a=5(m),b=15﹣x(m)
又在Rt△ABC中,由勾股定理得:(10+x)2+a2=b2,
∴(10+x)2+52=(15﹣x)2,
解得,x=2,即AD=2(米)
∴AB=AD+DB=2+10=12(米)
答:树高AB为12米.
23.如图,一次函数y=kx+b的图象经过(2,4)、(0,2)两点,与x轴相交于点C.求:
(1)此一次函数的解析式;
(2)△AOC的面积.
解:(1)∵由图可知A(2,4)、B(0,2),
,
解得,
故此一次函数的解析式为:y=x+2;
(2)∵由图可知,C(﹣2,0),A(2,4),
∴OC=2,AD=4,
∴S△AOC=OC?AD=×2×4=4.
答:△AOC的面积是4.
24.如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵∠OBC=∠OCB,
∴OB=OC,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)解:AB=AD(或AC⊥BD答案不唯一).
理由:∵四边形ABCD是矩形,
又∵AB=AD,
∴四边形ABCD是正方形.
或:∵四边形ABCD是矩形,
又∵AC⊥BD,
∴四边形ABCD是正方形.
25.某水果店以每千克8元的价格购进苹果若干千克,销售了部分苹果后,余下的苹果每千克降价4元销售,全部售完.销售金额y(元)与销售量x(千克)之间的关系如图所示,请根据图象提供的信息完成下列问题:
(1)降价前苹果的销售单价是 16 元/千克;
(2)求降价后销售金额y(元)与销售量x(千克)之间的函数解析式,并写出自变量的取值范围;
(3)该水果店这次销售苹果盈利了多少元?
解:(1)由图可得,
降价前苹果的销售单价是:640÷40=16(元/千克),
故答案为:16;
(2)降价后销售的苹果千克数是:(760﹣640)÷(16﹣4)=10(千克).
∴销售的苹果总数为40+10=50(千克).
设降价后销售金额y(元)与销售量x(千克)之间的函数解析式是y=kx+b,
∵该函数过点(40,640),(50,760),
∴,
解得:.
即降价后销售金额y(元)与销售量x(千克)之间的函数解析式是y=12x+160(40<x≤50);
(3)该水果店这次销售苹果盈利了:760﹣8×50=360(元).
答:该水果店这次销售苹果盈利了360元.
26.某校八年级数学学习小组在探究学习的过程中,用两块完全相同的且含60°角(∠ABC=∠AFE=60°)的直角三角板ABC与AFE按①所示的方式放置.现将Rt△AEF绕直角顶点A按逆时针方向旋转∠a(0°<α<90°),如图②,AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角∠α=30°时,四边形ABPF是什么样的特殊四边形?说明理由.
解:(1)由旋转可知∠BAM=∠FAN=α,
又由已知可得∠B=∠F=60°,AB=AF,
在△ABM和△AFN中,
,
∴△ABM≌△AFN(ASA),
∴AM=AN.
(2)四边形ABPF是菱形,理由如下:
当旋转角∠α=30°时,
∵∠B=∠F=60°,
∴∠AMB=∠ANF=90°,
∵∠FAE=∠BAC=90°,
∴∠AMB=∠FAE,∠ANF=∠BAC,
则AF∥BP,AB∥PF,
∴四边形ABPF为平行四边形,
又AB=AF,
∴四边形ABPF为菱形.
同课章节目录
