七年级数学不等式的性质课件
文档属性
| 名称 | 七年级数学不等式的性质课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 1012.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-19 00:00:00 | ||
图片预览










文档简介
(共43张PPT)
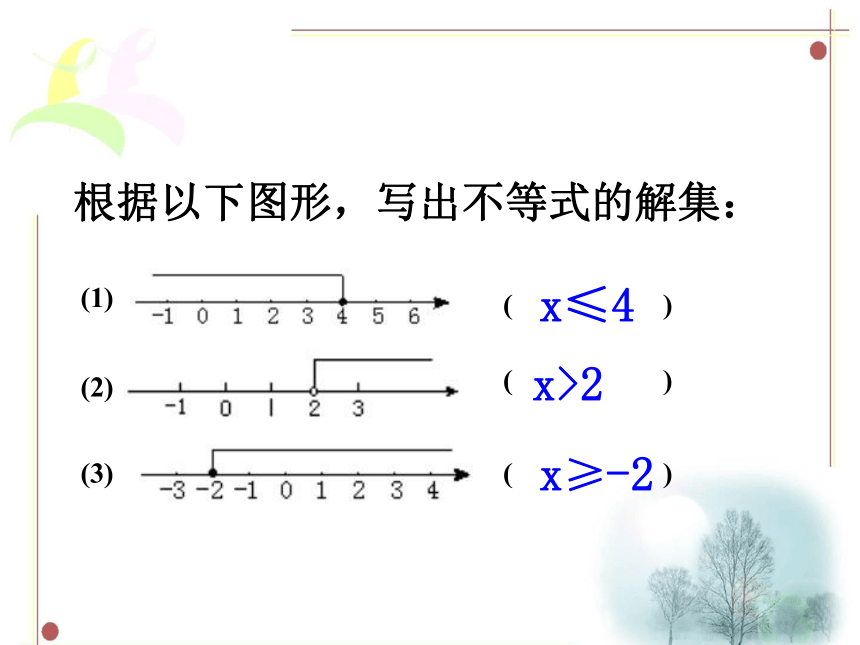
根据以下图形,写出不等式的解集:
(1)
( )
(2)
( )
(3)
( )
x≤4
x>2
x≥-2
大于向右,小于向左,有等号为实心,无等号为空心.
(1)x≤-1 (2)x≥-3
(3)x<2 (4)-3≤x<2
在数轴上表示下列不等式的解集:
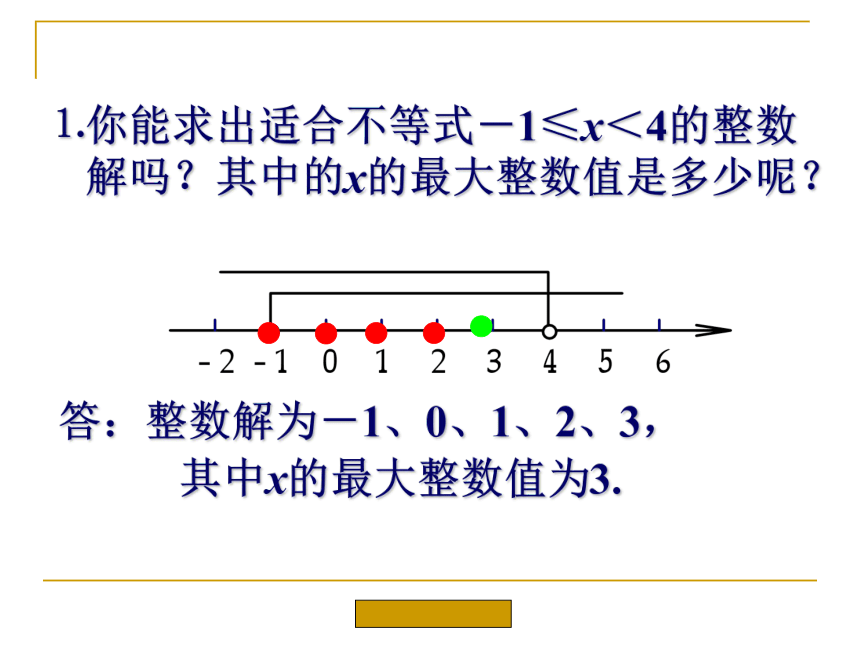
答:整数解为-1、0、1、2、3,
其中x的最大整数值为3.
⒈你能求出适合不等式-1≤x<4的整数
解吗?其中的x的最大整数值是多少呢?
复习回顾
一.等式的性质
等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.
如果a=b,那么a±c=b±c
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
如果a=b,那么ac=bc或 (c≠0),
不等式是否具有类似的性质呢?
如果 5 > 3
那么 5+2 ____ 3+2 , 5 -2____3-2
>
>
如果-1< 3,
那么-1+2____3+2, -1- 3____3 - 3
<
<
性质1 :如果 a>b, 那么 a+c>b+c 或 a-c>b-c
即:不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
6÷5 ____ 2÷ 5 ,
6 ÷ (-5)____2÷ (-5)
不等式两边都乘以(或除以)同一个不为零的数,不等号的方向是否改变?
如果 6 >2
那么 6×5 ____ 2× 5 ,
6 ×(-5)____2×(-5),
>
如果-2< 3,
那么-2×6____3×6,
-2×(- 6)____3×( - 6),
-2÷2____3÷2,
-2÷ (- 4)____3÷ ( - 4)
>
>
<
<
<
<
>
发现:同乘以一个正数,不等号方向不变,同乘以一个 负数不等号方向改变,同乘以0的时候相等.
<
>
>
>
<
<
=
猜想2:不等式两边都乘以(或除以)同一个不为零的数,不等号
的方向是否改变?
正数:7×3 4×3 负数:7×(-1) 4 × (-1)
7×2 4×2 7 ×(-2) 4 × (-2)
7×1 4×1 7 × (-3) 4 × (-3)
零: 7×0 4×0
将不等式 7>4 的两边都乘以同一个数,比较所得结果的大小,
用 >、< 、= 填空
举例分析:
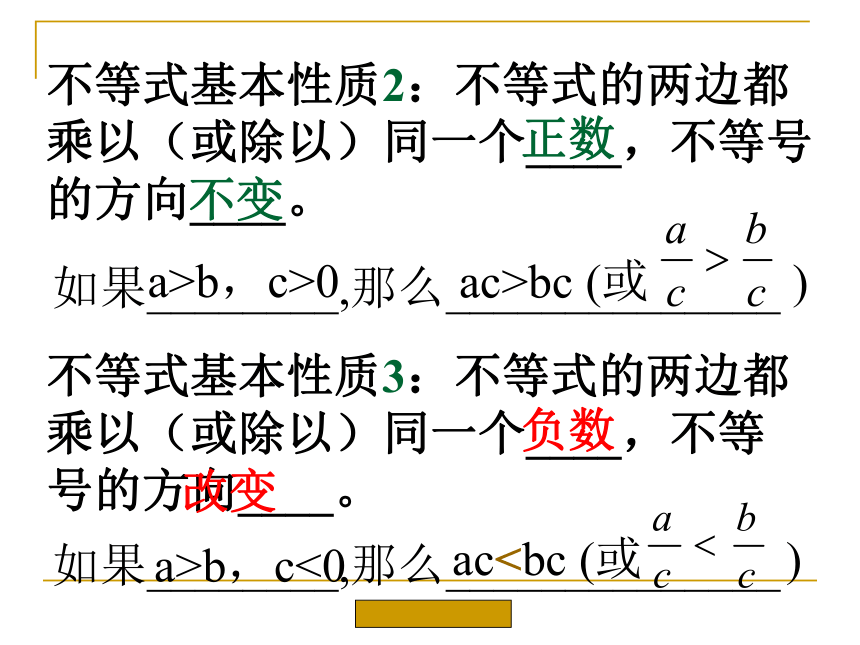
不等式基本性质2:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
不等式基本性质3:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
如果________,那么______________
不变
正数
a>b,c>0
ac>bc (或 )
负数
改变
如果________,那么______________
a>b,c<0
ac例1:
判断下列各题的推导是否正确?为什么(学生口答)
(1)因为7.5>5.7,所以-7.5<-5.7;
(2)因为a+8>4,所以a>-4;
(3)因为4a>4b,所以a>b;
(4)因为-1>-2,所以-a-1>-a-2;
(5)因为3>2,所以3a>2a.
答:
.
(1)正确,根据不等式基本性质3.
(2)正确,根据不等式基本性质1.
(3)正确,根据不等式基本性质2.
(4)正确,根据不等式基本性质1.
(5)不对,应分情况逐一讨论.
当a>0时,3a>2a.(不等式基本性质2)
当 a=0时,3a=2a.
当a<0时,3a<2a.(不等式基本性质3)
我是最棒的
选择适当的不等号填空:
(1)∵0 1,
∴ a a+1(不等式的基本性质1);
(2)∵(a-1)2 0,
∴(a-1)2-2 -2(不等式的基本性质1)
(3)若x+1>0,两边同加上-1,得____________
(依据:_____________________).
(4)若2 x >-6,两边同除以2,得________,依据_______________.
(5)若-0.5 x≤1,两边同乘以-2,得________,依据___________
<
<
≥
≥
x >-1
不等式的基本性质1
x >-3
不等式的基本性质2
X≥-2
不等式的基本性质3
试一试
1.若-m>5,则m -5.
2.如果x/y>0, 那么xy 0.
3.如果a>-1,那么a-b -1-b.
4.-0.9<-0.3,两边都除以(-0.3),得_______.
>
>
<
3 >1
例 已知a<0 ,试比较2a与a的大小。
解法一:∵2>1,a<0,
∴2a<a(不等式的基本性质3)
解法二: 在数轴上分别表示2a和a的点(a<0),如图.2a位于a的左边,所以2a<a
0
a
2a
∣a∣
∣a∣
想一想:还有其他比较2a与a的大小的方法吗?
∵ 2a-a=a, 又∵ a<0,
∴ 2a-a<0,
∴2a不等式的基本性质
(1)不等式的两边都加上(或减去)同一个数或同一个式子,不等号的方向不变.
(2) 不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
(3) 不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
知 识 回 顾
解:(1) x-2+2<3+2
x<5
(2) 6x-5x<5x-1-5x
x<-1
例1.根据不等式的基本性质,把下列不等式化成
x<a 或x>a的形式:
x-2< 3 (2) 6x< 5x-1
:解不等式:
(1)x-7<8 (2)3x<2x-3
这两小题中不等式的变形与方程的什么变形相类似?
解:
解:
x-7+7 <8+7
3x-2x <2x-3-2x
移
移
x <8+7
x <15
3x-2x <-3
x <-3
这里的变形与方程中的移项相类似:
注意:移项要变号
例题解析
这两小题中不等式的变形与方程的什么变形相类似?有什么不同?
解(1)
(2)
与解方程一样,
解不等式的过程,
就是要将不等式
变形成x>a或x的形式。
不等式两边同乘以负数要改变不等号的方向
学习离不开总结!
通过今天的探讨学习,你获得了哪些新知识 大胆说出来,和大家交流一下!
1、解一元一次不等式的依据
如果a>b,那么a+c>b+c,a-c>b-c
如果a>b,并且c>0,那么ac>bc。
如果a>b,并且c<0,那么ac不等式的性质
2、解一元一次不等式的步骤与解一元一次方程的异同点
不等式两边同乘以负数要改变不等号的方向
解一元一次不等式的基本步骤:
(1);移项;
(2)合并同类项;
(3)化系数为1.
解下列不等式,并在数轴上表示出来:
1、X-2>0 2、X+1>0
3、-2x<4 4、3x+3≤0
解:x >2
-3
-2
-1
0
4
2
1
3
5
。
x >-1
-3
-2
-1
0
4
2
1
3
5
x >-2
-3
-2
-1
0
4
2
1
3
5
。
x ≤-1
-3
-2
-1
0
4
2
1
3
5
.
。
试一试,可要仔细呦!
求不等式1-2x < 6的负整数解
发挥集体的智慧,让我们共同努力
思考:要知道x的负整数解,首先应该求出一元一次此不等式x的解集.
要使x的解是负整数,则x还必须小于0
所以不等式的负整数解为 -2 、-1
1-2x < 6
不等式x< 的正整数解为
________;
(2)不等式x≤3的非负整数解为
____________;
(3)不等式x≥-2的负整数解为_______.
x=1,2
x=0,1,2,3
x=-2,-1
1、根据“当x为任何正数时都能使不等到式x+3>2成立”,能不能说不等式的解集为x>0 为什么
例1、解不等式2(5x+3) ≤x-3(1-2x),并将解集在数轴上表示出来。
解:2(5x+3) ≤x-3(1-2x)
10x+6 ≤x-3+6x
10x-x-6x ≤-3-6
3x ≤-9
x ≤-3
在数轴上表示如图所示:
0
1
-1
-2
-3
-4
例2、解不等式
≥
解:
2(x+2) ≥3(3x+4)+30
2x+4 ≥ 9x+12+30
2x -9x≥12+30-4
-7x≥38
x≤
≥
解一元一次不等式的一般步骤
(1)去分母:
各项都乘以分母的最小公倍数;
(2)去括号:注意符号问题、不漏乘;
(3)移 项:
(4)合并同类项:
(5)系数化1:
移动的项要变号;
系数相加减,字母及字母的指数不变;
不等式两边同时除以未知数的系数。
第1步和第5步乘(或除以)同一个负数时要改变不等号方向。
注意:
解下列不等式,并将解集在数轴上表示出来: (1) 2x-1<4x+13
解: 2x-1<4x+13
2x-4x<13+1
-2x<14
x>-7
它在数轴上的表示如图所示
1
2
-2
-1
0
-4
-5
-6
-7
-8
-3
它在数轴上的表示如下:
2
0
3
0
它在数轴上的表示如下:
4解不等式
解:
观察不等式解题过程:
两边同乘以6
两边同乘以-1
正确解法:
不等号方 向改变
解:
例3.当x为何值时,代数式 与 的值的差不大于1?
3(2x+3)-2(x+1)≤6
6x+9-2x-2≤6
6x-2x≤6-9+2
4x≤ -1
x≤
所以,当x取不大于 的任何数时,代数式 与 的值的差不大于1。
解:根据题意,得
已知关于x的方程 3x-m= x- 5
4
3
的解大于0,求m的取值范围.
2.已知方程组的解x、y满足
X+y>-1,求a的取值范围:
◣ ◢
你的思路是什么?
中考展望
X-y=2a
X+3y=1-5a
三个连续正奇数的和小于30,这样
的数有几组?把它们分别写出来.
若不等式x-a≤0只有3个正整数解,求正整数a的取值范围.
若x<a的解集中最大的整数解为3,
则a的取值范围为 .
3<a≤4
若x<a的解集中最大的整数解为3,
则a的取值范围为 .
3<a≤4
若x<a的解集中最大的整数解为3,
则a的取值范围为 .
3<a≤4
若x<a的解集中最大的整数解为3,
则a的取值范围为 .
3<a≤4
根据以下图形,写出不等式的解集:
(1)
( )
(2)
( )
(3)
( )
x≤4
x>2
x≥-2
大于向右,小于向左,有等号为实心,无等号为空心.
(1)x≤-1 (2)x≥-3
(3)x<2 (4)-3≤x<2
在数轴上表示下列不等式的解集:
答:整数解为-1、0、1、2、3,
其中x的最大整数值为3.
⒈你能求出适合不等式-1≤x<4的整数
解吗?其中的x的最大整数值是多少呢?
复习回顾
一.等式的性质
等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.
如果a=b,那么a±c=b±c
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
如果a=b,那么ac=bc或 (c≠0),
不等式是否具有类似的性质呢?
如果 5 > 3
那么 5+2 ____ 3+2 , 5 -2____3-2
>
>
如果-1< 3,
那么-1+2____3+2, -1- 3____3 - 3
<
<
性质1 :如果 a>b, 那么 a+c>b+c 或 a-c>b-c
即:不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变.
6÷5 ____ 2÷ 5 ,
6 ÷ (-5)____2÷ (-5)
不等式两边都乘以(或除以)同一个不为零的数,不等号的方向是否改变?
如果 6 >2
那么 6×5 ____ 2× 5 ,
6 ×(-5)____2×(-5),
>
如果-2< 3,
那么-2×6____3×6,
-2×(- 6)____3×( - 6),
-2÷2____3÷2,
-2÷ (- 4)____3÷ ( - 4)
>
>
<
<
<
<
>
发现:同乘以一个正数,不等号方向不变,同乘以一个 负数不等号方向改变,同乘以0的时候相等.
<
>
>
>
<
<
=
猜想2:不等式两边都乘以(或除以)同一个不为零的数,不等号
的方向是否改变?
正数:7×3 4×3 负数:7×(-1) 4 × (-1)
7×2 4×2 7 ×(-2) 4 × (-2)
7×1 4×1 7 × (-3) 4 × (-3)
零: 7×0 4×0
将不等式 7>4 的两边都乘以同一个数,比较所得结果的大小,
用 >、< 、= 填空
举例分析:
不等式基本性质2:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
不等式基本性质3:不等式的两边都乘以(或除以)同一个____,不等号的方向____。
如果________,那么______________
不变
正数
a>b,c>0
ac>bc (或 )
负数
改变
如果________,那么______________
a>b,c<0
ac
判断下列各题的推导是否正确?为什么(学生口答)
(1)因为7.5>5.7,所以-7.5<-5.7;
(2)因为a+8>4,所以a>-4;
(3)因为4a>4b,所以a>b;
(4)因为-1>-2,所以-a-1>-a-2;
(5)因为3>2,所以3a>2a.
答:
.
(1)正确,根据不等式基本性质3.
(2)正确,根据不等式基本性质1.
(3)正确,根据不等式基本性质2.
(4)正确,根据不等式基本性质1.
(5)不对,应分情况逐一讨论.
当a>0时,3a>2a.(不等式基本性质2)
当 a=0时,3a=2a.
当a<0时,3a<2a.(不等式基本性质3)
我是最棒的
选择适当的不等号填空:
(1)∵0 1,
∴ a a+1(不等式的基本性质1);
(2)∵(a-1)2 0,
∴(a-1)2-2 -2(不等式的基本性质1)
(3)若x+1>0,两边同加上-1,得____________
(依据:_____________________).
(4)若2 x >-6,两边同除以2,得________,依据_______________.
(5)若-0.5 x≤1,两边同乘以-2,得________,依据___________
<
<
≥
≥
x >-1
不等式的基本性质1
x >-3
不等式的基本性质2
X≥-2
不等式的基本性质3
试一试
1.若-m>5,则m -5.
2.如果x/y>0, 那么xy 0.
3.如果a>-1,那么a-b -1-b.
4.-0.9<-0.3,两边都除以(-0.3),得_______.
>
>
<
3 >1
例 已知a<0 ,试比较2a与a的大小。
解法一:∵2>1,a<0,
∴2a<a(不等式的基本性质3)
解法二: 在数轴上分别表示2a和a的点(a<0),如图.2a位于a的左边,所以2a<a
0
a
2a
∣a∣
∣a∣
想一想:还有其他比较2a与a的大小的方法吗?
∵ 2a-a=a, 又∵ a<0,
∴ 2a-a<0,
∴2a
(1)不等式的两边都加上(或减去)同一个数或同一个式子,不等号的方向不变.
(2) 不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
(3) 不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
知 识 回 顾
解:(1) x-2+2<3+2
x<5
(2) 6x-5x<5x-1-5x
x<-1
例1.根据不等式的基本性质,把下列不等式化成
x<a 或x>a的形式:
x-2< 3 (2) 6x< 5x-1
:解不等式:
(1)x-7<8 (2)3x<2x-3
这两小题中不等式的变形与方程的什么变形相类似?
解:
解:
x-7+7 <8+7
3x-2x <2x-3-2x
移
移
x <8+7
x <15
3x-2x <-3
x <-3
这里的变形与方程中的移项相类似:
注意:移项要变号
例题解析
这两小题中不等式的变形与方程的什么变形相类似?有什么不同?
解(1)
(2)
与解方程一样,
解不等式的过程,
就是要将不等式
变形成x>a或x
不等式两边同乘以负数要改变不等号的方向
学习离不开总结!
通过今天的探讨学习,你获得了哪些新知识 大胆说出来,和大家交流一下!
1、解一元一次不等式的依据
如果a>b,那么a+c>b+c,a-c>b-c
如果a>b,并且c>0,那么ac>bc。
如果a>b,并且c<0,那么ac
2、解一元一次不等式的步骤与解一元一次方程的异同点
不等式两边同乘以负数要改变不等号的方向
解一元一次不等式的基本步骤:
(1);移项;
(2)合并同类项;
(3)化系数为1.
解下列不等式,并在数轴上表示出来:
1、X-2>0 2、X+1>0
3、-2x<4 4、3x+3≤0
解:x >2
-3
-2
-1
0
4
2
1
3
5
。
x >-1
-3
-2
-1
0
4
2
1
3
5
x >-2
-3
-2
-1
0
4
2
1
3
5
。
x ≤-1
-3
-2
-1
0
4
2
1
3
5
.
。
试一试,可要仔细呦!
求不等式1-2x < 6的负整数解
发挥集体的智慧,让我们共同努力
思考:要知道x的负整数解,首先应该求出一元一次此不等式x的解集.
要使x的解是负整数,则x还必须小于0
所以不等式的负整数解为 -2 、-1
1-2x < 6
不等式x< 的正整数解为
________;
(2)不等式x≤3的非负整数解为
____________;
(3)不等式x≥-2的负整数解为_______.
x=1,2
x=0,1,2,3
x=-2,-1
1、根据“当x为任何正数时都能使不等到式x+3>2成立”,能不能说不等式的解集为x>0 为什么
例1、解不等式2(5x+3) ≤x-3(1-2x),并将解集在数轴上表示出来。
解:2(5x+3) ≤x-3(1-2x)
10x+6 ≤x-3+6x
10x-x-6x ≤-3-6
3x ≤-9
x ≤-3
在数轴上表示如图所示:
0
1
-1
-2
-3
-4
例2、解不等式
≥
解:
2(x+2) ≥3(3x+4)+30
2x+4 ≥ 9x+12+30
2x -9x≥12+30-4
-7x≥38
x≤
≥
解一元一次不等式的一般步骤
(1)去分母:
各项都乘以分母的最小公倍数;
(2)去括号:注意符号问题、不漏乘;
(3)移 项:
(4)合并同类项:
(5)系数化1:
移动的项要变号;
系数相加减,字母及字母的指数不变;
不等式两边同时除以未知数的系数。
第1步和第5步乘(或除以)同一个负数时要改变不等号方向。
注意:
解下列不等式,并将解集在数轴上表示出来: (1) 2x-1<4x+13
解: 2x-1<4x+13
2x-4x<13+1
-2x<14
x>-7
它在数轴上的表示如图所示
1
2
-2
-1
0
-4
-5
-6
-7
-8
-3
它在数轴上的表示如下:
2
0
3
0
它在数轴上的表示如下:
4解不等式
解:
观察不等式解题过程:
两边同乘以6
两边同乘以-1
正确解法:
不等号方 向改变
解:
例3.当x为何值时,代数式 与 的值的差不大于1?
3(2x+3)-2(x+1)≤6
6x+9-2x-2≤6
6x-2x≤6-9+2
4x≤ -1
x≤
所以,当x取不大于 的任何数时,代数式 与 的值的差不大于1。
解:根据题意,得
已知关于x的方程 3x-m= x- 5
4
3
的解大于0,求m的取值范围.
2.已知方程组的解x、y满足
X+y>-1,求a的取值范围:
◣ ◢
你的思路是什么?
中考展望
X-y=2a
X+3y=1-5a
三个连续正奇数的和小于30,这样
的数有几组?把它们分别写出来.
若不等式x-a≤0只有3个正整数解,求正整数a的取值范围.
若x<a的解集中最大的整数解为3,
则a的取值范围为 .
3<a≤4
若x<a的解集中最大的整数解为3,
则a的取值范围为 .
3<a≤4
若x<a的解集中最大的整数解为3,
则a的取值范围为 .
3<a≤4
若x<a的解集中最大的整数解为3,
则a的取值范围为 .
3<a≤4
