华师版七年级上册数学 5.1.4同位角、内错角、同旁内角【学案】
文档属性
| 名称 | 华师版七年级上册数学 5.1.4同位角、内错角、同旁内角【学案】 |
|
|
| 格式 | doc | ||
| 文件大小 | 124.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 10:32:20 | ||
图片预览

文档简介
同位角、内错角、同旁内角
学习目标:
1.知道同位角、内错角、同旁内角的概念;
2.会识别同位角、内错角、同旁内角.养成善于观察、勤于动脑的好习惯;
重点:识别同位角、内错角、同旁内角.
难点:根据图形特点正确确定位置关系的角.
预习导学——不看不讲
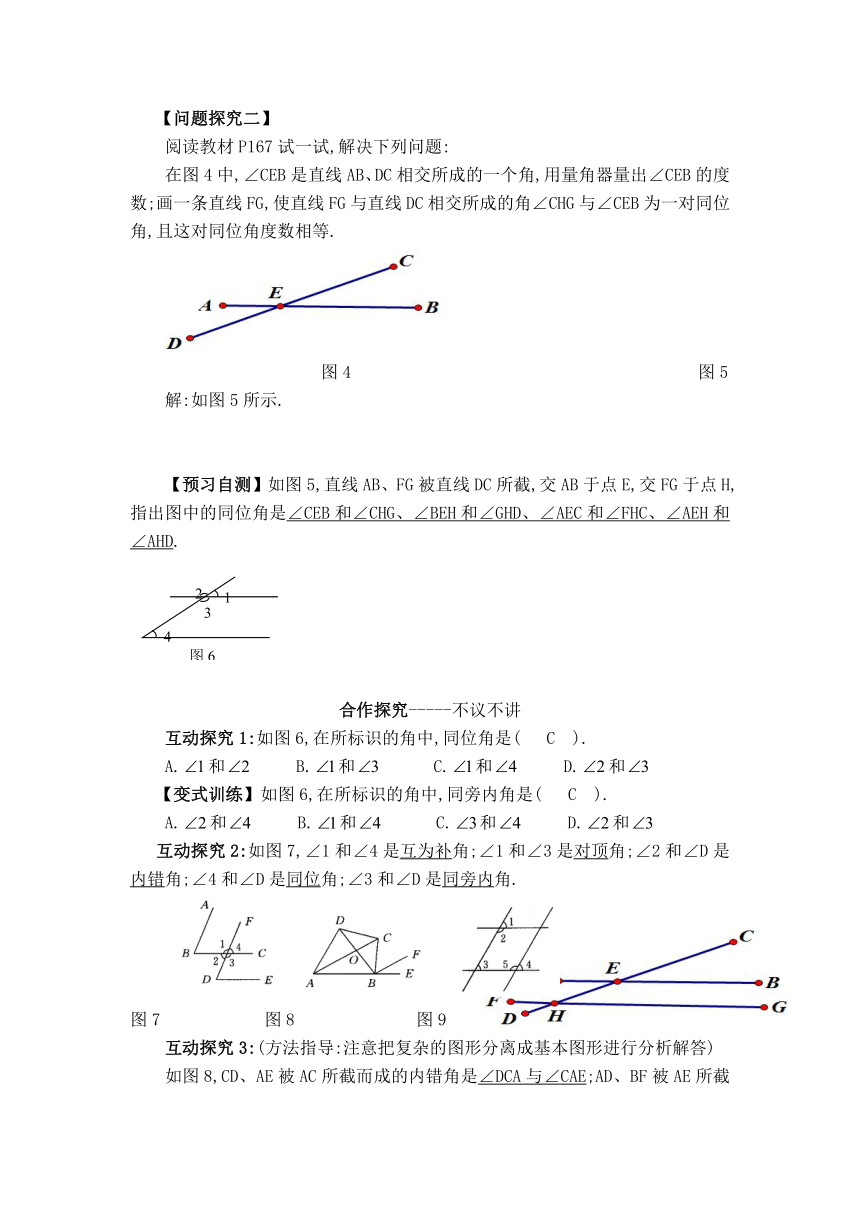
【旧知回顾】如图1,直线AB、CD相交于点O,形成了四个角.
(1)图中有2对对顶角;
(2)图中有4对互为补角.
【问题】
阅读教材P166~P167“试一试”上面的内容,解决下列问题。
直线l截直线a、b,得到八个角.
1.图2中的∠1与∠5的位置有什么关系?从直线l来看,∠1与∠5处于哪个位置?从直线a、b来看,∠1与∠5处于哪个位置?∠1与∠5处于直线l的同一侧,且分别在直线a、b的同一方,这样位置的一对角就是同位角.
2.图2中的∠3与∠5的位置有什么关系?从直线l来看,∠3与∠5处于哪个位置?从直线a、b来看,∠3与∠5处于哪个位置?∠3与∠5处于直线l的两侧,且分别在直线a、b之间,这样位置的一对角就是内错角.
3.图2中的∠4与∠5的位置有什么关系?从直线l来看,∠4与∠5处于哪个位置?从直线a、b来看,∠4与∠5处于哪个位置?∠4与∠5处于直线l的同一侧,且分别在直线a、b之间,这样位置的一对角就是同旁内角.
【归纳总结】处于一条直线的同一侧,且分别在两条直线的同一方的一对角叫做同位角;处于一条直线的两侧,且分别在两条直线之间的一对角叫做内错角;处于一条直线的同一侧,且分别在两条直线之间的一对角叫做同旁内角.
【预习自测】如图3,∠1与∠4是直线b、c被直线a所截的同位角.∠3与∠4是直线b、c被直线a所截的同旁内角.
【问题探究二】
阅读教材P167试一试,解决下列问题:
在图4中,∠CEB是直线AB、DC相交所成的一个角,用量角器量出∠CEB的度数;画一条直线FG,使直线FG与直线DC相交所成的角∠CHG与∠CEB为一对同位角,且这对同位角度数相等.
图4 图5
解:如图5所示.
【预习自测】如图5,直线AB、FG被直线DC所截,交AB于点E,交FG于点H,指出图中的同位角是∠CEB和∠CHG、∠BEH和∠GHD、∠AEC和∠FHC、∠AEH和∠AHD.
合作探究-----不议不讲
互动探究1:如图6,在所标识的角中,同位角是( C ).
A.和 B.和 C.和 D.和
【变式训练】如图6,在所标识的角中,同旁内角是( C ).
A.和 B.和 C.和 D.和
互动探究2:如图7,∠1和∠4是互为补角;∠1和∠3是对顶角;∠2和∠D是内错角;∠4和∠D是同位角;∠3和∠D是同旁内角.
图7 图8 图9
互动探究3:(方法指导:注意把复杂的图形分离成基本图形进行分析解答)
如图8,CD、AE被AC所截而成的内错角是∠DCA与∠CAE;AD、BF被AE所截而成的同位角是∠DAE与∠FBE;BD、AE被AD所截而成的同旁内角是∠ADB与∠DAB.
互动探究4:如图9,已知∠1=60°,∠2+∠3=180°,∠3=∠4,求∠5的度数.
解:因为∠1+∠2=180°,∠1=60°,所以∠2=120°.因为∠2+∠3=180°,所以∠3=60°.
因为∠3=∠4,所以∠4=60°.因为∠4+∠5=180°,所以∠5=120°.
【方法归纳交流】解同位角、内错角、同旁内角的有关问题应先找出哪两条直线被第三条直线所截,再利用同位角、内错角、同旁内角的概念去找.
【达标测评】
基础题―――初显身手
1.在图1所标识的角中,同位角是( ).
A.和 B.和
C.和 D.和
图2
2.在图1所标识的角中,内错角是( ).
A.和 B.和
C.和 D.和
3.如图2,∠1与∠2是内错角,∠1与∠3是________,∠2与∠3是____.
4.如图3,l分别与、相交,若∠1=∠3,试说明∠2=∠4.
图3 图4
能力题―――挑战自我
5.在下列图中,∠1与∠2不是同位角的是( ).
6.在图4中,下列判断正确的是( ).
A.2对同位角、2对内错角、2对同旁内角
B.2对同位角、2对内错角、3对同旁内角
C.4对同位角、2对内错角、4对同旁内角
D.以上判断都不正确
7.在图5中,∠ABC与____是同位角,∠ABC与____是同旁内角,∠ADB与____是内错角.
图5 图6
8.在图6中,直线AB、DC被直线BC所截的同旁内角是________;∠CAB和∠ACD是直线AB、DC被直线AC所截的________.
学习目标:
1.知道同位角、内错角、同旁内角的概念;
2.会识别同位角、内错角、同旁内角.养成善于观察、勤于动脑的好习惯;
重点:识别同位角、内错角、同旁内角.
难点:根据图形特点正确确定位置关系的角.
预习导学——不看不讲
【旧知回顾】如图1,直线AB、CD相交于点O,形成了四个角.
(1)图中有2对对顶角;
(2)图中有4对互为补角.
【问题】
阅读教材P166~P167“试一试”上面的内容,解决下列问题。
直线l截直线a、b,得到八个角.
1.图2中的∠1与∠5的位置有什么关系?从直线l来看,∠1与∠5处于哪个位置?从直线a、b来看,∠1与∠5处于哪个位置?∠1与∠5处于直线l的同一侧,且分别在直线a、b的同一方,这样位置的一对角就是同位角.
2.图2中的∠3与∠5的位置有什么关系?从直线l来看,∠3与∠5处于哪个位置?从直线a、b来看,∠3与∠5处于哪个位置?∠3与∠5处于直线l的两侧,且分别在直线a、b之间,这样位置的一对角就是内错角.
3.图2中的∠4与∠5的位置有什么关系?从直线l来看,∠4与∠5处于哪个位置?从直线a、b来看,∠4与∠5处于哪个位置?∠4与∠5处于直线l的同一侧,且分别在直线a、b之间,这样位置的一对角就是同旁内角.
【归纳总结】处于一条直线的同一侧,且分别在两条直线的同一方的一对角叫做同位角;处于一条直线的两侧,且分别在两条直线之间的一对角叫做内错角;处于一条直线的同一侧,且分别在两条直线之间的一对角叫做同旁内角.
【预习自测】如图3,∠1与∠4是直线b、c被直线a所截的同位角.∠3与∠4是直线b、c被直线a所截的同旁内角.
【问题探究二】
阅读教材P167试一试,解决下列问题:
在图4中,∠CEB是直线AB、DC相交所成的一个角,用量角器量出∠CEB的度数;画一条直线FG,使直线FG与直线DC相交所成的角∠CHG与∠CEB为一对同位角,且这对同位角度数相等.
图4 图5
解:如图5所示.
【预习自测】如图5,直线AB、FG被直线DC所截,交AB于点E,交FG于点H,指出图中的同位角是∠CEB和∠CHG、∠BEH和∠GHD、∠AEC和∠FHC、∠AEH和∠AHD.
合作探究-----不议不讲
互动探究1:如图6,在所标识的角中,同位角是( C ).
A.和 B.和 C.和 D.和
【变式训练】如图6,在所标识的角中,同旁内角是( C ).
A.和 B.和 C.和 D.和
互动探究2:如图7,∠1和∠4是互为补角;∠1和∠3是对顶角;∠2和∠D是内错角;∠4和∠D是同位角;∠3和∠D是同旁内角.
图7 图8 图9
互动探究3:(方法指导:注意把复杂的图形分离成基本图形进行分析解答)
如图8,CD、AE被AC所截而成的内错角是∠DCA与∠CAE;AD、BF被AE所截而成的同位角是∠DAE与∠FBE;BD、AE被AD所截而成的同旁内角是∠ADB与∠DAB.
互动探究4:如图9,已知∠1=60°,∠2+∠3=180°,∠3=∠4,求∠5的度数.
解:因为∠1+∠2=180°,∠1=60°,所以∠2=120°.因为∠2+∠3=180°,所以∠3=60°.
因为∠3=∠4,所以∠4=60°.因为∠4+∠5=180°,所以∠5=120°.
【方法归纳交流】解同位角、内错角、同旁内角的有关问题应先找出哪两条直线被第三条直线所截,再利用同位角、内错角、同旁内角的概念去找.
【达标测评】
基础题―――初显身手
1.在图1所标识的角中,同位角是( ).
A.和 B.和
C.和 D.和
图2
2.在图1所标识的角中,内错角是( ).
A.和 B.和
C.和 D.和
3.如图2,∠1与∠2是内错角,∠1与∠3是________,∠2与∠3是____.
4.如图3,l分别与、相交,若∠1=∠3,试说明∠2=∠4.
图3 图4
能力题―――挑战自我
5.在下列图中,∠1与∠2不是同位角的是( ).
6.在图4中,下列判断正确的是( ).
A.2对同位角、2对内错角、2对同旁内角
B.2对同位角、2对内错角、3对同旁内角
C.4对同位角、2对内错角、4对同旁内角
D.以上判断都不正确
7.在图5中,∠ABC与____是同位角,∠ABC与____是同旁内角,∠ADB与____是内错角.
图5 图6
8.在图6中,直线AB、DC被直线BC所截的同旁内角是________;∠CAB和∠ACD是直线AB、DC被直线AC所截的________.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
