华师版七年级上册数学 5.2.3平行线的性质【学案】
文档属性
| 名称 | 华师版七年级上册数学 5.2.3平行线的性质【学案】 |

|
|
| 格式 | doc | ||
| 文件大小 | 148.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-13 00:00:00 | ||
图片预览

文档简介
平行线的性质
学习目标:
1、探索平行线的性质,并掌握它们的文字语言、符号语言和图形语言。
2、会用平行线的性质进行简单的计算和推理,结合平行线对图形进行简单的平移。
重点:掌握平行线的性质。
难点:平行线的性质与判定的区别。
【一】复习引入
回顾“三线八角”
指出下列各图中所有的同位角、内错角、同旁内角
2、下列各图中 与哪些是同位角?哪些不是?
3、如图,
(1)和 是直线_____与直线____被直线______所截形成的__________。
(2)和 是直线_____与直线____被直线______所截形成的_________。
A 3 D
4
1
B 2 C
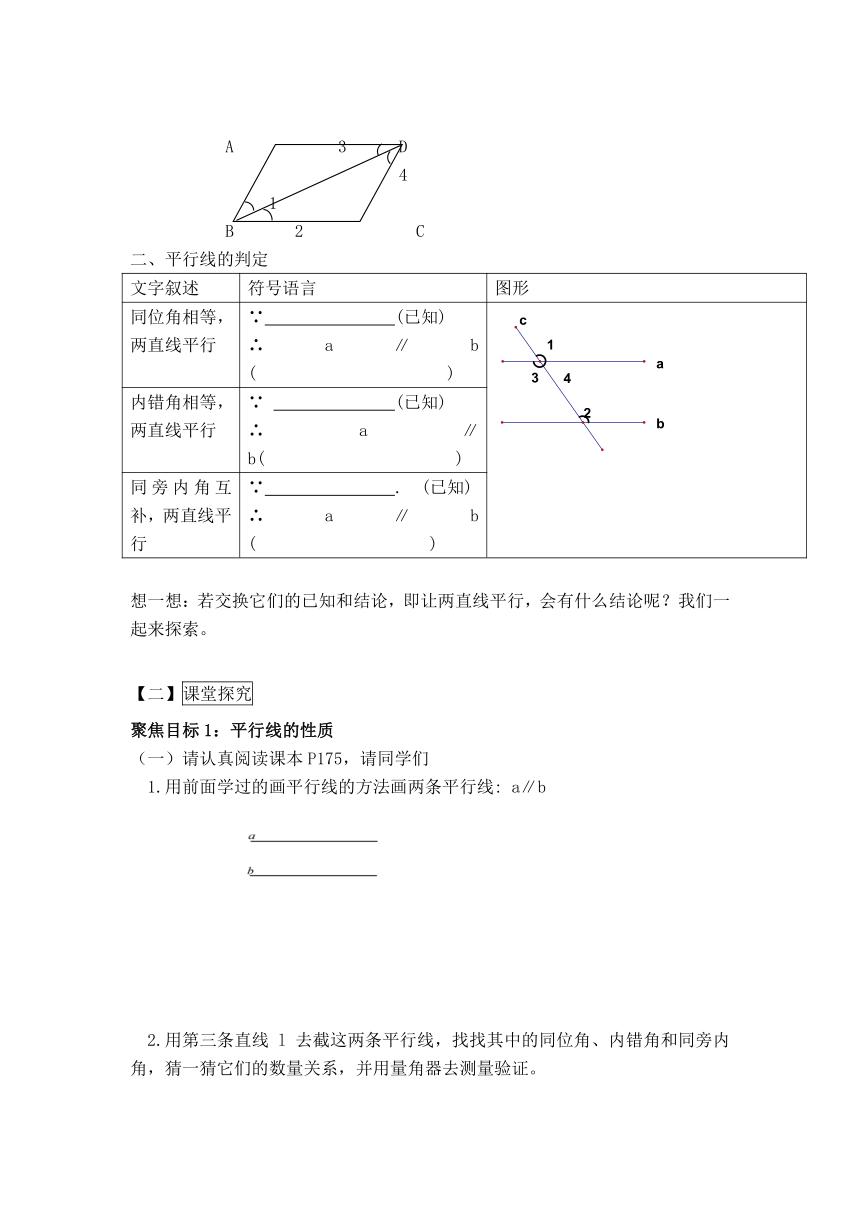
平行线的判定
文字叙述 符号语言 图形
同位角相等,两直线平行 ∵ (已知)
∴a∥b ( )
内错角相等,两直线平行 ∵ (已知)
∴a∥b( )
同旁内角互补,两直线平行 ∵ . (已知)
∴a∥b ( )
想一想:若交换它们的已知和结论,即让两直线平行,会有什么结论呢?我们一起来探索。
【二】课堂探究
聚焦目标1:平行线的性质
(一)请认真阅读课本P175,请同学们
1.用前面学过的画平行线的方法画两条平行线: a∥b
2.用第三条直线 l 去截这两条平行线,找找其中的同位角、内错角和同旁内角,猜一猜它们的数量关系,并用量角器去测量验证。
3.归纳你得到的结论:填写如下表格。
文字叙述 符号语言 图形
两直线平行,同位角相等 ∵a∥b (已知)
∴______________( )
两直线平行,内错角相等 ∵a∥b(已知)
∴______________( )
两直线平行,同旁内角互补 ∵a∥b (已知)
∴______________( )
【三】合作练习
师生互动共同完成下面的例题。
例2 如图,在四边形ABCD中,已知AB∥CD,∠B=60°,求
∠C的度数。能否求得∠A的度数 ?
分析:由于AB∥CD ,
根据两直线平行,同旁内角互补 ,
可得____________________。
又∠B=60° ,因此∠C=___________ 。
根据题目的已知条件,无法求出 ∠A的度数。
解:
四】小结(教师提问)
(1)平行线的判定
(2)平行线的性质
(3)理解平行线的判定与性质的区别。
【五】课后检测。
1.如图1,已知∠1 = 100°,AB∥CD,则∠2 = ,∠3 = ,∠4 = .
2.如图2,直线AB、CD被EF所截,若∠1 =∠2,则∠AEF +∠CFE = .
3.如图3所示
(1)若EF∥AC,则∠A +∠ = 180°,∠F + ∠ = 180°( ).
(2)若∠2 =∠ ,则AE∥BF.
(3)若∠A +∠ = 180°,则AE∥BF.
4.如图4,AB∥CD,∠2 = 2∠1,则∠2 = .
5.如右图,a∥b,a、b被c所截,得到∠1=∠2的依据是( )
A.两直线平行,同位角相等 B.两直线平行,内错角相等
C.同位角相等,两直线平行 D.内错角相等,两直线平行
6.如图6,推理填空:
(1)∵∠A =∠ (已知),
∴AC∥ED( );
(2)∵∠2 =∠ (已知),
∴AC∥ED( );
(3)∵∠A +∠ = 180°(已知),
∴AB∥FD( );
(4)∵∠2 +∠ = 180°(已知),
∴AC∥ED( );
学习目标:
1、探索平行线的性质,并掌握它们的文字语言、符号语言和图形语言。
2、会用平行线的性质进行简单的计算和推理,结合平行线对图形进行简单的平移。
重点:掌握平行线的性质。
难点:平行线的性质与判定的区别。
【一】复习引入
回顾“三线八角”
指出下列各图中所有的同位角、内错角、同旁内角
2、下列各图中 与哪些是同位角?哪些不是?
3、如图,
(1)和 是直线_____与直线____被直线______所截形成的__________。
(2)和 是直线_____与直线____被直线______所截形成的_________。
A 3 D
4
1
B 2 C
平行线的判定
文字叙述 符号语言 图形
同位角相等,两直线平行 ∵ (已知)
∴a∥b ( )
内错角相等,两直线平行 ∵ (已知)
∴a∥b( )
同旁内角互补,两直线平行 ∵ . (已知)
∴a∥b ( )
想一想:若交换它们的已知和结论,即让两直线平行,会有什么结论呢?我们一起来探索。
【二】课堂探究
聚焦目标1:平行线的性质
(一)请认真阅读课本P175,请同学们
1.用前面学过的画平行线的方法画两条平行线: a∥b
2.用第三条直线 l 去截这两条平行线,找找其中的同位角、内错角和同旁内角,猜一猜它们的数量关系,并用量角器去测量验证。
3.归纳你得到的结论:填写如下表格。
文字叙述 符号语言 图形
两直线平行,同位角相等 ∵a∥b (已知)
∴______________( )
两直线平行,内错角相等 ∵a∥b(已知)
∴______________( )
两直线平行,同旁内角互补 ∵a∥b (已知)
∴______________( )
【三】合作练习
师生互动共同完成下面的例题。
例2 如图,在四边形ABCD中,已知AB∥CD,∠B=60°,求
∠C的度数。能否求得∠A的度数 ?
分析:由于AB∥CD ,
根据两直线平行,同旁内角互补 ,
可得____________________。
又∠B=60° ,因此∠C=___________ 。
根据题目的已知条件,无法求出 ∠A的度数。
解:
四】小结(教师提问)
(1)平行线的判定
(2)平行线的性质
(3)理解平行线的判定与性质的区别。
【五】课后检测。
1.如图1,已知∠1 = 100°,AB∥CD,则∠2 = ,∠3 = ,∠4 = .
2.如图2,直线AB、CD被EF所截,若∠1 =∠2,则∠AEF +∠CFE = .
3.如图3所示
(1)若EF∥AC,则∠A +∠ = 180°,∠F + ∠ = 180°( ).
(2)若∠2 =∠ ,则AE∥BF.
(3)若∠A +∠ = 180°,则AE∥BF.
4.如图4,AB∥CD,∠2 = 2∠1,则∠2 = .
5.如右图,a∥b,a、b被c所截,得到∠1=∠2的依据是( )
A.两直线平行,同位角相等 B.两直线平行,内错角相等
C.同位角相等,两直线平行 D.内错角相等,两直线平行
6.如图6,推理填空:
(1)∵∠A =∠ (已知),
∴AC∥ED( );
(2)∵∠2 =∠ (已知),
∴AC∥ED( );
(3)∵∠A +∠ = 180°(已知),
∴AB∥FD( );
(4)∵∠2 +∠ = 180°(已知),
∴AC∥ED( );
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
