7.2.4诱导公式 课件(共31张PPT)-2020-2021学年高一下学期数学人教B版(2019)必修第三册
文档属性
| 名称 | 7.2.4诱导公式 课件(共31张PPT)-2020-2021学年高一下学期数学人教B版(2019)必修第三册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览








文档简介
(共31张PPT)
课程名称:7.2.4诱导公式
学
科:数学
年
级:高一
教材版本:人教B版2019
问题情境
如果已知sin26°=m,你能用m表示出sin386°,sin(-26°),sin154°,sin206°吗?你还能用m表示出更多角的三角函数值吗?
学习目标:
1.借助单位圆的对称性,利用三角函数定义推导诱导公式(1)--(4),从数和形形两方面去理解记忆公式;
2.能运用诱导公式解决简单的三角求值、化简问题;
3.通过推导诱导公式,体会由特殊到一般、转化与化归的数学思想,在应用中提升数学运算和逻辑推理的核心素养。
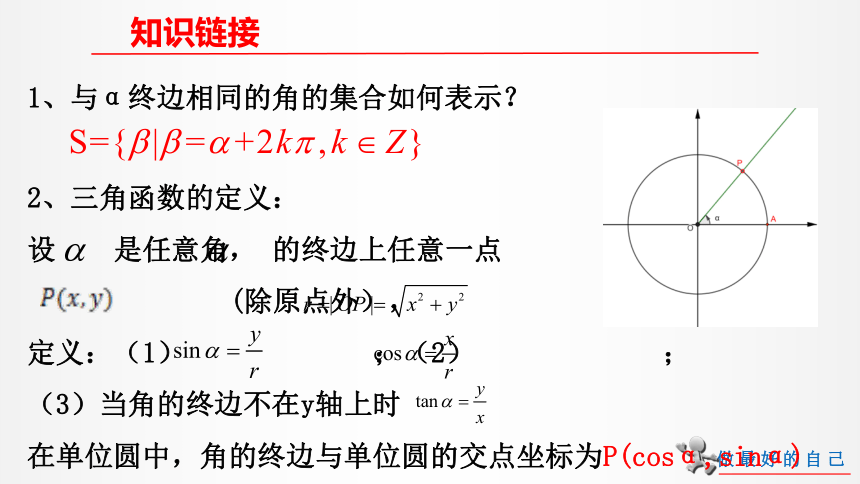
知识链接
1、与α终边相同的角的集合如何表示?
2、三角函数的定义:
设
是任意角,
的终边上任意一点
(除原点外),
定义:(1)
;(2)
;
(3)当角的终边不在y轴上时
在单位圆中,角的终边与单位圆的交点坐标为P(cosα,sinα)
y
x
o
(
)
(
)
(
)
(
)
y
x
o
(
)
(
)
(
)
(
)
y
x
o
(
)
(
)
(
)
(
)
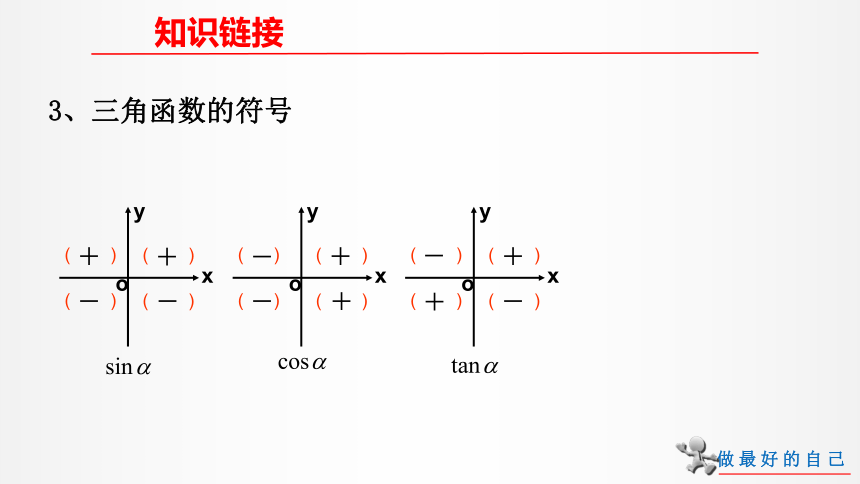
3、三角函数的符号
知识链接
情境探究一
探究一:sin26°=m,sin386°=?
探究提示:寻找26°与386°的终边的关系
情境释疑
探究结果:386°=360°+26°
26°与386°的终边相同
与单位圆交点坐标分别为P(cos26°,sin26°)和
Q(cos386°,sin386°)
你能得到什么一般性的结论呢?
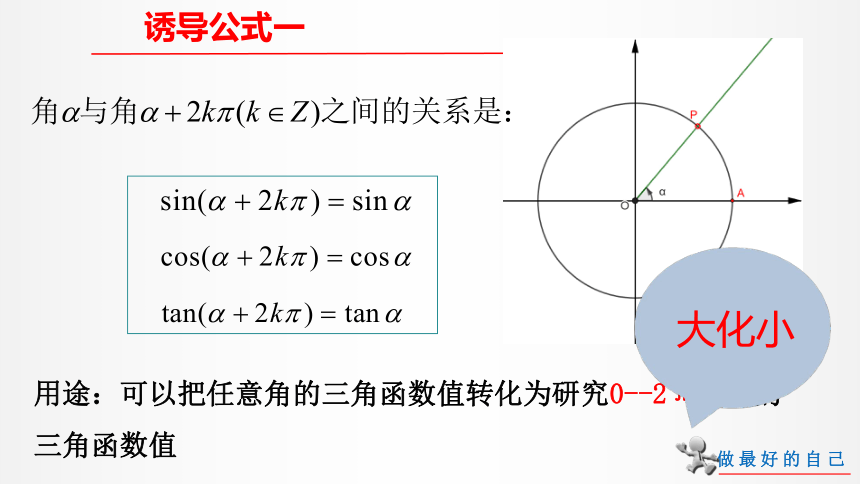
用途:可以把任意角的三角函数值转化为研究0--2π的角的三角函数值
诱导公式一
大化小
例1.求下列各值
例题精讲
解:
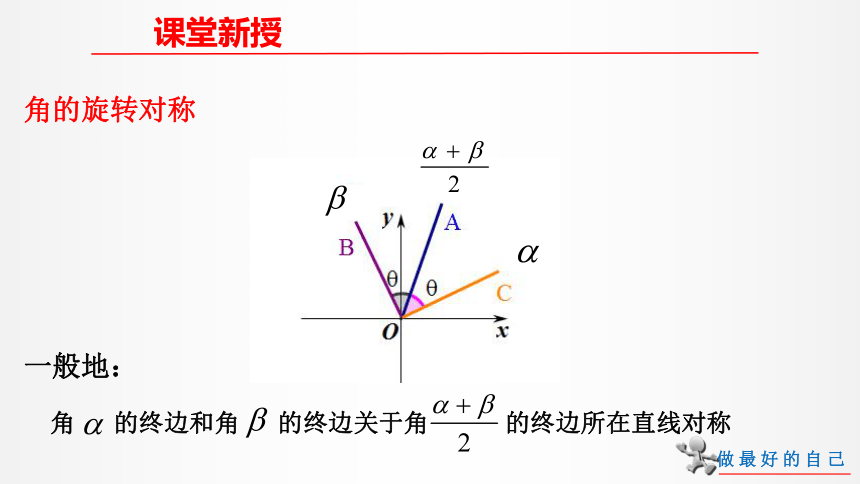
课堂新授
角的旋转对称
角
的终边和角
的终边关于角
的终边所在直线对称
一般地:
①
和
终边关于角
的终边所在直线对称
②
和
终边关于角
的终边所在直线对称
③
和
终边关于角
的终边所在直线对称
举例说明
情境探究二
探究二:sin26°=m,sin(-26°)=?
探究提示:寻找26°与(-26°)的终边的关系,
利用诱导公式一的探究方法
y
x
o
P(cos26°,sin26°)
(1,0)
.
.
.
P’(cos(-26°),sin(-26°))
26°
-26°
sin26°=
-sin(-26°)
cos26°=
cos(-26°)
tan26°=
-tan(-26°)
P
P/
情境释疑
y
x
o
P
(x,y)
(1,0)
.
.
.
P’
α
-α
(x,-y)
诱导公式二
用途:可以把负角的三角函数值转化为正角的三角函数值
负化正
例2.求下列各值
解:
例题精讲
情境探究三
探究三:sin26°=m,
sin154°=?
探究提示:寻找26°与154°的终边的关系
探究结果:26°与154°的终边关于y轴对称
y
x
o
P
(1,0)
.
.
.
26°
154°
P/
P(cos26°,sin26°)
P/(cos154°,sin154°)
sin26°=sin154°
cos26°=-cos154°
tan26°=-tan154°
情境释疑
用途:将
内角的三角函数值
转化为
内的角的三角函数值
诱导公式三
例3.求下列各值
例题精讲
解:
角α的终边与单位圆的交点P(x,y)
y
x
=tanα
y=sinα
x=cosα
角π+α的终边与单位圆的交点
P2(-x,-y)
sin(π+α)=-y=-sinα
tan(π+α)=
y
x
=tanα
cos(π+α)=-x=-cosα
作用:将π~2π的角的三角函数转化为0~π的角的三角函数.
(x,y)
(-x,-y)
诱导公式四
用途:将
内的角的三角函数值转化为
内的角的三角函数值
情境探究
以
代
例4.求下列各值
例题精讲
解:
大角变小角,负角变正角,划到锐角为终了
公式用途
诱导公式①
诱导公式②
诱导公式③
诱导公式④
利用公式①~④把任意角的三角函数转化为锐角函数,一般可按下面步骤进行:
任意角的
三角函数
任意正角的
三角函数
用公式
②或①
锐角三
角函数
用公式
③或④
0~2π的角的三角函数
用公式①
规律探究
公式记忆
诱导公式一
诱导公式二
诱导公式三
诱导公式四
锐角看
函数名不变,符号看象限
问题1:每个公式两边函数名称有什么关系?
问题2:如何确定右侧的符号?
原式
综合应用
例5.化简
课堂小结
1、四组诱导公式,
口诀“函数名不变,符号看象限”
2、通过推导诱导公式,体验化归思想
3、能合理选择公式,能正确运用公式进行化简、求值。
达标检测
1、以下四种化简过程,其中正确的个数是
①
sin(360o+220o)=sin220o
②
sin(180o-220o)=-sin220o
③
sin(180o+220o)=sin220o
④
sin(-220o)=sin220o
A、1
B、2
C、3
D、4
A
2、如果α,β满足α+β=π,那么下列式子中正确的个数是
①sinα=sinβ;②sinα=-sinβ;③cosα=cosβ;④cosα=-cosβ
A、1
B、2
C、3
D、4
B
3、若A,B,C为ΔABC的三内角,则下列等式成立的是
A)
sin(B+C)=sinA
B)
cos(B+C)=cosA
C)
tan(B+C)=tanA
D)
cot(B+C)=cotA
A
1
达标检测
谢谢~
白发无凭吾老矣!青春不再汝知乎?
年将弱冠非童子,学不成名岂丈夫?
——俞良弼
课程名称:7.2.4诱导公式
学
科:数学
年
级:高一
教材版本:人教B版2019
问题情境
如果已知sin26°=m,你能用m表示出sin386°,sin(-26°),sin154°,sin206°吗?你还能用m表示出更多角的三角函数值吗?
学习目标:
1.借助单位圆的对称性,利用三角函数定义推导诱导公式(1)--(4),从数和形形两方面去理解记忆公式;
2.能运用诱导公式解决简单的三角求值、化简问题;
3.通过推导诱导公式,体会由特殊到一般、转化与化归的数学思想,在应用中提升数学运算和逻辑推理的核心素养。
知识链接
1、与α终边相同的角的集合如何表示?
2、三角函数的定义:
设
是任意角,
的终边上任意一点
(除原点外),
定义:(1)
;(2)
;
(3)当角的终边不在y轴上时
在单位圆中,角的终边与单位圆的交点坐标为P(cosα,sinα)
y
x
o
(
)
(
)
(
)
(
)
y
x
o
(
)
(
)
(
)
(
)
y
x
o
(
)
(
)
(
)
(
)
3、三角函数的符号
知识链接
情境探究一
探究一:sin26°=m,sin386°=?
探究提示:寻找26°与386°的终边的关系
情境释疑
探究结果:386°=360°+26°
26°与386°的终边相同
与单位圆交点坐标分别为P(cos26°,sin26°)和
Q(cos386°,sin386°)
你能得到什么一般性的结论呢?
用途:可以把任意角的三角函数值转化为研究0--2π的角的三角函数值
诱导公式一
大化小
例1.求下列各值
例题精讲
解:
课堂新授
角的旋转对称
角
的终边和角
的终边关于角
的终边所在直线对称
一般地:
①
和
终边关于角
的终边所在直线对称
②
和
终边关于角
的终边所在直线对称
③
和
终边关于角
的终边所在直线对称
举例说明
情境探究二
探究二:sin26°=m,sin(-26°)=?
探究提示:寻找26°与(-26°)的终边的关系,
利用诱导公式一的探究方法
y
x
o
P(cos26°,sin26°)
(1,0)
.
.
.
P’(cos(-26°),sin(-26°))
26°
-26°
sin26°=
-sin(-26°)
cos26°=
cos(-26°)
tan26°=
-tan(-26°)
P
P/
情境释疑
y
x
o
P
(x,y)
(1,0)
.
.
.
P’
α
-α
(x,-y)
诱导公式二
用途:可以把负角的三角函数值转化为正角的三角函数值
负化正
例2.求下列各值
解:
例题精讲
情境探究三
探究三:sin26°=m,
sin154°=?
探究提示:寻找26°与154°的终边的关系
探究结果:26°与154°的终边关于y轴对称
y
x
o
P
(1,0)
.
.
.
26°
154°
P/
P(cos26°,sin26°)
P/(cos154°,sin154°)
sin26°=sin154°
cos26°=-cos154°
tan26°=-tan154°
情境释疑
用途:将
内角的三角函数值
转化为
内的角的三角函数值
诱导公式三
例3.求下列各值
例题精讲
解:
角α的终边与单位圆的交点P(x,y)
y
x
=tanα
y=sinα
x=cosα
角π+α的终边与单位圆的交点
P2(-x,-y)
sin(π+α)=-y=-sinα
tan(π+α)=
y
x
=tanα
cos(π+α)=-x=-cosα
作用:将π~2π的角的三角函数转化为0~π的角的三角函数.
(x,y)
(-x,-y)
诱导公式四
用途:将
内的角的三角函数值转化为
内的角的三角函数值
情境探究
以
代
例4.求下列各值
例题精讲
解:
大角变小角,负角变正角,划到锐角为终了
公式用途
诱导公式①
诱导公式②
诱导公式③
诱导公式④
利用公式①~④把任意角的三角函数转化为锐角函数,一般可按下面步骤进行:
任意角的
三角函数
任意正角的
三角函数
用公式
②或①
锐角三
角函数
用公式
③或④
0~2π的角的三角函数
用公式①
规律探究
公式记忆
诱导公式一
诱导公式二
诱导公式三
诱导公式四
锐角看
函数名不变,符号看象限
问题1:每个公式两边函数名称有什么关系?
问题2:如何确定右侧的符号?
原式
综合应用
例5.化简
课堂小结
1、四组诱导公式,
口诀“函数名不变,符号看象限”
2、通过推导诱导公式,体验化归思想
3、能合理选择公式,能正确运用公式进行化简、求值。
达标检测
1、以下四种化简过程,其中正确的个数是
①
sin(360o+220o)=sin220o
②
sin(180o-220o)=-sin220o
③
sin(180o+220o)=sin220o
④
sin(-220o)=sin220o
A、1
B、2
C、3
D、4
A
2、如果α,β满足α+β=π,那么下列式子中正确的个数是
①sinα=sinβ;②sinα=-sinβ;③cosα=cosβ;④cosα=-cosβ
A、1
B、2
C、3
D、4
B
3、若A,B,C为ΔABC的三内角,则下列等式成立的是
A)
sin(B+C)=sinA
B)
cos(B+C)=cosA
C)
tan(B+C)=tanA
D)
cot(B+C)=cotA
A
1
达标检测
谢谢~
白发无凭吾老矣!青春不再汝知乎?
年将弱冠非童子,学不成名岂丈夫?
——俞良弼
