第4章 图形的认识 自我综合评价---同步课时作业 2021-2022学年七年级数学湘教版上册(Word版含答案)
文档属性
| 名称 | 第4章 图形的认识 自我综合评价---同步课时作业 2021-2022学年七年级数学湘教版上册(Word版含答案) | 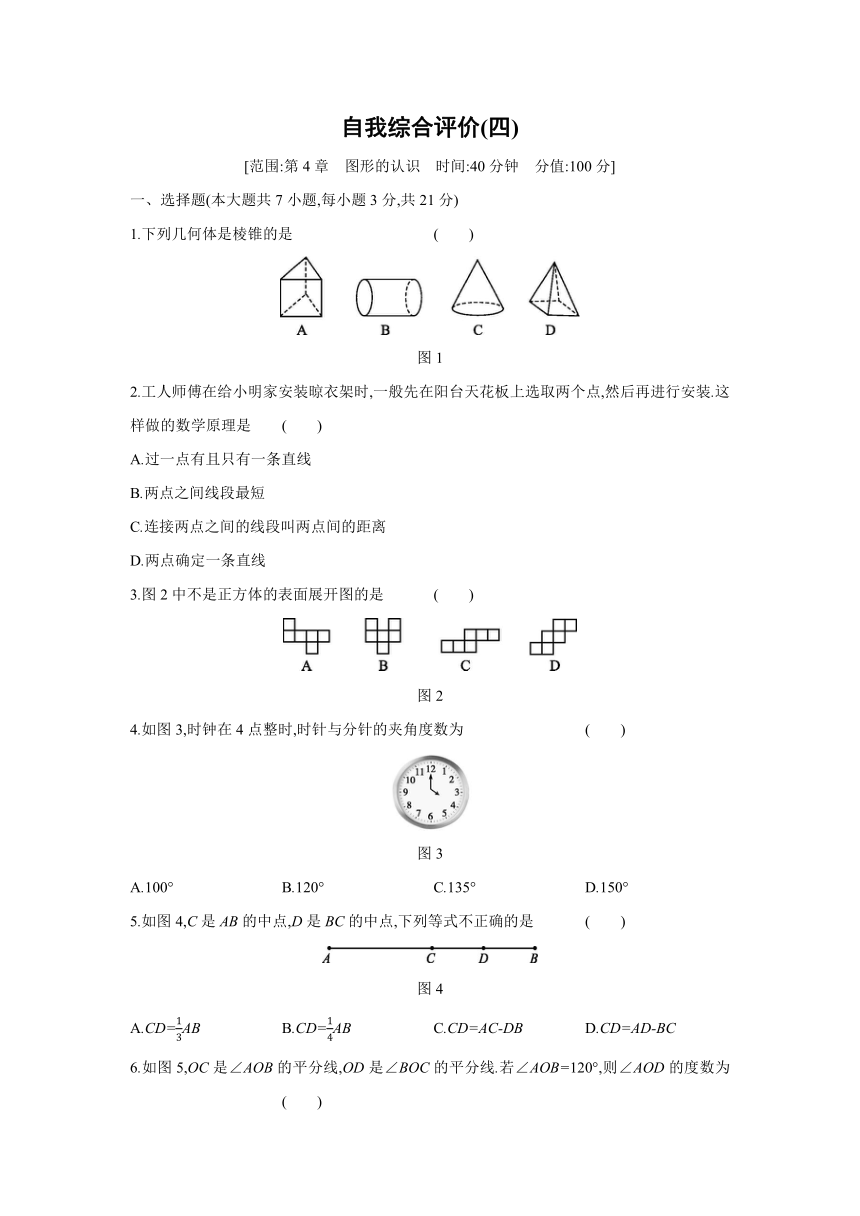 | |
| 格式 | docx | ||
| 文件大小 | 148.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 09:27:06 | ||
图片预览




文档简介
自我综合评价(四)
[范围:第4章 图形的认识 时间:40分钟 分值:100分]
一、选择题(本大题共7小题,每小题3分,共21分)
1.下列几何体是棱锥的是
( )
图1
2.工人师傅在给小明家安装晾衣架时,一般先在阳台天花板上选取两个点,然后再进行安装.这样做的数学原理是
( )
A.过一点有且只有一条直线
B.两点之间线段最短
C.连接两点之间的线段叫两点间的距离
D.两点确定一条直线
3.图2中不是正方体的表面展开图的是
( )
图2
4.如图3,时钟在4点整时,时针与分针的夹角度数为
( )
图3
A.100°
B.120°
C.135°
D.150°
5.如图4,C是AB的中点,D是BC的中点,下列等式不正确的是
( )
图4
A.CD=AB
B.CD=AB
C.CD=AC-DB
D.CD=AD-BC
6.如图5,OC是∠AOB的平分线,OD是∠BOC的平分线.若∠AOB=120°,则∠AOD的度数为
( )
图5
A.30°
B.60°
C.50°
D.90°
7.七年级(4)班杨杰同学在用一副三角尺画角时(即内角分别为30°,60°,90°的一个三角尺,内角分别为45°,45°,90°的一个三角尺),画出了许多不同度数的角,但下列哪个度数的角他画不出来
( )
A.135°
B.75°
C.120°
D.25°
二、填空题(本大题共7小题,每小题3分,共21分)
8.如图6,请从图中抽象出一个图形: .(填一个平面图形或一个立体图形即可)?
图6
9.如图7,图中共有 条线段.?
图7
10.如图8,OB平分∠AOC,∠AOD=78°,∠BOC=20°,则∠COD的度数为 .?
图8
11.已知线段AB,C是AB的中点,E是AC的中点,如果AE=2
cm,那么AB= cm.?
12.若∠α的余角与∠α的补角的和是平角,则∠α的度数为 .?
13.(1)8.31°= ° ' ″;?
(2)78°30'36″= °.?
14.如图9,CE平分∠ACD,∠OCE=105°,则∠OCD= °.?
图9
三、解答题(本大题共6小题,共58分)
15.(8分)如图10,写出下列几何体的名称.
图10
16.(8分)计算:
(1)17°15'23″+25°56'18″;
(2)180°-67°28'43″+21°47'13″.
17.(9分)填空,完成下列说理过程:
如图11,∠AOB=90°,∠COD=90°,OA平分∠DOE,若∠BOC=20°,求∠COE的度数.
解:因为∠AOB=90°,
图11
所以∠BOC+ =90°.?
因为∠COD=90°,
所以∠AOD+ =90°.?
所以∠BOC=∠AOD.( )
因为∠BOC=20°,
所以∠AOD=20°.
因为OA平分∠DOE,
所以∠ =2∠AOD= °.( )?
所以∠COE=∠COD-∠DOE= °.?
18.(9分)如图12,D是AB的中点,E是BC的中点,BE=AC=2
cm,求线段DE的长.
图12
19.(12分)如图13,直线AB,CD,EF相交于点O,∠COB=90°,∠AOE∶∠AOC=2∶5,求∠EOC的度数.
图13
20.(12分)如图14,B是线段AD上一动点,沿A→D以2
cm/s的速度运动,C是线段BD的中点,AD=10
cm,设点B运动的时间为t秒.
(1)当t=2时,
①AB= cm;?
②求线段CD的长度.
(2)在运动过程中,若E是AB的中点,则EC的长是否发生变化?若不变,求出EC的长;若发生变化,请说明理由.
图14
教师详解详析
1.D [解析]
选项A中的图形是三棱柱,不符合题意;
选项B中的图形是圆柱,不符合题意;
选项C中的图形是圆锥,不符合题意;
选项D中的图形是四棱锥,符合题意.
故选D.
2.D [解析]
由两个确定的点定线,其数学原理是“两点确定一条直线”.故选D.
3.B [解析]
由正方体四个侧面和上下两个底面的特征可知,A,C,D选项可以拼成一个正方体,而B选项中出现了“凹”字格,不能拼成正方体.
故选B.
4.B
5.A [解析]
因为C是AB的中点,
所以AC=BC.
因为D是BC的中点,所以CD=DB,
所以CD=DB=AB.
故选项A错误.
6.D [解析]
因为OC是∠AOB的平分线,∠AOB=120°,
所以∠COB=∠AOC=∠AOB=60°.
因为OD是∠BOC的平分线,
所以∠COD=∠BOC=30°.
所以∠AOD=∠COD+∠AOC=90°.故选D.
7.D [解析]
135°,75°,120°的角都是15°角的整倍数,可以画出来.25°角不是15°角的整倍数,不能画出来.故选D.
8.答案不唯一,如圆,圆柱,六棱柱等
9.6 [解析]
图中有线段AB,AC,AD,BC,BD,CD,共6条.
10.38° [解析]
因为OB平分∠AOC,∠BOC=20°,
所以∠AOC=40°.
因为∠AOD=78°,所以∠COD=38°.
11.8 [解析]
因为AE=2
cm,E是AC的中点,
所以AC=2AE=2×2=4(cm).
又因为C是AB的中点,
所以AB=2AC=2×4=8(cm).
故答案为8.
12.45°
13.(1)8 18 36 [解析]
因为0.31°=0.31×60'=18.6',0.6×60″=36″,
所以8.31°=8°18'36″.
(2)78.51 [解析]
因为36×'=0.6',
30.6×°=0.51°,
所以78°30'36″=78.51°.
14.30 [解析]
因为∠OCE=105°,
所以∠ACE=180°-105°=75°.
又因为CE平分∠ACD,
所以∠ACD=2∠ACE=150°.
所以∠OCD=30°.
故答案为30.
15.解:从左往右依次为:长方体、球、圆柱、圆锥、六棱柱、四棱锥.
16.解:(1)原式=42°71'41″=43°11'41″.
(2)原式=112°31'17″+21°47'13″=133°78'30″=134°18'30″.
17.∠AOC ∠AOC 同角的余角相等 DOE 40 角平分线的定义 50
18.解:根据题意,得AC=5BE=10
cm.
因为D是AB的中点,E是BC的中点,
所以DE=DB+BE=AB+BC=AC=5
cm.
19.解:因为∠COB=90°,
所以∠AOC=180°-∠COB=90°.
因为∠AOE∶∠AOC=2∶5,
所以∠AOE==36°.
所以∠EOC=90°-36°=54°.
20.解:(1)①4
②因为AD=10
cm,AB=4
cm,
所以BD=10-4=6(cm).
因为C是线段BD的中点,
所以CD=BD=×6=3(cm).
(2)EC的长不变.
因为E是AB的中点,C是BD的中点,
所以EB=AB,BC=BD.
所以EC=EB+BC=(AB+BD)=AD=×10=5(cm).
[范围:第4章 图形的认识 时间:40分钟 分值:100分]
一、选择题(本大题共7小题,每小题3分,共21分)
1.下列几何体是棱锥的是
( )
图1
2.工人师傅在给小明家安装晾衣架时,一般先在阳台天花板上选取两个点,然后再进行安装.这样做的数学原理是
( )
A.过一点有且只有一条直线
B.两点之间线段最短
C.连接两点之间的线段叫两点间的距离
D.两点确定一条直线
3.图2中不是正方体的表面展开图的是
( )
图2
4.如图3,时钟在4点整时,时针与分针的夹角度数为
( )
图3
A.100°
B.120°
C.135°
D.150°
5.如图4,C是AB的中点,D是BC的中点,下列等式不正确的是
( )
图4
A.CD=AB
B.CD=AB
C.CD=AC-DB
D.CD=AD-BC
6.如图5,OC是∠AOB的平分线,OD是∠BOC的平分线.若∠AOB=120°,则∠AOD的度数为
( )
图5
A.30°
B.60°
C.50°
D.90°
7.七年级(4)班杨杰同学在用一副三角尺画角时(即内角分别为30°,60°,90°的一个三角尺,内角分别为45°,45°,90°的一个三角尺),画出了许多不同度数的角,但下列哪个度数的角他画不出来
( )
A.135°
B.75°
C.120°
D.25°
二、填空题(本大题共7小题,每小题3分,共21分)
8.如图6,请从图中抽象出一个图形: .(填一个平面图形或一个立体图形即可)?
图6
9.如图7,图中共有 条线段.?
图7
10.如图8,OB平分∠AOC,∠AOD=78°,∠BOC=20°,则∠COD的度数为 .?
图8
11.已知线段AB,C是AB的中点,E是AC的中点,如果AE=2
cm,那么AB= cm.?
12.若∠α的余角与∠α的补角的和是平角,则∠α的度数为 .?
13.(1)8.31°= ° ' ″;?
(2)78°30'36″= °.?
14.如图9,CE平分∠ACD,∠OCE=105°,则∠OCD= °.?
图9
三、解答题(本大题共6小题,共58分)
15.(8分)如图10,写出下列几何体的名称.
图10
16.(8分)计算:
(1)17°15'23″+25°56'18″;
(2)180°-67°28'43″+21°47'13″.
17.(9分)填空,完成下列说理过程:
如图11,∠AOB=90°,∠COD=90°,OA平分∠DOE,若∠BOC=20°,求∠COE的度数.
解:因为∠AOB=90°,
图11
所以∠BOC+ =90°.?
因为∠COD=90°,
所以∠AOD+ =90°.?
所以∠BOC=∠AOD.( )
因为∠BOC=20°,
所以∠AOD=20°.
因为OA平分∠DOE,
所以∠ =2∠AOD= °.( )?
所以∠COE=∠COD-∠DOE= °.?
18.(9分)如图12,D是AB的中点,E是BC的中点,BE=AC=2
cm,求线段DE的长.
图12
19.(12分)如图13,直线AB,CD,EF相交于点O,∠COB=90°,∠AOE∶∠AOC=2∶5,求∠EOC的度数.
图13
20.(12分)如图14,B是线段AD上一动点,沿A→D以2
cm/s的速度运动,C是线段BD的中点,AD=10
cm,设点B运动的时间为t秒.
(1)当t=2时,
①AB= cm;?
②求线段CD的长度.
(2)在运动过程中,若E是AB的中点,则EC的长是否发生变化?若不变,求出EC的长;若发生变化,请说明理由.
图14
教师详解详析
1.D [解析]
选项A中的图形是三棱柱,不符合题意;
选项B中的图形是圆柱,不符合题意;
选项C中的图形是圆锥,不符合题意;
选项D中的图形是四棱锥,符合题意.
故选D.
2.D [解析]
由两个确定的点定线,其数学原理是“两点确定一条直线”.故选D.
3.B [解析]
由正方体四个侧面和上下两个底面的特征可知,A,C,D选项可以拼成一个正方体,而B选项中出现了“凹”字格,不能拼成正方体.
故选B.
4.B
5.A [解析]
因为C是AB的中点,
所以AC=BC.
因为D是BC的中点,所以CD=DB,
所以CD=DB=AB.
故选项A错误.
6.D [解析]
因为OC是∠AOB的平分线,∠AOB=120°,
所以∠COB=∠AOC=∠AOB=60°.
因为OD是∠BOC的平分线,
所以∠COD=∠BOC=30°.
所以∠AOD=∠COD+∠AOC=90°.故选D.
7.D [解析]
135°,75°,120°的角都是15°角的整倍数,可以画出来.25°角不是15°角的整倍数,不能画出来.故选D.
8.答案不唯一,如圆,圆柱,六棱柱等
9.6 [解析]
图中有线段AB,AC,AD,BC,BD,CD,共6条.
10.38° [解析]
因为OB平分∠AOC,∠BOC=20°,
所以∠AOC=40°.
因为∠AOD=78°,所以∠COD=38°.
11.8 [解析]
因为AE=2
cm,E是AC的中点,
所以AC=2AE=2×2=4(cm).
又因为C是AB的中点,
所以AB=2AC=2×4=8(cm).
故答案为8.
12.45°
13.(1)8 18 36 [解析]
因为0.31°=0.31×60'=18.6',0.6×60″=36″,
所以8.31°=8°18'36″.
(2)78.51 [解析]
因为36×'=0.6',
30.6×°=0.51°,
所以78°30'36″=78.51°.
14.30 [解析]
因为∠OCE=105°,
所以∠ACE=180°-105°=75°.
又因为CE平分∠ACD,
所以∠ACD=2∠ACE=150°.
所以∠OCD=30°.
故答案为30.
15.解:从左往右依次为:长方体、球、圆柱、圆锥、六棱柱、四棱锥.
16.解:(1)原式=42°71'41″=43°11'41″.
(2)原式=112°31'17″+21°47'13″=133°78'30″=134°18'30″.
17.∠AOC ∠AOC 同角的余角相等 DOE 40 角平分线的定义 50
18.解:根据题意,得AC=5BE=10
cm.
因为D是AB的中点,E是BC的中点,
所以DE=DB+BE=AB+BC=AC=5
cm.
19.解:因为∠COB=90°,
所以∠AOC=180°-∠COB=90°.
因为∠AOE∶∠AOC=2∶5,
所以∠AOE==36°.
所以∠EOC=90°-36°=54°.
20.解:(1)①4
②因为AD=10
cm,AB=4
cm,
所以BD=10-4=6(cm).
因为C是线段BD的中点,
所以CD=BD=×6=3(cm).
(2)EC的长不变.
因为E是AB的中点,C是BD的中点,
所以EB=AB,BC=BD.
所以EC=EB+BC=(AB+BD)=AD=×10=5(cm).
同课章节目录
