3.1 探索勾股定理 课件(共27张PPT)
文档属性
| 名称 | 3.1 探索勾股定理 课件(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
第三章
勾股定理
1
探索勾股定理
知识点一
勾股定理
勾股定理
文字语言
直角三角形两直角边的平方和等于斜边的平方
符号表示
如果用a,b表示直角边,c表示斜边,那么a2+b2=c2
常见变式
除掌握a2+b2=c2的形式外,还应掌握a2=c2-b2和b2=
c2-a2的形式
图示
?
应用
①已知直角三角形的任意两条边,求第三条边;
②已知直角三角形的一边,求另两边之间的关系;
③用于说明线段平方之间的关系.
温馨提示
(1)勾股定理表示了直角三角形中三边之间的关系.我国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦,故此定理在我国叫做勾股定理.
(2)勾股定理体现了数形结合的思想,即勾股定理把直角三角形中各边之间“形”的关系,转化为各边之间“数”的关系.
(3)在应用勾股定理时,容易出现的错误是把勾股定理记为a2+b2=c2.实际上,a2+b2=c2只适用于当边c所对的角是直角时的情况.
知识点二
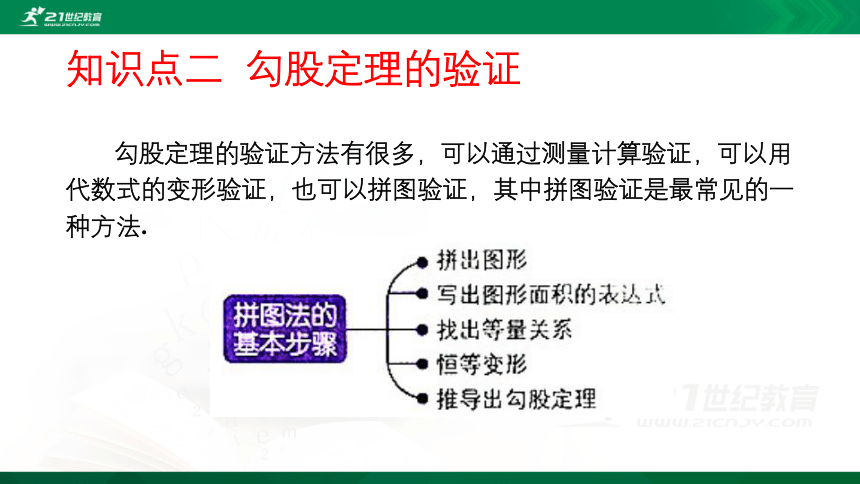
勾股定理的验证
勾股定理的验证方法有很多,可以通过测量计算验证,可以用代数式的变形验证,也可以拼图验证,其中拼图验证是最常见的一种方法.
知识点二
勾股定理的验证
勾股定理的验证方法有很多,可以通过测量计算验证,可以用代数式的变形验证,也可以拼图验证,其中拼图验证是最常见的一种方法.
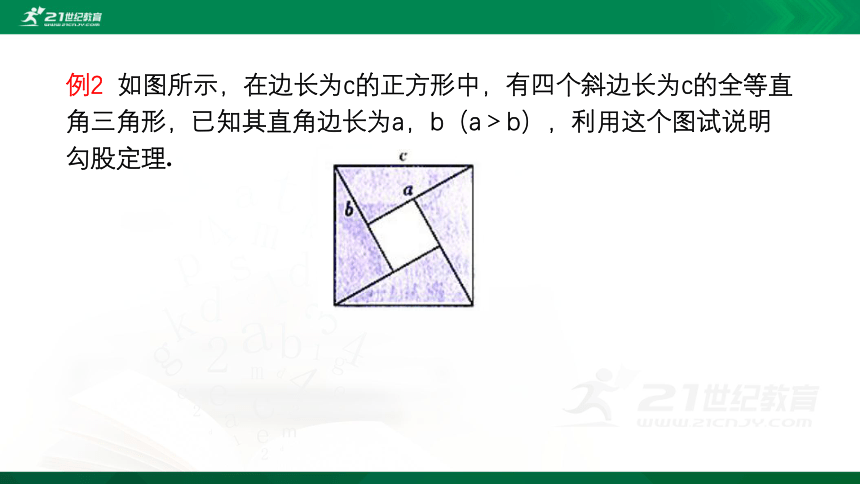
例2
如图所示,在边长为c的正方形中,有四个斜边长为c的全等直角三角形,已知其直角边长为a,b(a>b),利用这个图试说明勾股定理.
知识点三
勾股定理的简单应用
已知直角三角形任意两边的长度,利用勾股定理可以求出第三边的长度.
知识点三
勾股定理的简单应用
已知直角三角形任意两边的长度,利用勾股定理可以求出第三边的长度.
应用勾股定理应注意三个问题:
(1)勾股定理是直角三角形所特有的重要定理之,即应用勾股定理的前提条件是“在直角三角形中”.
(2)应用勾股定理时,要注意分清斜边和直角边,没有明确指明的应进行分类讨论.
(3)不能直接用勾股定理解决问题时,可以添加辅助线构造直角三角形,再根据勾股定理解决.
例3
如图所示,长方形ABCD为一个花园,其中AB=15米,BC=8米,在花园内修一条长13米的笔直小路EF,小路出口一端E选在AD边上距D点3米处,另一端出口F应选在AB边上距B点多少米处?
例3
如图所示,长方形ABCD为一个花园,其中AB=15米,BC=8米,在花园内修一条长13米的笔直小路EF,小路出口一端E选在AD边上距D点3米处,另一端出口F应选在AB边上距B点多少米处?
解析
由题意知EF=13米,EA=5米.
在Rt△EAF中,由勾股定理,得AF2=EF2-EA2,
即AF2=132-52=144,则AF=12(米).
所以FB=15-12=3(米),
即另一端出口F应选在AB边上距B点3米处.
经典例题
题型一
利用勾股定理求图形的面积
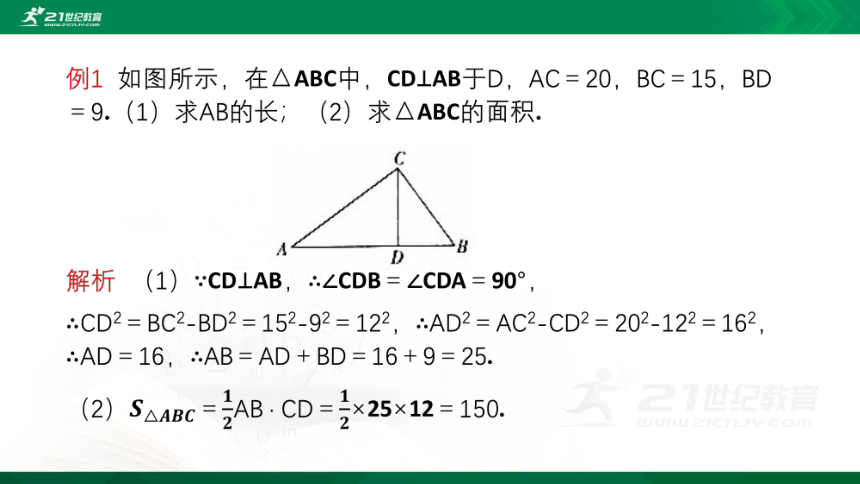
例1
已知:如图所示,分别以Rt△ABC的三边为斜边向外作等腰直角三角形.若AB=3,则图中阴影部分的面积为____________.
拓展延伸
如图①②③,用直角三角形ABC的三条边构造的几种图形(正方形、等边三角形、半圆),均有S1+S2=S3.
题型二
勾股定理在求图形面积中的应用
例2
如图所示,直线l上有三个正方形a,b,c,若a,c的面积分别为7和9,则b的面积为__________.
题型二
勾股定理在求图形面积中的应用
易错易混
易错点一
没有明确哪条边是直角边,哪条边是斜边,盲目求解致错
在应用勾股定理时,若题目没有明确指出哪条边是斜边,哪条边是直角边,则应分情况讨论求解.
例1
若直角三角形的三边长分别为x,8,10,则x2=_________.
例1
若直角三角形的三边长分别为x,8,10,则x2=_________.
解析
分两种情况:①两直角边长分别为8,10,由勾股定理得x2=82+102=164,②一直角边长为8,斜边长为10,由勾股定理得x2=102-82=36.
例1
若直角三角形的三边长分别为x,8,10,则x2=___36____.
解析
分两种情况:①两直角边长分别为8,10,由勾股定理得x2=82+102=164,②一直角边长为8,斜边长为10,由勾股定理得x2=102-82=36.
例1
若直角三角形的三边长分别为x,8,10,则x2=__
36
_____.
解析
分两种情况:①两直角边长分别为8,10,由勾股定理得x2=82+102=164,②一直角边长为8,斜边长为10,由勾股定理得x2=102-82=36.
易错分析
因为没有明确指出10是直角边长还是斜边长,所以要分类讨论此题易误认为10为斜边长,从而漏解.
易错点二
误把一般三角形当作直角三角形
例2
在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,a=3,b=4,b<c,且c为整数,求c的值.
易错点二
误把一般三角形当作直角三角形
例2
在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,a=3,b=4,b<c,且c为整数,求c的值.
解析
因为4-3<c<4+3,即1<c<7,又因为c>b,且c为整数,所以c为5或6.
易错点二
误把一般三角形当作直角三角形
例2
在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,a=3,b=4,b<c,且c为整数,求c的值.
解析
因为4-3<c<4+3,即1<c<7,又因为c>b,且c为整数,所以c为5或6.
易错分析
本题容易思维定式,误以为在直角三角形中,3为勾,4为股,来求斜边长,直接利用“勾三股四弦五”进行求解,从而致错这里题目没有说三角形是直角三角形,所以第三边长无法确定,只能用三边关系结合已知条件求解.
第三章
勾股定理
1
探索勾股定理
知识点一
勾股定理
勾股定理
文字语言
直角三角形两直角边的平方和等于斜边的平方
符号表示
如果用a,b表示直角边,c表示斜边,那么a2+b2=c2
常见变式
除掌握a2+b2=c2的形式外,还应掌握a2=c2-b2和b2=
c2-a2的形式
图示
?
应用
①已知直角三角形的任意两条边,求第三条边;
②已知直角三角形的一边,求另两边之间的关系;
③用于说明线段平方之间的关系.
温馨提示
(1)勾股定理表示了直角三角形中三边之间的关系.我国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦,故此定理在我国叫做勾股定理.
(2)勾股定理体现了数形结合的思想,即勾股定理把直角三角形中各边之间“形”的关系,转化为各边之间“数”的关系.
(3)在应用勾股定理时,容易出现的错误是把勾股定理记为a2+b2=c2.实际上,a2+b2=c2只适用于当边c所对的角是直角时的情况.
知识点二
勾股定理的验证
勾股定理的验证方法有很多,可以通过测量计算验证,可以用代数式的变形验证,也可以拼图验证,其中拼图验证是最常见的一种方法.
知识点二
勾股定理的验证
勾股定理的验证方法有很多,可以通过测量计算验证,可以用代数式的变形验证,也可以拼图验证,其中拼图验证是最常见的一种方法.
例2
如图所示,在边长为c的正方形中,有四个斜边长为c的全等直角三角形,已知其直角边长为a,b(a>b),利用这个图试说明勾股定理.
知识点三
勾股定理的简单应用
已知直角三角形任意两边的长度,利用勾股定理可以求出第三边的长度.
知识点三
勾股定理的简单应用
已知直角三角形任意两边的长度,利用勾股定理可以求出第三边的长度.
应用勾股定理应注意三个问题:
(1)勾股定理是直角三角形所特有的重要定理之,即应用勾股定理的前提条件是“在直角三角形中”.
(2)应用勾股定理时,要注意分清斜边和直角边,没有明确指明的应进行分类讨论.
(3)不能直接用勾股定理解决问题时,可以添加辅助线构造直角三角形,再根据勾股定理解决.
例3
如图所示,长方形ABCD为一个花园,其中AB=15米,BC=8米,在花园内修一条长13米的笔直小路EF,小路出口一端E选在AD边上距D点3米处,另一端出口F应选在AB边上距B点多少米处?
例3
如图所示,长方形ABCD为一个花园,其中AB=15米,BC=8米,在花园内修一条长13米的笔直小路EF,小路出口一端E选在AD边上距D点3米处,另一端出口F应选在AB边上距B点多少米处?
解析
由题意知EF=13米,EA=5米.
在Rt△EAF中,由勾股定理,得AF2=EF2-EA2,
即AF2=132-52=144,则AF=12(米).
所以FB=15-12=3(米),
即另一端出口F应选在AB边上距B点3米处.
经典例题
题型一
利用勾股定理求图形的面积
例1
已知:如图所示,分别以Rt△ABC的三边为斜边向外作等腰直角三角形.若AB=3,则图中阴影部分的面积为____________.
拓展延伸
如图①②③,用直角三角形ABC的三条边构造的几种图形(正方形、等边三角形、半圆),均有S1+S2=S3.
题型二
勾股定理在求图形面积中的应用
例2
如图所示,直线l上有三个正方形a,b,c,若a,c的面积分别为7和9,则b的面积为__________.
题型二
勾股定理在求图形面积中的应用
易错易混
易错点一
没有明确哪条边是直角边,哪条边是斜边,盲目求解致错
在应用勾股定理时,若题目没有明确指出哪条边是斜边,哪条边是直角边,则应分情况讨论求解.
例1
若直角三角形的三边长分别为x,8,10,则x2=_________.
例1
若直角三角形的三边长分别为x,8,10,则x2=_________.
解析
分两种情况:①两直角边长分别为8,10,由勾股定理得x2=82+102=164,②一直角边长为8,斜边长为10,由勾股定理得x2=102-82=36.
例1
若直角三角形的三边长分别为x,8,10,则x2=___36____.
解析
分两种情况:①两直角边长分别为8,10,由勾股定理得x2=82+102=164,②一直角边长为8,斜边长为10,由勾股定理得x2=102-82=36.
例1
若直角三角形的三边长分别为x,8,10,则x2=__
36
_____.
解析
分两种情况:①两直角边长分别为8,10,由勾股定理得x2=82+102=164,②一直角边长为8,斜边长为10,由勾股定理得x2=102-82=36.
易错分析
因为没有明确指出10是直角边长还是斜边长,所以要分类讨论此题易误认为10为斜边长,从而漏解.
易错点二
误把一般三角形当作直角三角形
例2
在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,a=3,b=4,b<c,且c为整数,求c的值.
易错点二
误把一般三角形当作直角三角形
例2
在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,a=3,b=4,b<c,且c为整数,求c的值.
解析
因为4-3<c<4+3,即1<c<7,又因为c>b,且c为整数,所以c为5或6.
易错点二
误把一般三角形当作直角三角形
例2
在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,a=3,b=4,b<c,且c为整数,求c的值.
解析
因为4-3<c<4+3,即1<c<7,又因为c>b,且c为整数,所以c为5或6.
易错分析
本题容易思维定式,误以为在直角三角形中,3为勾,4为股,来求斜边长,直接利用“勾三股四弦五”进行求解,从而致错这里题目没有说三角形是直角三角形,所以第三边长无法确定,只能用三边关系结合已知条件求解.
