22.4 第1课时 位似图形的概念与性质 同步课时作业 2021-2022学年九年级数学沪科版上册(Word版含答案)
文档属性
| 名称 | 22.4 第1课时 位似图形的概念与性质 同步课时作业 2021-2022学年九年级数学沪科版上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 262.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 00:00:00 | ||
图片预览



文档简介
22.4 第1课时 位似图形的概念与性质
知识点
1 位似图形的概念
1.图1中的两个相似三角形不是位似图形的是
( )
图1
2.如图2,已知BC∥DE,则下列说法中不正确的是( )
图2
A.两个三角形是位似图形
B.点A是两个三角形的位似中心
C.点B与点D,点C与点E分别是对应点
D.AE∶AD是相似比
3.如图3,点O是等边三角形PQR的中心,P',Q',R'分别是OP,OQ,OR的中点,则△P'Q'R'与△PQR是位似三角形,此时△P'Q'R'与△PQR的相似比、位似中心分别是
( )
图3
A.2、点P
B.、点P
C.2、点O
D.、点O
4.已知△ABC与△A1B1C1位似,△ABC与△A2B2C2位似,则
( )
A.△A1B1C1与△A2B2C2全等
B.△A1B1C1与△A2B2C2位似
C.△A1B1C1与△A2B2C2相似但不一定位似
D.△A1B1C1与△A2B2C2不相似
知识点
2 位似图形的性质
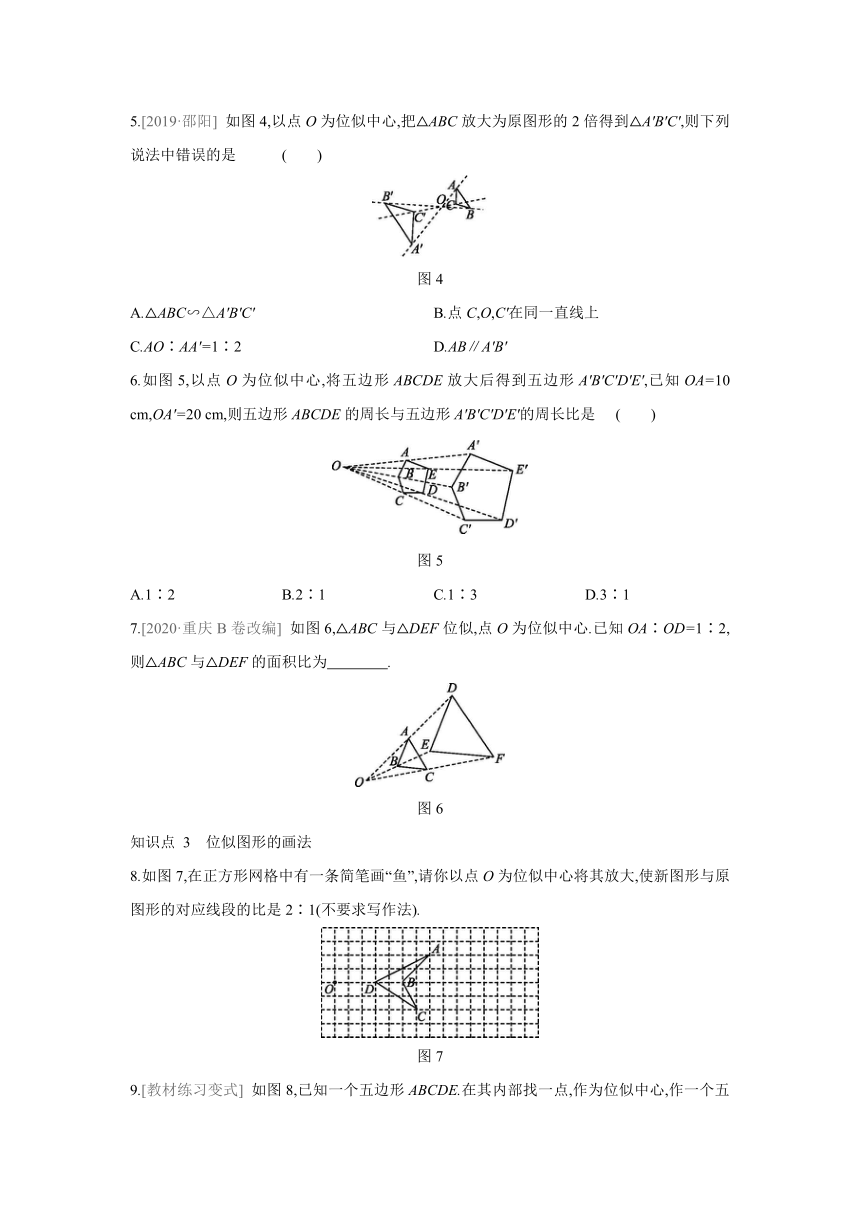
5.[2019·邵阳]
如图4,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',则下列说法中错误的是
( )
图4
A.△ABC∽△A'B'C'
B.点C,O,C'在同一直线上
C.AO∶AA'=1∶2
D.AB∥A'B'
6.如图5,以点O为位似中心,将五边形ABCDE放大后得到五边形A'B'C'D'E',已知OA=10
cm,OA'=20
cm,则五边形ABCDE的周长与五边形A'B'C'D'E'的周长比是
( )
图5
A.1∶2
B.2∶1
C.1∶3
D.3∶1
7.[2020·重庆B卷改编]
如图6,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为 .?
图6
知识点
3 位似图形的画法
8.如图7,在正方形网格中有一条简笔画“鱼”,请你以点O为位似中心将其放大,使新图形与原图形的对应线段的比是2∶1(不要求写作法).
图7
9.[教材练习变式]
如图8,已知一个五边形ABCDE.在其内部找一点,作为位似中心,作一个五边形使它和原五边形位似,且相似比为1∶2.
图8
10.如图9,四边形ABCD的周长为12
cm,它的位似图形为四边形A'B'C'D',位似中心为点O.若OA∶AA'=1∶3,则四边形A'B'C'D'的周长为
( )
图9
A.12
cm
B.24
cm
C.12
cm或24
cm
D.以上都不对
11.如图10,若=
==,有下列说法:
图10
①△ABC与△DEF是相似图形;②△ABC与△DEF的周长之比是;③△ABC与△DEF是位似图形;④△DEF与△ABC的面积之比是4∶1.其中正确的有
( )
A.1个
B.2个
C.3个
D.4个
12.[2019·宣城期末]
图11中的小方格是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出点O;
(2)求出△ABC与△A'B'C'的相似比;
(3)将△ABC向右平移4个单位,再向上平移6个单位,得到△A2B2C2,请在图中画出△A2B2C2.
图11
13.如图12,点F在BD上,BC,AD相交于点E,且AB∥CD∥EF.
(1)图中有哪几对位似三角形?
(2)选其中一对加以证明.
图12
14.在数学活动中,林老师给出如下的操作步骤:如图13(a),①在△AOB内画任意等边三角形CDE,使点C在OA上,点D在OB上;②连接OE并延长,交AB于点E',过点E'作C'E'∥CE,交OA于点C',作D'E'∥DE,交OB于点D',并连接C'D'.林老师告诉同学们△C'D'E'是△AOB的内接等边三角形.
(1)请证明林老师的结论.
(2)①仿照林老师的操作步骤,请在图(b)中作出△AOB的内接正方形CDEF,要求DE边与OB边重合,点C,F分别在OA,AB上;(不需要写作图过程,画出图形即可)
②若OB=10,OA=8,AB=6,求内接正方形CDEF的边长.
图13
教师详解详析
1.D [解析]
对应顶点的连线相交于一点的两个相似多边形叫做位似图形.根据位似图形的概念,A,B,C三个选项中的两个图形都是位似图形.D项中的两个相似三角形,顶点A与D对应,B与E对应,对应顶点的连线不能相交于一点,不符合位似图形的概念,故不是位似图形.故选D.
2.D [解析]
相似比等于这两个三角形的对应边的比,即AE∶AC或AD∶AB或DE∶BC是相似比.
3.D 4.C
5.C [解析]
∵以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',∴△ABC∽△A'B'C',点C,O,C'在同一直线上,AB∥A'B',AO∶OA'=1∶2,故选项C错误,符合题意.故选C.
6.A [解析]
∵OA=10
cm,OA'=20
cm,∴五边形ABCDE与五边形A'B'C'D'E'的相似比=10∶20=1∶2,
∴五边形ABCDE的周长与五边形A'B'C'D'E'的周长比是1∶2.
故选A.
7.1∶4 [解析]
∵△ABC与△DEF位似,且=,∴=()2=.
8.解:连接OA,OB,OC,OD并延长到点A',B',C',D',使OA',OB',OC',OD'的长度分别是OA,OB,OC,OD长度的2倍,再顺次连接各点.图略.
9.解:如图,在五边形ABCDE内部任找一点O,连接OA,OB,OC,OD,OE,然后在OA上取OA'=OA,在OB上取OB'=OB,在OC上取OC'=OC,在OD上取OD'=OD,在OE上取OE'=OE,顺次连接A',B',C',D',E',得到的五边形即为所求.
10.B
11.D
12.解:(1)如图:
(2)△ABC与△A'B'C'的相似比为OA∶OA'=6∶12=1∶2.
(3)如图.
13.解:(1)∵AB∥CD∥EF,
∴△DFE与△DBA,△BFE与△BDC,△AEB与△DEC都是位似三角形,一共有3对.
(2)证明:∵AB∥CD∥EF,
∴△DFE∽△DBA,△BFE∽△BDC,△AEB∽△DEC,且对应点的连线都交于一点,
∴△DFE与△DBA,△BFE与△BDC,△AEB与△DEC都是位似三角形.(答案不唯一,选择其中一对证明即可)
14.解:(1)证明:∵C'E'∥CE,D'E'∥DE,
∴=,=,
∠CEO=∠C'E'O,∠DEO=∠D'E'O,
∴=,∠CED=∠C'E'D',
∴△CDE∽△C'D'E'.
又∵△CDE是等边三角形,
∴△C'D'E'是等边三角形.
∵点C',D',E'分别在OA,OB,AB上,
∴△C'D'E'是△AOB的内接等边三角形.
(2)①如图,正方形CDEF即为所求.
②如图,过点A作AH⊥OB于点H,与CF交于点G,则AG⊥CF.
设CF=x,则GH=x.
∵OB=10,OA=8,AB=6,
∴△AOB是直角三角形,
∴S△AOB=OA·AB=AH·OB,
则AH===.
∵CF∥OB,∴△ACF∽△AOB,
∴=,即=,
解得x=.
故内接正方形CDEF的边长为.
知识点
1 位似图形的概念
1.图1中的两个相似三角形不是位似图形的是
( )
图1
2.如图2,已知BC∥DE,则下列说法中不正确的是( )
图2
A.两个三角形是位似图形
B.点A是两个三角形的位似中心
C.点B与点D,点C与点E分别是对应点
D.AE∶AD是相似比
3.如图3,点O是等边三角形PQR的中心,P',Q',R'分别是OP,OQ,OR的中点,则△P'Q'R'与△PQR是位似三角形,此时△P'Q'R'与△PQR的相似比、位似中心分别是
( )
图3
A.2、点P
B.、点P
C.2、点O
D.、点O
4.已知△ABC与△A1B1C1位似,△ABC与△A2B2C2位似,则
( )
A.△A1B1C1与△A2B2C2全等
B.△A1B1C1与△A2B2C2位似
C.△A1B1C1与△A2B2C2相似但不一定位似
D.△A1B1C1与△A2B2C2不相似
知识点
2 位似图形的性质
5.[2019·邵阳]
如图4,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',则下列说法中错误的是
( )
图4
A.△ABC∽△A'B'C'
B.点C,O,C'在同一直线上
C.AO∶AA'=1∶2
D.AB∥A'B'
6.如图5,以点O为位似中心,将五边形ABCDE放大后得到五边形A'B'C'D'E',已知OA=10
cm,OA'=20
cm,则五边形ABCDE的周长与五边形A'B'C'D'E'的周长比是
( )
图5
A.1∶2
B.2∶1
C.1∶3
D.3∶1
7.[2020·重庆B卷改编]
如图6,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为 .?
图6
知识点
3 位似图形的画法
8.如图7,在正方形网格中有一条简笔画“鱼”,请你以点O为位似中心将其放大,使新图形与原图形的对应线段的比是2∶1(不要求写作法).
图7
9.[教材练习变式]
如图8,已知一个五边形ABCDE.在其内部找一点,作为位似中心,作一个五边形使它和原五边形位似,且相似比为1∶2.
图8
10.如图9,四边形ABCD的周长为12
cm,它的位似图形为四边形A'B'C'D',位似中心为点O.若OA∶AA'=1∶3,则四边形A'B'C'D'的周长为
( )
图9
A.12
cm
B.24
cm
C.12
cm或24
cm
D.以上都不对
11.如图10,若=
==,有下列说法:
图10
①△ABC与△DEF是相似图形;②△ABC与△DEF的周长之比是;③△ABC与△DEF是位似图形;④△DEF与△ABC的面积之比是4∶1.其中正确的有
( )
A.1个
B.2个
C.3个
D.4个
12.[2019·宣城期末]
图11中的小方格是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出点O;
(2)求出△ABC与△A'B'C'的相似比;
(3)将△ABC向右平移4个单位,再向上平移6个单位,得到△A2B2C2,请在图中画出△A2B2C2.
图11
13.如图12,点F在BD上,BC,AD相交于点E,且AB∥CD∥EF.
(1)图中有哪几对位似三角形?
(2)选其中一对加以证明.
图12
14.在数学活动中,林老师给出如下的操作步骤:如图13(a),①在△AOB内画任意等边三角形CDE,使点C在OA上,点D在OB上;②连接OE并延长,交AB于点E',过点E'作C'E'∥CE,交OA于点C',作D'E'∥DE,交OB于点D',并连接C'D'.林老师告诉同学们△C'D'E'是△AOB的内接等边三角形.
(1)请证明林老师的结论.
(2)①仿照林老师的操作步骤,请在图(b)中作出△AOB的内接正方形CDEF,要求DE边与OB边重合,点C,F分别在OA,AB上;(不需要写作图过程,画出图形即可)
②若OB=10,OA=8,AB=6,求内接正方形CDEF的边长.
图13
教师详解详析
1.D [解析]
对应顶点的连线相交于一点的两个相似多边形叫做位似图形.根据位似图形的概念,A,B,C三个选项中的两个图形都是位似图形.D项中的两个相似三角形,顶点A与D对应,B与E对应,对应顶点的连线不能相交于一点,不符合位似图形的概念,故不是位似图形.故选D.
2.D [解析]
相似比等于这两个三角形的对应边的比,即AE∶AC或AD∶AB或DE∶BC是相似比.
3.D 4.C
5.C [解析]
∵以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',∴△ABC∽△A'B'C',点C,O,C'在同一直线上,AB∥A'B',AO∶OA'=1∶2,故选项C错误,符合题意.故选C.
6.A [解析]
∵OA=10
cm,OA'=20
cm,∴五边形ABCDE与五边形A'B'C'D'E'的相似比=10∶20=1∶2,
∴五边形ABCDE的周长与五边形A'B'C'D'E'的周长比是1∶2.
故选A.
7.1∶4 [解析]
∵△ABC与△DEF位似,且=,∴=()2=.
8.解:连接OA,OB,OC,OD并延长到点A',B',C',D',使OA',OB',OC',OD'的长度分别是OA,OB,OC,OD长度的2倍,再顺次连接各点.图略.
9.解:如图,在五边形ABCDE内部任找一点O,连接OA,OB,OC,OD,OE,然后在OA上取OA'=OA,在OB上取OB'=OB,在OC上取OC'=OC,在OD上取OD'=OD,在OE上取OE'=OE,顺次连接A',B',C',D',E',得到的五边形即为所求.
10.B
11.D
12.解:(1)如图:
(2)△ABC与△A'B'C'的相似比为OA∶OA'=6∶12=1∶2.
(3)如图.
13.解:(1)∵AB∥CD∥EF,
∴△DFE与△DBA,△BFE与△BDC,△AEB与△DEC都是位似三角形,一共有3对.
(2)证明:∵AB∥CD∥EF,
∴△DFE∽△DBA,△BFE∽△BDC,△AEB∽△DEC,且对应点的连线都交于一点,
∴△DFE与△DBA,△BFE与△BDC,△AEB与△DEC都是位似三角形.(答案不唯一,选择其中一对证明即可)
14.解:(1)证明:∵C'E'∥CE,D'E'∥DE,
∴=,=,
∠CEO=∠C'E'O,∠DEO=∠D'E'O,
∴=,∠CED=∠C'E'D',
∴△CDE∽△C'D'E'.
又∵△CDE是等边三角形,
∴△C'D'E'是等边三角形.
∵点C',D',E'分别在OA,OB,AB上,
∴△C'D'E'是△AOB的内接等边三角形.
(2)①如图,正方形CDEF即为所求.
②如图,过点A作AH⊥OB于点H,与CF交于点G,则AG⊥CF.
设CF=x,则GH=x.
∵OB=10,OA=8,AB=6,
∴△AOB是直角三角形,
∴S△AOB=OA·AB=AH·OB,
则AH===.
∵CF∥OB,∴△ACF∽△AOB,
∴=,即=,
解得x=.
故内接正方形CDEF的边长为.
