2021-2022学年沪科版九年级数学上册第21-23章:阶段测试(Word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版九年级数学上册第21-23章:阶段测试(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 269.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 09:37:35 | ||
图片预览




文档简介
阶段测试(四)
[范围:第21
~23章 时间:120分钟 分值:150分]
一、选择题(本大题共10小题,每小题4分,满分40分)
1.计算2sin30°的值为
( )
A.1
B.
C.2
D.2
2.将函数y=-2x2的图象先向右平移1个单位,再向下平移2个单位,所得函数图象的表达式是
( )
A.y=-2(x-1)2+2
B.y=-2(x-1)2-2
C.y=-2(x+1)2+2
D.y=-2(x+1)2-2
3.若双曲线y=在每一个象限内,y随x的增大而减小,则k的取值范围是
( )
A.k≠3
B.k<3
C.k≥3
D.k>3
4.如果两个相似三角形的面积比是4∶9,那么它们对应边上的中线之比为
( )
A.4∶9
B.9∶4
C.3∶2
D.2∶3
5.锐角α在正方形网格中的位置如图1所示,则sinα的值为
( )
图1
A.
B.
C.
D.
6.如图2,已知直线a∥b∥c,直线AC,DF与a,b,c相交,且AB=6,BC=4,DE=,则EF的长为
( )
图2
A.
B.
C.
D.3
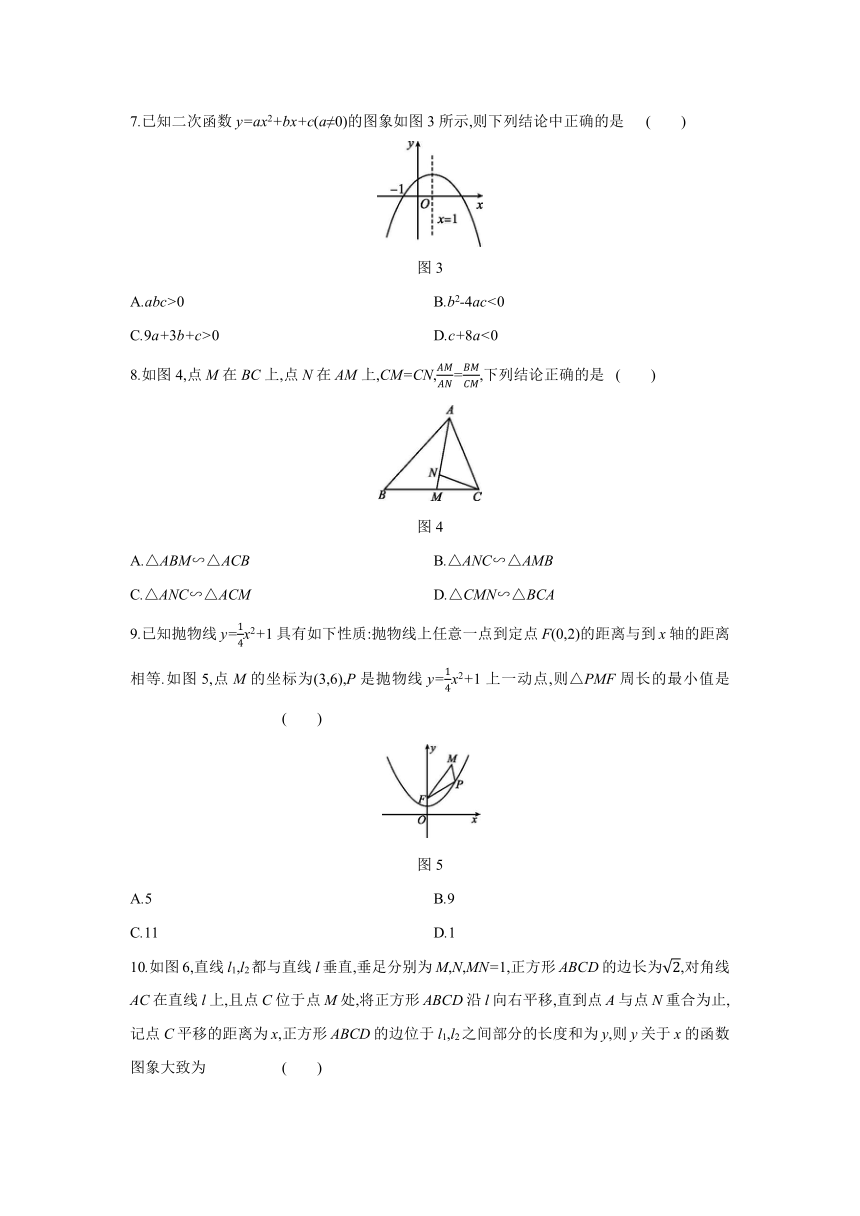
7.已知二次函数y=ax2+bx+c(a≠0)的图象如图3所示,则下列结论中正确的是
( )
图3
A.abc>0
B.b2-4ac<0
C.9a+3b+c>0
D.c+8a<0
8.如图4,点M在BC上,点N在AM上,CM=CN,=,下列结论正确的是
( )
图4
A.△ABM∽△ACB
B.△ANC∽△AMB
C.△ANC∽△ACM
D.△CMN∽△BCA
9.已知抛物线y=x2+1具有如下性质:抛物线上任意一点到定点F(0,2)的距离与到x轴的距离相等.如图5,点M的坐标为(3,6),P是抛物线y=x2+1上一动点,则△PMF周长的最小值是
( )
图5
A.5
B.9
C.11
D.1
10.如图6,直线l1,l2都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于l1,l2之间部分的长度和为y,则y关于x的函数图象大致为
( )
图6
图7
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如果=,那么= .?
12.在Rt△ABC中,∠C=90°,BC=5,AB=10,那么∠B= °.?
13.已知二次函数y=(a+1)x2-x+a2-1的图象经过原点,则a的值是 .?
14.如图8,Rt△ABC中,∠ACB=90°,BC=6,D是BC的中点,CE⊥AD于点E.
图8
(1)DE·AD的值为 ;?
(2)若∠CAB=40°,则∠BED的大小为 .?
三、(本大题共2小题,每小题8分,满分16分)
15.计算:2cos30°-2sin45°+3tan60°+|1-|.
16.如图9,已知O是坐标原点,A,B两点的坐标分别为(3,-1),(2,1).
(1)以点O为位似中心,在y轴的左侧将△OAB放大2倍,画出△OA'B'(点A的对应点为点A',点B的对应点为点B');
(2)分别写出(1)中A,B两点的对应点A',B'的坐标.
图9
四、(本大题共2小题,每小题8分,满分16分)
17.已知二次函数的图象经过点(0,-3),且顶点坐标为(-1,-4).
(1)求该二次函数的表达式;
(2)设该二次函数的图象与x轴的交点为A,B,与y轴的交点为C,求△ABC的面积.
18.如图10,为了测量白塔的高度AB,在D处用高为1.5米的测角仪CD,测得塔顶A的仰角为42°,再向白塔方向前进12米到达点H,又测得塔顶A的仰角为61°,求白塔的高度AB.(结果保留整数.参考数据:sin42°≈0.67,tan42°≈0.90,sin61°≈0.87,tan61°≈1.80)
图10
五、(本大题共2小题,每小题10分,满分20分)
19.如图11,在四边形ABCD中,AC平分∠DAB,AC2=AB·AD,∠ADC=90°,E为AB的中点,DE交AC于点F.
(1)求证:△ADC∽△ACB;
(2)若AD=2,AB=3,求的值.
图11
20.如图12,函数y1=k1x+b的图象与y2=(x>0)的图象交于点A(2,1)和点B,交y轴于点C(0,3).
(1)求函数y1与y2的表达式及点B的坐标;
(2)观察图象,比较当x>0时,y1与y2的大小.
图12
六、(本题满分12分)
21.2020年某市猪肉售价逐月上涨,每千克猪肉的售价y1(元)与月份x(2≤x≤12,且x为整数)之间满足一次函数关系y1=2x+6.每千克猪肉的成本y2(元)与月份x(2≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,5月份成本为10元.
(1)求y2与x之间的函数表达式;
(2)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数表达式,哪个月份销售每千克猪肉所获的利润最大?最大利润是多少元?
七、(本题满分12分)
22.如图13,在△ABC中,AB=AC=13,BC=10,AG⊥BC于点G,D是BC上的点,DE⊥AB于点E,DF∥AB交AC于点F.
(1)求证:△DBE∽△ABG;
(2)当△DEF的面积最大时,求BD的长.
图13
八、(本题满分14分)
23.如图14①,矩形ABCD中,AB=a,BC=b,点M,N分别在边AB,CD上,点E,F分别在边BC,AD上.MN,EF交于点P,记k=
MN∶EF.
(1)如图②,若a∶b的值为1,当MN⊥EF时,求k的值;
(2)若k的值为3,当N是矩形的顶点,∠MPE=60°,MP=EF=3PE时,求a∶b的值.
图14
教师详解详析
1.A 2.B 3.D 4.D 5.B
6.C 7.D 8.B 9.C 10.A 11. 12.30 13.1
14.(1)9 (2)50°
[解析]
(1)∵CE⊥AD,
∴∠CED=∠ACB=90°.
又∵∠CDE=∠ADC,∴△CDE∽△ADC,
∴CD∶AD=DE∶CD,
∴CD2=DE·AD.
∵BC=6,D是BC的中点,
∴DE·AD=32=9.
(2)∵CD2=DE·AD,BD=CD,
∴BD2=DE·AD,
∴BD∶AD=DE∶BD.
又∵∠ADB=∠BDE,∴△ADB∽△BDE,
∴∠BED=∠ABD=90°-40°=50°.
15.解:原式=2×-2×+3+-1
2分
=-+3+-1
4分
=4-1.
8分
16.解:(1)如图所示,△OA'B'即为所求.
4分
(2)点A'的坐标是(-6,2),点B'的坐标是(-4,-2).
8分
17.解:(1)设二次函数的表达式为y=a(x+1)2-4.
1分
∵图象经过点(0,-3).
∴a-4=-3,解得a=1.
2分
∴二次函数的表达式为y=(x+1)2-4.
4分
(2)当y=0时,(x+1)2-4=0,
解得x1=1,x2=-3,
∴AB=4.
又∵C(0,-3),
∴OC=3,
∴S△ABC=AB·OC=×4×3=6.
8分
18.解:如图,过点C作CE⊥AB于点E.设AE=x.
在Rt△ACE中,CE=≈1.11x.
2分
在Rt△AFE中,FE=≈0.56x.
4分
由题意,得CF=CE-FE≈1.11x-0.56x=12,
解得x≈21.82.
6分
故AB=AE+BE≈21.82+1.5≈23(米).
答:白塔的高度AB约为23米.
8分
19.解:(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB.
2分
∵AC2=AB·AD,
∴=,
∴△ADC∽△ACB.
4分
(2)∵△ADC∽△ACB,
∴∠ACB=∠ADC=90°.
6分
∵E为AB的中点,
∴CE=AE=AB=,
∴∠EAC=∠ECA.
∵∠DAC=∠EAC,
∴∠DAC=∠ECA,
∴CE∥AD.
8分
∴==,
∴=.
10分
20.解:(1)把点A(2,1)代入y2=,得k2=2,
∴y2=.
把点A(2,1),点C(0,3)代入y1=k1x+b,得解得
∴y1=-x+3.
3分
令y1=y2,即-x+3=,解得x1=2,x2=1,经检验x1=2,x2=1均为原方程的解.
由题意可知x1=2应舍去,
∴点B的坐标为(1,2).
6分
(2)观察图象可得当02时,y1当1y2;
当x=1或x=2时,y1=y2.
10分
21.解:(1)由题意,得抛物线的顶点坐标为(3,9),且经过点(5,10).
设y2与x之间的函数表达式为y2=a(x-3)2+9.
2分
将(5,10)代入y2=a(x-3)2+9,得a(5-3)2+9=10,解得a=,
∴y2与x之间的函数表达式为y2=(x-3)2+9=x2-x+.
6分
(2)由题意,得
w=y1-y2=2x+6-(x2-x+)
=-x2+x-
=-(x-7)2+7.
∴当x=7时,w取得最大值7.
∴7月份销售每千克猪肉所获的利润最大,最大利润是7元.
12分
22.解:(1)证明:∵DE⊥AB,AG⊥BC,
∴∠BED=∠BGA=90°.
∵∠B=∠B,
∴△DBE∽△ABG.
4分
(2)∵BC=10,AB=AC=13,∴BG=5,
∴AG=12.
设BD=x,则CD=10-x.
∵△DBE∽△ABG,∴=,
∴ED=x.
∵DF∥AB,
∴∠EDF=∠BED=90°,=,
∴DF=1.3(10-x),
∴△DEF的面积=×x×1.3(10-x)
8分
=0.6x(10-x)
=-0.6(x-5)2+15.
∴当△DEF的面积最大时,x=5,即BD的长为5.
12分
23.解:(1)如图①,作FH⊥BC于点H,MQ⊥CD于点Q.
∵四边形ABCD是正方形,FH=AB,MQ=BC,
∴FH=MQ.
∵EF⊥MN,
∴∠EPN=90°.
∵∠ECN=90°,
∴∠MNQ+∠CEP=180°.
∵∠FEH+∠CEP=180°,
∴∠FEH=∠MNQ.
又∵∠EHF=∠NQM=90°,
∴△FHE≌△MQN,
4分
∴MN=EF,
∴k=MN∶EF=1.
6分
(2)连接FN,ME.
∵k=3,MP=EF=3PE,
∴===3,∴==2.
又∠FPN=∠EPM,∴△PNF∽△PME,
∴==2,∠FNP=∠EMP,
∴ME∥NF.
9分
设PE=2m,则PF=4m,MP=6m,PN=12m.
①如图②,当点N与点D重合时,点M恰好与点B重合.作FH⊥BD于点H.
∵∠MPE=∠FPH=60°,PF=4m,
∴PH=2m,FH=2m,
∴DH=PN-PH=10m,
∴==tan∠ADB==.
11分
②如图③,当点N与点C重合时,作EH⊥MN于点H,则易得PH=m,HE=m,
∴HC=PH+PN=13m.
∴tan∠HCE===.
∵ME∥NF,AD∥BC,
∴∠MEB=∠FNB=∠NFD.
∵∠B=∠D,
∴△MEB∽△NFD.
∴==2,
∴===.综上所述,a∶b的值为或.
14分
[范围:第21
~23章 时间:120分钟 分值:150分]
一、选择题(本大题共10小题,每小题4分,满分40分)
1.计算2sin30°的值为
( )
A.1
B.
C.2
D.2
2.将函数y=-2x2的图象先向右平移1个单位,再向下平移2个单位,所得函数图象的表达式是
( )
A.y=-2(x-1)2+2
B.y=-2(x-1)2-2
C.y=-2(x+1)2+2
D.y=-2(x+1)2-2
3.若双曲线y=在每一个象限内,y随x的增大而减小,则k的取值范围是
( )
A.k≠3
B.k<3
C.k≥3
D.k>3
4.如果两个相似三角形的面积比是4∶9,那么它们对应边上的中线之比为
( )
A.4∶9
B.9∶4
C.3∶2
D.2∶3
5.锐角α在正方形网格中的位置如图1所示,则sinα的值为
( )
图1
A.
B.
C.
D.
6.如图2,已知直线a∥b∥c,直线AC,DF与a,b,c相交,且AB=6,BC=4,DE=,则EF的长为
( )
图2
A.
B.
C.
D.3
7.已知二次函数y=ax2+bx+c(a≠0)的图象如图3所示,则下列结论中正确的是
( )
图3
A.abc>0
B.b2-4ac<0
C.9a+3b+c>0
D.c+8a<0
8.如图4,点M在BC上,点N在AM上,CM=CN,=,下列结论正确的是
( )
图4
A.△ABM∽△ACB
B.△ANC∽△AMB
C.△ANC∽△ACM
D.△CMN∽△BCA
9.已知抛物线y=x2+1具有如下性质:抛物线上任意一点到定点F(0,2)的距离与到x轴的距离相等.如图5,点M的坐标为(3,6),P是抛物线y=x2+1上一动点,则△PMF周长的最小值是
( )
图5
A.5
B.9
C.11
D.1
10.如图6,直线l1,l2都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于l1,l2之间部分的长度和为y,则y关于x的函数图象大致为
( )
图6
图7
二、填空题(本大题共4小题,每小题5分,满分20分)
11.如果=,那么= .?
12.在Rt△ABC中,∠C=90°,BC=5,AB=10,那么∠B= °.?
13.已知二次函数y=(a+1)x2-x+a2-1的图象经过原点,则a的值是 .?
14.如图8,Rt△ABC中,∠ACB=90°,BC=6,D是BC的中点,CE⊥AD于点E.
图8
(1)DE·AD的值为 ;?
(2)若∠CAB=40°,则∠BED的大小为 .?
三、(本大题共2小题,每小题8分,满分16分)
15.计算:2cos30°-2sin45°+3tan60°+|1-|.
16.如图9,已知O是坐标原点,A,B两点的坐标分别为(3,-1),(2,1).
(1)以点O为位似中心,在y轴的左侧将△OAB放大2倍,画出△OA'B'(点A的对应点为点A',点B的对应点为点B');
(2)分别写出(1)中A,B两点的对应点A',B'的坐标.
图9
四、(本大题共2小题,每小题8分,满分16分)
17.已知二次函数的图象经过点(0,-3),且顶点坐标为(-1,-4).
(1)求该二次函数的表达式;
(2)设该二次函数的图象与x轴的交点为A,B,与y轴的交点为C,求△ABC的面积.
18.如图10,为了测量白塔的高度AB,在D处用高为1.5米的测角仪CD,测得塔顶A的仰角为42°,再向白塔方向前进12米到达点H,又测得塔顶A的仰角为61°,求白塔的高度AB.(结果保留整数.参考数据:sin42°≈0.67,tan42°≈0.90,sin61°≈0.87,tan61°≈1.80)
图10
五、(本大题共2小题,每小题10分,满分20分)
19.如图11,在四边形ABCD中,AC平分∠DAB,AC2=AB·AD,∠ADC=90°,E为AB的中点,DE交AC于点F.
(1)求证:△ADC∽△ACB;
(2)若AD=2,AB=3,求的值.
图11
20.如图12,函数y1=k1x+b的图象与y2=(x>0)的图象交于点A(2,1)和点B,交y轴于点C(0,3).
(1)求函数y1与y2的表达式及点B的坐标;
(2)观察图象,比较当x>0时,y1与y2的大小.
图12
六、(本题满分12分)
21.2020年某市猪肉售价逐月上涨,每千克猪肉的售价y1(元)与月份x(2≤x≤12,且x为整数)之间满足一次函数关系y1=2x+6.每千克猪肉的成本y2(元)与月份x(2≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,5月份成本为10元.
(1)求y2与x之间的函数表达式;
(2)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数表达式,哪个月份销售每千克猪肉所获的利润最大?最大利润是多少元?
七、(本题满分12分)
22.如图13,在△ABC中,AB=AC=13,BC=10,AG⊥BC于点G,D是BC上的点,DE⊥AB于点E,DF∥AB交AC于点F.
(1)求证:△DBE∽△ABG;
(2)当△DEF的面积最大时,求BD的长.
图13
八、(本题满分14分)
23.如图14①,矩形ABCD中,AB=a,BC=b,点M,N分别在边AB,CD上,点E,F分别在边BC,AD上.MN,EF交于点P,记k=
MN∶EF.
(1)如图②,若a∶b的值为1,当MN⊥EF时,求k的值;
(2)若k的值为3,当N是矩形的顶点,∠MPE=60°,MP=EF=3PE时,求a∶b的值.
图14
教师详解详析
1.A 2.B 3.D 4.D 5.B
6.C 7.D 8.B 9.C 10.A 11. 12.30 13.1
14.(1)9 (2)50°
[解析]
(1)∵CE⊥AD,
∴∠CED=∠ACB=90°.
又∵∠CDE=∠ADC,∴△CDE∽△ADC,
∴CD∶AD=DE∶CD,
∴CD2=DE·AD.
∵BC=6,D是BC的中点,
∴DE·AD=32=9.
(2)∵CD2=DE·AD,BD=CD,
∴BD2=DE·AD,
∴BD∶AD=DE∶BD.
又∵∠ADB=∠BDE,∴△ADB∽△BDE,
∴∠BED=∠ABD=90°-40°=50°.
15.解:原式=2×-2×+3+-1
2分
=-+3+-1
4分
=4-1.
8分
16.解:(1)如图所示,△OA'B'即为所求.
4分
(2)点A'的坐标是(-6,2),点B'的坐标是(-4,-2).
8分
17.解:(1)设二次函数的表达式为y=a(x+1)2-4.
1分
∵图象经过点(0,-3).
∴a-4=-3,解得a=1.
2分
∴二次函数的表达式为y=(x+1)2-4.
4分
(2)当y=0时,(x+1)2-4=0,
解得x1=1,x2=-3,
∴AB=4.
又∵C(0,-3),
∴OC=3,
∴S△ABC=AB·OC=×4×3=6.
8分
18.解:如图,过点C作CE⊥AB于点E.设AE=x.
在Rt△ACE中,CE=≈1.11x.
2分
在Rt△AFE中,FE=≈0.56x.
4分
由题意,得CF=CE-FE≈1.11x-0.56x=12,
解得x≈21.82.
6分
故AB=AE+BE≈21.82+1.5≈23(米).
答:白塔的高度AB约为23米.
8分
19.解:(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB.
2分
∵AC2=AB·AD,
∴=,
∴△ADC∽△ACB.
4分
(2)∵△ADC∽△ACB,
∴∠ACB=∠ADC=90°.
6分
∵E为AB的中点,
∴CE=AE=AB=,
∴∠EAC=∠ECA.
∵∠DAC=∠EAC,
∴∠DAC=∠ECA,
∴CE∥AD.
8分
∴==,
∴=.
10分
20.解:(1)把点A(2,1)代入y2=,得k2=2,
∴y2=.
把点A(2,1),点C(0,3)代入y1=k1x+b,得解得
∴y1=-x+3.
3分
令y1=y2,即-x+3=,解得x1=2,x2=1,经检验x1=2,x2=1均为原方程的解.
由题意可知x1=2应舍去,
∴点B的坐标为(1,2).
6分
(2)观察图象可得当0
当x=1或x=2时,y1=y2.
10分
21.解:(1)由题意,得抛物线的顶点坐标为(3,9),且经过点(5,10).
设y2与x之间的函数表达式为y2=a(x-3)2+9.
2分
将(5,10)代入y2=a(x-3)2+9,得a(5-3)2+9=10,解得a=,
∴y2与x之间的函数表达式为y2=(x-3)2+9=x2-x+.
6分
(2)由题意,得
w=y1-y2=2x+6-(x2-x+)
=-x2+x-
=-(x-7)2+7.
∴当x=7时,w取得最大值7.
∴7月份销售每千克猪肉所获的利润最大,最大利润是7元.
12分
22.解:(1)证明:∵DE⊥AB,AG⊥BC,
∴∠BED=∠BGA=90°.
∵∠B=∠B,
∴△DBE∽△ABG.
4分
(2)∵BC=10,AB=AC=13,∴BG=5,
∴AG=12.
设BD=x,则CD=10-x.
∵△DBE∽△ABG,∴=,
∴ED=x.
∵DF∥AB,
∴∠EDF=∠BED=90°,=,
∴DF=1.3(10-x),
∴△DEF的面积=×x×1.3(10-x)
8分
=0.6x(10-x)
=-0.6(x-5)2+15.
∴当△DEF的面积最大时,x=5,即BD的长为5.
12分
23.解:(1)如图①,作FH⊥BC于点H,MQ⊥CD于点Q.
∵四边形ABCD是正方形,FH=AB,MQ=BC,
∴FH=MQ.
∵EF⊥MN,
∴∠EPN=90°.
∵∠ECN=90°,
∴∠MNQ+∠CEP=180°.
∵∠FEH+∠CEP=180°,
∴∠FEH=∠MNQ.
又∵∠EHF=∠NQM=90°,
∴△FHE≌△MQN,
4分
∴MN=EF,
∴k=MN∶EF=1.
6分
(2)连接FN,ME.
∵k=3,MP=EF=3PE,
∴===3,∴==2.
又∠FPN=∠EPM,∴△PNF∽△PME,
∴==2,∠FNP=∠EMP,
∴ME∥NF.
9分
设PE=2m,则PF=4m,MP=6m,PN=12m.
①如图②,当点N与点D重合时,点M恰好与点B重合.作FH⊥BD于点H.
∵∠MPE=∠FPH=60°,PF=4m,
∴PH=2m,FH=2m,
∴DH=PN-PH=10m,
∴==tan∠ADB==.
11分
②如图③,当点N与点C重合时,作EH⊥MN于点H,则易得PH=m,HE=m,
∴HC=PH+PN=13m.
∴tan∠HCE===.
∵ME∥NF,AD∥BC,
∴∠MEB=∠FNB=∠NFD.
∵∠B=∠D,
∴△MEB∽△NFD.
∴==2,
∴===.综上所述,a∶b的值为或.
14分
