第06讲 12.2 全等三角形的性质与判断讲义2021-2022学年八年级数学人教版上册(无答案)
文档属性
| 名称 | 第06讲 12.2 全等三角形的性质与判断讲义2021-2022学年八年级数学人教版上册(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 57.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 09:38:30 | ||
图片预览

文档简介
第十二章 全等三角形
第6讲 全等三角形的性质与判断
知识导航
全等三角形性质与判断的应用;
全等的简单构造.
全等三角形常见基本构图类型
板块一 全等三角形的性质与判断的应用
方法技巧
依据三角形全等的条件证明三角形全等从而得到边等角等
题型一 一次全等
这类问题题目条件和结论一般都指向同一对三角形,属于全等条件比较直接的类型,一次全等便可解决问题.
如图,B,E,C,F四点在同一直线上,BE=CF,AB=DE ,且AB∥DE判断线段AC,DF的关系并证明.
如图,AB=AC,BE⊥AC,CD⊥AB于D,求证BD=CE.
题型二 二次全等
这类问题题目条件和待求问题一般都不是指向于同一对三角形,即条件较容易得出的全等三角形,并不能直接得出要证明的边角相等,但是可以得出待求边角所在的三角形全等所缺少的条件,于是两次全等便可解决问题.
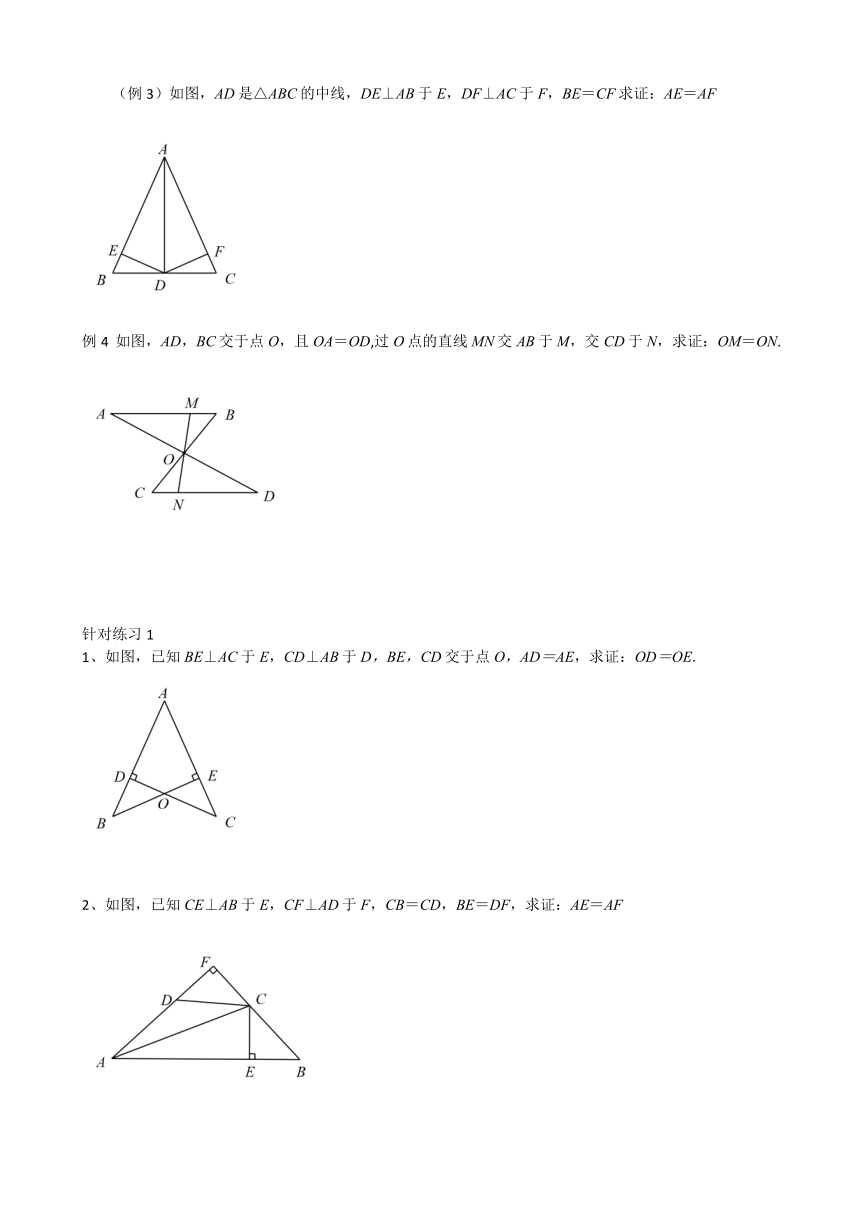
(例3)如图,AD是△ABC的中线,DE⊥AB于E,DF⊥AC于F,BE=CF求证:AE=AF
例4 如图,AD,BC交于点O,且OA=OD,过O点的直线MN交AB于M,交CD于N,求证:OM=ON.
针对练习1
1、如图,已知BE⊥AC于E,CD⊥AB于D,BE,CD交于点O,AD=AE,求证:OD=OE.
2、如图,已知CE⊥AB于E,CF⊥AD于F,CB=CD,BE=DF,求证:AE=AF
板块二 全等的简单构造
方法技巧
题目条件或结论所指向的三角形不存在,或部分残缺,如果只需要连接某些线段或作适当添补便可得到全等三角形并且可以有效解决问题,这时便可运用辅助线构造全等.
题型一 简单连线构造
(例5)如图四边形ABCD中,AB=CD,AD=BC,求证:∠A=∠C
(例6)如图,AB,CD交于点O,AB=CD,AC=BD,求证:∠A=∠D
题型二 已知一角和角的一边相等(SA)截取边等构造(SAS)全等
(例7)如图,∠BAC=∠BDC=90°,AB=AC,求证:∠ADB=45°
题型三 已知一角和角的一边相等(SA)作垂直,构造(AAS或ASA)全等
例8 如图,∠BAC=∠BDC=90°,AB=AC,求:∠ADB的度数.
题型四 作平行构造全等
(例9)如图,在△ABC中,∠ABC=∠ACB,点D为AB上一点,点E为AC延长线上一点,DE交BC于M,MD=ME,求证:BD=CE
题型五 补形构造全等
(例10)如图,△ABC中,∠ABC=90°,AB=BC,AE平分∠BAC,交BC于点E,CD⊥AE于D,求证:AE=2CD
针对练习2
1.如图,在四边形ABCD中,∠B=∠D=90°,BC=CD,求证:AB=AD
2.如图,五边形ABCDE中,点F为CD上一点,连接AF.
(1)若AB=AE,∠B=∠E,BC=ED,AF⊥CD,求证:F为CD中点;
(2)若AB=AE,∠B=∠E,AF平分∠BAE,AF⊥CD,求证:F为CD中点.
第6讲 全等三角形的性质与判断
知识导航
全等三角形性质与判断的应用;
全等的简单构造.
全等三角形常见基本构图类型
板块一 全等三角形的性质与判断的应用
方法技巧
依据三角形全等的条件证明三角形全等从而得到边等角等
题型一 一次全等
这类问题题目条件和结论一般都指向同一对三角形,属于全等条件比较直接的类型,一次全等便可解决问题.
如图,B,E,C,F四点在同一直线上,BE=CF,AB=DE ,且AB∥DE判断线段AC,DF的关系并证明.
如图,AB=AC,BE⊥AC,CD⊥AB于D,求证BD=CE.
题型二 二次全等
这类问题题目条件和待求问题一般都不是指向于同一对三角形,即条件较容易得出的全等三角形,并不能直接得出要证明的边角相等,但是可以得出待求边角所在的三角形全等所缺少的条件,于是两次全等便可解决问题.
(例3)如图,AD是△ABC的中线,DE⊥AB于E,DF⊥AC于F,BE=CF求证:AE=AF
例4 如图,AD,BC交于点O,且OA=OD,过O点的直线MN交AB于M,交CD于N,求证:OM=ON.
针对练习1
1、如图,已知BE⊥AC于E,CD⊥AB于D,BE,CD交于点O,AD=AE,求证:OD=OE.
2、如图,已知CE⊥AB于E,CF⊥AD于F,CB=CD,BE=DF,求证:AE=AF
板块二 全等的简单构造
方法技巧
题目条件或结论所指向的三角形不存在,或部分残缺,如果只需要连接某些线段或作适当添补便可得到全等三角形并且可以有效解决问题,这时便可运用辅助线构造全等.
题型一 简单连线构造
(例5)如图四边形ABCD中,AB=CD,AD=BC,求证:∠A=∠C
(例6)如图,AB,CD交于点O,AB=CD,AC=BD,求证:∠A=∠D
题型二 已知一角和角的一边相等(SA)截取边等构造(SAS)全等
(例7)如图,∠BAC=∠BDC=90°,AB=AC,求证:∠ADB=45°
题型三 已知一角和角的一边相等(SA)作垂直,构造(AAS或ASA)全等
例8 如图,∠BAC=∠BDC=90°,AB=AC,求:∠ADB的度数.
题型四 作平行构造全等
(例9)如图,在△ABC中,∠ABC=∠ACB,点D为AB上一点,点E为AC延长线上一点,DE交BC于M,MD=ME,求证:BD=CE
题型五 补形构造全等
(例10)如图,△ABC中,∠ABC=90°,AB=BC,AE平分∠BAC,交BC于点E,CD⊥AE于D,求证:AE=2CD
针对练习2
1.如图,在四边形ABCD中,∠B=∠D=90°,BC=CD,求证:AB=AD
2.如图,五边形ABCDE中,点F为CD上一点,连接AF.
(1)若AB=AE,∠B=∠E,BC=ED,AF⊥CD,求证:F为CD中点;
(2)若AB=AE,∠B=∠E,AF平分∠BAE,AF⊥CD,求证:F为CD中点.
