第23章 解直角三角形单元练习阶段测试 2021-2022学年沪科版九年级数学上册(Word版含答案)
文档属性
| 名称 | 第23章 解直角三角形单元练习阶段测试 2021-2022学年沪科版九年级数学上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 194.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 00:00:00 | ||
图片预览



文档简介
阶段测试(三)
[范围:第23章 时间:120分钟 分值:150分]
一、选择题(本大题共10小题,每小题4分,满分40分)
1.2cos60°的值为
( )
A.1
B.
C.
D.
2.把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定
3.在Rt△ABC中,若∠C=90°,BC=6,AC=8,则tanA的值为
( )
A.
B.
C.
D.
4.在Rt△ABC中,∠C=90°,如果cosA=,那么tanB的值为
( )
A.
B.
C.
D.
5.在△ABC中,a,b,c分别为∠A,∠B,∠C的对边,如果三边a,b,c的长分别为1,2,,那么cosA的值为
( )
A.
B.
C.
D.
6.如图1,河堤横断面迎水坡AB的坡比是1∶,堤高BC=4米,则迎水坡的宽度AC的长为
( )
图1
A.4米
B.
米
C.8米
D.4米
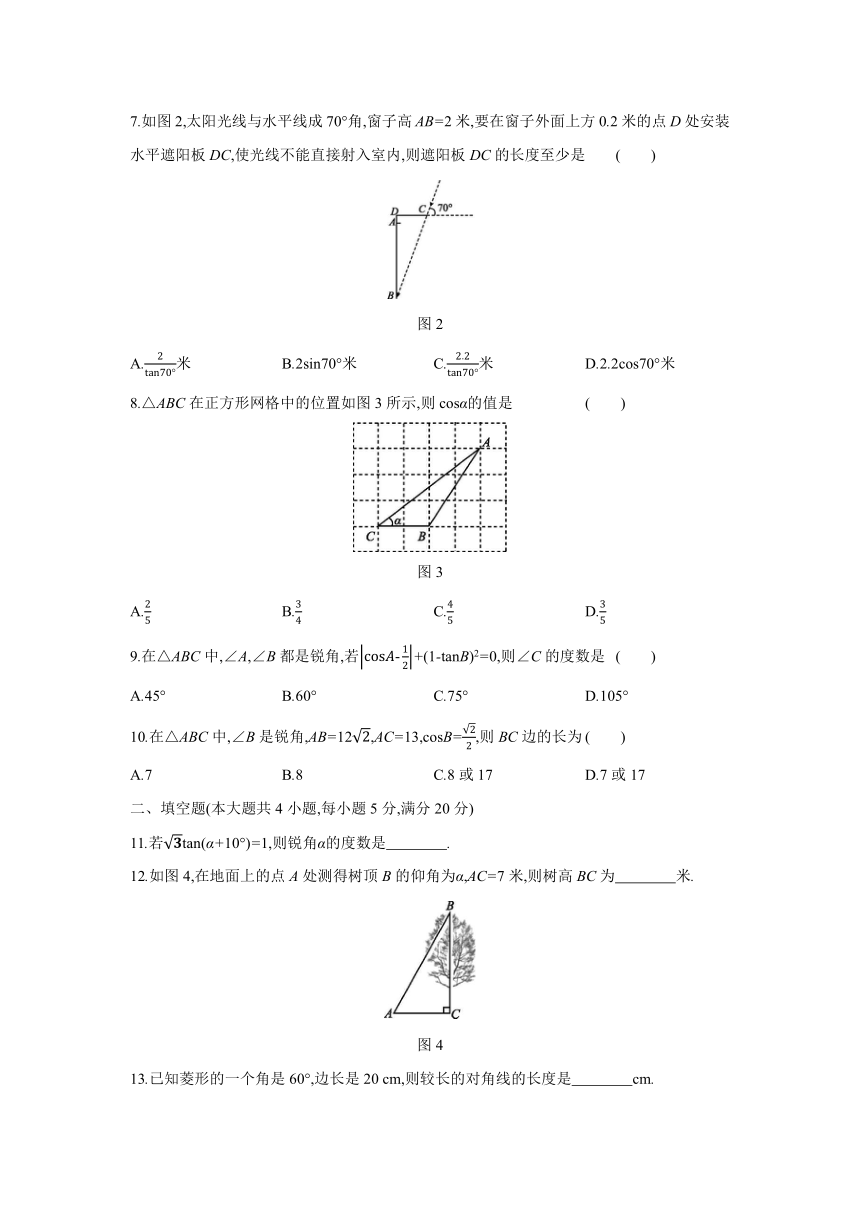
7.如图2,太阳光线与水平线成70°角,窗子高AB=2米,要在窗子外面上方0.2米的点D处安装水平遮阳板DC,使光线不能直接射入室内,则遮阳板DC的长度至少是
( )
图2
A.米
B.2sin70°米
C.米
D.2.2cos70°米
8.△ABC在正方形网格中的位置如图3所示,则cosα的值是
( )
图3
A.
B.
C.
D.
9.在△ABC中,∠A,∠B都是锐角,若+(1-tanB)2=0,则∠C的度数是
( )
A.45°
B.60°
C.75°
D.105°
10.在△ABC中,∠B是锐角,AB=12,AC=13,cosB=,则BC边的长为
( )
A.7
B.8
C.8或17
D.7或17
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若tan(α+10°)=1,则锐角α的度数是 .?
12.如图4,在地面上的点A处测得树顶B的仰角为α,AC=7米,则树高BC为 米.?
图4
13.已知菱形的一个角是60°,边长是20
cm,则较长的对角线的长度是 cm.?
14.在平面直角坐标系xOy中,已知一次函数y=kx+b的图象经过点P(1,1),与x轴交于点A,与y轴交于点B,且tan∠ABO=3,那么点A的坐标是 .?
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(1)sin60°-cos45°+;
(2)-22-+|1-4sin60°|+.
16.如图5,在等腰三角形ABC中,AB=AC=5,BC=6,求锐角B的三角函数值.
图5
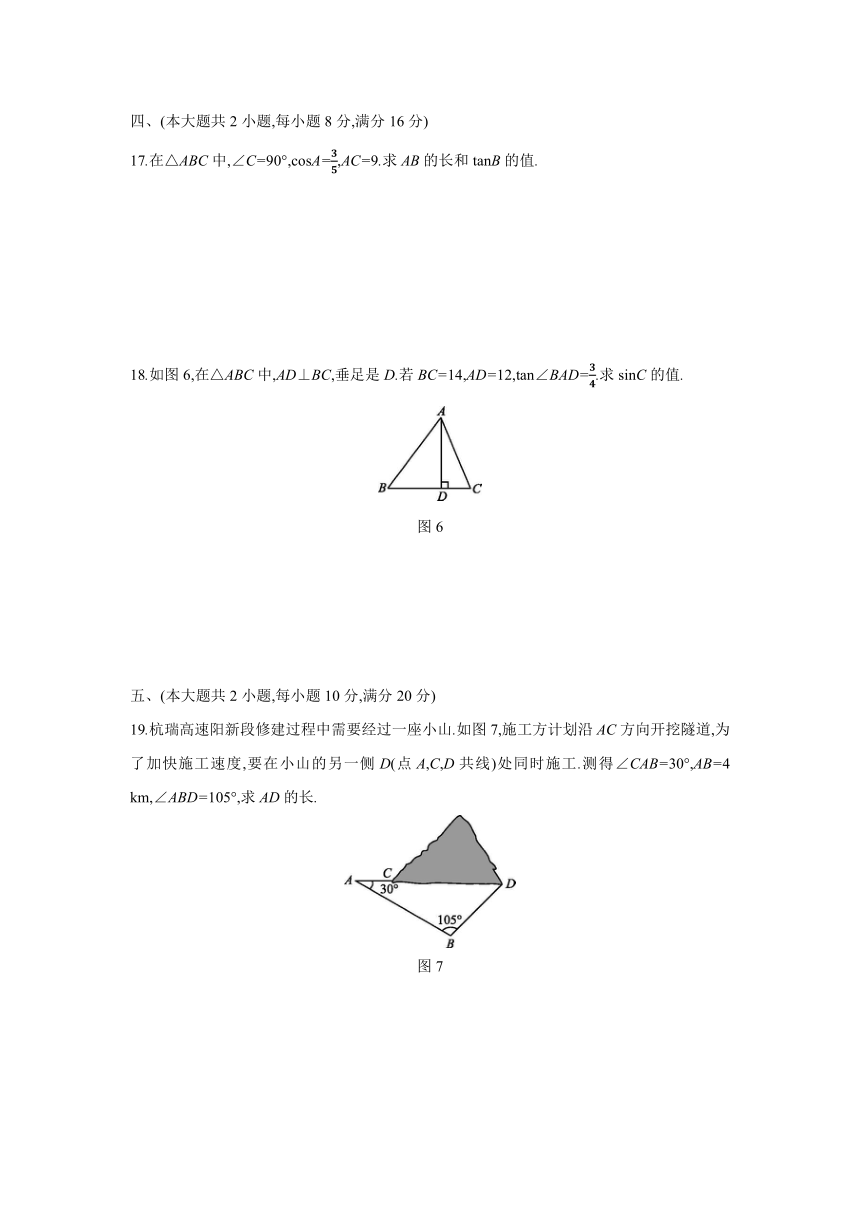
四、(本大题共2小题,每小题8分,满分16分)
17.在△ABC中,∠C=90°,cosA=,AC=9.求AB的长和tanB的值.
18.如图6,在△ABC中,AD⊥BC,垂足是D.若BC=14,AD=12,tan∠BAD=.求sinC的值.
图6
五、(本大题共2小题,每小题10分,满分20分)
19.杭瑞高速阳新段修建过程中需要经过一座小山.如图7,施工方计划沿AC方向开挖隧道,为了加快施工速度,要在小山的另一侧D(点A,C,D共线)处同时施工.测得∠CAB=30°,AB=4
km,∠ABD=105°,求AD的长.
图7
20.某校兴趣小组坐游轮拍摄海河两岸的美景.如图8,游轮出发点A与望海楼B的距离为300
m,在A处测得望海楼B位于A的北偏东30°方向,游轮沿正北方向行驶一段时间后到达C处,在C处测得望海楼B位于点C的北偏东60°方向.求此时游轮与望海楼之间的距离BC(≈1.732.结果保留整数).
图8
六、(本题满分12分)
21.如图9,在大楼AB的正前方有一斜坡CD,CD=13米,坡度为5∶12,高为DE,在斜坡下的点C处测得楼顶B的仰角为58°,在斜坡上的点D处测得楼顶B的仰角为31°,其中点A,C,E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度
(结果保留一位小数.参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,sin31°≈0.52,cos31°≈0.86,
tan31°≈0.60).
图9
七、(本题满分12分)
22.我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can).如图10①,在△ABC中,AB=AC,底角∠B的邻对记作canB,这时canB==.容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解下列问题:
(1)can30°= ;?
(2)如图②,已知在△ABC中,AB=AC,canB=,S△ABC=24,求△ABC的周长.
图10
八、(本题满分14分)
23.九年级(1)班同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.
(1)如图11①,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等.如果测量得到∠CDB=38°,求护墙与地面的倾斜角α的度数;
(2)如图②(示意图),第二小组用皮尺量得EF的长为16
m(E为护墙上的端点),EF的中点M离地面FB的高度为1.9
m,请求出点E离地面FB的高度;
(3)如图③,第三小组利用第二小组的结果,来测量护墙上旗杆的高度.在点P处测得旗杆顶端A的仰角为45°,向前走4
m到达点Q,测得点A的仰角为60°.求旗杆AE的高度.(精确到0.1
m.参考数据:≈1.732,≈1.414)
图11
教师详解详析
1.A 2.A 3.B 4.D
5.B 6.A 7.C 8.C
9.C 10.D
11.20°
12.7tanα
13.20
14.(4,0)或(-2,0)
15.解:(1)原式=×-×+2
2分
=-1+2
=.
4分
(2)原式=-4-2++1
6分
=-4-2+2-1+1
=-4.
8分
16.解:如图,过点A作AD⊥BC于点D.
∵AB=AC,∴BD=BC=3.
2分
在Rt△ABD中,AD==4.
4分
∴sinB==,cosB==,tanB==.
8分
17.解:∵在△ABC中,∠C=90°,cosA==,AC=9,∴AB===15.
4分
根据勾股定理,得BC==12.
∴tanB===.
8分
18.解:∵在Rt△ABD中,tan∠BAD==,
∴BD=AD·tan∠BAD=12×=9.
∴CD=BC-BD=14-9=5.
4分
在Rt△ACD中,AC===13.
6分
∴sinC==.
8分
19.解:过点B作BE⊥AD于点E,如图所示.
在Rt△ABE中,AB=4
km,∠CAB=30°,∠AEB=90°,
∴BE=AB=2(km),AE=AB·cos30°=4×=2(km),∠ABE=90°-30°=60°,
4分
∴∠DBE=∠ABD-∠ABE=105°-60°=45°.
在Rt△BDE中,∠BED=90°,∠DBE=45°,
∴DE=BE·tan∠DBE=2(km),
8分
∴AD=AE+DE=(2+2)km.
10分
20.解:如图,过点B作BD⊥AC,交AC的延长线于点D.
在Rt△ADB中,∠BAD=30°,AB=300,
∴BD=AB=×300=150.
5分
在Rt△CDB中,∵sin∠DCB=,
∴BC===≈173(m).
答:此时游轮与望海楼之间的距离BC约为173
m.
10分
21.解:(1)∵在大楼AB的正前方有一斜坡CD,CD=13米,坡度为5∶12,
∴=.
2分
设DE=5x米,则EC=12x米,
∴(5x)2+(12x)2=132,
解得x=1(负值已舍去),
∴5x=5,12x=12,
即DE=5米,EC=12米,
故斜坡CD的高度DE是5米.
6分
(2)过点D作DF⊥AB于点F,则AF=DE=5.
∴BF=AB-5.在Rt△BDF中,DF=,
在Rt△ABC中,AC=,
∴AE=EC+AC=12+.
∵DF=AE,
∴=12+,
解得AB≈19.5.
即大楼AB的高度约为19.5米.
12分
22.解:(1)如图①,过点A作AD⊥BC于点D.
∵∠B=30°,∴cosB==.
∴BD=AB.
2分
∵△ABC是等腰三角形,
∴BC=2BD=AB.
∴can30°==.
故答案为.
6分
(2)如图②,过点A作AE⊥BC于点E.
∵canB=,
∴设BC=8x,AB=5x,则BE=4x.
∴AE==3x.
8分
∵S△ABC=24,
∴BC·AE=12x2=24.
解得x=(负值已舍去).
∴AB=AC=5,BC=8.
10分
∴△ABC的周长=AB+AC+BC=5+5+8=18.
12分
23.解:(1)∵DB=CB,∴∠CDB=∠BCD.
∵∠CDB=38°,
∴α=∠CDB+∠BCD=2∠CDB=76°.
即护墙与地面的倾斜角α的度数为76°.
4分
(2)如图①,过点E作EG⊥FB于点G,过点M作MN⊥FB于点N.
∵EG⊥FB,MN⊥FB,
∴EG∥MN.
6分
又∵M是线段EF的中点,根据平行线分线段成比例可得N是线段FG的中点,
∴MN是△EFG的中位线.
∴EG=2MN=2×1.9=3.8(m).
即点E离地面FB的高度为3.8
m.
8分
(3)如图②,延长AE交PB的延长线于点H.
在Rt△AQH中,由tan∠AQH=,得QH==.
同理,PH==AH.
10分
∵PQ=4
m,
∴PH-QH=AH-AH=4,
解得AH≈9.46(m).
∴AE=AH-EH≈9.46-3.8≈5.7(m).
答:旗杆AE的高度约为5.7
m.
14分
[范围:第23章 时间:120分钟 分值:150分]
一、选择题(本大题共10小题,每小题4分,满分40分)
1.2cos60°的值为
( )
A.1
B.
C.
D.
2.把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦值( )
A.不变
B.缩小为原来的
C.扩大为原来的3倍
D.不能确定
3.在Rt△ABC中,若∠C=90°,BC=6,AC=8,则tanA的值为
( )
A.
B.
C.
D.
4.在Rt△ABC中,∠C=90°,如果cosA=,那么tanB的值为
( )
A.
B.
C.
D.
5.在△ABC中,a,b,c分别为∠A,∠B,∠C的对边,如果三边a,b,c的长分别为1,2,,那么cosA的值为
( )
A.
B.
C.
D.
6.如图1,河堤横断面迎水坡AB的坡比是1∶,堤高BC=4米,则迎水坡的宽度AC的长为
( )
图1
A.4米
B.
米
C.8米
D.4米
7.如图2,太阳光线与水平线成70°角,窗子高AB=2米,要在窗子外面上方0.2米的点D处安装水平遮阳板DC,使光线不能直接射入室内,则遮阳板DC的长度至少是
( )
图2
A.米
B.2sin70°米
C.米
D.2.2cos70°米
8.△ABC在正方形网格中的位置如图3所示,则cosα的值是
( )
图3
A.
B.
C.
D.
9.在△ABC中,∠A,∠B都是锐角,若+(1-tanB)2=0,则∠C的度数是
( )
A.45°
B.60°
C.75°
D.105°
10.在△ABC中,∠B是锐角,AB=12,AC=13,cosB=,则BC边的长为
( )
A.7
B.8
C.8或17
D.7或17
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若tan(α+10°)=1,则锐角α的度数是 .?
12.如图4,在地面上的点A处测得树顶B的仰角为α,AC=7米,则树高BC为 米.?
图4
13.已知菱形的一个角是60°,边长是20
cm,则较长的对角线的长度是 cm.?
14.在平面直角坐标系xOy中,已知一次函数y=kx+b的图象经过点P(1,1),与x轴交于点A,与y轴交于点B,且tan∠ABO=3,那么点A的坐标是 .?
三、(本大题共2小题,每小题8分,满分16分)
15.计算:(1)sin60°-cos45°+;
(2)-22-+|1-4sin60°|+.
16.如图5,在等腰三角形ABC中,AB=AC=5,BC=6,求锐角B的三角函数值.
图5
四、(本大题共2小题,每小题8分,满分16分)
17.在△ABC中,∠C=90°,cosA=,AC=9.求AB的长和tanB的值.
18.如图6,在△ABC中,AD⊥BC,垂足是D.若BC=14,AD=12,tan∠BAD=.求sinC的值.
图6
五、(本大题共2小题,每小题10分,满分20分)
19.杭瑞高速阳新段修建过程中需要经过一座小山.如图7,施工方计划沿AC方向开挖隧道,为了加快施工速度,要在小山的另一侧D(点A,C,D共线)处同时施工.测得∠CAB=30°,AB=4
km,∠ABD=105°,求AD的长.
图7
20.某校兴趣小组坐游轮拍摄海河两岸的美景.如图8,游轮出发点A与望海楼B的距离为300
m,在A处测得望海楼B位于A的北偏东30°方向,游轮沿正北方向行驶一段时间后到达C处,在C处测得望海楼B位于点C的北偏东60°方向.求此时游轮与望海楼之间的距离BC(≈1.732.结果保留整数).
图8
六、(本题满分12分)
21.如图9,在大楼AB的正前方有一斜坡CD,CD=13米,坡度为5∶12,高为DE,在斜坡下的点C处测得楼顶B的仰角为58°,在斜坡上的点D处测得楼顶B的仰角为31°,其中点A,C,E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度
(结果保留一位小数.参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,sin31°≈0.52,cos31°≈0.86,
tan31°≈0.60).
图9
七、(本题满分12分)
22.我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can).如图10①,在△ABC中,AB=AC,底角∠B的邻对记作canB,这时canB==.容易知道一个角的大小与这个角的邻对值是一一对应的,根据上述角的邻对的定义,解下列问题:
(1)can30°= ;?
(2)如图②,已知在△ABC中,AB=AC,canB=,S△ABC=24,求△ABC的周长.
图10
八、(本题满分14分)
23.九年级(1)班同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.
(1)如图11①,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等.如果测量得到∠CDB=38°,求护墙与地面的倾斜角α的度数;
(2)如图②(示意图),第二小组用皮尺量得EF的长为16
m(E为护墙上的端点),EF的中点M离地面FB的高度为1.9
m,请求出点E离地面FB的高度;
(3)如图③,第三小组利用第二小组的结果,来测量护墙上旗杆的高度.在点P处测得旗杆顶端A的仰角为45°,向前走4
m到达点Q,测得点A的仰角为60°.求旗杆AE的高度.(精确到0.1
m.参考数据:≈1.732,≈1.414)
图11
教师详解详析
1.A 2.A 3.B 4.D
5.B 6.A 7.C 8.C
9.C 10.D
11.20°
12.7tanα
13.20
14.(4,0)或(-2,0)
15.解:(1)原式=×-×+2
2分
=-1+2
=.
4分
(2)原式=-4-2++1
6分
=-4-2+2-1+1
=-4.
8分
16.解:如图,过点A作AD⊥BC于点D.
∵AB=AC,∴BD=BC=3.
2分
在Rt△ABD中,AD==4.
4分
∴sinB==,cosB==,tanB==.
8分
17.解:∵在△ABC中,∠C=90°,cosA==,AC=9,∴AB===15.
4分
根据勾股定理,得BC==12.
∴tanB===.
8分
18.解:∵在Rt△ABD中,tan∠BAD==,
∴BD=AD·tan∠BAD=12×=9.
∴CD=BC-BD=14-9=5.
4分
在Rt△ACD中,AC===13.
6分
∴sinC==.
8分
19.解:过点B作BE⊥AD于点E,如图所示.
在Rt△ABE中,AB=4
km,∠CAB=30°,∠AEB=90°,
∴BE=AB=2(km),AE=AB·cos30°=4×=2(km),∠ABE=90°-30°=60°,
4分
∴∠DBE=∠ABD-∠ABE=105°-60°=45°.
在Rt△BDE中,∠BED=90°,∠DBE=45°,
∴DE=BE·tan∠DBE=2(km),
8分
∴AD=AE+DE=(2+2)km.
10分
20.解:如图,过点B作BD⊥AC,交AC的延长线于点D.
在Rt△ADB中,∠BAD=30°,AB=300,
∴BD=AB=×300=150.
5分
在Rt△CDB中,∵sin∠DCB=,
∴BC===≈173(m).
答:此时游轮与望海楼之间的距离BC约为173
m.
10分
21.解:(1)∵在大楼AB的正前方有一斜坡CD,CD=13米,坡度为5∶12,
∴=.
2分
设DE=5x米,则EC=12x米,
∴(5x)2+(12x)2=132,
解得x=1(负值已舍去),
∴5x=5,12x=12,
即DE=5米,EC=12米,
故斜坡CD的高度DE是5米.
6分
(2)过点D作DF⊥AB于点F,则AF=DE=5.
∴BF=AB-5.在Rt△BDF中,DF=,
在Rt△ABC中,AC=,
∴AE=EC+AC=12+.
∵DF=AE,
∴=12+,
解得AB≈19.5.
即大楼AB的高度约为19.5米.
12分
22.解:(1)如图①,过点A作AD⊥BC于点D.
∵∠B=30°,∴cosB==.
∴BD=AB.
2分
∵△ABC是等腰三角形,
∴BC=2BD=AB.
∴can30°==.
故答案为.
6分
(2)如图②,过点A作AE⊥BC于点E.
∵canB=,
∴设BC=8x,AB=5x,则BE=4x.
∴AE==3x.
8分
∵S△ABC=24,
∴BC·AE=12x2=24.
解得x=(负值已舍去).
∴AB=AC=5,BC=8.
10分
∴△ABC的周长=AB+AC+BC=5+5+8=18.
12分
23.解:(1)∵DB=CB,∴∠CDB=∠BCD.
∵∠CDB=38°,
∴α=∠CDB+∠BCD=2∠CDB=76°.
即护墙与地面的倾斜角α的度数为76°.
4分
(2)如图①,过点E作EG⊥FB于点G,过点M作MN⊥FB于点N.
∵EG⊥FB,MN⊥FB,
∴EG∥MN.
6分
又∵M是线段EF的中点,根据平行线分线段成比例可得N是线段FG的中点,
∴MN是△EFG的中位线.
∴EG=2MN=2×1.9=3.8(m).
即点E离地面FB的高度为3.8
m.
8分
(3)如图②,延长AE交PB的延长线于点H.
在Rt△AQH中,由tan∠AQH=,得QH==.
同理,PH==AH.
10分
∵PQ=4
m,
∴PH-QH=AH-AH=4,
解得AH≈9.46(m).
∴AE=AH-EH≈9.46-3.8≈5.7(m).
答:旗杆AE的高度约为5.7
m.
14分
