9.2多边形的内角和(第2课时)课件
文档属性
| 名称 | 9.2多边形的内角和(第2课时)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 96.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-19 00:00:00 | ||
图片预览




文档简介
(共11张PPT)
复习
n边形的内角和为_________________.
(n-2) 180 °
它有什么作用呢
1.知道多边形的边数,可以求出多边形的度数.
2.知道多边形的度数,可以求出多边形的边数.
例1.求八边形的内角和的度数.
解 (n-2)×180°
=(8-2)×180°
=1 080°
分析: n边形的内角和公式为(n-2) 180 ° ,
现在知道这个多边形的边数是,
代入这个公式既可求出.
老师,可以用计算器吗
例2.如果一个正多边形的一个内角等于120°,则这个多边形的边数是_____
解: 120°n=(n-2)×180°
120°n=n×180°-360 °
60°n =360 °
n =6
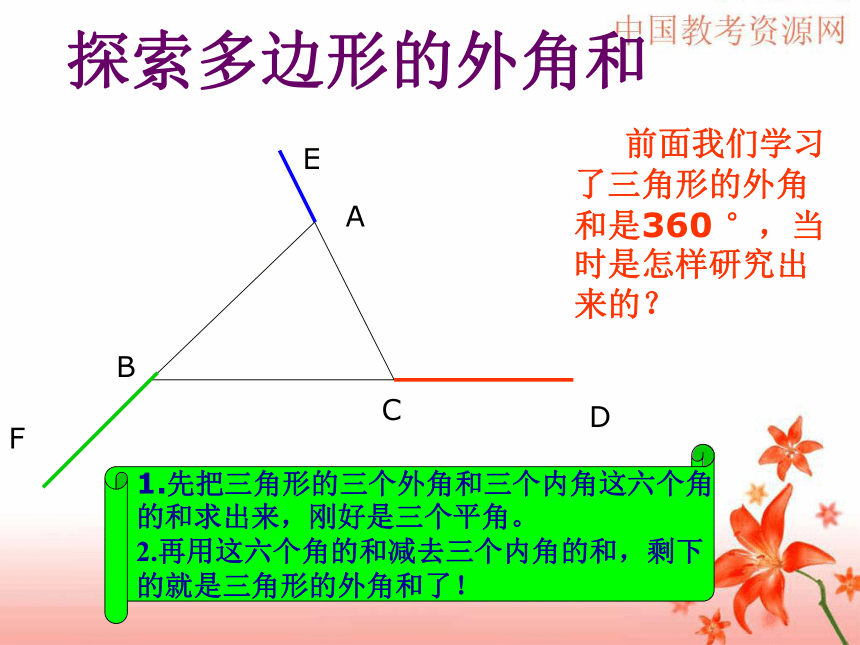
前面我们学习了三角形的外角和是360 °,当时是怎样研究出来的?
A
B
C
D
E
F
1.先把三角形的三个外角和三个内角这六个角
的和求出来,刚好是三个平角。
2.再用这六个角的和减去三个内角的和,剩下
的就是三角形的外角和了!
探索多边形的外角和
那么你能研究出四边形的外角和吗?
整体思路:1.先求4个外角+4个内角的和;
2.再减去4个内角的和
容易看出,4个外角+4个内角=4个平角
而4个内角的和是360 ° ,
那么四边形的外角和就是4X 180°-360°= 360°
那么出五边形,六边形,n边形的外角和吗?
五边形的外角和就是5X 180°-540°= 360 °
六边形的外角和就是6X 180°-720°= 360°
。。。。。。
n边形的外角和就是nX 180°- (n-2)X 180°
= (n-n+2)X 180° = 360 °
任意多边形的外角和都为3
6
0 °
例3.正五边形的每一个外角等于___.每一个内角等于_____,
72°
144°
例4.如果一个正多边形的一个内角等于120°,则这个多边形的边数是_____
6
例5.如果一个正多边形的一个内角等于150°,则这个多边形的边数是( )
A.12 B.9 C. 8 D.7
A
例6.如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____
12
例7.一个正多边形的一个内角和是外角和的2倍,则这个多边形为( )
A.三角形 B.四边形 C.五边形 D. 六边形
例8.一个正多边形的一个内角和与外角和的比是7:2,则这个多边形的边数为 。
今天你学到了什么知识?你能用自己的话说说吗?
复习
n边形的内角和为_________________.
(n-2) 180 °
它有什么作用呢
1.知道多边形的边数,可以求出多边形的度数.
2.知道多边形的度数,可以求出多边形的边数.
例1.求八边形的内角和的度数.
解 (n-2)×180°
=(8-2)×180°
=1 080°
分析: n边形的内角和公式为(n-2) 180 ° ,
现在知道这个多边形的边数是,
代入这个公式既可求出.
老师,可以用计算器吗
例2.如果一个正多边形的一个内角等于120°,则这个多边形的边数是_____
解: 120°n=(n-2)×180°
120°n=n×180°-360 °
60°n =360 °
n =6
前面我们学习了三角形的外角和是360 °,当时是怎样研究出来的?
A
B
C
D
E
F
1.先把三角形的三个外角和三个内角这六个角
的和求出来,刚好是三个平角。
2.再用这六个角的和减去三个内角的和,剩下
的就是三角形的外角和了!
探索多边形的外角和
那么你能研究出四边形的外角和吗?
整体思路:1.先求4个外角+4个内角的和;
2.再减去4个内角的和
容易看出,4个外角+4个内角=4个平角
而4个内角的和是360 ° ,
那么四边形的外角和就是4X 180°-360°= 360°
那么出五边形,六边形,n边形的外角和吗?
五边形的外角和就是5X 180°-540°= 360 °
六边形的外角和就是6X 180°-720°= 360°
。。。。。。
n边形的外角和就是nX 180°- (n-2)X 180°
= (n-n+2)X 180° = 360 °
任意多边形的外角和都为3
6
0 °
例3.正五边形的每一个外角等于___.每一个内角等于_____,
72°
144°
例4.如果一个正多边形的一个内角等于120°,则这个多边形的边数是_____
6
例5.如果一个正多边形的一个内角等于150°,则这个多边形的边数是( )
A.12 B.9 C. 8 D.7
A
例6.如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____
12
例7.一个正多边形的一个内角和是外角和的2倍,则这个多边形为( )
A.三角形 B.四边形 C.五边形 D. 六边形
例8.一个正多边形的一个内角和与外角和的比是7:2,则这个多边形的边数为 。
今天你学到了什么知识?你能用自己的话说说吗?
