人教A版(2019)选择性必修第一册第一章 空间向量与立体几何1.1 空间向量及其运算(线性运算、数量积运算)(共59张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册第一章 空间向量与立体几何1.1 空间向量及其运算(线性运算、数量积运算)(共59张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 00:00:00 | ||
图片预览








文档简介
(共59张PPT)
第1课时 空间向量的线性运算
重难点:1.会用图形说明空间向量加法、减法、数
乘向量及它们的运算律.
2.能运用空间向量的运算意义及运算律解
决简单的立体几何问题.
与平面向量一样:
一、空间向量的概念
(1)向量:在空间中,具_________和______的量.
(2)向量a的长度或模:表示向量a的有向线段的长度,记作|a|.
(3)零向量:长度为______的向量。(手写记作
)
单位向量:长度为_______的向量。
(4)相等向量:在空间,方向相同且模相等的向量。
(5)相反向量:长度_______方向________的向量。
(6)共线向量或平行向量:如果表示若干空间向量的有向线段所在的直线互相平行或重合。
规定:零向量与任意向量共线.
大小
方向
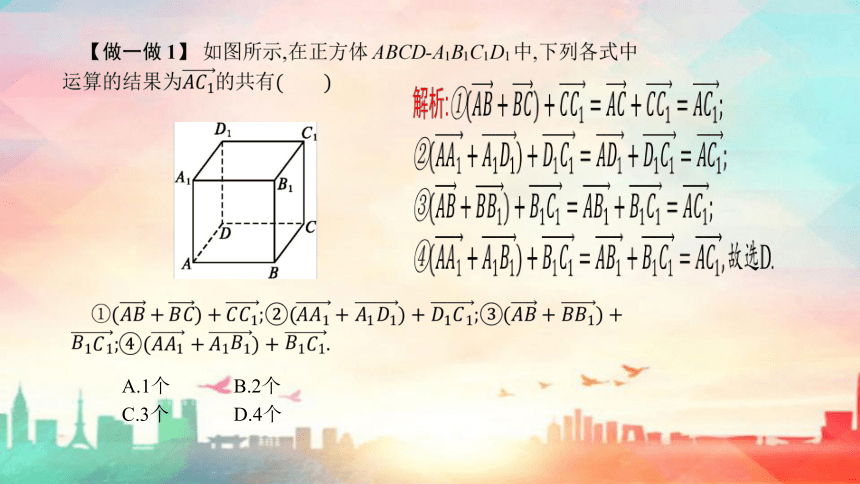
做一做1、正方体ABCD
-
A'B'C'D'中与向量相等的向量有_____
1
相等
相反
0
3
已知空间向量
,以任意点O为起点
,作向量
,我们就可以把他们平移到同一平面
,这样任意的两个空间向量的运算就可以转化为平面向量运算。由此,我们把平面向量的运算推广到空间,定义空间向量的加减法以及数乘运算:
A.1个
B.2个
C.3个
D.4个
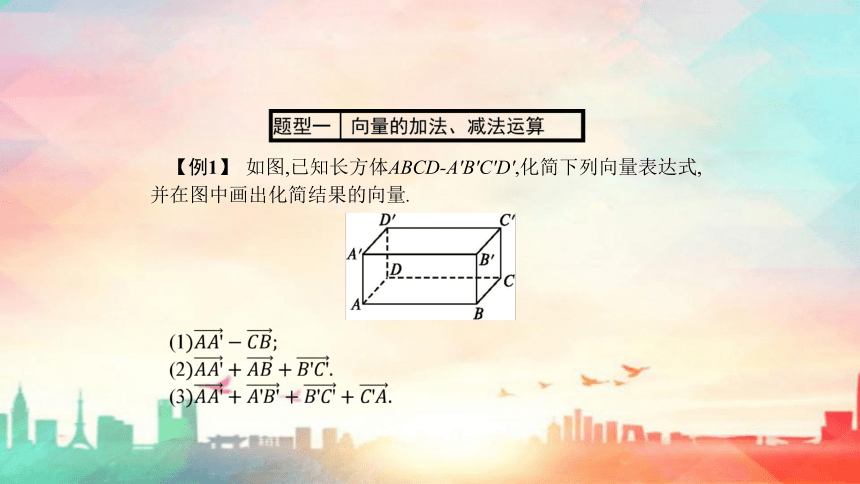
【例1】
如图,已知长方体ABCD-A'B'C'D',化简下列向量表达式,并在图中画出化简结果的向量.
反思运用法则进行向量的线性运算时要注意关键的要素:
(1)向量加法的三角形法则:“首尾相接,指向终点”;
(2)向量减法的三角形法则:“起点重合,指向被减向量”;
(3)平行四边形法则:“起点重合”;
(4)多边形法则:“首尾相接,指向终点”.
运算律
与平面向量一样,空间向量的线性运算满足以下运算律((λ∈R,μ∈R):
(1)结合律 (a+b)+c=a+(b+c);
(2)交换律 a+b=b+a.
(3)分配律
λ(a+b)=λa+λb,(λ+μ)a=λa+μa(λ∈R,μ∈R);
说明:空间向量的加法、减法运算满足平行四边形法则或三角形法则,并且空间向量的加法满足交换律和结合律.
答案:0
反思数乘向量的运算一般是结合所给几何体,联系数乘向量的几何意义转化为一个新的向量.若同时涉及几个数乘向量,则还要注意数乘向量运算律的运用.
共线向量定理:
空间两个向量a与b(b≠0)共线的充要条件是存在实数λ,使得a=λb.
说明:向量共线的充要条件强调b为非零向量,若b为零向量,则a=λb中的a只能为0,没有研究的意义.
探究
【做一做3】
若非零空间向量e1,e2不共线,则使2ke1-e2与e1+2(k+1)e2共线的k的值为 .?
解析:由题可知,2ke1-e2≠0,且e1+2(k+1)e2≠0.
若2ke1-e2与e1+2(k+1)e2共线,则存在实数λ,
使得2ke1-e2=λ[e1+2(k+1)e2]成立.
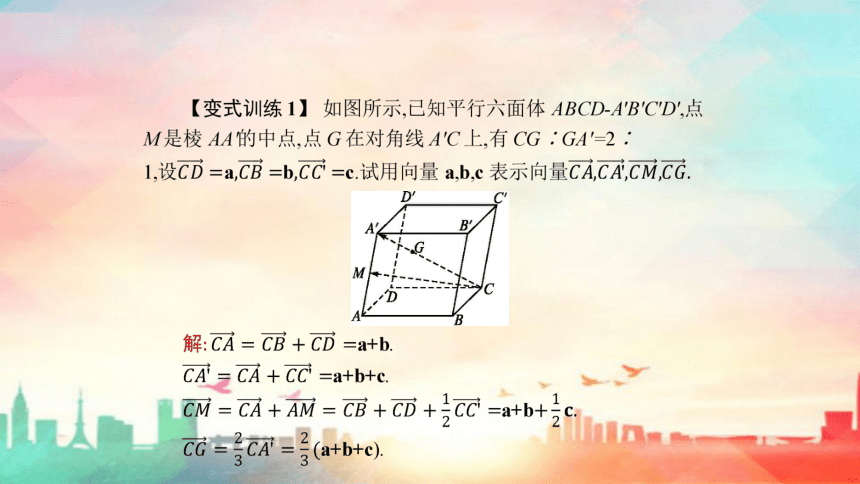
解:如图,取AC的中点记为G,连接EG,FG,
思考:我们知道,任意两个空间向量总是共面的,但三个空间向量既可能是共面的,也可能是不共面的。那么,什么情况下三个空间向量共面呢?
在立体几何的学习中我们学习了异面直线与共面直线,那么向量之间有没有共面的情况呢?
如果直线OA平行于平面α或在平面α内,那么称向量a平行于平面α。平行于同一平面的向量,叫做共面向量。
探究:
题型四、向量共面问题
1.设a,b是两个不共线的向量,λ,μ∈R,若λa+μb=0,则( )
A.a=b=0
B.λ=μ=0
C.λ=0,b=0
D.μ=0,a=0
解析:∵a,b是两个不共线的向量,
∴a≠0,b≠0,
故只有B正确.
答案:B
第二课时 空间向量的数量积运算
物理中,我们学习了力做功的计算方法.如图所示,一辆小车在力F的作用下向前移动了s个单位长度,力与小车前进方向的夹角为θ,那么力作的功W=|F|·|s|cos
θ,这是一个具体的数,可以为正,为负,也可以为零.
一、空间向量的夹角
名师点析1.由定义知,只有两个非零空间向量才有夹角,当两个非零空间向量共线同向时,夹角为0,共线反向时,夹角为π.
2.对空间任意两个非零向量a,b有:
①=;②<-a,b>==π-;③<-a,-b>=.
∠AOB
[0,π]
a⊥b
微练习
在正四面体ABCD中,
的夹角等于( )
A.30°
B.60°
C.150°
D.120°
答案:D
二、空间向量的数量积
1.定义:已知两个非零向量a,b,则
叫做a,b的数量积,记作 .?
即a·b=|a||b|cos.
特别地,零向量与任意向量的数量积为 .?
2.数量积的运算性质
a·e=|a|cos(e为单位向量)
若a,b是非零向量,则a⊥b?a·b=0
若a与b同向,则a·b=|a||b|;
若a与b反向,则a·b=-|a||b|.
|a·b|≤|a||b|(当且仅当a,b共线时等号成立)
|a||b|cos
a·b
0
3.向量a在向量b上的投影向量
在空间,向量a向向量b投影,得到与向量b共线的向量c,c=|a|cos
称为向量a在向量b上的投影向量.
5.数量积的运算律:
(λa)·b= ;a·b= (交换律);?
a·(b+c)= (分配律).
λ(a·b)
b·a
a·b+a·c
名师点析1.对空间向量数量积的理解
(1)两个空间向量的数量积是数量,而不是向量,它可以是正数、负数或零;
(2)空间向量的数量积运算不满足消去律和结合律,即a·b=a·c?b=c,(a·b)·c=a·(b·c)都不成立.
量夹角,特别是两异面直线夹角的问题;
(3)利用关系a⊥b?a·b=0可以证明空间两直线的垂直.
微练习1
答案:C
微判断
对不为0的三个实数a,b,c,有(ab)c=a(bc)成立,所以对三个非零向量a,b,c,也有(a·b)c=a(b·c)成立.( )
微练习2
已知空间向量a,b的夹角为120°,且|a|=1,|b|=2,
则a·(2a-3b)= .?
×
答案:
5
求空间向量的数量积
例1已知三棱锥O-ABC的各个侧面都是等边三角形,且边长为2,点M,N,P分别为AB,BC,CA的中点.试求:
思路分析求出每个向量的模及它们的夹角,然后按照数量积的定义求解,必要时,对向量进行分解.
反思感悟空间向量运算的方法与步骤
方法:(1)利用定义,直接利用a·b=|a||b|cos并结合运算律进行计算.
(2)利用图形,计算两个向量的数量积,可先将各向量移到同一顶点,利用图形寻找夹角,再代入数量积公式进行运算.
(3)利用向量分解,在几何体中进行向量的数量积运算时,要充分利用几何体的性质,把待求向量用已知夹角和模的向量表示后再进行运算.
步骤:(1)首先将各向量分解成已知模和夹角的向量的线性组合形式;
(2)利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积;
(3)代入a·b=|a||b|cos求解.
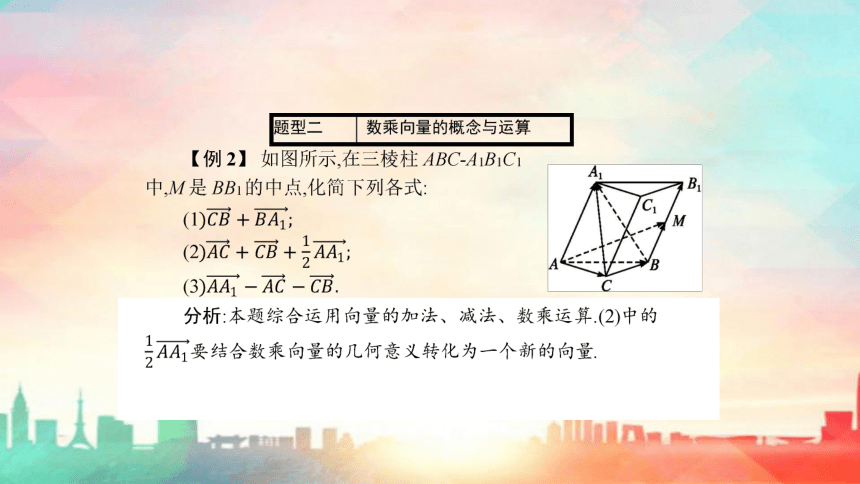
解析:如图,连接AG并延长,与BC交于点D,
∵点G是底面△ABC的重心,
利用数量积求夹角
思路分析求两个向量的夹角,可以把其中一个向量平移到与另一个向量的起点重合,从而转化为求平面角的大小;也可以用两个向量的数量积定义a·b=|a||b|cos,求出cos=
的值,然后确定的大小.
反思感悟两个非零向量夹角求法的两个途径
(1)转化求角:把向量夹角转化为平面几何中的对应角,利用解三角形的知识求解;
变式训练2(1)若非零空间向量a,b满足|a|=|b|,(2a+b)·b=0,则a与b的夹角为( )
A.30°
B.60°
C.120°
D.150°
答案:C
解析:设a与b的夹角为θ,则由(2a+b)·b=0,得2|a||b|cos
θ+|b|2=0.
(2)已知空间四面体OABC各边及对角线长都等于2,E,F分别为AB,OC的中点,则向量
所成角的余弦值为 .?
利用数量积证明垂直问题
例3如图,在正方体ABCD-A1B1C1D1中,P是DD1的中点,O是底面ABCD的中心.求证:OB1⊥平面PAC.
反思感悟利用数量积证明垂直问题的一般方法
将所证垂直问题转化为证明线线垂直,然后把直线转化为向量,并用已知向量表示未知向量,然后通过向量的线性运算以及数量积运算,证明直线所在向量的数量积等于零,即可证明线线垂直.
变式训练3已知空间四边形OABC中,M,N,P,Q分别为BC,AC,OA,OB的中点,若AB=OC,求证:PM⊥QN.
利用数量积求距离或长度
例4如图所示,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,沿着它的对角线AC将△ACD折起,使AB与CD成60°角,求此时B,D间的距离.
反思感悟求两点间的距离或线段长度的方法
(1)将此线段用向量表示;
(2)用其他已知夹角和模的向量表示该向量;
变式训练4正三棱柱ABC-A1B1C1的各棱长都为2,E,F分别是AB,A1C1的中点,则EF的长是( )
答案:C
利用向量的数量积求两异面直线所成角
典例如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,
AA1=
,求异面直线BA1与AC所成角的余弦值.
【答题模板】
第1步:确定两两垂直的向量,把待求直线看作向量,用相关向量表示.
?
第2步:计算直线BA1与AC对应向量的数量积.
?
第3步:利用数量积公式计算两个向量夹角的余弦值.
?
第4步:将两向量夹角的余弦值转化为两直线夹角的余弦值.
失误警示通过阅卷统计分析,发现造成失分的原因主要如下:
(1)解题时忽视条件∠ABC=90°,从而得不出两两垂直的向量;
1.在正方体ABCD-A1B1C1D1中,下列各对向量夹角为45°的是( )
答案:A
解析:四个选项中两个向量的夹角依次是45°,135°,90°,180°,故选A.
答案:D
3.在正方体ABCD-A1B1C1D1中,E是上底面A1B1C1D1的中心,则AC1与CE的位置关系是( )
A.重合
B.平行
C.垂直
D.无法确定
答案:C
4.如图,在长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E,F,G分别是DC,AB,CC1的中点,则异面直线A1E与GF所成角的余弦值是( )
答案:A
5.如图所示,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°,求证:CC1⊥BD.
第1课时 空间向量的线性运算
重难点:1.会用图形说明空间向量加法、减法、数
乘向量及它们的运算律.
2.能运用空间向量的运算意义及运算律解
决简单的立体几何问题.
与平面向量一样:
一、空间向量的概念
(1)向量:在空间中,具_________和______的量.
(2)向量a的长度或模:表示向量a的有向线段的长度,记作|a|.
(3)零向量:长度为______的向量。(手写记作
)
单位向量:长度为_______的向量。
(4)相等向量:在空间,方向相同且模相等的向量。
(5)相反向量:长度_______方向________的向量。
(6)共线向量或平行向量:如果表示若干空间向量的有向线段所在的直线互相平行或重合。
规定:零向量与任意向量共线.
大小
方向
做一做1、正方体ABCD
-
A'B'C'D'中与向量相等的向量有_____
1
相等
相反
0
3
已知空间向量
,以任意点O为起点
,作向量
,我们就可以把他们平移到同一平面
,这样任意的两个空间向量的运算就可以转化为平面向量运算。由此,我们把平面向量的运算推广到空间,定义空间向量的加减法以及数乘运算:
A.1个
B.2个
C.3个
D.4个
【例1】
如图,已知长方体ABCD-A'B'C'D',化简下列向量表达式,并在图中画出化简结果的向量.
反思运用法则进行向量的线性运算时要注意关键的要素:
(1)向量加法的三角形法则:“首尾相接,指向终点”;
(2)向量减法的三角形法则:“起点重合,指向被减向量”;
(3)平行四边形法则:“起点重合”;
(4)多边形法则:“首尾相接,指向终点”.
运算律
与平面向量一样,空间向量的线性运算满足以下运算律((λ∈R,μ∈R):
(1)结合律 (a+b)+c=a+(b+c);
(2)交换律 a+b=b+a.
(3)分配律
λ(a+b)=λa+λb,(λ+μ)a=λa+μa(λ∈R,μ∈R);
说明:空间向量的加法、减法运算满足平行四边形法则或三角形法则,并且空间向量的加法满足交换律和结合律.
答案:0
反思数乘向量的运算一般是结合所给几何体,联系数乘向量的几何意义转化为一个新的向量.若同时涉及几个数乘向量,则还要注意数乘向量运算律的运用.
共线向量定理:
空间两个向量a与b(b≠0)共线的充要条件是存在实数λ,使得a=λb.
说明:向量共线的充要条件强调b为非零向量,若b为零向量,则a=λb中的a只能为0,没有研究的意义.
探究
【做一做3】
若非零空间向量e1,e2不共线,则使2ke1-e2与e1+2(k+1)e2共线的k的值为 .?
解析:由题可知,2ke1-e2≠0,且e1+2(k+1)e2≠0.
若2ke1-e2与e1+2(k+1)e2共线,则存在实数λ,
使得2ke1-e2=λ[e1+2(k+1)e2]成立.
解:如图,取AC的中点记为G,连接EG,FG,
思考:我们知道,任意两个空间向量总是共面的,但三个空间向量既可能是共面的,也可能是不共面的。那么,什么情况下三个空间向量共面呢?
在立体几何的学习中我们学习了异面直线与共面直线,那么向量之间有没有共面的情况呢?
如果直线OA平行于平面α或在平面α内,那么称向量a平行于平面α。平行于同一平面的向量,叫做共面向量。
探究:
题型四、向量共面问题
1.设a,b是两个不共线的向量,λ,μ∈R,若λa+μb=0,则( )
A.a=b=0
B.λ=μ=0
C.λ=0,b=0
D.μ=0,a=0
解析:∵a,b是两个不共线的向量,
∴a≠0,b≠0,
故只有B正确.
答案:B
第二课时 空间向量的数量积运算
物理中,我们学习了力做功的计算方法.如图所示,一辆小车在力F的作用下向前移动了s个单位长度,力与小车前进方向的夹角为θ,那么力作的功W=|F|·|s|cos
θ,这是一个具体的数,可以为正,为负,也可以为零.
一、空间向量的夹角
名师点析1.由定义知,只有两个非零空间向量才有夹角,当两个非零空间向量共线同向时,夹角为0,共线反向时,夹角为π.
2.对空间任意两个非零向量a,b有:
①
∠AOB
[0,π]
a⊥b
微练习
在正四面体ABCD中,
的夹角等于( )
A.30°
B.60°
C.150°
D.120°
答案:D
二、空间向量的数量积
1.定义:已知两个非零向量a,b,则
叫做a,b的数量积,记作 .?
即a·b=|a||b|cos
特别地,零向量与任意向量的数量积为 .?
2.数量积的运算性质
a·e=|a|cos
若a,b是非零向量,则a⊥b?a·b=0
若a与b同向,则a·b=|a||b|;
若a与b反向,则a·b=-|a||b|.
|a·b|≤|a||b|(当且仅当a,b共线时等号成立)
|a||b|cos
a·b
0
3.向量a在向量b上的投影向量
在空间,向量a向向量b投影,得到与向量b共线的向量c,c=|a|cos
称为向量a在向量b上的投影向量.
5.数量积的运算律:
(λa)·b= ;a·b= (交换律);?
a·(b+c)= (分配律).
λ(a·b)
b·a
a·b+a·c
名师点析1.对空间向量数量积的理解
(1)两个空间向量的数量积是数量,而不是向量,它可以是正数、负数或零;
(2)空间向量的数量积运算不满足消去律和结合律,即a·b=a·c?b=c,(a·b)·c=a·(b·c)都不成立.
量夹角,特别是两异面直线夹角的问题;
(3)利用关系a⊥b?a·b=0可以证明空间两直线的垂直.
微练习1
答案:C
微判断
对不为0的三个实数a,b,c,有(ab)c=a(bc)成立,所以对三个非零向量a,b,c,也有(a·b)c=a(b·c)成立.( )
微练习2
已知空间向量a,b的夹角为120°,且|a|=1,|b|=2,
则a·(2a-3b)= .?
×
答案:
5
求空间向量的数量积
例1已知三棱锥O-ABC的各个侧面都是等边三角形,且边长为2,点M,N,P分别为AB,BC,CA的中点.试求:
思路分析求出每个向量的模及它们的夹角,然后按照数量积的定义求解,必要时,对向量进行分解.
反思感悟空间向量运算的方法与步骤
方法:(1)利用定义,直接利用a·b=|a||b|cos
(2)利用图形,计算两个向量的数量积,可先将各向量移到同一顶点,利用图形寻找夹角,再代入数量积公式进行运算.
(3)利用向量分解,在几何体中进行向量的数量积运算时,要充分利用几何体的性质,把待求向量用已知夹角和模的向量表示后再进行运算.
步骤:(1)首先将各向量分解成已知模和夹角的向量的线性组合形式;
(2)利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积;
(3)代入a·b=|a||b|cos
解析:如图,连接AG并延长,与BC交于点D,
∵点G是底面△ABC的重心,
利用数量积求夹角
思路分析求两个向量的夹角,可以把其中一个向量平移到与另一个向量的起点重合,从而转化为求平面角的大小;也可以用两个向量的数量积定义a·b=|a||b|cos
的值,然后确定
反思感悟两个非零向量夹角求法的两个途径
(1)转化求角:把向量夹角转化为平面几何中的对应角,利用解三角形的知识求解;
变式训练2(1)若非零空间向量a,b满足|a|=|b|,(2a+b)·b=0,则a与b的夹角为( )
A.30°
B.60°
C.120°
D.150°
答案:C
解析:设a与b的夹角为θ,则由(2a+b)·b=0,得2|a||b|cos
θ+|b|2=0.
(2)已知空间四面体OABC各边及对角线长都等于2,E,F分别为AB,OC的中点,则向量
所成角的余弦值为 .?
利用数量积证明垂直问题
例3如图,在正方体ABCD-A1B1C1D1中,P是DD1的中点,O是底面ABCD的中心.求证:OB1⊥平面PAC.
反思感悟利用数量积证明垂直问题的一般方法
将所证垂直问题转化为证明线线垂直,然后把直线转化为向量,并用已知向量表示未知向量,然后通过向量的线性运算以及数量积运算,证明直线所在向量的数量积等于零,即可证明线线垂直.
变式训练3已知空间四边形OABC中,M,N,P,Q分别为BC,AC,OA,OB的中点,若AB=OC,求证:PM⊥QN.
利用数量积求距离或长度
例4如图所示,在平行四边形ABCD中,AB=AC=1,∠ACD=90°,沿着它的对角线AC将△ACD折起,使AB与CD成60°角,求此时B,D间的距离.
反思感悟求两点间的距离或线段长度的方法
(1)将此线段用向量表示;
(2)用其他已知夹角和模的向量表示该向量;
变式训练4正三棱柱ABC-A1B1C1的各棱长都为2,E,F分别是AB,A1C1的中点,则EF的长是( )
答案:C
利用向量的数量积求两异面直线所成角
典例如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1,
AA1=
,求异面直线BA1与AC所成角的余弦值.
【答题模板】
第1步:确定两两垂直的向量,把待求直线看作向量,用相关向量表示.
?
第2步:计算直线BA1与AC对应向量的数量积.
?
第3步:利用数量积公式计算两个向量夹角的余弦值.
?
第4步:将两向量夹角的余弦值转化为两直线夹角的余弦值.
失误警示通过阅卷统计分析,发现造成失分的原因主要如下:
(1)解题时忽视条件∠ABC=90°,从而得不出两两垂直的向量;
1.在正方体ABCD-A1B1C1D1中,下列各对向量夹角为45°的是( )
答案:A
解析:四个选项中两个向量的夹角依次是45°,135°,90°,180°,故选A.
答案:D
3.在正方体ABCD-A1B1C1D1中,E是上底面A1B1C1D1的中心,则AC1与CE的位置关系是( )
A.重合
B.平行
C.垂直
D.无法确定
答案:C
4.如图,在长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E,F,G分别是DC,AB,CC1的中点,则异面直线A1E与GF所成角的余弦值是( )
答案:A
5.如图所示,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°,求证:CC1⊥BD.
