人教A版(2019)选择性必修 第一册第三章 圆锥曲线的方程3.1椭圆(共72张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修 第一册第三章 圆锥曲线的方程3.1椭圆(共72张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-26 21:03:02 | ||
图片预览










文档简介
(共72张PPT)
3.1.1 椭圆及其标准方程
《今日美国》2018年12月9日报道,“天文爱好者们即将看到一个惊喜,名为‘46P/Wirtanen’的彗星,即将成为1950年以来最接近地球的10颗彗星之一.‘46P/Wirtanen’会在美国时间12月16日最接近地球.届时,这颗彗星将“仅”距离地球710万英里(从天文的角度来说,这已经很近了).在此期间,这颗彗星应该肉眼可见.”
天文学家是如何计算出彗星出现的准确时间呢?
原来,这颗彗星运行的轨道是一个椭圆,通过观察它运行中的一些有关数据,可以推算出它的运行轨道的方程,从而算出它运行的周期及轨道的周长,预测它接近地球或离去的时间.
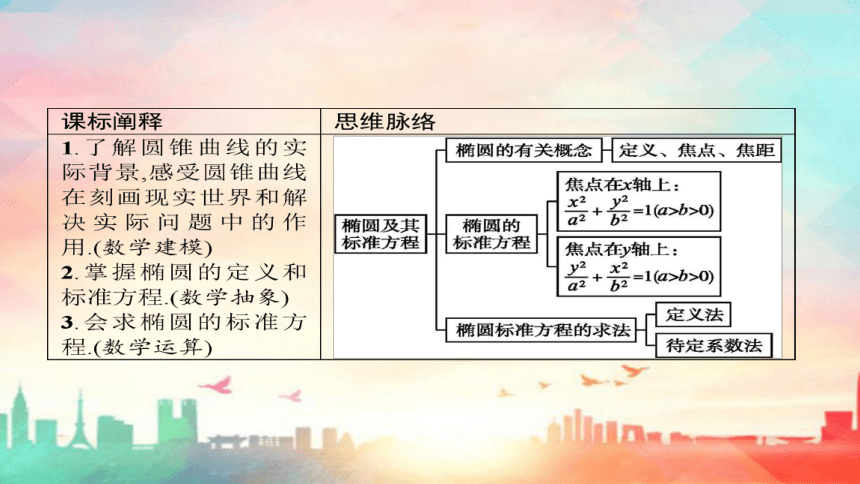
一、椭圆的定义
1.定义
我们把平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距,焦距的一半称为半焦距.
2.定义的集合语言表述
集合P={M||MF1|+|MF2|=2a,2a>|F1F2|}.
名师点析在椭圆定义中,要求常数必须大于两定点F1,F2之间的距离,这是椭圆定义中非常重要的一个条件,可以验证:如果这个常数等于两定点F1,F2之间的距离,动点的轨迹将是一条线段;如果这个常数小于两定点F1,F2之间的距离,动点的轨迹将不存在.因此在根据椭圆定义判断动点的轨迹时,务必注意这一隐含的条件.
微练习
下列说法中,正确的是( )
A.到点M(-3,0),N(3,0)的距离之和等于4的点的轨迹是椭圆
B.到点M(0,-3),N(0,3)的距离之和等于6的点的轨迹是椭圆
C.到点M(-3,0),N(3,0)的距离之和等于8的点的轨迹是椭圆
D.到点M(0,-3),N(0,3)的距离相等的点的轨迹是椭圆
答案:C
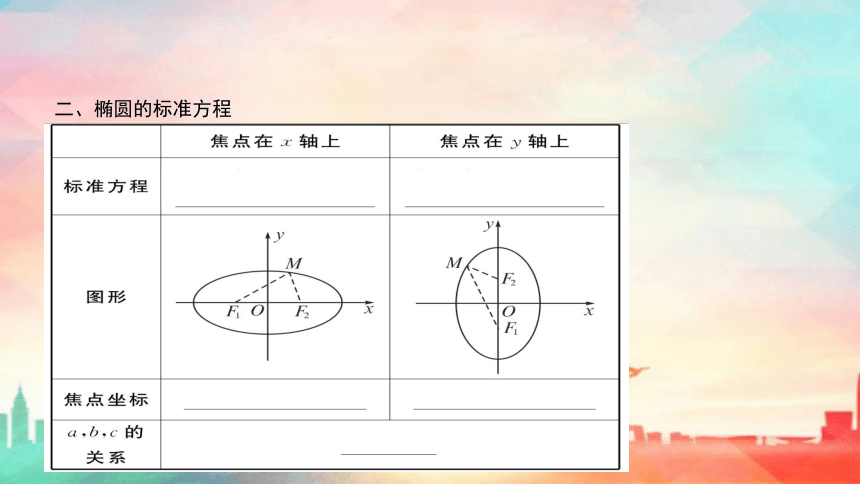
二、椭圆的标准方程
0
0
0
名师点析1.椭圆的标准方程是指当椭圆在标准位置时的方程,所谓标准位置,就是指椭圆的中心在坐标原点,椭圆的对称轴为坐标轴.
(2)已知a=5,c=2,焦点在y轴上,则椭圆的标准方程为 .?
解析:(1)因为10>6,所以焦点在x轴上,且a2=10,b2=6,
所以c2=10-6=4,c=2,故焦点坐标为(2,0)和(-2,0).
求椭圆的标准方程
1.待定系数法
例1根据下列条件,求椭圆的标准方程:
(1)两个焦点的坐标分别为(-4,0)和(4,0),且椭圆经过点(5,0);
(2)焦点在y轴上,且经过两个点(0,2)和(1,0);
思路分析:(1)设出焦点在x轴上的椭圆的标准方程,再根据条件求出a,b的值,即可求得方程;(2)设出焦点在y轴上的椭圆的标准方程,再根据条件求出a,b的值,即可求得方程;(3)焦点位置不确定,可以分两种情况分别求解,也可直接设所求椭圆方程为mx2+ny2=1(m>0,n>0,m≠n).
反思感悟椭圆方程的求法
1.利用待定系数法求椭圆标准方程的一般步骤如下:
(1)先确定焦点位置;(2)设出方程;(3)寻求a,b,c的等量关系;(4)求a,b的值,代入所设方程.
2.当焦点位置不确定时,可设椭圆方程为mx2+ny2=1(m≠n,m>0,n>0).因为焦点位置包括焦点在x轴上(mn)两种情况,所以可以避免分类讨论,从而简化运算.
变式训练1根据下列条件,求椭圆的标准方程.
(2)经过点(2,-3)且与椭圆9x2+4y2=36有共同的焦点.
2.定义法
例2一个动圆与圆Q1:(x+3)2+y2=1外切,与圆Q2:(x-3)2+y2=81内切,试求这个动圆圆心的轨迹方程.
思路分析:两圆相切时,圆心之间的距离与两圆的半径有关,由此可以找到动圆圆心满足的条件等式.
解:两定圆的圆心和半径分别为Q1(-3,0),r1=1;Q2(3,0),r2=9.
设动圆圆心为M(x,y),半径为R,由题意有|MQ1|=1+R,|MQ2|=9-R,
∴|MQ1|+|MQ2|=10>|Q1Q2|=6.
由椭圆的定义可知点M在以Q1,Q2为焦点的椭圆上,且a=5,c=3,∴b2=a2-c2=25-9=16.
反思感悟1.若动点轨迹满足椭圆的定义,则根据椭圆的定义来确定a,b,c,从而确定椭圆的标准方程,这种求轨迹方程的方法称为定义法.
2.一般步骤:
(1)将条件转化为到两定点的距离之和为定值(该定值大于两定点之间的距离);
(2)判断椭圆的中心是否在原点、对称轴是否为坐标轴;
(3)确定椭圆的基本量a,b,c,从而确定椭圆的标准方程.
延伸探究本题两个已知圆不变,若动圆与两个圆都内切,求动圆圆心的轨迹方程.
解:设动圆圆心为P(x,y),半径为r.
由圆P与圆Q1内切,得|PQ1|=r-1;
由圆P与圆Q2内切,得|PQ2|=9-r.
所以|PQ1|+|PQ2|=8>6=|Q1Q2|.
所以P点轨迹是以Q1,Q2为焦点的椭圆,且2a=8,2c=6.
即a=4,c=3,所以b2=a2-c2=7.
对椭圆标准方程的理解
A.(-9,25)
B.(-9,8)∪(8,25)
C.(8,25)
D.(8,+∞)
(2)若方程x2-3my2=1表示焦点在x轴上的椭圆,则实数m的取值范围是 .?
反思感悟根据椭圆方程求参数的取值范围
答案:(-4,0)∪(0,3)
椭圆中的焦点三角形问题
思路分析:(1)由|PF1|+|PF2|是定值,求|PF1|·|PF2|的最大值,可考虑用基本不等式;(2)求焦点三角形的面积,可考虑用定义|PF1|+|PF2|=2a及余弦定理先求|PF1|·|PF2|,再考虑用三角形面积公式求面积.
当且仅当|PF1|=|PF2|=10时,等号成立,即|PF1|·|PF2|取到最大值100.
(2)c2=a2-b2=100-64=36,c=6,
则F1(-6,0),F2(6,0).∵P为椭圆上任一点,
∴|PF1|+|PF2|=2a=20.
在△PF1F2中,|F1F2|=2c=12,
即122=|PF1|2+|PF2|2-|PF1|·|PF2|.
∵|PF1|2+|PF2|2=(|PF1|+|PF2|)2-2|PF1|·|PF2|,
∴122=(|PF1|+|PF2|)2-3|PF1|·|PF2|,
∴122=202-3|PF1|·|PF2|,
反思感悟1.焦点三角形的概念
如图,设M是椭圆上一点,F1,F2为椭圆的焦点,当点M,F1,F2不在同一条直线上时,它们构成一个三角形——焦点三角形.
2.关于椭圆的焦点三角形问题,可结合椭圆的定义列出|PF1|+|PF2|=2a,利用这个关系式转化求解.因此回归定义是求解椭圆的焦点三角形问题的常用方法.在求解过程中要灵活运用勾股定理、正弦定理、余弦定理等.
3.焦点三角形的常用公式
(1)焦点三角形的周长L=2a+2c.
(2)在△MF1F2中,由余弦定理可得
|F1F2|2=|MF1|2+|MF2|2-2|MF1||MF2|cos
θ.
垂直于x轴,交椭圆于A,B两点,F1是椭圆的左焦点.
(1)求△AF1B的周长.
(2)如果AB不垂直于x轴,△AF1B的周长有变化吗?为什么?
故有|AF1|+|AF2|=2a=10,|BF1|+|BF2|=2a=10,|AF2|+|BF2|=|AB|,
∴△AF1B的周长=|AF1|+|BF1|+|AB|=|AF1|+|BF1|+|AF2|+|BF2|
=(|AF1|+|AF2|)+(|BF1|+|BF2|)=2a+2a=10+10=20,
∴△AF1B的周长为20.
(2)如果AB不垂直于x轴,△AF1B的周长仍为20不变.
理由:|AF1|+|BF1|+|AB|=|AF1|+|BF1|+|AF2|+|BF2|
=(|AF1|+|AF2|)+(|BF1|+|BF2|)=4a,和AB与x轴是否垂直无关.
求与椭圆有关的轨迹问题
典例已知B,C是两个定点,|BC|=8,且△ABC的周长等于18.求这个三角形的顶点A的轨迹方程.
解:以过B,C两点的直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系xOy,如图所示.
由|BC|=8可知点B(-4,0),C(4,0).
由|AB|+|AC|+|BC|=18,
得|AB|+|AC|=10>8=|BC|,
因此,点A的轨迹是以B,C为焦点的椭圆,这个椭圆上的点与两焦点的距离之和2a=10,焦距2c=8,但点A不在x轴上.
由a=5,c=4,
得b2=a2-c2=25-16=9.
方法总结求与椭圆有关的轨迹方程常用的方法
(1)定义法:若动点的轨迹特点符合某一基本轨迹(如椭圆、圆等)的定义,则可用定义直接求解.
(2)直接法:将动点满足的几何条件或者等量关系直接坐标化,列出等式后化简,得出动点的轨迹方程.
(3)相关点法:根据相关点所满足的方程,通过转换求出动点轨迹的方程.
1.已知F1,F2为两定点,|F1F2|=6,动点M满足|MF1|+|MF2|=16,则动点M的轨迹是( )
A.椭圆
B.直线
C.圆
D.线段
解析:因为|MF1|+|MF2|=16>|F1F2|,所以动点M的轨迹是椭圆.
答案:A
2.椭圆的两个焦点分别为F1(-8,0),F2(8,0),且椭圆上一点到两个焦点的距离之和为20,则此椭圆的标准方程为( )
答案:C
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:B
答案:6
5.求以椭圆9x2+5y2=45的焦点为焦点,且经过点M(2,
)的椭圆的标准方程.
3.1.2 椭圆的简单几何性质
地球围绕太阳公转的轨道是一个椭圆,太阳处在这个椭圆的一个焦点上.在椭圆轨道上有一个近日点和一个远日点,在近日点时距离太阳14
710万千米,在远日点时距离太阳15
210万千米.事实上,很多天体或飞行器的运行轨道都是椭圆.如神舟九号飞船,于2012年6月16日搭载3名航天员发射升空,之后进入近地点高度200千米,远地点高度329.8千米的椭圆形轨道,然后进行了5次变轨,两天后与天宫一号自动交会对接成功,这是中国首次实现载人空间交会对接任务.
椭圆的简单几何性质
名师点拨1.椭圆的范围给出了椭圆上的点的横坐标、纵坐标的取值范围,在求解一些存在性、判断性问题中有着重要的应用,也可用于求最值、求轨迹等问题时的检验等.
2.利用方程研究曲线对称性的方法如下:
(1)若把曲线方程中的x换成-x,方程不变,则曲线关于y轴对称;
(2)若把曲线方程中的y换成-y,方程不变,则曲线关于x轴对称;
(3)若同时把曲线方程中的x换成-x,y换成-y,方程不变,则曲线关于原点对称.
微练习
(1)已知椭圆
=1,则其顶点坐标分别为 ,焦点坐标为 ,长轴长等于 ,短轴长等于 ,焦距等于 .若点P(m,n)为该椭圆上任意一点,则m的取值范围是 .?
(2)椭圆x2+4y2=1的离心率等于( )
答案:A
根据椭圆的标准方程研究其几何性质
例1求椭圆9x2+16y2=144的长轴长、短轴长、离心率、焦点和顶点坐标.
延伸探究本例中若把椭圆方程改为“9x2+16y2=1”,求其长轴长、短轴长、离心率、焦点和顶点坐标.
反思感悟确定椭圆几何性质的基本步骤
(1)化标准,把椭圆方程化成标准形式;
(2)定位置,根据标准方程中x2,y2对应分母的大小来确定焦点位置;
(3)求参数,写出a,b的值,并求出c的值;
(4)写性质,按要求写出椭圆的简单几何性质.
长、短轴长分别相等,且椭圆C2的焦点在y轴上.
(1)求椭圆C1的长半轴长、短半轴长、焦点坐标及离心率;
(2)写出椭圆C2的方程,并研究其性质.
根据椭圆的几何性质求其标准方程
例2根据下列条件求椭圆的标准方程:
(2)在x轴上的一个焦点,与短轴两个端点的连线互相垂直,且焦距为8.
思路分析:(1)焦点位置不确定,应分类讨论;(2)结合图形求出a,b,c的值代入.
如图所示,△A1FA2为等腰直角三角形,
OF为斜边A1A2的中线(高),
且|OF|=c,|A1A2|=2b,
∴c=b=4,∴a2=b2+c2=32.
反思感悟根据椭圆的性质求方程
1.已知椭圆的几何性质,求其标准方程主要采用待定系数法,解题步骤为:
(1)确定焦点所在的位置,以确定椭圆标准方程的形式;
(2)确立关于a,b,c的方程(组),求出参数a,b,c;
(3)写出标准方程.
2.在求椭圆方程时,要注意根据题目条件判断焦点所在的坐标轴,从而确定方程的形式,若不能确定焦点所在坐标轴,则应进行讨论.一般地,已知椭圆的焦点坐标时,可以确定焦点位置,而已知离心率、长轴长、短轴长、焦距时,则不能确定焦点位置.
变式训练2已知椭圆的长轴长是短轴长的2倍,且经过点A(2,0),求椭圆的标准方程.
求椭圆的离心率的值(或范围)
(方法2)设A(0,b),B(a,0),F(-c,0),
设△FAB的外接圆的方程为x2+y2+Dx+Ey+F=0.
将A,B,F三点的坐标分别代入外接圆方程,
答案:(1)A (2)A
反思感悟求椭圆离心率及取值范围的两种方法
(2)方程法:若a,c的值不可求,则可根据条件建立a,b,c的关系式,借助于a2=b2+c2,转化为关于a,c的齐次方程或不等式,再将方程或不等式两边同除以a的最高次幂,得到关于e的方程或不等式,即可求得e的值或范围.求离心率的范围时,应根据题意建立a,c的不等式,结合e∈(0,1)确定离心率的范围.
变式训练3(1)已知椭圆的焦距不小于短轴长,求椭圆的离心率的取值范围.
(2)如图所示,设直线y=2x与椭圆的一个交点为P,
则点P横坐标为c,连接PF1,PF2,则|PF1|=2c.
因为△PF1F2为直角三角形,|F1F2|=2c,
反思感悟离心率的求法
(3)若已知a,b,c的关系,则可转化为a,c的方程或不等式,进而得到关于e的方程或不等式进行求解.
一题多变——求椭圆的离心率
答案:D
变式训练1(变条件)若将本例中“PF2⊥F1F2,∠PF1F2=30°”改为“∠PF2F1=75°,∠PF1F2=45°”,求椭圆C的离心率.
解:在△PF1F2中,
∵∠PF1F2=45°,∠PF2F1=75°,
∴∠F1PF2=60°,
设|PF1|=m,|PF2|=n,|F1F2|=2c,椭圆的长轴长为2a,
变式训练2(变条件,变设问)若将本例中“PF2⊥F1F2,∠PF1F2=30°”改为“椭圆C上存在点P,使∠F1PF2为钝角”,求椭圆C的离心率的取值范围.
1.椭圆6x2+y2=6的长轴的端点坐标是( )
A.(-1,0),(1,0)
B.(0,-1),(0,1)
答案:D
答案:A
答案:A
3.1.1 椭圆及其标准方程
《今日美国》2018年12月9日报道,“天文爱好者们即将看到一个惊喜,名为‘46P/Wirtanen’的彗星,即将成为1950年以来最接近地球的10颗彗星之一.‘46P/Wirtanen’会在美国时间12月16日最接近地球.届时,这颗彗星将“仅”距离地球710万英里(从天文的角度来说,这已经很近了).在此期间,这颗彗星应该肉眼可见.”
天文学家是如何计算出彗星出现的准确时间呢?
原来,这颗彗星运行的轨道是一个椭圆,通过观察它运行中的一些有关数据,可以推算出它的运行轨道的方程,从而算出它运行的周期及轨道的周长,预测它接近地球或离去的时间.
一、椭圆的定义
1.定义
我们把平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.
这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距,焦距的一半称为半焦距.
2.定义的集合语言表述
集合P={M||MF1|+|MF2|=2a,2a>|F1F2|}.
名师点析在椭圆定义中,要求常数必须大于两定点F1,F2之间的距离,这是椭圆定义中非常重要的一个条件,可以验证:如果这个常数等于两定点F1,F2之间的距离,动点的轨迹将是一条线段;如果这个常数小于两定点F1,F2之间的距离,动点的轨迹将不存在.因此在根据椭圆定义判断动点的轨迹时,务必注意这一隐含的条件.
微练习
下列说法中,正确的是( )
A.到点M(-3,0),N(3,0)的距离之和等于4的点的轨迹是椭圆
B.到点M(0,-3),N(0,3)的距离之和等于6的点的轨迹是椭圆
C.到点M(-3,0),N(3,0)的距离之和等于8的点的轨迹是椭圆
D.到点M(0,-3),N(0,3)的距离相等的点的轨迹是椭圆
答案:C
二、椭圆的标准方程
0
0
0
名师点析1.椭圆的标准方程是指当椭圆在标准位置时的方程,所谓标准位置,就是指椭圆的中心在坐标原点,椭圆的对称轴为坐标轴.
(2)已知a=5,c=2,焦点在y轴上,则椭圆的标准方程为 .?
解析:(1)因为10>6,所以焦点在x轴上,且a2=10,b2=6,
所以c2=10-6=4,c=2,故焦点坐标为(2,0)和(-2,0).
求椭圆的标准方程
1.待定系数法
例1根据下列条件,求椭圆的标准方程:
(1)两个焦点的坐标分别为(-4,0)和(4,0),且椭圆经过点(5,0);
(2)焦点在y轴上,且经过两个点(0,2)和(1,0);
思路分析:(1)设出焦点在x轴上的椭圆的标准方程,再根据条件求出a,b的值,即可求得方程;(2)设出焦点在y轴上的椭圆的标准方程,再根据条件求出a,b的值,即可求得方程;(3)焦点位置不确定,可以分两种情况分别求解,也可直接设所求椭圆方程为mx2+ny2=1(m>0,n>0,m≠n).
反思感悟椭圆方程的求法
1.利用待定系数法求椭圆标准方程的一般步骤如下:
(1)先确定焦点位置;(2)设出方程;(3)寻求a,b,c的等量关系;(4)求a,b的值,代入所设方程.
2.当焦点位置不确定时,可设椭圆方程为mx2+ny2=1(m≠n,m>0,n>0).因为焦点位置包括焦点在x轴上(m
变式训练1根据下列条件,求椭圆的标准方程.
(2)经过点(2,-3)且与椭圆9x2+4y2=36有共同的焦点.
2.定义法
例2一个动圆与圆Q1:(x+3)2+y2=1外切,与圆Q2:(x-3)2+y2=81内切,试求这个动圆圆心的轨迹方程.
思路分析:两圆相切时,圆心之间的距离与两圆的半径有关,由此可以找到动圆圆心满足的条件等式.
解:两定圆的圆心和半径分别为Q1(-3,0),r1=1;Q2(3,0),r2=9.
设动圆圆心为M(x,y),半径为R,由题意有|MQ1|=1+R,|MQ2|=9-R,
∴|MQ1|+|MQ2|=10>|Q1Q2|=6.
由椭圆的定义可知点M在以Q1,Q2为焦点的椭圆上,且a=5,c=3,∴b2=a2-c2=25-9=16.
反思感悟1.若动点轨迹满足椭圆的定义,则根据椭圆的定义来确定a,b,c,从而确定椭圆的标准方程,这种求轨迹方程的方法称为定义法.
2.一般步骤:
(1)将条件转化为到两定点的距离之和为定值(该定值大于两定点之间的距离);
(2)判断椭圆的中心是否在原点、对称轴是否为坐标轴;
(3)确定椭圆的基本量a,b,c,从而确定椭圆的标准方程.
延伸探究本题两个已知圆不变,若动圆与两个圆都内切,求动圆圆心的轨迹方程.
解:设动圆圆心为P(x,y),半径为r.
由圆P与圆Q1内切,得|PQ1|=r-1;
由圆P与圆Q2内切,得|PQ2|=9-r.
所以|PQ1|+|PQ2|=8>6=|Q1Q2|.
所以P点轨迹是以Q1,Q2为焦点的椭圆,且2a=8,2c=6.
即a=4,c=3,所以b2=a2-c2=7.
对椭圆标准方程的理解
A.(-9,25)
B.(-9,8)∪(8,25)
C.(8,25)
D.(8,+∞)
(2)若方程x2-3my2=1表示焦点在x轴上的椭圆,则实数m的取值范围是 .?
反思感悟根据椭圆方程求参数的取值范围
答案:(-4,0)∪(0,3)
椭圆中的焦点三角形问题
思路分析:(1)由|PF1|+|PF2|是定值,求|PF1|·|PF2|的最大值,可考虑用基本不等式;(2)求焦点三角形的面积,可考虑用定义|PF1|+|PF2|=2a及余弦定理先求|PF1|·|PF2|,再考虑用三角形面积公式求面积.
当且仅当|PF1|=|PF2|=10时,等号成立,即|PF1|·|PF2|取到最大值100.
(2)c2=a2-b2=100-64=36,c=6,
则F1(-6,0),F2(6,0).∵P为椭圆上任一点,
∴|PF1|+|PF2|=2a=20.
在△PF1F2中,|F1F2|=2c=12,
即122=|PF1|2+|PF2|2-|PF1|·|PF2|.
∵|PF1|2+|PF2|2=(|PF1|+|PF2|)2-2|PF1|·|PF2|,
∴122=(|PF1|+|PF2|)2-3|PF1|·|PF2|,
∴122=202-3|PF1|·|PF2|,
反思感悟1.焦点三角形的概念
如图,设M是椭圆上一点,F1,F2为椭圆的焦点,当点M,F1,F2不在同一条直线上时,它们构成一个三角形——焦点三角形.
2.关于椭圆的焦点三角形问题,可结合椭圆的定义列出|PF1|+|PF2|=2a,利用这个关系式转化求解.因此回归定义是求解椭圆的焦点三角形问题的常用方法.在求解过程中要灵活运用勾股定理、正弦定理、余弦定理等.
3.焦点三角形的常用公式
(1)焦点三角形的周长L=2a+2c.
(2)在△MF1F2中,由余弦定理可得
|F1F2|2=|MF1|2+|MF2|2-2|MF1||MF2|cos
θ.
垂直于x轴,交椭圆于A,B两点,F1是椭圆的左焦点.
(1)求△AF1B的周长.
(2)如果AB不垂直于x轴,△AF1B的周长有变化吗?为什么?
故有|AF1|+|AF2|=2a=10,|BF1|+|BF2|=2a=10,|AF2|+|BF2|=|AB|,
∴△AF1B的周长=|AF1|+|BF1|+|AB|=|AF1|+|BF1|+|AF2|+|BF2|
=(|AF1|+|AF2|)+(|BF1|+|BF2|)=2a+2a=10+10=20,
∴△AF1B的周长为20.
(2)如果AB不垂直于x轴,△AF1B的周长仍为20不变.
理由:|AF1|+|BF1|+|AB|=|AF1|+|BF1|+|AF2|+|BF2|
=(|AF1|+|AF2|)+(|BF1|+|BF2|)=4a,和AB与x轴是否垂直无关.
求与椭圆有关的轨迹问题
典例已知B,C是两个定点,|BC|=8,且△ABC的周长等于18.求这个三角形的顶点A的轨迹方程.
解:以过B,C两点的直线为x轴,线段BC的垂直平分线为y轴,建立平面直角坐标系xOy,如图所示.
由|BC|=8可知点B(-4,0),C(4,0).
由|AB|+|AC|+|BC|=18,
得|AB|+|AC|=10>8=|BC|,
因此,点A的轨迹是以B,C为焦点的椭圆,这个椭圆上的点与两焦点的距离之和2a=10,焦距2c=8,但点A不在x轴上.
由a=5,c=4,
得b2=a2-c2=25-16=9.
方法总结求与椭圆有关的轨迹方程常用的方法
(1)定义法:若动点的轨迹特点符合某一基本轨迹(如椭圆、圆等)的定义,则可用定义直接求解.
(2)直接法:将动点满足的几何条件或者等量关系直接坐标化,列出等式后化简,得出动点的轨迹方程.
(3)相关点法:根据相关点所满足的方程,通过转换求出动点轨迹的方程.
1.已知F1,F2为两定点,|F1F2|=6,动点M满足|MF1|+|MF2|=16,则动点M的轨迹是( )
A.椭圆
B.直线
C.圆
D.线段
解析:因为|MF1|+|MF2|=16>|F1F2|,所以动点M的轨迹是椭圆.
答案:A
2.椭圆的两个焦点分别为F1(-8,0),F2(8,0),且椭圆上一点到两个焦点的距离之和为20,则此椭圆的标准方程为( )
答案:C
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:B
答案:6
5.求以椭圆9x2+5y2=45的焦点为焦点,且经过点M(2,
)的椭圆的标准方程.
3.1.2 椭圆的简单几何性质
地球围绕太阳公转的轨道是一个椭圆,太阳处在这个椭圆的一个焦点上.在椭圆轨道上有一个近日点和一个远日点,在近日点时距离太阳14
710万千米,在远日点时距离太阳15
210万千米.事实上,很多天体或飞行器的运行轨道都是椭圆.如神舟九号飞船,于2012年6月16日搭载3名航天员发射升空,之后进入近地点高度200千米,远地点高度329.8千米的椭圆形轨道,然后进行了5次变轨,两天后与天宫一号自动交会对接成功,这是中国首次实现载人空间交会对接任务.
椭圆的简单几何性质
名师点拨1.椭圆的范围给出了椭圆上的点的横坐标、纵坐标的取值范围,在求解一些存在性、判断性问题中有着重要的应用,也可用于求最值、求轨迹等问题时的检验等.
2.利用方程研究曲线对称性的方法如下:
(1)若把曲线方程中的x换成-x,方程不变,则曲线关于y轴对称;
(2)若把曲线方程中的y换成-y,方程不变,则曲线关于x轴对称;
(3)若同时把曲线方程中的x换成-x,y换成-y,方程不变,则曲线关于原点对称.
微练习
(1)已知椭圆
=1,则其顶点坐标分别为 ,焦点坐标为 ,长轴长等于 ,短轴长等于 ,焦距等于 .若点P(m,n)为该椭圆上任意一点,则m的取值范围是 .?
(2)椭圆x2+4y2=1的离心率等于( )
答案:A
根据椭圆的标准方程研究其几何性质
例1求椭圆9x2+16y2=144的长轴长、短轴长、离心率、焦点和顶点坐标.
延伸探究本例中若把椭圆方程改为“9x2+16y2=1”,求其长轴长、短轴长、离心率、焦点和顶点坐标.
反思感悟确定椭圆几何性质的基本步骤
(1)化标准,把椭圆方程化成标准形式;
(2)定位置,根据标准方程中x2,y2对应分母的大小来确定焦点位置;
(3)求参数,写出a,b的值,并求出c的值;
(4)写性质,按要求写出椭圆的简单几何性质.
长、短轴长分别相等,且椭圆C2的焦点在y轴上.
(1)求椭圆C1的长半轴长、短半轴长、焦点坐标及离心率;
(2)写出椭圆C2的方程,并研究其性质.
根据椭圆的几何性质求其标准方程
例2根据下列条件求椭圆的标准方程:
(2)在x轴上的一个焦点,与短轴两个端点的连线互相垂直,且焦距为8.
思路分析:(1)焦点位置不确定,应分类讨论;(2)结合图形求出a,b,c的值代入.
如图所示,△A1FA2为等腰直角三角形,
OF为斜边A1A2的中线(高),
且|OF|=c,|A1A2|=2b,
∴c=b=4,∴a2=b2+c2=32.
反思感悟根据椭圆的性质求方程
1.已知椭圆的几何性质,求其标准方程主要采用待定系数法,解题步骤为:
(1)确定焦点所在的位置,以确定椭圆标准方程的形式;
(2)确立关于a,b,c的方程(组),求出参数a,b,c;
(3)写出标准方程.
2.在求椭圆方程时,要注意根据题目条件判断焦点所在的坐标轴,从而确定方程的形式,若不能确定焦点所在坐标轴,则应进行讨论.一般地,已知椭圆的焦点坐标时,可以确定焦点位置,而已知离心率、长轴长、短轴长、焦距时,则不能确定焦点位置.
变式训练2已知椭圆的长轴长是短轴长的2倍,且经过点A(2,0),求椭圆的标准方程.
求椭圆的离心率的值(或范围)
(方法2)设A(0,b),B(a,0),F(-c,0),
设△FAB的外接圆的方程为x2+y2+Dx+Ey+F=0.
将A,B,F三点的坐标分别代入外接圆方程,
答案:(1)A (2)A
反思感悟求椭圆离心率及取值范围的两种方法
(2)方程法:若a,c的值不可求,则可根据条件建立a,b,c的关系式,借助于a2=b2+c2,转化为关于a,c的齐次方程或不等式,再将方程或不等式两边同除以a的最高次幂,得到关于e的方程或不等式,即可求得e的值或范围.求离心率的范围时,应根据题意建立a,c的不等式,结合e∈(0,1)确定离心率的范围.
变式训练3(1)已知椭圆的焦距不小于短轴长,求椭圆的离心率的取值范围.
(2)如图所示,设直线y=2x与椭圆的一个交点为P,
则点P横坐标为c,连接PF1,PF2,则|PF1|=2c.
因为△PF1F2为直角三角形,|F1F2|=2c,
反思感悟离心率的求法
(3)若已知a,b,c的关系,则可转化为a,c的方程或不等式,进而得到关于e的方程或不等式进行求解.
一题多变——求椭圆的离心率
答案:D
变式训练1(变条件)若将本例中“PF2⊥F1F2,∠PF1F2=30°”改为“∠PF2F1=75°,∠PF1F2=45°”,求椭圆C的离心率.
解:在△PF1F2中,
∵∠PF1F2=45°,∠PF2F1=75°,
∴∠F1PF2=60°,
设|PF1|=m,|PF2|=n,|F1F2|=2c,椭圆的长轴长为2a,
变式训练2(变条件,变设问)若将本例中“PF2⊥F1F2,∠PF1F2=30°”改为“椭圆C上存在点P,使∠F1PF2为钝角”,求椭圆C的离心率的取值范围.
1.椭圆6x2+y2=6的长轴的端点坐标是( )
A.(-1,0),(1,0)
B.(0,-1),(0,1)
答案:D
答案:A
答案:A
