2021年暑假八年级数学北师大版上册 《1.1探索勾股定理》自学专题提升训练(word版含解析)
文档属性
| 名称 | 2021年暑假八年级数学北师大版上册 《1.1探索勾股定理》自学专题提升训练(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 189.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 00:00:00 | ||
图片预览



文档简介
2021年北师大版八年级数学上册《1.1探索勾股定理》暑假自学专题提升训练(附答案)
1.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是( )
A.∠A+∠B=∠C B.a:b:c=3:4:6
C.a2=c2﹣b2 D.∠A:∠B:∠C=1:2:3
2.下列说法错误的是( )
A.△ABC中,若有∠A+∠B=∠C,则△ABC是直角三角形
B.△ABC中,若有∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
C.△ABC的三边长分别为:a,b,c,且a2﹣b2=c2,则△ABC是直角三角形
D.在一个直角三角形中,有两边的长度分别是3和5,则第三边的长度是4
3.下列四组线段中,不能构成直角三角形的是( )
A.3,4,5 B.2,3,4 C. D.13,12,5
4.由下列条件不能判定为直角三角形的是( )
A.∠A+∠B=∠C B.c2﹣a2=b2
C.a=3,b=4,c=5 D.∠A:∠B:∠C=1:1:4
5.有下列判断:①△ABC中,如果a2+b2≠c2,那么△ABC不是直角三角形
②△ABC中,如果a2﹣b2=c2,那么△ABC是直角三角形
③如果△ABC是直角三角形,那么a2+b2=c2其中说法正确的是( )
A.①② B.②③ C.①③ D.②
6.已知a、b、c为△ABC的三边,且满足(a﹣b)(a2+b2﹣c2)=0,则△ABC是( )
A.等边三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
7.在学习“勾股数”的知识时,爱动脑的小明发现了一组有规律的勾股数,并将它们记录在如下的表格中.则当a=24时,b+c的值为( )
a 6 8 10 12 14 …
b 8 15 24 35 48 …
c 10 17 26 37 50 …
A.250 B.288 C.300 D.574
8.下列各组数中,是勾股数的是( )
A.12,15,18 B.12,35,36 C.2,3,4 D.5,12,13
9.下列4组数中能构成直角三角形的是( )
A.5,24,25 B.0.3,0.4,0.5
C.32,42,52 D.8,12,13
10.探索勾股数的规律:观察下列各组数:(3,4,5),(5,12,13),(7,24,25),(9,40,41)…请写出下一数组: .
11.王老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 ……
a 22﹣1 32﹣1 42﹣1 52﹣1 ……
b 4 6 8 10 ……
c 22+1 32+1 42+1 52+1 ……
(1)观察a、b、c与n之间关系,用含自然数n的代数式表示:a= ,b= ,c= .
(2)猜想以a、b、c为边的三角形是否为直角三角形?并证明你的猜想?
(3)观察下列勾股数:32+42=52,52+122=132,72+242=252,92+402=412,分析其中的规律,根据规律写出第五组勾股数.
12.与直角三角形三条边长对应的3个正整数(a,b,c),称为勾股数,《周髀算经》中记载的“勾三股四弦五”中的“3,4,5”就是一组最简单的勾股数,显然,这组数的整数倍,如(6,8,10)(9,12,15)(12,16,20)等都是勾股数.
当然,勾股数远远不止这些,如(5,12,13)(8,15,17)等也都是勾股数.
怎样探索勾股数呢?即怎样一组正整数(a,b,c)才能满足关系式a2+b2=c2
活动1:设(a,b,c)为一组勾股数,如下表:
表1 表2
a b c
a b c
3 4 5
6 8 10
5 12 13
8 15 17
7 24 25
10 24 26
9 40 41
12 35 37
活动2:
(1)观察表1,b、c与a2之间的关系是 ;
(2)根据表1的规律写出勾股数(11, , )
活动3:
(1)观察表2,b、c与a2之间的关系是 ;
(2)根据表2的规律写出勾股数(16, , )
活动4:
一位数学家在他找到的勾股数的表达式中,用2n2+2n+1(n为任意正整数)表示勾股数中的最大的一个数,则另两个数的表达式是 、 (认真观察表1、表2后直接写出结果)
13.如图,每个小正方形的边长都是1,△ABC的三个顶点分别在正方形网格的格点上.
(1)求AB,BC的长;
(2)判断△ABC的形状,并说明理由.
14.如图:在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
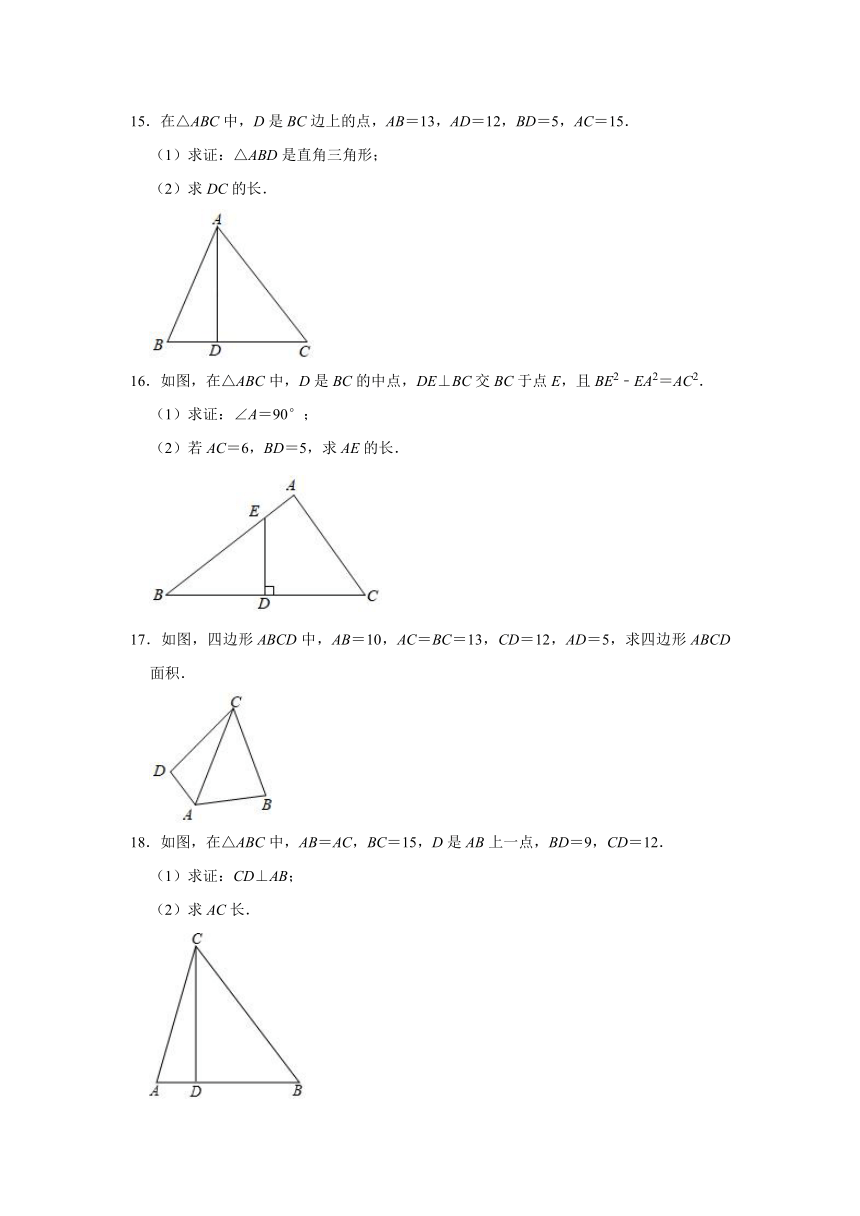
15.在△ABC中,D是BC边上的点,AB=13,AD=12,BD=5,AC=15.
(1)求证:△ABD是直角三角形;
(2)求DC的长.
16.如图,在△ABC中,D是BC的中点,DE⊥BC交BC于点E,且BE2﹣EA2=AC2.
(1)求证:∠A=90°;
(2)若AC=6,BD=5,求AE的长.
17.如图,四边形ABCD中,AB=10,AC=BC=13,CD=12,AD=5,求四边形ABCD面积.
18.如图,在△ABC中,AB=AC,BC=15,D是AB上一点,BD=9,CD=12.
(1)求证:CD⊥AB;
(2)求AC长.
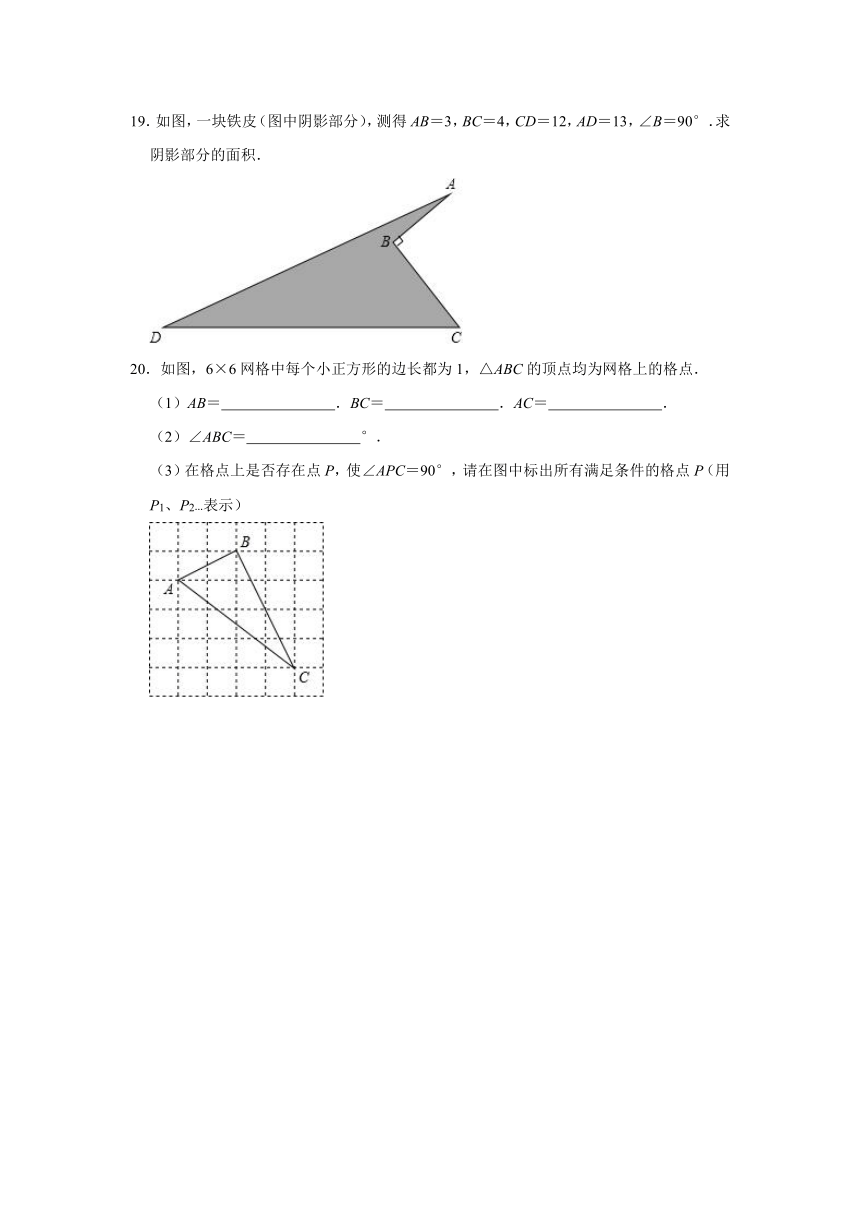
19.如图,一块铁皮(图中阴影部分),测得AB=3,BC=4,CD=12,AD=13,∠B=90°.求阴影部分的面积.
20.如图,6×6网格中每个小正方形的边长都为1,△ABC的顶点均为网格上的格点.
(1)AB= .BC= .AC= .
(2)∠ABC= °.
(3)在格点上是否存在点P,使∠APC=90°,请在图中标出所有满足条件的格点P(用P1、P2…表示)
参考答案
1.解:A、∠A+∠B=∠C,∠C=90°,是直角三角形,不符合题意;
B、∵设a=3x,b=4x,c=6x,(3x)2+(4x)2≠(6x)2,不是直角三角形,符合题意;
C、a2=c2﹣b2,a2+b2=c2,是直角三角形,不符合题意;
D、∵∠A:∠B:∠C=1:2:3,∴∠C=90°,是直角三角形,不符合题意;
故选:B.
2.解:A、△ABC中,若有∠A+∠B=∠C,则∠C=90°,∴△ABC是直角三角形,说法正确;
B、△ABC中,若有∠A:∠B:∠C=1:2:3,则∠C=90°,∴△ABC是直角三角形,说法正确;
C、△ABC的三边长分别为:a,b,c,且a2﹣b2=c2,则a2=b2+c2,∴△ABC是直角三角形,说法正确;
D、在一个直角三角形中,有两边的长度分别是3和5,则第三边的长度是4或,说法错误;
故选:D.
3.解:A、32+42=52,能构成直角三角形,故此选项不合题意;
B、22+32≠42,不能构成直角三角形,故此选项符合题意;
C、12+()2=()2,能构成直角三角形,故此选项不合题意;
D、52+122=132,能构成直角三角形,故此选项不合题意;
故选:B.
4.解:A、∵∠A+∠B=∠C,
∴∠A+∠B+∠C=2∠C=180°,
∴最大的角∠C=90°,是直角三角形,故本选项不符合题意;
B、c2﹣a2=b2,即a2+b2=c2,故是直角三角形,故本选项不符合题意;
C、∵32+42=52,故是直角三角形,故本选项不符合题意;
D、∵∠A:∠B:∠C=1:1:4,∴∠C=,故不能判定是直角三角形,故选项符合题意;
故选:D.
5.解:①a=3,b=5,c=4,32+52≠42,32+42=52则△ABC可能是直角三角形,故原来说法错误;
②△ABC中,如果a2﹣b2=c2,那么△ABC是直角三角形,说法正确;
③如果△ABC是直角三角形,a=3,b=5,c=4,那么a2+c2=b2,但是a2+b2≠c2,故原来说法错误.
∴其中说法正确的只有②,
故选:D.
6.解:∵(a﹣b)(a2+b2﹣c2)=0,
∴a﹣b=0,或a2+b2﹣c2=0,
即a=b或a2+b2=c2,
∴△ABC的形状为等腰三角形或直角三角形.
故选:D.
7.解:从表中可知:a依次为6,8,10,12,14,16,18,20,22,24,???,即24=2×(10+2),
b依次为8,15,24,35,48,???,即当a=24时,b=122﹣1=143,
c依次为10,17,26,37,50,???,即当a=24时,c=122+1=145,
所以当a=24时,b+c=143+145=288,
故选:B.
8.解:A、122+152≠182,不是勾股数,故此选项不合题意;
B、122+352≠362,不是勾股数,故此选项不合题意;
C、22+32≠42,不是勾股数,故此选项不合题意;
D、52+122=132,都是正整数,是勾股数,故此选项符合题意;
故选:D.
9.解:A、∵52+242≠252,∴以这三个数为长度的线段不能构成直角三角形,故此选项错误;
B、∵0.32+0.42=0.52,∴以这三个数为长度的线段能构成直角三角形,故此选项正确;
C、∵92+162≠252,∴以这三个数为长度的线段不能构成直角三角形,故此选项错误;
D、∵82+122≠132,∴以这三个数为长度的线段不能构成直角三角形,故此选项错误.
故选:B.
10.解:∵(3,4,5):3=2×1+1,4=2×12+2×1,5=2×12+2×1+1;
(5,12,13):5=2×2+1,12=2×22+2×2,13=2×22+2×2+1;
(7,24,25):7=2×3+1,24=2×32+2×3,25=2×32+2×3+1;
(9,40,41):9=2×4+1,40=2×42+2×4,41=2×42+2×4+1;
∴下一组数为:11=2×5+1,60=2×52+2×5,61=2×52+2×5+1,
故答案为:(11,60,61).
11.解:(1)由题意:a=n2﹣1,b=2n,c=n2+1,
故答案为:n2﹣1,2n,n2+1;
(2)猜想:以a、b、c为边的三角形是直角三角形.
理由:∵a=n2﹣1,b=2n,c=n2+1,
∴a2+b2=(n2﹣1)2+4n2=n4+2n2+1=(n2+1)2=c2,
∴以a、b、c为边的三角形是直角三角形.
(3)观察可知:第五组勾股数为:112+602=612.
12.解:活动2:
(1)b、c与a2之间的关系是a2=b+c;
(2)∵a2=b+c,a=11,
∴b+c=121,
∵b=c﹣1,
∴b=60,c=61;
活动3:(1)b、c与a2之间的关系是a2=b+c;
(2)∵a2=b+c,a=16,
∴b+c=128,
∵b=c﹣2,
∴b=63,c=65;
活动4:已知c=2n2+2n+1,
如果满足表1的规律,那么b=c﹣1,a2=b+c,
∴b=2n2+2n,a2=4n2+4n+1,
∴a=2n+1,符合题意;
如果满足表2的规律,那么b=c﹣2,a2=b+c,
∴b=2n2+2n﹣1,a2=4n2+4n,
∴a2=8n2+8n,不是完全平方数,不符合题意;
综上所述,另两个数的表达式是2n2+2n,2n+1.
故答案为a2=b+c;60,61;a2=b+c;63,65;2n2+2n,2n+1.
13.解:(1)AB=,BC=,
(2)AC=5,
∵,
∴AB2+BC2=AC2,
∴△ABC是直角三角形.
14.解:∵∠B=90°,
∴△ABC为直角三角形,
又∵AB=3,BC=4,
∴根据勾股定理得:AC==5,
又∵CD=12,AD=13,
∴AD2=132=169,CD2+AC2=122+52=144+25=169,
∴CD2+AC2=AD2,
∴△ACD为直角三角形,∠ACD=90°,
则S四边形ABCD=S△ABC+S△ACD=AB?BC+AC?CD=×3×4+×5×12=36.
故四边形ABCD的面积是36.
15.(1)证明:∵AB=13,AD=12,BD=5,
∴AB2=AD2+BD2,
∴△ABD是直角三角形,即∠ADB=90°;
(2)解:∵∠ADB=90°,
∴△ADC是直角三角形,
在Rt△ADC中,DC==9.
16.(1)证明:连接CE,如图,
∵D是BC的中点,DE⊥BC,
∴CE=BE,
∵BE2﹣EA2=AC2,
∴CE2﹣EA2=AC2,
∴EA2+AC2=CE2,
∴△ACE是直角三角形,即∠A=90°;
(2)解:∵D是BC的中点,BD=5,
∴BC=2BD=10,
∵∠A=90°,AC=6,
∴AB===8,
在Rt△AEC中,EA2+AC2=CE2,
∵CE=BE,
∴62+AE2=(8﹣AE)2,
解得:x=,
∴AE的长为.
17.解:过点C作CE⊥AB于点E.
∵AC=13,CD=12,AD=5,132=122+52,
∴AC2=CD2+AD2,
∴△ACD是直角三角形,
∵AC=BC=13,AB=10,CE⊥AB,
∴AE=BE=AB=×10=5.
在Rt△CAE中,
CE===12.
∴S四边形ABCD=S△DAC+S△ABC=×5×12+×10×12=30+60=90.
即四边形ABCD面积为90.
18.(1)证明:∵BC=15,BD=9,CD=12,
∴BD2+CD2=92+122=152=BC2,
∴∠CDB=90°,
∴CD⊥AB;
(2)解:∵AB=AC,
∴AC=AB=AD+BD=AD+9,
∵∠ADC=90°,
∴AC2=AD2+CD2,
∴(AD+9)2=AD2+122,
∴AD=,
∴AC=+9=.
19.解:如图,连接AC.
∵△ABC中,∠B=90°,AB=3,BC=4,
∴AC==5.
∵CD=12,AD=13,AC=5,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,
∴S阴影=S△ACD﹣S△ABC=×5×12﹣×3×4=30﹣6=24.
20.解:(1)AB==.BC==2.AC==5.
(2)∵()2+(2)2=52,
∴∠ABC=90°.
(3)如图所示:
1.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是( )
A.∠A+∠B=∠C B.a:b:c=3:4:6
C.a2=c2﹣b2 D.∠A:∠B:∠C=1:2:3
2.下列说法错误的是( )
A.△ABC中,若有∠A+∠B=∠C,则△ABC是直角三角形
B.△ABC中,若有∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
C.△ABC的三边长分别为:a,b,c,且a2﹣b2=c2,则△ABC是直角三角形
D.在一个直角三角形中,有两边的长度分别是3和5,则第三边的长度是4
3.下列四组线段中,不能构成直角三角形的是( )
A.3,4,5 B.2,3,4 C. D.13,12,5
4.由下列条件不能判定为直角三角形的是( )
A.∠A+∠B=∠C B.c2﹣a2=b2
C.a=3,b=4,c=5 D.∠A:∠B:∠C=1:1:4
5.有下列判断:①△ABC中,如果a2+b2≠c2,那么△ABC不是直角三角形
②△ABC中,如果a2﹣b2=c2,那么△ABC是直角三角形
③如果△ABC是直角三角形,那么a2+b2=c2其中说法正确的是( )
A.①② B.②③ C.①③ D.②
6.已知a、b、c为△ABC的三边,且满足(a﹣b)(a2+b2﹣c2)=0,则△ABC是( )
A.等边三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
7.在学习“勾股数”的知识时,爱动脑的小明发现了一组有规律的勾股数,并将它们记录在如下的表格中.则当a=24时,b+c的值为( )
a 6 8 10 12 14 …
b 8 15 24 35 48 …
c 10 17 26 37 50 …
A.250 B.288 C.300 D.574
8.下列各组数中,是勾股数的是( )
A.12,15,18 B.12,35,36 C.2,3,4 D.5,12,13
9.下列4组数中能构成直角三角形的是( )
A.5,24,25 B.0.3,0.4,0.5
C.32,42,52 D.8,12,13
10.探索勾股数的规律:观察下列各组数:(3,4,5),(5,12,13),(7,24,25),(9,40,41)…请写出下一数组: .
11.王老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 ……
a 22﹣1 32﹣1 42﹣1 52﹣1 ……
b 4 6 8 10 ……
c 22+1 32+1 42+1 52+1 ……
(1)观察a、b、c与n之间关系,用含自然数n的代数式表示:a= ,b= ,c= .
(2)猜想以a、b、c为边的三角形是否为直角三角形?并证明你的猜想?
(3)观察下列勾股数:32+42=52,52+122=132,72+242=252,92+402=412,分析其中的规律,根据规律写出第五组勾股数.
12.与直角三角形三条边长对应的3个正整数(a,b,c),称为勾股数,《周髀算经》中记载的“勾三股四弦五”中的“3,4,5”就是一组最简单的勾股数,显然,这组数的整数倍,如(6,8,10)(9,12,15)(12,16,20)等都是勾股数.
当然,勾股数远远不止这些,如(5,12,13)(8,15,17)等也都是勾股数.
怎样探索勾股数呢?即怎样一组正整数(a,b,c)才能满足关系式a2+b2=c2
活动1:设(a,b,c)为一组勾股数,如下表:
表1 表2
a b c
a b c
3 4 5
6 8 10
5 12 13
8 15 17
7 24 25
10 24 26
9 40 41
12 35 37
活动2:
(1)观察表1,b、c与a2之间的关系是 ;
(2)根据表1的规律写出勾股数(11, , )
活动3:
(1)观察表2,b、c与a2之间的关系是 ;
(2)根据表2的规律写出勾股数(16, , )
活动4:
一位数学家在他找到的勾股数的表达式中,用2n2+2n+1(n为任意正整数)表示勾股数中的最大的一个数,则另两个数的表达式是 、 (认真观察表1、表2后直接写出结果)
13.如图,每个小正方形的边长都是1,△ABC的三个顶点分别在正方形网格的格点上.
(1)求AB,BC的长;
(2)判断△ABC的形状,并说明理由.
14.如图:在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
15.在△ABC中,D是BC边上的点,AB=13,AD=12,BD=5,AC=15.
(1)求证:△ABD是直角三角形;
(2)求DC的长.
16.如图,在△ABC中,D是BC的中点,DE⊥BC交BC于点E,且BE2﹣EA2=AC2.
(1)求证:∠A=90°;
(2)若AC=6,BD=5,求AE的长.
17.如图,四边形ABCD中,AB=10,AC=BC=13,CD=12,AD=5,求四边形ABCD面积.
18.如图,在△ABC中,AB=AC,BC=15,D是AB上一点,BD=9,CD=12.
(1)求证:CD⊥AB;
(2)求AC长.
19.如图,一块铁皮(图中阴影部分),测得AB=3,BC=4,CD=12,AD=13,∠B=90°.求阴影部分的面积.
20.如图,6×6网格中每个小正方形的边长都为1,△ABC的顶点均为网格上的格点.
(1)AB= .BC= .AC= .
(2)∠ABC= °.
(3)在格点上是否存在点P,使∠APC=90°,请在图中标出所有满足条件的格点P(用P1、P2…表示)
参考答案
1.解:A、∠A+∠B=∠C,∠C=90°,是直角三角形,不符合题意;
B、∵设a=3x,b=4x,c=6x,(3x)2+(4x)2≠(6x)2,不是直角三角形,符合题意;
C、a2=c2﹣b2,a2+b2=c2,是直角三角形,不符合题意;
D、∵∠A:∠B:∠C=1:2:3,∴∠C=90°,是直角三角形,不符合题意;
故选:B.
2.解:A、△ABC中,若有∠A+∠B=∠C,则∠C=90°,∴△ABC是直角三角形,说法正确;
B、△ABC中,若有∠A:∠B:∠C=1:2:3,则∠C=90°,∴△ABC是直角三角形,说法正确;
C、△ABC的三边长分别为:a,b,c,且a2﹣b2=c2,则a2=b2+c2,∴△ABC是直角三角形,说法正确;
D、在一个直角三角形中,有两边的长度分别是3和5,则第三边的长度是4或,说法错误;
故选:D.
3.解:A、32+42=52,能构成直角三角形,故此选项不合题意;
B、22+32≠42,不能构成直角三角形,故此选项符合题意;
C、12+()2=()2,能构成直角三角形,故此选项不合题意;
D、52+122=132,能构成直角三角形,故此选项不合题意;
故选:B.
4.解:A、∵∠A+∠B=∠C,
∴∠A+∠B+∠C=2∠C=180°,
∴最大的角∠C=90°,是直角三角形,故本选项不符合题意;
B、c2﹣a2=b2,即a2+b2=c2,故是直角三角形,故本选项不符合题意;
C、∵32+42=52,故是直角三角形,故本选项不符合题意;
D、∵∠A:∠B:∠C=1:1:4,∴∠C=,故不能判定是直角三角形,故选项符合题意;
故选:D.
5.解:①a=3,b=5,c=4,32+52≠42,32+42=52则△ABC可能是直角三角形,故原来说法错误;
②△ABC中,如果a2﹣b2=c2,那么△ABC是直角三角形,说法正确;
③如果△ABC是直角三角形,a=3,b=5,c=4,那么a2+c2=b2,但是a2+b2≠c2,故原来说法错误.
∴其中说法正确的只有②,
故选:D.
6.解:∵(a﹣b)(a2+b2﹣c2)=0,
∴a﹣b=0,或a2+b2﹣c2=0,
即a=b或a2+b2=c2,
∴△ABC的形状为等腰三角形或直角三角形.
故选:D.
7.解:从表中可知:a依次为6,8,10,12,14,16,18,20,22,24,???,即24=2×(10+2),
b依次为8,15,24,35,48,???,即当a=24时,b=122﹣1=143,
c依次为10,17,26,37,50,???,即当a=24时,c=122+1=145,
所以当a=24时,b+c=143+145=288,
故选:B.
8.解:A、122+152≠182,不是勾股数,故此选项不合题意;
B、122+352≠362,不是勾股数,故此选项不合题意;
C、22+32≠42,不是勾股数,故此选项不合题意;
D、52+122=132,都是正整数,是勾股数,故此选项符合题意;
故选:D.
9.解:A、∵52+242≠252,∴以这三个数为长度的线段不能构成直角三角形,故此选项错误;
B、∵0.32+0.42=0.52,∴以这三个数为长度的线段能构成直角三角形,故此选项正确;
C、∵92+162≠252,∴以这三个数为长度的线段不能构成直角三角形,故此选项错误;
D、∵82+122≠132,∴以这三个数为长度的线段不能构成直角三角形,故此选项错误.
故选:B.
10.解:∵(3,4,5):3=2×1+1,4=2×12+2×1,5=2×12+2×1+1;
(5,12,13):5=2×2+1,12=2×22+2×2,13=2×22+2×2+1;
(7,24,25):7=2×3+1,24=2×32+2×3,25=2×32+2×3+1;
(9,40,41):9=2×4+1,40=2×42+2×4,41=2×42+2×4+1;
∴下一组数为:11=2×5+1,60=2×52+2×5,61=2×52+2×5+1,
故答案为:(11,60,61).
11.解:(1)由题意:a=n2﹣1,b=2n,c=n2+1,
故答案为:n2﹣1,2n,n2+1;
(2)猜想:以a、b、c为边的三角形是直角三角形.
理由:∵a=n2﹣1,b=2n,c=n2+1,
∴a2+b2=(n2﹣1)2+4n2=n4+2n2+1=(n2+1)2=c2,
∴以a、b、c为边的三角形是直角三角形.
(3)观察可知:第五组勾股数为:112+602=612.
12.解:活动2:
(1)b、c与a2之间的关系是a2=b+c;
(2)∵a2=b+c,a=11,
∴b+c=121,
∵b=c﹣1,
∴b=60,c=61;
活动3:(1)b、c与a2之间的关系是a2=b+c;
(2)∵a2=b+c,a=16,
∴b+c=128,
∵b=c﹣2,
∴b=63,c=65;
活动4:已知c=2n2+2n+1,
如果满足表1的规律,那么b=c﹣1,a2=b+c,
∴b=2n2+2n,a2=4n2+4n+1,
∴a=2n+1,符合题意;
如果满足表2的规律,那么b=c﹣2,a2=b+c,
∴b=2n2+2n﹣1,a2=4n2+4n,
∴a2=8n2+8n,不是完全平方数,不符合题意;
综上所述,另两个数的表达式是2n2+2n,2n+1.
故答案为a2=b+c;60,61;a2=b+c;63,65;2n2+2n,2n+1.
13.解:(1)AB=,BC=,
(2)AC=5,
∵,
∴AB2+BC2=AC2,
∴△ABC是直角三角形.
14.解:∵∠B=90°,
∴△ABC为直角三角形,
又∵AB=3,BC=4,
∴根据勾股定理得:AC==5,
又∵CD=12,AD=13,
∴AD2=132=169,CD2+AC2=122+52=144+25=169,
∴CD2+AC2=AD2,
∴△ACD为直角三角形,∠ACD=90°,
则S四边形ABCD=S△ABC+S△ACD=AB?BC+AC?CD=×3×4+×5×12=36.
故四边形ABCD的面积是36.
15.(1)证明:∵AB=13,AD=12,BD=5,
∴AB2=AD2+BD2,
∴△ABD是直角三角形,即∠ADB=90°;
(2)解:∵∠ADB=90°,
∴△ADC是直角三角形,
在Rt△ADC中,DC==9.
16.(1)证明:连接CE,如图,
∵D是BC的中点,DE⊥BC,
∴CE=BE,
∵BE2﹣EA2=AC2,
∴CE2﹣EA2=AC2,
∴EA2+AC2=CE2,
∴△ACE是直角三角形,即∠A=90°;
(2)解:∵D是BC的中点,BD=5,
∴BC=2BD=10,
∵∠A=90°,AC=6,
∴AB===8,
在Rt△AEC中,EA2+AC2=CE2,
∵CE=BE,
∴62+AE2=(8﹣AE)2,
解得:x=,
∴AE的长为.
17.解:过点C作CE⊥AB于点E.
∵AC=13,CD=12,AD=5,132=122+52,
∴AC2=CD2+AD2,
∴△ACD是直角三角形,
∵AC=BC=13,AB=10,CE⊥AB,
∴AE=BE=AB=×10=5.
在Rt△CAE中,
CE===12.
∴S四边形ABCD=S△DAC+S△ABC=×5×12+×10×12=30+60=90.
即四边形ABCD面积为90.
18.(1)证明:∵BC=15,BD=9,CD=12,
∴BD2+CD2=92+122=152=BC2,
∴∠CDB=90°,
∴CD⊥AB;
(2)解:∵AB=AC,
∴AC=AB=AD+BD=AD+9,
∵∠ADC=90°,
∴AC2=AD2+CD2,
∴(AD+9)2=AD2+122,
∴AD=,
∴AC=+9=.
19.解:如图,连接AC.
∵△ABC中,∠B=90°,AB=3,BC=4,
∴AC==5.
∵CD=12,AD=13,AC=5,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,
∴S阴影=S△ACD﹣S△ABC=×5×12﹣×3×4=30﹣6=24.
20.解:(1)AB==.BC==2.AC==5.
(2)∵()2+(2)2=52,
∴∠ABC=90°.
(3)如图所示:
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
