广东地区专用2021-2022学年八年级数学北师大版上册 第三章位置与坐标 单元检测卷(word版含答案解析)
文档属性
| 名称 | 广东地区专用2021-2022学年八年级数学北师大版上册 第三章位置与坐标 单元检测卷(word版含答案解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 398.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 00:00:00 | ||
图片预览


文档简介
单元检测卷-2021-2022学年八年级数学北师大版上册 (广东地区专用)
第三章位置与坐标
一、单选题(在下列各题的四个选项中,只有一项是符合题意的.本题共10个小题)
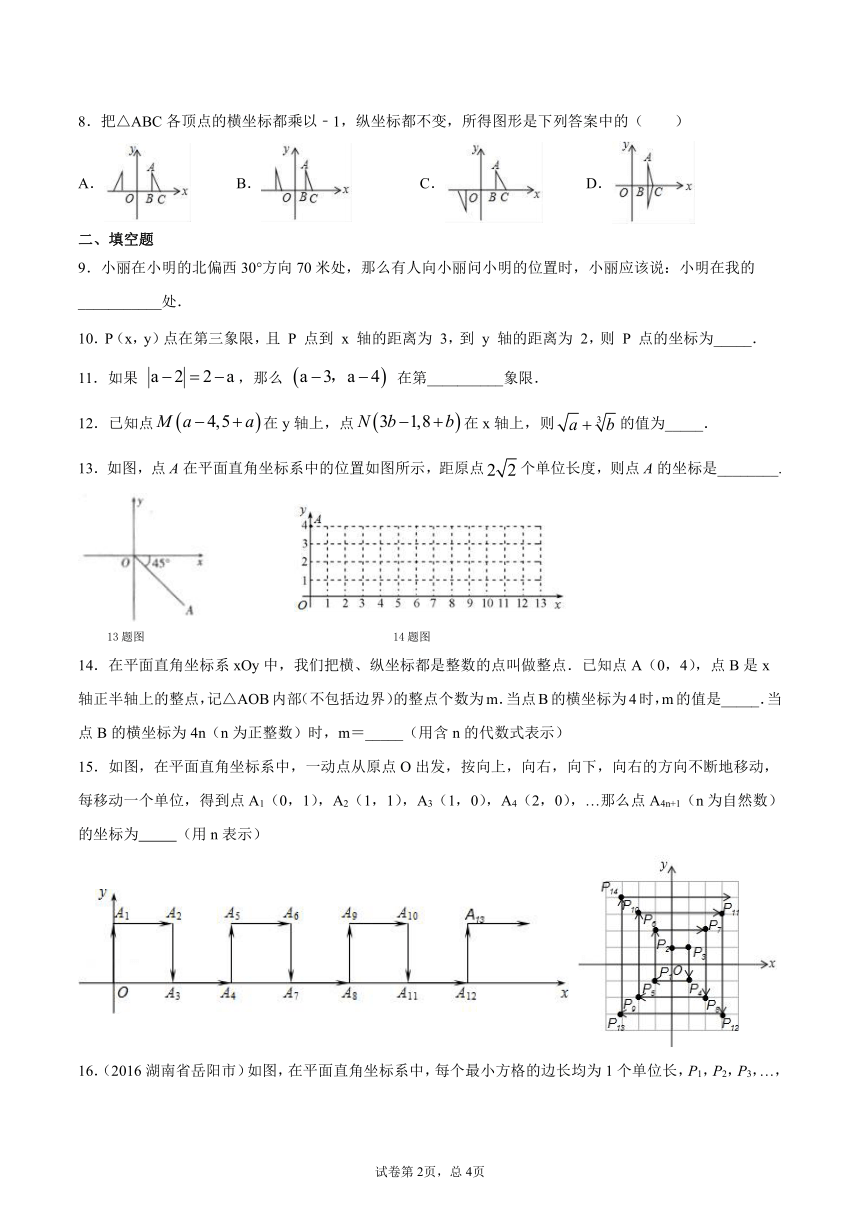
1.某次大型活动由大学生组成仪仗队,若同学甲站在第六行第八列,可以表示为(6,8),则乙同学站第20行第7列,表示为( )
A.(7,20) B.(20,7) C.(7,7) D.(20,20)
2.如图所示,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,小明走下面( )线路不能到达学校.
473265572390A.(0,4)→(0,0)→(4,0)
B.(0,4)→(4,4)→(4,0)
C.(0,4)→(1,4)→(1,1)→(4,1)→(4,0)
D.(0,4)→(3,4)→(4,2)→(4,0)
3.点false关于false轴对称的点false的坐标是( )
A.false B.false C.false D.false
4.如图,小手盖住的点的坐标可能为( )
A.(5,2) B.(-6,3) C.(-4,-6) D.(3,-4)
4题图 7题图
5.若点false满足false,则点M所在象限是( )
A.第一、三象限 B.第二、四象限 C.第一、二象限 D.不能确定
6.已知点A(4,2),B(-2,2),则直线AB ( )
A.平行于x轴 B.平行于y轴 C.经过原点 D.以上都有可能
7.如图,一艘海轮位于灯塔P的南偏东70°方向的M处, 它以每小时40海里的速度向正北方向航行,2小时后到 达位于灯塔P的北偏东40°的N处,则N处与灯塔P的 距离为
A.40海里 B.60海里 C.70海里 D.80海里
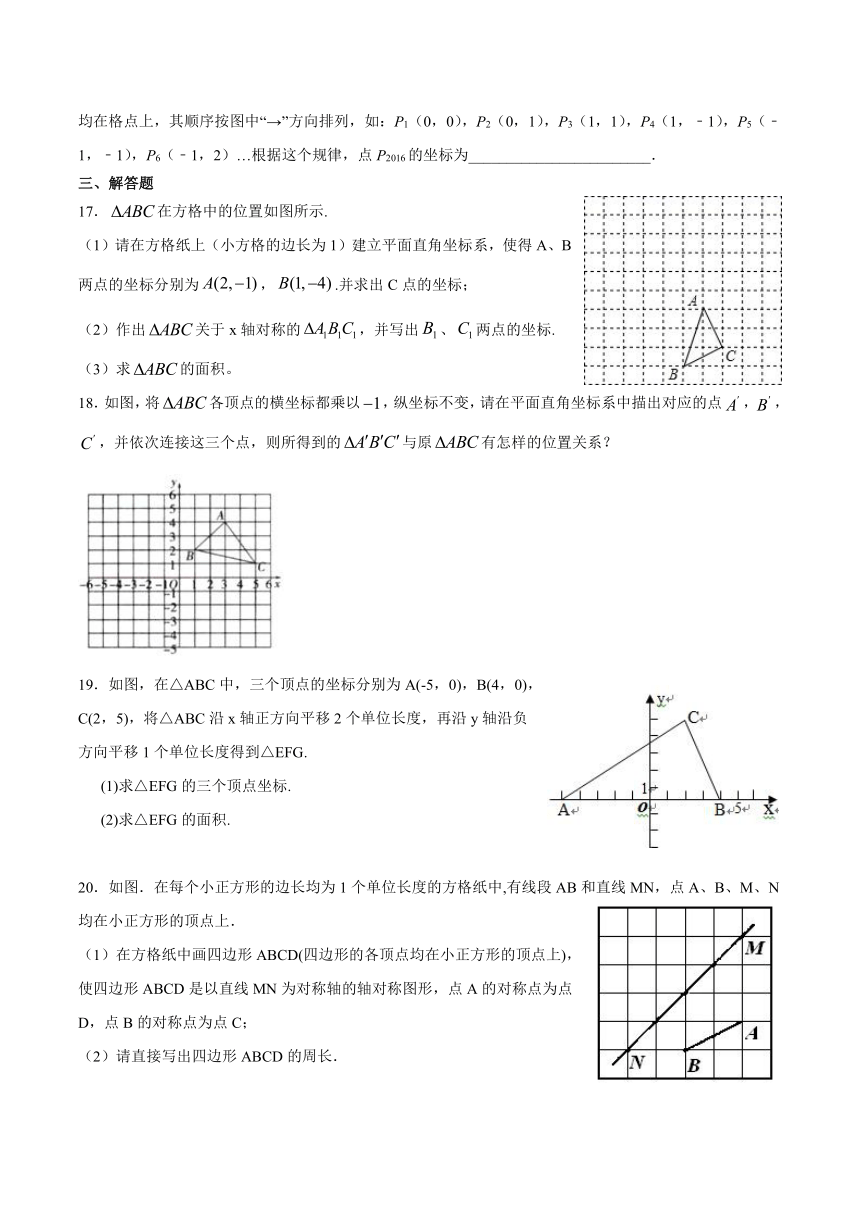
8.把△ABC各顶点的横坐标都乘以﹣1,纵坐标都不变,所得图形是下列答案中的( )
A. B. C. D.
二、填空题
9.小丽在小明的北偏西30°方向70米处,那么有人向小丽问小明的位置时,小丽应该说:小明在我的___________处.
10.P(x,y)点在第三象限,且 P 点到 x 轴的距离为 3,到 y 轴的距离为 2,则 P 点的坐标为_____.
11.如果 false,那么 false 在第__________象限.
12.已知点false在y轴上,点false在x轴上,则false的值为_____.
13.如图,点A在平面直角坐标系中的位置如图所示,距原点false个单位长度,则点A的坐标是________.
13题图 14题图
14.在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当点B的横坐标为4时,m的值是_____.当点B的横坐标为4n(n为正整数)时,m=_____(用含n的代数式表示)
15.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (用n表示)
16.(2016湖南省岳阳市)如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长,P1,P2,P3,…,均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,﹣1),P5(﹣1,﹣1),P6(﹣1,2)…根据这个规律,点P2016的坐标为________________________.
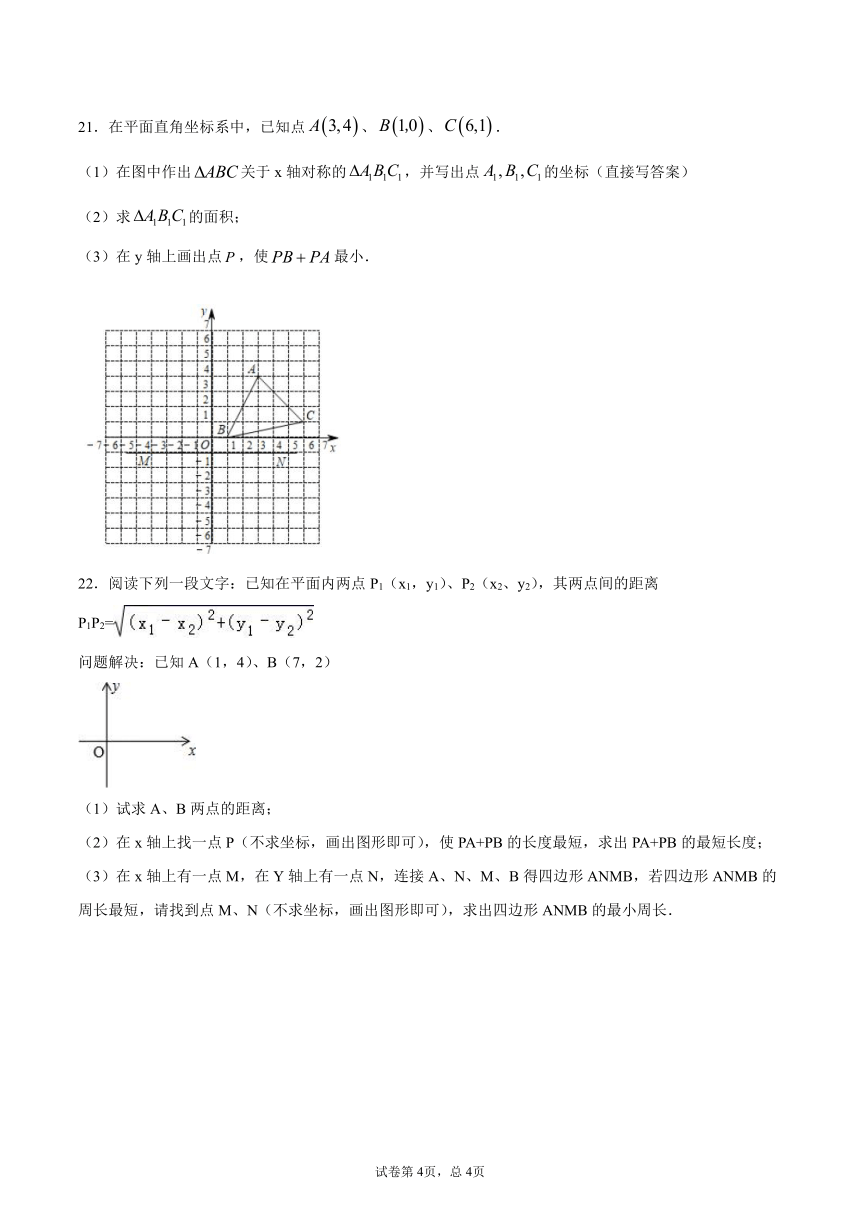
三、解答题
44538901968517.false在方格中的位置如图所示.
(1)请在方格纸上(小方格的边长为1)建立平面直角坐标系,使得A、B两点的坐标分别为false,false.并求出C点的坐标;
(2)作出false关于x轴对称的false,并写出false、false两点的坐标.
(3)求false的面积。
18.如图,将false各顶点的横坐标都乘以false,纵坐标不变,请在平面直角坐标系中描出对应的点false,false,false,并依次连接这三个点,则所得到的false与原false有怎样的位置关系?
413194515621019.如图,在△ABC中,三个顶点的坐标分别为A(-5,0),B(4,0),C(2,5),将△ABC沿x轴正方向平移2个单位长度,再沿y轴沿负方向平移1个单位长度得到△EFG.
(1)求△EFG的三个顶点坐标.
(2)求△EFG的面积.
449643527178020.如图.在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A、B、M、N均在小正方形的顶点上.
(1)在方格纸中画四边形ABCD(四边形的各顶点均在小正方形的顶点上),使四边形ABCD是以直线MN为对称轴的轴对称图形,点A的对称点为点D,点B的对称点为点C;
(2)请直接写出四边形ABCD的周长.
21.在平面直角坐标系中,已知点false、false、false.
(1)在图中作出false关于x轴对称的false,并写出点false的坐标(直接写答案)
(2)求false的面积;
(3)在y轴上画出点false,使false最小.
22.阅读下列一段文字:已知在平面内两点P1(x1,y1)、P2(x2、y2),其两点间的距离P1P2=
问题解决:已知A(1,4)、B(7,2)
(1)试求A、B两点的距离;
(2)在x轴上找一点P(不求坐标,画出图形即可),使PA+PB的长度最短,求出PA+PB的最短长度;
(3)在x轴上有一点M,在Y轴上有一点N,连接A、N、M、B得四边形ANMB,若四边形ANMB的周长最短,请找到点M、N(不求坐标,画出图形即可),求出四边形ANMB的最小周长.
参考答案
1.B
【详解】
试题分析:根据题意可知行与列的表示为(行数,列数),因此可知第20行第7列表示为(20,7).
故选B
考点:坐标系
2.D
【解析】
【分析】根据题意,在给出的图形中画一下四个选项的行走路线即可得出小明不能到达学校的路线.
【详解】A. (0,4)→(0,0)→(4,0),能到达学校,故不符合题意;
B. (0,4)→(4,4)→(4,0),能到达学校,故不符合题意;
C. (0,4)→(1,4)→(1,1)→(4,1)→(4,0),能到达学校,故不符合题意;
D. (0,4)→(3,4)→(4,2)→(4,0),不能到达学校,故符合题意,
故选D.
【点睛】本题考查了利用坐标确定位置,也考查了数学在生活中的应用,结合题意,自己动手操作一下即可更准确地得到结论.
3.C
【分析】
根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”解答.
【详解】
解:点M(-1,2)关于x轴对称的点的坐标为(-1,-2).
故选:C.
【点睛】
本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数.
4.C
【详解】
根据题意,小手盖住的点在第三象限,结合第三象限点的坐标特点,分析选项可得答案.
解答:解:根据图示,小手盖住的点在第三象限,
第三象限的点坐标特点是:横负纵负;
分析选项可得只有C符合.
故选C.
点评:本题主要考查了点在第三象限时点的坐标特征,比较简单.注意四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
5.B
【分析】
利用完全平方公式展开并整理得到false,从而判断出false、false异号,再根据各象限内点的坐标特征解答.
【详解】
解:false,
false,
false,
false、false异号,
false点false在第二、四象限.
故选:false.
【点睛】
本题考查了完全平方公式,各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键.
6.A
【详解】
A(4,2),B(-2,2)
∴点A到x轴的距离为2,点B到x轴的距离为2
且A、B都在x轴上方
∴AB平行于x轴,故选A.
点睛:此题是研究平面直角坐标系中,两个点所连线段与坐标轴的位置关系,需要对点到直线的距离有着明确地理解,而且此题属于较简单的判断线与坐标轴位置关系的一类问题.
7.D
【详解】
分析:依题意,知MN=40海里/小时×2小时=80海里,
∵根据方向角的意义和平行的性质,∠M=70°,∠N=40°,
∴根据三角形内角和定理得∠MPN=70°.∴∠M=∠MPN=70°.
∴NP=NM=80海里.故选D.
8.A
【分析】
平面直角坐标系中任意一点P(x,y),关于x轴的对称点的坐标是(x,﹣y),关于y轴的对称点的坐标是(﹣x,y),三个顶点坐标的横坐标都乘以﹣1,并保持纵坐标不变,就是横坐标变成相反数.即所得到的点与原来的点关于y轴对称.
【详解】
解:根据轴对称的性质,知将△ABC的三个顶点的横坐标乘以﹣1,就是把横坐标变成相反数,纵坐标不变,
因而是把三角形的三个顶点以y轴为对称轴进行轴对称变换.所得图形与原图形关于y轴对称.
故选A.
【点睛】
本题主要考查了关于y轴对称点的性质,正确应用坐标判断两点关于y轴对称的方法:横坐标互为相反数,纵坐标相同是解题关键.
9.南偏东30°方向70米
【分析】
直接利用方向角的定义分析得出答案.北
【详解】
如图所示:
∵小丽在小明的北偏西30°方向,距离小明70米处,
∴小丽应该说:小明在我的南偏东30°方向70米处.
故答案为:南偏东30°方向 70米.
【点睛】
本题主要考查了用方向角和距离确定物体的位置,正确画出图形是解题关键.
10.(-2,-3)
【分析】
平面直角坐标系中,点到x 轴的距离为是这个点纵坐标的绝对值, 点到y 轴的距离为是这个点横坐标的绝对值,由此解题即可.
【详解】
∵P(x,y)点在第三象限,且 P 点到 x 轴的距离为 3,到 y 轴的距离为 2,
∴由平面直角坐标系各象限点的特征可知,P(-2,-3).
【点睛】
本题考查了平面直角坐标系中,点的特征,属于简单题,理解清楚点的横纵坐标的几何意义是解题关键.
11.三
【分析】
根据绝对值的性质可得false,解得false,再根据各象限内点的坐标特征解答.
【详解】
解:false,
false,
解得false,
false,false,
false在第三象限.
故答案为:三.
【点睛】
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限false;第二象限false;第三象限false;第四象限false.
12.0
【分析】
根据x轴、y轴上的点的坐标特点可得false,false,即可求出a、b的值,代入即可得答案.
【详解】
∵点false在y轴上,点false在x轴上,
∴false,false,
∴false,false,
∴false.
【点睛】
本题考查坐标系中,x轴、y轴上的点的坐标特点,x轴上的点的纵坐标都为0;y轴上的点的横坐标都为0.
13.false
【分析】
过A作AB⊥x轴于点B,由勾股定理可得AB=OB=2,由勾股定理可得AB=OB=2,进一步可得点A的坐标.
【详解】
解:过A作AB⊥x轴于点B,
∵∠AOB=45°,
∴AB=OB,AO=false
由勾股定理可得AB=OB=2
又∵A在第四象限
∴点A的坐标为(2,-2)
故答案为(2,-2)
【点睛】
本题考查了点的坐标,解题关键是作出图形应用勾股定理求出点到坐标轴的距离.
14.3, 6n﹣3
【分析】
根据题意,分别找出n=1、2、3时的整点的个数,即可发现n增加1,整点的个数增加6,然后写出横坐标为4n时的表达式即可.
【详解】
解:如图,n=1,即点B的横坐标为4时,整点个数为:6×1﹣3=3,
n=2,即点B的横坐标为8时,整点个数为:6×2﹣3=9,
n=3,即点B的横坐标为12时,整点个数为:6×3﹣3=15,
n=4,即点B的横坐标为16时,整点个数为:6×4﹣3=21,
…,
所以,点B的横坐标为4n时,整点个数为6n﹣3.
故答案为3,6n﹣3.
【点睛】
此题主要考查了点的坐标规律,根据图形找出整点个数的变化规律:n增加1,整点的个数增加6是解题的关键.
15.(2n,1)
【详解】
试题分析:根据图形分别求出n=1、2、3时对应的点A4n+1的坐标,然后根据变化规律写出即可:
由图可知,n=1时,4×1+1=5,点A5(2,1),
n=2时,4×2+1=9,点A9(4,1),
n=3时,4×3+1=13,点A13(6,1),
∴点A4n+1(2n,1).
16.(504,﹣504)
【详解】
根据各个点的位置关系,可得出下标为4的倍数的点在第四象限的角平分线上,被4除余1的点在第三象限的角平分线上,被4除余2的点在第二象限的角平分线上,被4除余3的点在第一象限的角平分线上,点P2016在第四象限的角平分线上,且横纵坐标的绝对值=2016÷4,
由规律可得,2016÷4=504,∴点P2016的在第四象限的角平分线上,
∵点P4(1,﹣1),点P8(2,﹣2),点P12(3,﹣3),
∴点P2016(504,﹣504),
故答案为(504,﹣504).
17.(1)画图见解析,false;(2)画图见解析,Bfalse;(3)2.5
【分析】
(1)根据点A的坐标可知坐标原点在点A左边两个单位,上边一个单位,再求出C的坐标即可;
(2)找到与x轴对称的且到x轴的距离为1的A1,同法做其他点的对应点即可得到△ABC关于x轴对称的△A1B1C1.
(3)利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积进行计算求解.
【详解】
(1)建立的平面直角坐标系如下所示:
其中C点的坐标为:C(3,-3);
(2)所作图形如上所示,其中B1,C1的坐标分别为:(1,4),(3,3);
(3)S△ABC=2×3-false×1×3-false×2×1-false×2×1
=6-3.5
=2.5.
【点睛】
本题考查轴对称作图,掌握画图的方法和图形的特点是关键;会根据一个点的坐标得到坐标原点.(3)中求三角形的面积通常都是利用三角形所在的矩形的面积减去四周三角形的面积求解,此方法需要掌握.
18.与原图形关于y轴对称
【分析】
利用△ABC各顶点的横坐标都乘以-1,纵坐标不变得到点A′,B′,C′,然后描点即可得到△A′B′C′,如果利用坐标特征可判断△A′B′C′与△ABC关于y轴对称.
【详解】
解:如图,△A′B′C′与△ABC关于y轴对称.
【点睛】
本题考查了关于x轴、y轴对称的点的坐标:点P(x,y)关于x轴的对称点P′的坐标是(x,-y);点P(x,y)关于y轴的对称点P′的坐标是(-x,y).
19.(1) E(-3, -1)、F(6, -1)、G(4,4); (2)false
【分析】
(1)根据点的坐标平移规律即可得△EFG的三个顶点坐标;(2)利用三角形的面积公式求解即可.
【详解】
(1)将A(-5,0),B(4,0),C(2,5)沿x轴正方向平移2个单位长度,再沿y轴沿负方向平移1个单位长度,根据点的坐标平移规律可得:E(-5+2,0-1)、F(4+2,0-1)、G(2+2,5-1) ,
即: E(-3, -1)、F(6, -1)、G(4,4);
(2)false.
【点睛】
本题主要考查了图象的平移以及点的坐标确定方法,根据平移性质正确平移三角形是解决问题的关键.
20.(1)作图如下:
(2)四边形ABCD的周长为false.
【详解】
试题分析:(1)根据四边形ABCD是以直线MN为对称轴的轴对称图形,分别得出对称点画出即可;
(2)根据勾股定理求出四边形ABCD的周长即可.
试题解析:(1)如图所示:
(2)四边形ABCD的周长为:AB+BC+CD+AD=false.
21.(1)见解析,A1(3,-4),B1(1,0),C1(6,-1);(2)false ;(3)见解析
【分析】
(1)首先根据坐标点结合坐标系确定A、B、C三点位置,再连接可得△ABC,分别作出三个顶点关于x轴的对称点,再顺次连接即可得false;
(2)利用长方形的面积减去false三个顶点上三个直角三角形的面积即可;
(3)作点B关于y轴的对称点B',连接AB'与y轴相交于点P,即点P为所求作的点.
【详解】
(1)如图所示;A1(3,-4),B1(1,0),C1(6,-1)
(2)false
所以false ;
(3)如图所示:作点B关于y轴的对称点B',连接AB'与y轴相交于点P,即点P为所求作的点.
【点睛】
此题主要考查了作图??轴对称与坐标变化、求平面直角坐标系内图形的面积和求最值问题.解决此类的关键是正确确定图形关键点的对称点的位置,掌握求平面直角坐标系内图形的面积的基本方法,以及由两点之间线段最短求最值的具体要求.
22.(1)2;(2)6;(3)10+2.
【详解】
试题分析:(1)根据两点间的距离公式可以解答本题;
(2)根据两点之间线段最短和点的对称可以解答本题;
(3)根据两点之间线段最短和点的对称可以解答本题.
解:(1)∵A(1,4)、B(7,2),
∴AB=
=
=2,
即A、B两点的距离为:2;
(2)如右图1所示,
作点A关于x轴的对称点A′,
∵A(1,4)、B(7,2),
∴A′(1,﹣4),
∴A′B==6,
即PA+PB的最短长度是6;
(3)作点A关于y轴的对称点A′,作点B关于x轴的对称点B′,连接A′B′于y轴交于点N,与x轴交于点M,如图2所示,
∵A(1,4)、B(7,2),
∴A′(﹣1,4),B′(7,﹣2),
∴AB==2,
A′B′==10,
∴四边形ANMB的最小周长是10+2.
【点评】本题考查轴对称﹣最短路径问题,坐标与图形性质,解题的关键是明确题意,利用数形结合的思想解答.
第三章位置与坐标
一、单选题(在下列各题的四个选项中,只有一项是符合题意的.本题共10个小题)
1.某次大型活动由大学生组成仪仗队,若同学甲站在第六行第八列,可以表示为(6,8),则乙同学站第20行第7列,表示为( )
A.(7,20) B.(20,7) C.(7,7) D.(20,20)
2.如图所示,小明从家到达学校要穿过一个居民小区,小区的道路均是正南或正东方向,小明走下面( )线路不能到达学校.
473265572390A.(0,4)→(0,0)→(4,0)
B.(0,4)→(4,4)→(4,0)
C.(0,4)→(1,4)→(1,1)→(4,1)→(4,0)
D.(0,4)→(3,4)→(4,2)→(4,0)
3.点false关于false轴对称的点false的坐标是( )
A.false B.false C.false D.false
4.如图,小手盖住的点的坐标可能为( )
A.(5,2) B.(-6,3) C.(-4,-6) D.(3,-4)
4题图 7题图
5.若点false满足false,则点M所在象限是( )
A.第一、三象限 B.第二、四象限 C.第一、二象限 D.不能确定
6.已知点A(4,2),B(-2,2),则直线AB ( )
A.平行于x轴 B.平行于y轴 C.经过原点 D.以上都有可能
7.如图,一艘海轮位于灯塔P的南偏东70°方向的M处, 它以每小时40海里的速度向正北方向航行,2小时后到 达位于灯塔P的北偏东40°的N处,则N处与灯塔P的 距离为
A.40海里 B.60海里 C.70海里 D.80海里
8.把△ABC各顶点的横坐标都乘以﹣1,纵坐标都不变,所得图形是下列答案中的( )
A. B. C. D.
二、填空题
9.小丽在小明的北偏西30°方向70米处,那么有人向小丽问小明的位置时,小丽应该说:小明在我的___________处.
10.P(x,y)点在第三象限,且 P 点到 x 轴的距离为 3,到 y 轴的距离为 2,则 P 点的坐标为_____.
11.如果 false,那么 false 在第__________象限.
12.已知点false在y轴上,点false在x轴上,则false的值为_____.
13.如图,点A在平面直角坐标系中的位置如图所示,距原点false个单位长度,则点A的坐标是________.
13题图 14题图
14.在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当点B的横坐标为4时,m的值是_____.当点B的横坐标为4n(n为正整数)时,m=_____(用含n的代数式表示)
15.如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A4n+1(n为自然数)的坐标为 (用n表示)
16.(2016湖南省岳阳市)如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长,P1,P2,P3,…,均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,﹣1),P5(﹣1,﹣1),P6(﹣1,2)…根据这个规律,点P2016的坐标为________________________.
三、解答题
44538901968517.false在方格中的位置如图所示.
(1)请在方格纸上(小方格的边长为1)建立平面直角坐标系,使得A、B两点的坐标分别为false,false.并求出C点的坐标;
(2)作出false关于x轴对称的false,并写出false、false两点的坐标.
(3)求false的面积。
18.如图,将false各顶点的横坐标都乘以false,纵坐标不变,请在平面直角坐标系中描出对应的点false,false,false,并依次连接这三个点,则所得到的false与原false有怎样的位置关系?
413194515621019.如图,在△ABC中,三个顶点的坐标分别为A(-5,0),B(4,0),C(2,5),将△ABC沿x轴正方向平移2个单位长度,再沿y轴沿负方向平移1个单位长度得到△EFG.
(1)求△EFG的三个顶点坐标.
(2)求△EFG的面积.
449643527178020.如图.在每个小正方形的边长均为1个单位长度的方格纸中,有线段AB和直线MN,点A、B、M、N均在小正方形的顶点上.
(1)在方格纸中画四边形ABCD(四边形的各顶点均在小正方形的顶点上),使四边形ABCD是以直线MN为对称轴的轴对称图形,点A的对称点为点D,点B的对称点为点C;
(2)请直接写出四边形ABCD的周长.
21.在平面直角坐标系中,已知点false、false、false.
(1)在图中作出false关于x轴对称的false,并写出点false的坐标(直接写答案)
(2)求false的面积;
(3)在y轴上画出点false,使false最小.
22.阅读下列一段文字:已知在平面内两点P1(x1,y1)、P2(x2、y2),其两点间的距离P1P2=
问题解决:已知A(1,4)、B(7,2)
(1)试求A、B两点的距离;
(2)在x轴上找一点P(不求坐标,画出图形即可),使PA+PB的长度最短,求出PA+PB的最短长度;
(3)在x轴上有一点M,在Y轴上有一点N,连接A、N、M、B得四边形ANMB,若四边形ANMB的周长最短,请找到点M、N(不求坐标,画出图形即可),求出四边形ANMB的最小周长.
参考答案
1.B
【详解】
试题分析:根据题意可知行与列的表示为(行数,列数),因此可知第20行第7列表示为(20,7).
故选B
考点:坐标系
2.D
【解析】
【分析】根据题意,在给出的图形中画一下四个选项的行走路线即可得出小明不能到达学校的路线.
【详解】A. (0,4)→(0,0)→(4,0),能到达学校,故不符合题意;
B. (0,4)→(4,4)→(4,0),能到达学校,故不符合题意;
C. (0,4)→(1,4)→(1,1)→(4,1)→(4,0),能到达学校,故不符合题意;
D. (0,4)→(3,4)→(4,2)→(4,0),不能到达学校,故符合题意,
故选D.
【点睛】本题考查了利用坐标确定位置,也考查了数学在生活中的应用,结合题意,自己动手操作一下即可更准确地得到结论.
3.C
【分析】
根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”解答.
【详解】
解:点M(-1,2)关于x轴对称的点的坐标为(-1,-2).
故选:C.
【点睛】
本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数.
4.C
【详解】
根据题意,小手盖住的点在第三象限,结合第三象限点的坐标特点,分析选项可得答案.
解答:解:根据图示,小手盖住的点在第三象限,
第三象限的点坐标特点是:横负纵负;
分析选项可得只有C符合.
故选C.
点评:本题主要考查了点在第三象限时点的坐标特征,比较简单.注意四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
5.B
【分析】
利用完全平方公式展开并整理得到false,从而判断出false、false异号,再根据各象限内点的坐标特征解答.
【详解】
解:false,
false,
false,
false、false异号,
false点false在第二、四象限.
故选:false.
【点睛】
本题考查了完全平方公式,各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键.
6.A
【详解】
A(4,2),B(-2,2)
∴点A到x轴的距离为2,点B到x轴的距离为2
且A、B都在x轴上方
∴AB平行于x轴,故选A.
点睛:此题是研究平面直角坐标系中,两个点所连线段与坐标轴的位置关系,需要对点到直线的距离有着明确地理解,而且此题属于较简单的判断线与坐标轴位置关系的一类问题.
7.D
【详解】
分析:依题意,知MN=40海里/小时×2小时=80海里,
∵根据方向角的意义和平行的性质,∠M=70°,∠N=40°,
∴根据三角形内角和定理得∠MPN=70°.∴∠M=∠MPN=70°.
∴NP=NM=80海里.故选D.
8.A
【分析】
平面直角坐标系中任意一点P(x,y),关于x轴的对称点的坐标是(x,﹣y),关于y轴的对称点的坐标是(﹣x,y),三个顶点坐标的横坐标都乘以﹣1,并保持纵坐标不变,就是横坐标变成相反数.即所得到的点与原来的点关于y轴对称.
【详解】
解:根据轴对称的性质,知将△ABC的三个顶点的横坐标乘以﹣1,就是把横坐标变成相反数,纵坐标不变,
因而是把三角形的三个顶点以y轴为对称轴进行轴对称变换.所得图形与原图形关于y轴对称.
故选A.
【点睛】
本题主要考查了关于y轴对称点的性质,正确应用坐标判断两点关于y轴对称的方法:横坐标互为相反数,纵坐标相同是解题关键.
9.南偏东30°方向70米
【分析】
直接利用方向角的定义分析得出答案.北
【详解】
如图所示:
∵小丽在小明的北偏西30°方向,距离小明70米处,
∴小丽应该说:小明在我的南偏东30°方向70米处.
故答案为:南偏东30°方向 70米.
【点睛】
本题主要考查了用方向角和距离确定物体的位置,正确画出图形是解题关键.
10.(-2,-3)
【分析】
平面直角坐标系中,点到x 轴的距离为是这个点纵坐标的绝对值, 点到y 轴的距离为是这个点横坐标的绝对值,由此解题即可.
【详解】
∵P(x,y)点在第三象限,且 P 点到 x 轴的距离为 3,到 y 轴的距离为 2,
∴由平面直角坐标系各象限点的特征可知,P(-2,-3).
【点睛】
本题考查了平面直角坐标系中,点的特征,属于简单题,理解清楚点的横纵坐标的几何意义是解题关键.
11.三
【分析】
根据绝对值的性质可得false,解得false,再根据各象限内点的坐标特征解答.
【详解】
解:false,
false,
解得false,
false,false,
false在第三象限.
故答案为:三.
【点睛】
本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限false;第二象限false;第三象限false;第四象限false.
12.0
【分析】
根据x轴、y轴上的点的坐标特点可得false,false,即可求出a、b的值,代入即可得答案.
【详解】
∵点false在y轴上,点false在x轴上,
∴false,false,
∴false,false,
∴false.
【点睛】
本题考查坐标系中,x轴、y轴上的点的坐标特点,x轴上的点的纵坐标都为0;y轴上的点的横坐标都为0.
13.false
【分析】
过A作AB⊥x轴于点B,由勾股定理可得AB=OB=2,由勾股定理可得AB=OB=2,进一步可得点A的坐标.
【详解】
解:过A作AB⊥x轴于点B,
∵∠AOB=45°,
∴AB=OB,AO=false
由勾股定理可得AB=OB=2
又∵A在第四象限
∴点A的坐标为(2,-2)
故答案为(2,-2)
【点睛】
本题考查了点的坐标,解题关键是作出图形应用勾股定理求出点到坐标轴的距离.
14.3, 6n﹣3
【分析】
根据题意,分别找出n=1、2、3时的整点的个数,即可发现n增加1,整点的个数增加6,然后写出横坐标为4n时的表达式即可.
【详解】
解:如图,n=1,即点B的横坐标为4时,整点个数为:6×1﹣3=3,
n=2,即点B的横坐标为8时,整点个数为:6×2﹣3=9,
n=3,即点B的横坐标为12时,整点个数为:6×3﹣3=15,
n=4,即点B的横坐标为16时,整点个数为:6×4﹣3=21,
…,
所以,点B的横坐标为4n时,整点个数为6n﹣3.
故答案为3,6n﹣3.
【点睛】
此题主要考查了点的坐标规律,根据图形找出整点个数的变化规律:n增加1,整点的个数增加6是解题的关键.
15.(2n,1)
【详解】
试题分析:根据图形分别求出n=1、2、3时对应的点A4n+1的坐标,然后根据变化规律写出即可:
由图可知,n=1时,4×1+1=5,点A5(2,1),
n=2时,4×2+1=9,点A9(4,1),
n=3时,4×3+1=13,点A13(6,1),
∴点A4n+1(2n,1).
16.(504,﹣504)
【详解】
根据各个点的位置关系,可得出下标为4的倍数的点在第四象限的角平分线上,被4除余1的点在第三象限的角平分线上,被4除余2的点在第二象限的角平分线上,被4除余3的点在第一象限的角平分线上,点P2016在第四象限的角平分线上,且横纵坐标的绝对值=2016÷4,
由规律可得,2016÷4=504,∴点P2016的在第四象限的角平分线上,
∵点P4(1,﹣1),点P8(2,﹣2),点P12(3,﹣3),
∴点P2016(504,﹣504),
故答案为(504,﹣504).
17.(1)画图见解析,false;(2)画图见解析,Bfalse;(3)2.5
【分析】
(1)根据点A的坐标可知坐标原点在点A左边两个单位,上边一个单位,再求出C的坐标即可;
(2)找到与x轴对称的且到x轴的距离为1的A1,同法做其他点的对应点即可得到△ABC关于x轴对称的△A1B1C1.
(3)利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积进行计算求解.
【详解】
(1)建立的平面直角坐标系如下所示:
其中C点的坐标为:C(3,-3);
(2)所作图形如上所示,其中B1,C1的坐标分别为:(1,4),(3,3);
(3)S△ABC=2×3-false×1×3-false×2×1-false×2×1
=6-3.5
=2.5.
【点睛】
本题考查轴对称作图,掌握画图的方法和图形的特点是关键;会根据一个点的坐标得到坐标原点.(3)中求三角形的面积通常都是利用三角形所在的矩形的面积减去四周三角形的面积求解,此方法需要掌握.
18.与原图形关于y轴对称
【分析】
利用△ABC各顶点的横坐标都乘以-1,纵坐标不变得到点A′,B′,C′,然后描点即可得到△A′B′C′,如果利用坐标特征可判断△A′B′C′与△ABC关于y轴对称.
【详解】
解:如图,△A′B′C′与△ABC关于y轴对称.
【点睛】
本题考查了关于x轴、y轴对称的点的坐标:点P(x,y)关于x轴的对称点P′的坐标是(x,-y);点P(x,y)关于y轴的对称点P′的坐标是(-x,y).
19.(1) E(-3, -1)、F(6, -1)、G(4,4); (2)false
【分析】
(1)根据点的坐标平移规律即可得△EFG的三个顶点坐标;(2)利用三角形的面积公式求解即可.
【详解】
(1)将A(-5,0),B(4,0),C(2,5)沿x轴正方向平移2个单位长度,再沿y轴沿负方向平移1个单位长度,根据点的坐标平移规律可得:E(-5+2,0-1)、F(4+2,0-1)、G(2+2,5-1) ,
即: E(-3, -1)、F(6, -1)、G(4,4);
(2)false.
【点睛】
本题主要考查了图象的平移以及点的坐标确定方法,根据平移性质正确平移三角形是解决问题的关键.
20.(1)作图如下:
(2)四边形ABCD的周长为false.
【详解】
试题分析:(1)根据四边形ABCD是以直线MN为对称轴的轴对称图形,分别得出对称点画出即可;
(2)根据勾股定理求出四边形ABCD的周长即可.
试题解析:(1)如图所示:
(2)四边形ABCD的周长为:AB+BC+CD+AD=false.
21.(1)见解析,A1(3,-4),B1(1,0),C1(6,-1);(2)false ;(3)见解析
【分析】
(1)首先根据坐标点结合坐标系确定A、B、C三点位置,再连接可得△ABC,分别作出三个顶点关于x轴的对称点,再顺次连接即可得false;
(2)利用长方形的面积减去false三个顶点上三个直角三角形的面积即可;
(3)作点B关于y轴的对称点B',连接AB'与y轴相交于点P,即点P为所求作的点.
【详解】
(1)如图所示;A1(3,-4),B1(1,0),C1(6,-1)
(2)false
所以false ;
(3)如图所示:作点B关于y轴的对称点B',连接AB'与y轴相交于点P,即点P为所求作的点.
【点睛】
此题主要考查了作图??轴对称与坐标变化、求平面直角坐标系内图形的面积和求最值问题.解决此类的关键是正确确定图形关键点的对称点的位置,掌握求平面直角坐标系内图形的面积的基本方法,以及由两点之间线段最短求最值的具体要求.
22.(1)2;(2)6;(3)10+2.
【详解】
试题分析:(1)根据两点间的距离公式可以解答本题;
(2)根据两点之间线段最短和点的对称可以解答本题;
(3)根据两点之间线段最短和点的对称可以解答本题.
解:(1)∵A(1,4)、B(7,2),
∴AB=
=
=2,
即A、B两点的距离为:2;
(2)如右图1所示,
作点A关于x轴的对称点A′,
∵A(1,4)、B(7,2),
∴A′(1,﹣4),
∴A′B==6,
即PA+PB的最短长度是6;
(3)作点A关于y轴的对称点A′,作点B关于x轴的对称点B′,连接A′B′于y轴交于点N,与x轴交于点M,如图2所示,
∵A(1,4)、B(7,2),
∴A′(﹣1,4),B′(7,﹣2),
∴AB==2,
A′B′==10,
∴四边形ANMB的最小周长是10+2.
【点评】本题考查轴对称﹣最短路径问题,坐标与图形性质,解题的关键是明确题意,利用数形结合的思想解答.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
