三角形中位线定理

(共13张PPT)
教学目标：
1、进一步发展学生的逻辑推理能力 ；
2、掌握三角形中位线定理，能利用中位线定理解决一些实际问题；
3、让学生体会探索、发现问题和解决问题的喜悦心情。
教学重点和难点：
重点：探索三角形中位线定理及应用。
难点：探索三角形中位线定理。
复习：
直角三角形斜边上的中线与斜边的关系？
直角三角形斜边上的中线等于斜边的一半。
AD = DB
AE = EC
DE是△ABC的中位线
连结三角形两边中点的线段叫做三角形的中位线
三角形的中位线共有三条
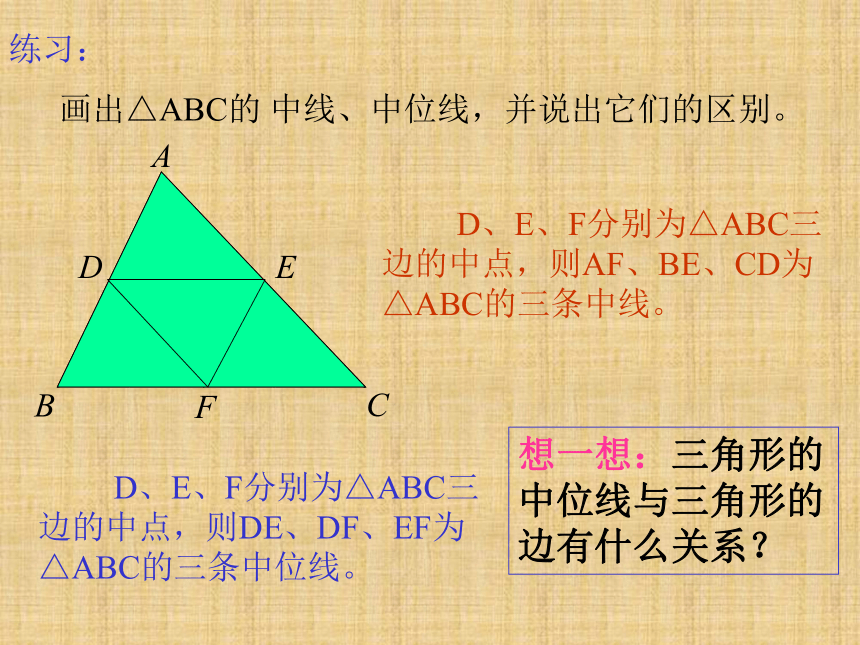
练习：
画出△ABC的 中线、中位线，并说出它们的区别。
D、E、F分别为△ABC三边的中点，则DE、DF、EF为△ABC的三条中位线。
D、E、F分别为△ABC三边的中点，则AF、BE、CD为△ABC的三条中线。
想一想：三角形的中位线与三角形的边有什么关系？
F
A
E
D
C
B
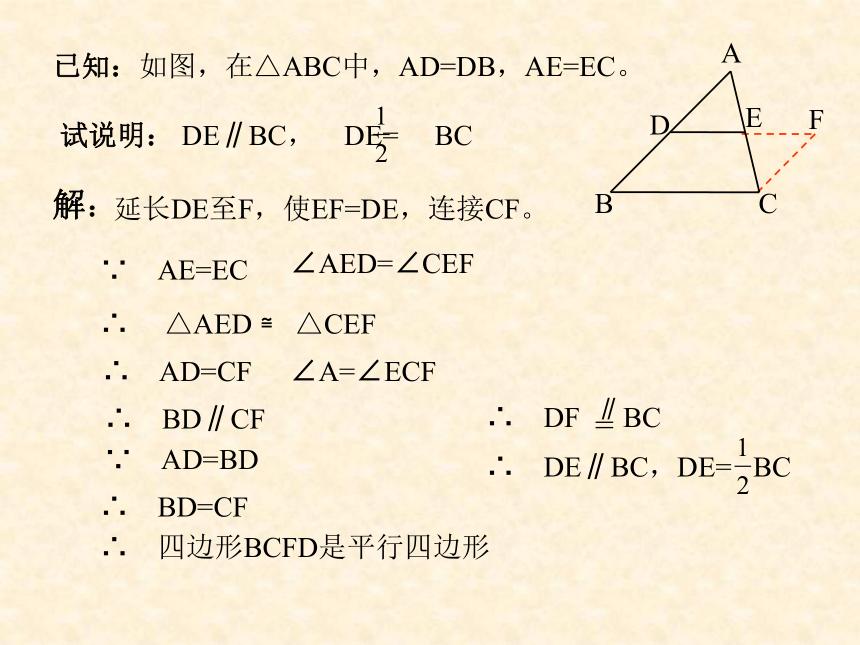
已知：如图，在△ABC中，AD=DB，AE=EC。
试说明： DE∥BC， DE= BC
解：
延长DE至F，使EF=DE，连接CF。
∵　AE=EC
∠AED=∠CEF
∴　 △AED ≌ △CEF
∴　AD=CF
∠A=∠ECF
∴　BD∥CF
∵　AD=BD
∴　BD=CF
∴　四边形BCFD是平行四边形
∴　DF BC
∥
=
∴　DE∥BC，DE= BC
三角形的中位线平行于第三边，并且等于第三边的一半。
定理
做一做
如图，任意作一个四边形，并将其四边的中点依次
连接起来，得到一个新的四边形，这个四边形EFGH有
什么特征？请证明你的结论，并与同伴进行交流。
A
H
M
F
E
D
C
B
解：四边形EFGH是平行四边形
理由：连接BD
∵H、F为DC与BC的中点
∴HF＝ BD HF∥BD
同理：∴ME＝ BD ME∥BD
∴ME=HF ME∥HF
∴四边形EFHM是平行四边形
例: 如图，已知梯形ABCD中，AB∥CD，E、F分别为AD与BC的中点，试说明:EF∥AB∥CD且EF＝ (AB+CD)
G
D
C
E
A
F
B
解：连接DF并延长交AB延长线于点G
∵ DC∥AB 即 DC∥AG
∴ ∠CDF=∠G
又∵ F为BC的中点
∴ CF=BF
又∵ ∠DFC=∠GFB
∴ △DCF≌△GBF
∴ DC=BG DF=GF
又∵ E为AD的中点
∴ AE=DE
∴EF= AG= (AB+BG) 且EF∥GA
∴EF= (AB+BG) 且EF∥AB
又∵ AB∥CD
∴ EF∥AB∥CD 且EF＝ (AB+CD)
练习：
1、求证：三角形的一条中位线与第三边上的中线互相平分。
F
A
B
C
D
E
2、已知；如图，在△ABC中，D是AB边的中点，DE∥BC，
交AC于E。求证；AE=CE。
A
E
D
C
B
Eˊ
A
D
C
B
思考题：
如图，田村有一四边形的池塘，在它的四个角A、B、
C、D处均有一棵大核桃树。田村准备开挖池塘建养鱼池，
想使池塘面积扩大一倍，又想保护核桃树不动，要求扩建
后的池塘成平行四边形状。请问田村能否实现这一设想？
若能，请你设计并画出图形；若不能，请说明理由。
H
G
F
E
1、本节主要学习了三角形中位线定理。
定理 三角形的中位线平行于第三边，并且等于第三边的一半。
3、若题中含有中点或隐含中点的条件时，常构造三角形中位线
解决问题。
2、利用三角形的中位线是证明线段的平行和倍分问题的方
法之一。
作业：P85习题3.3第1、3、4题。
4、在解决四边形的有关问题时，常常连接对角线把四边形转
化为三角形解决。
小结：
再见！
好好学习
天天向上