3.3 勾股定理的应用举例 同步练习(含解析)
文档属性
| 名称 | 3.3 勾股定理的应用举例 同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 12:59:41 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第三章 勾股定理
3 勾股定理的应用举例
知识能力全练
知识点一 确定几何体上的最短路线
1.将一根24 cm长的筷子置于底面直径为15 cm,高8 cm的装满水的无盖圆柱形水杯中,设筷子浸没在水里的长度为h cm,则h的取值范围是( )
A.h≤15 B.h≥8 C.8≤h≤17 D.7≤h≤16
2.下图是一个底面为等边三角形的三棱柱,为了漂亮,小丽在三棱柱的侧面上,从顶点A到顶点A′镶上一圈金属丝,已知此三棱柱的高为5cm,底面边长为4cm,则这圈金属丝的长度至少为( )
A.8 cm B.13 cm C.12 cm D.15 cm
3.如图所示,长方体盒子(无盖)的长、宽、高分别是12 cm,8 cm,30 cm,在AB中点C处有一滴蜜糖,则一只小虫从D处爬到C处的最短路程是多少?
知识点二 利用直角三角形的判别条件判定垂直
4.李老师想用三根木条做一个直角三角尺作为教具,以下四组木条中,哪一组的三根木条能够刚好做成?( )
A.,, B.5、12、13 C.4、5、6 D.1、2、3
5.如图所示,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里,且已知“远航”号沿东北方向航行,那么“海天”号航行的方向是__________.
知识点三 应用勾股定理解决实际问题
6.如图所示,第9号台风“利奇马”过后,某市体育中心附近一棵大树在高于地面3米处折断,大树顶部落在距离大树底部4米处的地面上那么树高是( )
A.5 m B.8 m C.9 m D.12 m
7.如图所示,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,则船向岸边移动了________米.
8.某市进行老城区道路改造,原来从小明家A地到商场F地需要沿着A→B→C→D→E→F连续多次直角拐弯行进,造成出行困难(行走各段路程数据如图所示),道路改造后可从小明家A地直达商场F地求从小明家到商场的路程比原来缩短了多少米.
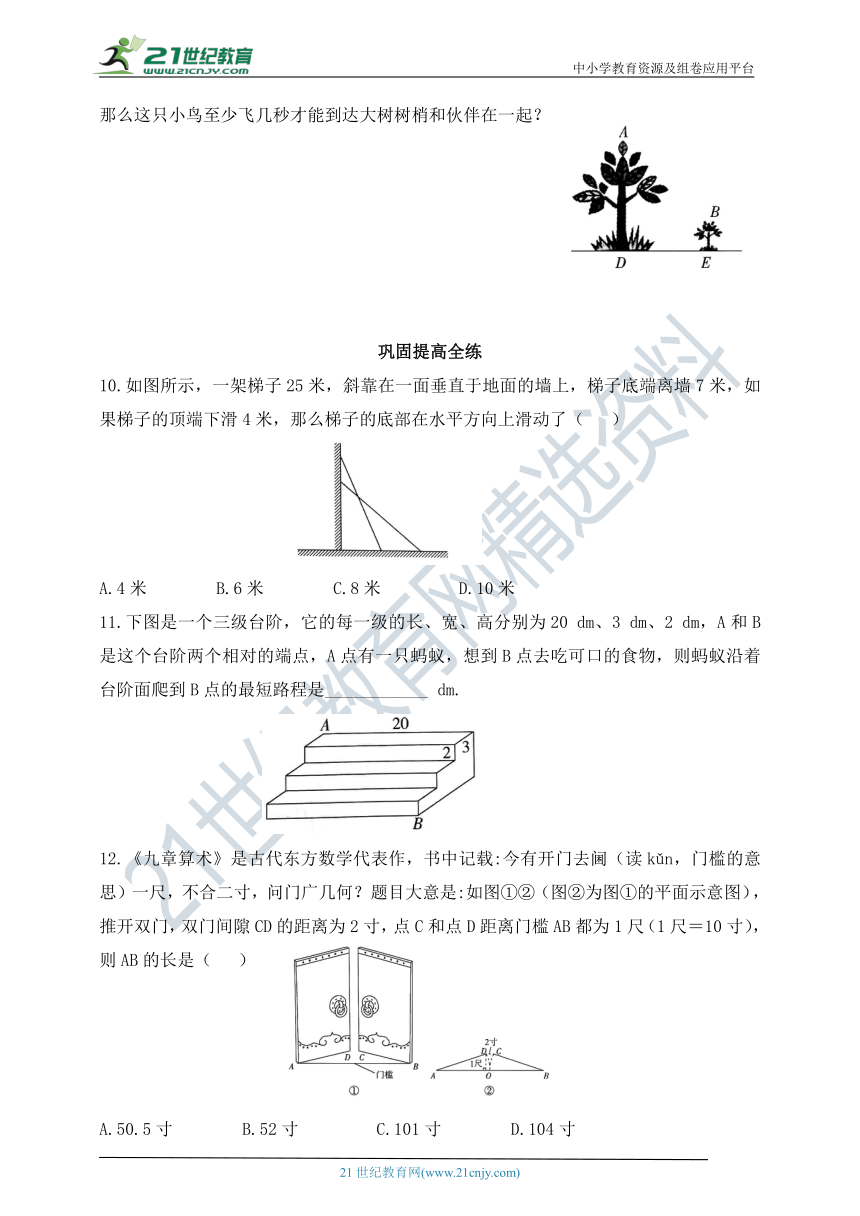
9.如图所示,有一只小鸟在一棵高4 m的小树树梢B处捉虫子,它的伙伴在离该树12 m,高20 m的一棵大树的树梢A处发出友好的叫声,它立刻以4 m/s的速度飞向大树树梢,那么这只小鸟至少飞几秒才能到达大树树梢和伙伴在一起?
巩固提高全练
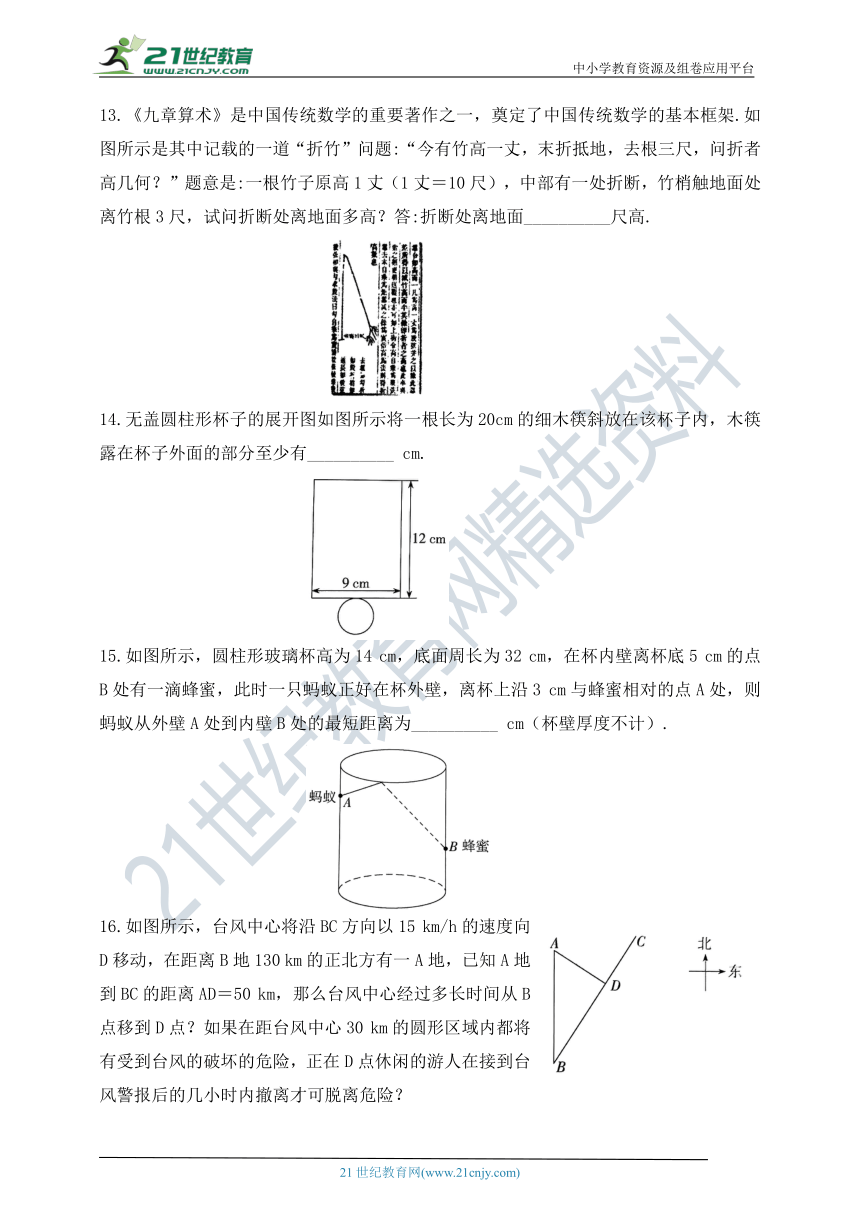
10.如图所示,一架梯子25米,斜靠在一面垂直于地面的墙上,梯子底端离墙7米,如果梯子的顶端下滑4米,那么梯子的底部在水平方向上滑动了( )
A.4米 B.6米 C.8米 D.10米
11.下图是一个三级台阶,它的每一级的长、宽、高分别为20 dm、3 dm、2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是____________ dm.
12.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图①②(图②为图①的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
13.《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面__________尺高.
14.无盖圆柱形杯子的展开图如图所示将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有__________ cm.
15.如图所示,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为__________ cm(杯壁厚度不计).
16.如图所示,台风中心将沿BC方向以15 km/h的速度向D移动,在距离B地130 km的正北方有一A地,已知A地到BC的距离AD=50 km,那么台风中心经过多长时间从B点移到D点?如果在距台风中心30 km的圆形区域内都将有受到台风的破坏的危险,正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?
17.如图所示,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为400 m,200 m,且CD=800 m,牧童从A处把牛牵到河边饮水后再回家问在何处饮水牧童所走的路程最短?最短路程是多少?
参考答案
1.C 2.B
3.解析 将长方体的前面和右侧面展开至同一平面,如图,连接DC,则DC的长就是从D处爬到C处的最短路程.
在Rt△DAC中,AD=12+8=20(cm),AC=×30=15(cm),
由勾股定理得DC=25cm.
故从D处爬到C处的最短路程是25cm.
4.B 5.西北方向 6.B 7.9
8.解析 如图所示,过点A作AH⊥EF于H,
则在Rt△AHF中,AH=40+40=80(米),
FH=70-20+10=60(米),由勾股定理得AF=100米,
故改造后小明家与商场的距离为100米,
改造前小明家与商场的距离为10+40+20+40+70=180(米),
缩短距离:180-100=80(米).
答:从小明家到商场的路程比原来缩短了80米.
9.解析 如图所示,根据题意,得AC=20-4=16m,BC=12m.
根据勾股定理,得AB=20m.
故小鸟所用的时间至少是20÷4=5(s).
10.C 11. 25 12.C 13. 4.55 14. 5 15. 20
16.解析 在Rt△ABD中,根据勾股定理,得BD2=AB2-AD2=1302-502=14400,∴BD=120km,
则台风中心经过120÷15=8小时从B移动到D点.
如图,∵距台风中心30km的圆形区域内都会受到台风的影响,
∴人们要在台风中心到达E点之前撤离,∵BE=BD-DE=120-30=90km,
∴游人在=6小时内撤离才可脱离危险.
17.解析 如图所示,作点A关于直线l的对称点G,连接GB交CD于点E,连接AE,则在E处饮水牧童所走的路程最短.
理由:
在直线CD上任意取一异于点E的点I,连接AI,B1,GI.
∵点G,A关于直线对称,∴AI=GI,AE=GE,
∴AI+BI=GI+BI,AE+BE=GE+BE=GB.
由“两点之间线段最短”和“三角形任意两边之和大于第三边”可得GI+BI>GB=AE+BE,∴在E处饮水牧童所走路程最短,最短路程为GB的长.
过点G作BD的垂线,与BD的延长线交于点H.
∵GH=CD=800 m, BH= BD+DH=BD+GC=BD+AC=200+400=600m,
∴在Rt△GHB中,由勾股定理,得GB2=GH2+BH2=8002+6002=10002.
∴GB=1000m,即最短路程为1000m.
_21?????????è?????(www.21cnjy.com)_
第三章 勾股定理
3 勾股定理的应用举例
知识能力全练
知识点一 确定几何体上的最短路线
1.将一根24 cm长的筷子置于底面直径为15 cm,高8 cm的装满水的无盖圆柱形水杯中,设筷子浸没在水里的长度为h cm,则h的取值范围是( )
A.h≤15 B.h≥8 C.8≤h≤17 D.7≤h≤16
2.下图是一个底面为等边三角形的三棱柱,为了漂亮,小丽在三棱柱的侧面上,从顶点A到顶点A′镶上一圈金属丝,已知此三棱柱的高为5cm,底面边长为4cm,则这圈金属丝的长度至少为( )
A.8 cm B.13 cm C.12 cm D.15 cm
3.如图所示,长方体盒子(无盖)的长、宽、高分别是12 cm,8 cm,30 cm,在AB中点C处有一滴蜜糖,则一只小虫从D处爬到C处的最短路程是多少?
知识点二 利用直角三角形的判别条件判定垂直
4.李老师想用三根木条做一个直角三角尺作为教具,以下四组木条中,哪一组的三根木条能够刚好做成?( )
A.,, B.5、12、13 C.4、5、6 D.1、2、3
5.如图所示,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里,且已知“远航”号沿东北方向航行,那么“海天”号航行的方向是__________.
知识点三 应用勾股定理解决实际问题
6.如图所示,第9号台风“利奇马”过后,某市体育中心附近一棵大树在高于地面3米处折断,大树顶部落在距离大树底部4米处的地面上那么树高是( )
A.5 m B.8 m C.9 m D.12 m
7.如图所示,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,则船向岸边移动了________米.
8.某市进行老城区道路改造,原来从小明家A地到商场F地需要沿着A→B→C→D→E→F连续多次直角拐弯行进,造成出行困难(行走各段路程数据如图所示),道路改造后可从小明家A地直达商场F地求从小明家到商场的路程比原来缩短了多少米.
9.如图所示,有一只小鸟在一棵高4 m的小树树梢B处捉虫子,它的伙伴在离该树12 m,高20 m的一棵大树的树梢A处发出友好的叫声,它立刻以4 m/s的速度飞向大树树梢,那么这只小鸟至少飞几秒才能到达大树树梢和伙伴在一起?
巩固提高全练
10.如图所示,一架梯子25米,斜靠在一面垂直于地面的墙上,梯子底端离墙7米,如果梯子的顶端下滑4米,那么梯子的底部在水平方向上滑动了( )
A.4米 B.6米 C.8米 D.10米
11.下图是一个三级台阶,它的每一级的长、宽、高分别为20 dm、3 dm、2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是____________ dm.
12.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图①②(图②为图①的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
13.《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面__________尺高.
14.无盖圆柱形杯子的展开图如图所示将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有__________ cm.
15.如图所示,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为__________ cm(杯壁厚度不计).
16.如图所示,台风中心将沿BC方向以15 km/h的速度向D移动,在距离B地130 km的正北方有一A地,已知A地到BC的距离AD=50 km,那么台风中心经过多长时间从B点移到D点?如果在距台风中心30 km的圆形区域内都将有受到台风的破坏的危险,正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?
17.如图所示,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为400 m,200 m,且CD=800 m,牧童从A处把牛牵到河边饮水后再回家问在何处饮水牧童所走的路程最短?最短路程是多少?
参考答案
1.C 2.B
3.解析 将长方体的前面和右侧面展开至同一平面,如图,连接DC,则DC的长就是从D处爬到C处的最短路程.
在Rt△DAC中,AD=12+8=20(cm),AC=×30=15(cm),
由勾股定理得DC=25cm.
故从D处爬到C处的最短路程是25cm.
4.B 5.西北方向 6.B 7.9
8.解析 如图所示,过点A作AH⊥EF于H,
则在Rt△AHF中,AH=40+40=80(米),
FH=70-20+10=60(米),由勾股定理得AF=100米,
故改造后小明家与商场的距离为100米,
改造前小明家与商场的距离为10+40+20+40+70=180(米),
缩短距离:180-100=80(米).
答:从小明家到商场的路程比原来缩短了80米.
9.解析 如图所示,根据题意,得AC=20-4=16m,BC=12m.
根据勾股定理,得AB=20m.
故小鸟所用的时间至少是20÷4=5(s).
10.C 11. 25 12.C 13. 4.55 14. 5 15. 20
16.解析 在Rt△ABD中,根据勾股定理,得BD2=AB2-AD2=1302-502=14400,∴BD=120km,
则台风中心经过120÷15=8小时从B移动到D点.
如图,∵距台风中心30km的圆形区域内都会受到台风的影响,
∴人们要在台风中心到达E点之前撤离,∵BE=BD-DE=120-30=90km,
∴游人在=6小时内撤离才可脱离危险.
17.解析 如图所示,作点A关于直线l的对称点G,连接GB交CD于点E,连接AE,则在E处饮水牧童所走的路程最短.
理由:
在直线CD上任意取一异于点E的点I,连接AI,B1,GI.
∵点G,A关于直线对称,∴AI=GI,AE=GE,
∴AI+BI=GI+BI,AE+BE=GE+BE=GB.
由“两点之间线段最短”和“三角形任意两边之和大于第三边”可得GI+BI>GB=AE+BE,∴在E处饮水牧童所走路程最短,最短路程为GB的长.
过点G作BD的垂线,与BD的延长线交于点H.
∵GH=CD=800 m, BH= BD+DH=BD+GC=BD+AC=200+400=600m,
∴在Rt△GHB中,由勾股定理,得GB2=GH2+BH2=8002+6002=10002.
∴GB=1000m,即最短路程为1000m.
_21?????????è?????(www.21cnjy.com)_
