《11.1与三角形有关的线段》同步能力提升训练(附答案)2021-2022学年八年级数学人教版上册
文档属性
| 名称 | 《11.1与三角形有关的线段》同步能力提升训练(附答案)2021-2022学年八年级数学人教版上册 |  | |
| 格式 | doc | ||
| 文件大小 | 134.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 10:17:35 | ||
图片预览


文档简介
2021年人教版八年级数学上册《11.1与三角形有关的线段》同步能力提升训练(附答案)
1.如图,图中三角形的个数共有( )
A.3个 B.4个 C.5个 D.6个
2.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是锐角三角形 B.都是直角三角形
C.都是钝角三角形 D.是一个锐角三角形和一个钝角三角形
3.已知AD为△ABC的中线,且AB=10cm,AC=8cm,则△ABD与△ACD的周长之差为( )
A.2cm B.4cm C.6cm D.18cm
4.如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中正确的是( )
A.△ABC中,AD是BC边上的高 B.△ABC中,GC是BC边上的高
C.△GBC中,CF是BC边上的高 D.△GBC中,GC是BG边上的高
5.如图,∠BAD=∠ADC=90°,以AD为一条高线的三角形个数有( )
A.2个 B.3个 C.4个 D.5个
6.在△ABC中,作出AC边上的高,正确的是( )
A.① B.② C.③ D.④
7.若AD是△ABC的中线,则下列结论正确的是( )
A.AD⊥BC B.BD=CD C.∠BAD=∠CAD D.AD=BC
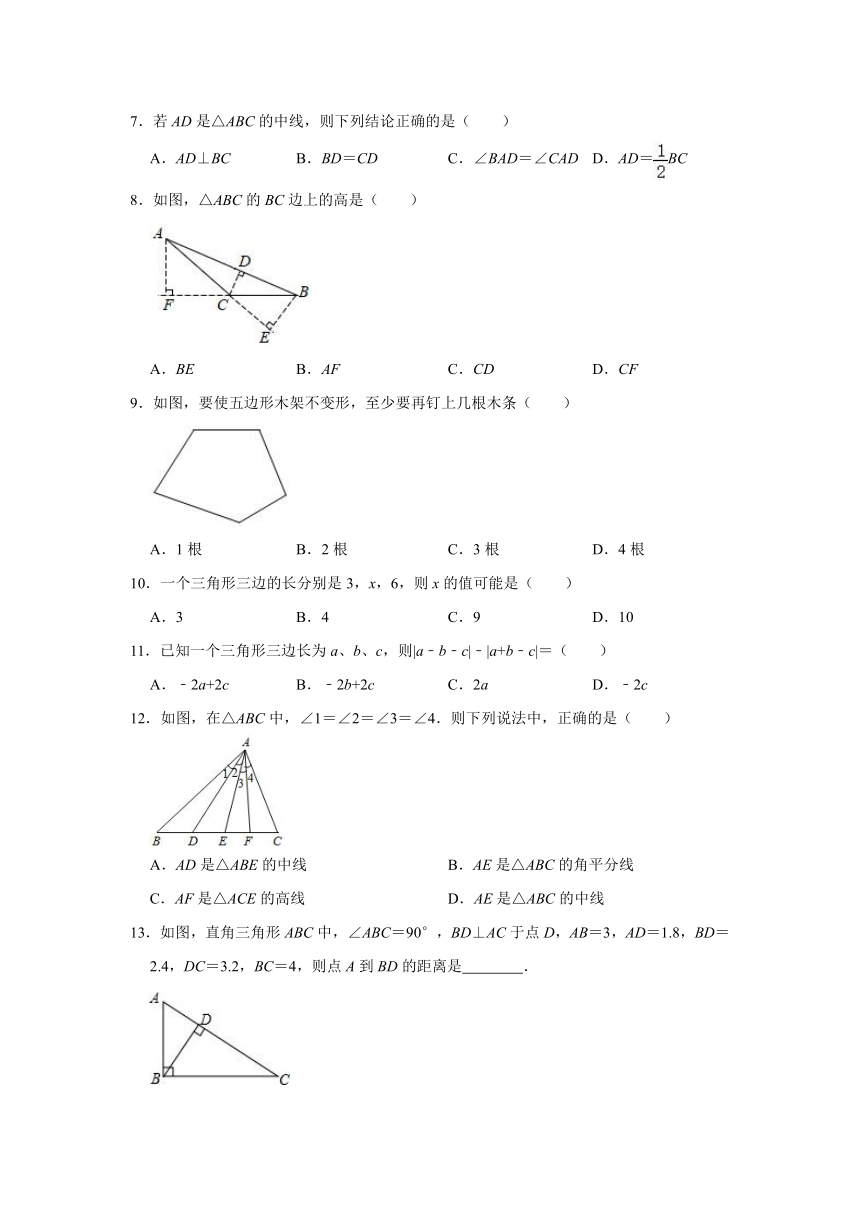
8.如图,△ABC的BC边上的高是( )
A.BE B.AF C.CD D.CF
9.如图,要使五边形木架不变形,至少要再钉上几根木条( )
A.1根 B.2根 C.3根 D.4根
10.一个三角形三边的长分别是3,x,6,则x的值可能是( )
A.3 B.4 C.9 D.10
11.已知一个三角形三边长为a、b、c,则|a﹣b﹣c|﹣|a+b﹣c|=( )
A.﹣2a+2c B.﹣2b+2c C.2a D.﹣2c
12.如图,在△ABC中,∠1=∠2=∠3=∠4.则下列说法中,正确的是( )
A.AD是△ABE的中线 B.AE是△ABC的角平分线
C.AF是△ACE的高线 D.AE是△ABC的中线
13.如图,直角三角形ABC中,∠ABC=90°,BD⊥AC于点D,AB=3,AD=1.8,BD=2.4,DC=3.2,BC=4,则点A到BD的距离是 .
14.如图,AD为△ABC的中线,AB=13cm,AC=10cm.若△ACD的周长28cm,则△ABD的周长为 .
15.若a,b,c为三角形的三边长,此三角形周长为18cm,且a+b=2c,b=2a;则a= cm,b= cm,c= cm.
16.已知a,b,c分别为△ABC的三边,且满足a+b=3c﹣2,a﹣b=2c﹣6.
(1)求c的取值范围;
(2)若△ABC的周长为12,求c的值.
17.已知a=m2+n2,b=m2,c=mn,且m>n>0.
(1)比较a,b,c的大小;
(2)请说明以a,b,c为边长的三角形一定存在.
18.已知:如图,△ABC中,AD、AE分别是△ABC的高和角平分线,BF是∠ABC的平分线,BF与AE交于O,若∠ABC=40°,∠C=60°,求∠DAE、∠BOE的度数.
19.如图,△ACB中,∠ACB=90°,∠1=∠B.
(1)试说明CD是△ABC的高;
(2)如果AC=8,BC=6,AB=10,求CD的长.
20.如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上,三角形BDE与四边形ACDE的周长相等.
(1)求线段AE的长.
(2)若图中所有线段长度的和是53cm,求BC+DE的值.
参考答案
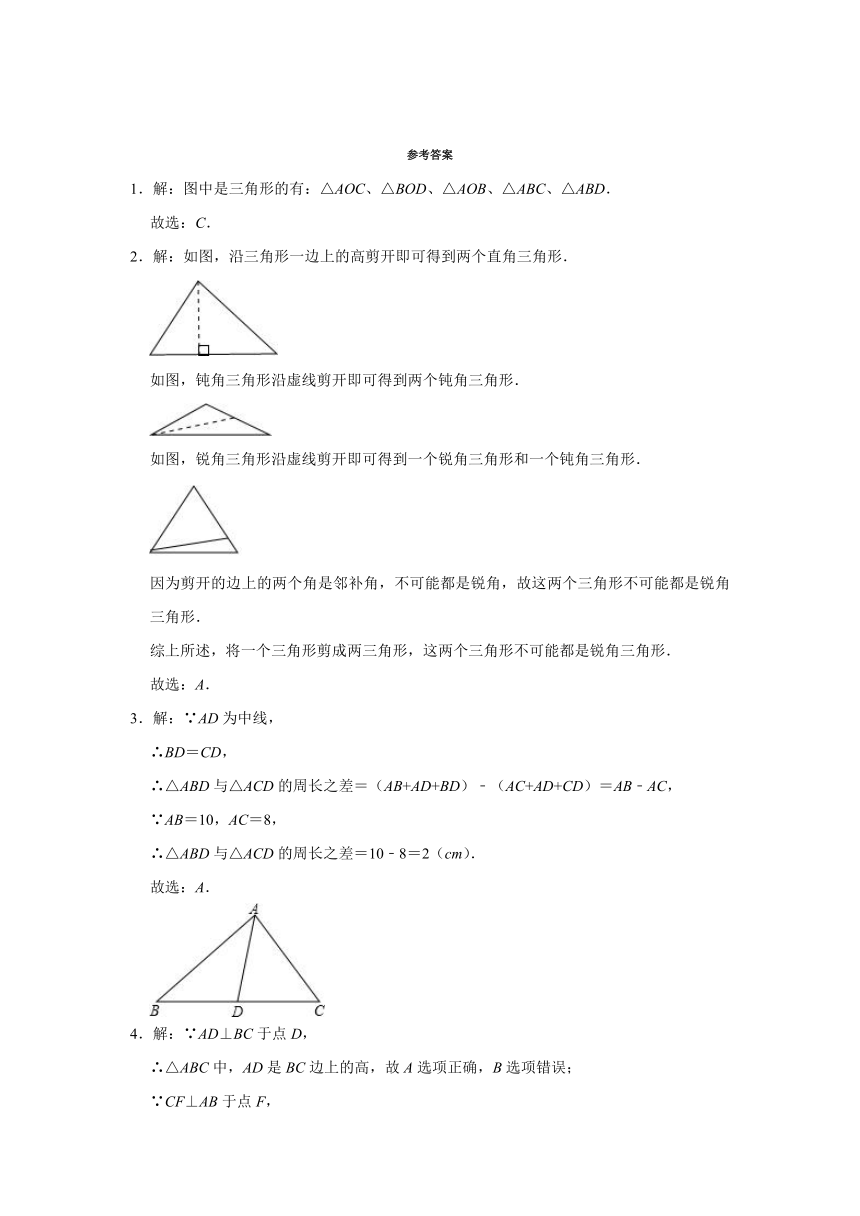
1.解:图中是三角形的有:△AOC、△BOD、△AOB、△ABC、△ABD.
故选:C.
2.解:如图,沿三角形一边上的高剪开即可得到两个直角三角形.
如图,钝角三角形沿虚线剪开即可得到两个钝角三角形.
如图,锐角三角形沿虚线剪开即可得到一个锐角三角形和一个钝角三角形.
因为剪开的边上的两个角是邻补角,不可能都是锐角,故这两个三角形不可能都是锐角三角形.
综上所述,将一个三角形剪成两三角形,这两个三角形不可能都是锐角三角形.
故选:A.
3.解:∵AD为中线,
∴BD=CD,
∴△ABD与△ACD的周长之差=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC,
∵AB=10,AC=8,
∴△ABD与△ACD的周长之差=10﹣8=2(cm).
故选:A.
4.解:∵AD⊥BC于点D,
∴△ABC中,AD是BC边上的高,故A选项正确,B选项错误;
∵CF⊥AB于点F,
∴△GBC中,CF是BG边上的高,故C选项错误,D选项错误.
故选:A.
5.解:以AD为一条高线的三角形有△ADE、△ADC、△AEC、△DAB这4个,
故选:C.
6.解:根据三角形高线的定义,AC边上的高是过点B向AC作垂线垂足为D,
纵观各图形,①、②、③都不符合高线的定义,
④符合高线的定义.
故选:D.
7.解:∵AD是△ABC的中线,
∴BD=DC,
故选:B.
8.解:△ABC的BC边上的高是AF,
故选:B.
9.解:如图,根据三角形的稳定性可知,要使五边形木架不变形,至少要再钉上2根木条,
故选:B.
10.解:根据三角形的三边关系,得:6﹣3<x<6+3,即:3<x<9.
故选:B.
11.解:∵a、b、c是一个三角形三边长,
∴b+c>a,a+b>c,
∴|a﹣b﹣c|﹣|a+b﹣c|
=﹣(a﹣b﹣c)﹣(a+b﹣c)
=﹣a+b+c﹣a﹣b+c
=﹣2a+2c,
故选:A.
12.解:∵∠1=∠2=∠3=∠4,
∴∠1+∠2=∠3+∠4,
即∠BAE=∠CAE,
∴AE是△ABC的角平分线,
故选:B.
13.解:∵BD⊥AC,AD=1.8,
∴点A到BD的距离为1.8,
故答案为:1.8.
14.解:∵AD为△ABC的中线,
∴BD=DC,
∵△ACD的周长28cm,
∴AC+AD+CD=28(cm),
∵AC=10cm,
∴AD+CD=18(cm),即AD+BD=18(cm),
∵AB=13cm,
∴△ABD的周长=AB+AD+BD=31(cm),
故答案为:31cm.
15.解:由题意得,将②代入①,得c=6,
则,解得,
∴方程组的解为.
16.解:(1)∵a,b,c分别为△ABC的三边,a+b=3c﹣2,a﹣b=2c﹣6,
∴,
解得:2<c<6.
故c的取值范围为2<c<6;
(2)∵△ABC的周长为12,a+b=3c﹣2,
∴a+b+c=4c﹣2=12,
解得c=3.5.
故c的值是3.5.
17.解:(1)∵a=m2+n2,b=m2,c=mn,且m>n>0,
∴m2+n2>m2>mn,
∴a>b>c;
(2)∵m>n>0,
∴mn>n2,
∴m2+mn>m2+n2,
∴a,b,c为边长的三角形一定存在.
18.解:①在△ABC中,∵∠ABC=40°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=80°.
∵AE是的角平分线,
∴∠EAC=∠BAC=40°.
∵AD是△ABC的高,
∴∠ADC=90°
∴在△ADC中,∠DAC=180°﹣∠ADC﹣∠C=180°﹣90°﹣60°=30°
∴∠DAE=∠EAC﹣∠DAC=40°﹣30°=10°.
②∵BF是∠ABC的平分线,∠ABC=40°,
∴∠FBC=∠ABC=20°,
又∵∠C=60°,
∴∠AFO=80°,
∴∠AOF=180°﹣80°﹣40°=60°,
∴∠BOE=∠AOF=60°.
19.解:(1)∵∠1+∠BCD=90°,∠1=∠B
∴∠B+∠BCD=90°
∴△BDC是直角三角形,即CD⊥AB,
∴CD是△ABC的高;
(2)∵∠ACB=∠CDB=90°
∴S△ABC=AC?BC=AB?CD,
∵AC=8,BC=6,AB=10,
∴CD===.
20.解:(1)∵三角形BDE与四边形ACDE的周长相等,
∴BD+DE+BE=AC+AE+CD+DE,
∵BD=DC,
∴BE=AE+AC,
设AE=x cm,则BE=(10﹣x)cm,
由题意得,10﹣x=x+6.
解得,x=2,
∴AE=2cm;
(2)图中共有8条线段,
它们的和为:AE+EB+AB+AC+DE+BD+CD+BC=2AB+AC+2BC+DE,
由题意得,2AB+AC+2BC+DE=53,
∴2BC+DE=53﹣(2AB+AC)=53﹣(2×10+6)=27,
∴BC+DE=(cm).
1.如图,图中三角形的个数共有( )
A.3个 B.4个 C.5个 D.6个
2.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是锐角三角形 B.都是直角三角形
C.都是钝角三角形 D.是一个锐角三角形和一个钝角三角形
3.已知AD为△ABC的中线,且AB=10cm,AC=8cm,则△ABD与△ACD的周长之差为( )
A.2cm B.4cm C.6cm D.18cm
4.如图,AD⊥BC于点D,GC⊥BC于点C,CF⊥AB于点F,下列关于高的说法中正确的是( )
A.△ABC中,AD是BC边上的高 B.△ABC中,GC是BC边上的高
C.△GBC中,CF是BC边上的高 D.△GBC中,GC是BG边上的高
5.如图,∠BAD=∠ADC=90°,以AD为一条高线的三角形个数有( )
A.2个 B.3个 C.4个 D.5个
6.在△ABC中,作出AC边上的高,正确的是( )
A.① B.② C.③ D.④
7.若AD是△ABC的中线,则下列结论正确的是( )
A.AD⊥BC B.BD=CD C.∠BAD=∠CAD D.AD=BC
8.如图,△ABC的BC边上的高是( )
A.BE B.AF C.CD D.CF
9.如图,要使五边形木架不变形,至少要再钉上几根木条( )
A.1根 B.2根 C.3根 D.4根
10.一个三角形三边的长分别是3,x,6,则x的值可能是( )
A.3 B.4 C.9 D.10
11.已知一个三角形三边长为a、b、c,则|a﹣b﹣c|﹣|a+b﹣c|=( )
A.﹣2a+2c B.﹣2b+2c C.2a D.﹣2c
12.如图,在△ABC中,∠1=∠2=∠3=∠4.则下列说法中,正确的是( )
A.AD是△ABE的中线 B.AE是△ABC的角平分线
C.AF是△ACE的高线 D.AE是△ABC的中线
13.如图,直角三角形ABC中,∠ABC=90°,BD⊥AC于点D,AB=3,AD=1.8,BD=2.4,DC=3.2,BC=4,则点A到BD的距离是 .
14.如图,AD为△ABC的中线,AB=13cm,AC=10cm.若△ACD的周长28cm,则△ABD的周长为 .
15.若a,b,c为三角形的三边长,此三角形周长为18cm,且a+b=2c,b=2a;则a= cm,b= cm,c= cm.
16.已知a,b,c分别为△ABC的三边,且满足a+b=3c﹣2,a﹣b=2c﹣6.
(1)求c的取值范围;
(2)若△ABC的周长为12,求c的值.
17.已知a=m2+n2,b=m2,c=mn,且m>n>0.
(1)比较a,b,c的大小;
(2)请说明以a,b,c为边长的三角形一定存在.
18.已知:如图,△ABC中,AD、AE分别是△ABC的高和角平分线,BF是∠ABC的平分线,BF与AE交于O,若∠ABC=40°,∠C=60°,求∠DAE、∠BOE的度数.
19.如图,△ACB中,∠ACB=90°,∠1=∠B.
(1)试说明CD是△ABC的高;
(2)如果AC=8,BC=6,AB=10,求CD的长.
20.如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上,三角形BDE与四边形ACDE的周长相等.
(1)求线段AE的长.
(2)若图中所有线段长度的和是53cm,求BC+DE的值.
参考答案
1.解:图中是三角形的有:△AOC、△BOD、△AOB、△ABC、△ABD.
故选:C.
2.解:如图,沿三角形一边上的高剪开即可得到两个直角三角形.
如图,钝角三角形沿虚线剪开即可得到两个钝角三角形.
如图,锐角三角形沿虚线剪开即可得到一个锐角三角形和一个钝角三角形.
因为剪开的边上的两个角是邻补角,不可能都是锐角,故这两个三角形不可能都是锐角三角形.
综上所述,将一个三角形剪成两三角形,这两个三角形不可能都是锐角三角形.
故选:A.
3.解:∵AD为中线,
∴BD=CD,
∴△ABD与△ACD的周长之差=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC,
∵AB=10,AC=8,
∴△ABD与△ACD的周长之差=10﹣8=2(cm).
故选:A.
4.解:∵AD⊥BC于点D,
∴△ABC中,AD是BC边上的高,故A选项正确,B选项错误;
∵CF⊥AB于点F,
∴△GBC中,CF是BG边上的高,故C选项错误,D选项错误.
故选:A.
5.解:以AD为一条高线的三角形有△ADE、△ADC、△AEC、△DAB这4个,
故选:C.
6.解:根据三角形高线的定义,AC边上的高是过点B向AC作垂线垂足为D,
纵观各图形,①、②、③都不符合高线的定义,
④符合高线的定义.
故选:D.
7.解:∵AD是△ABC的中线,
∴BD=DC,
故选:B.
8.解:△ABC的BC边上的高是AF,
故选:B.
9.解:如图,根据三角形的稳定性可知,要使五边形木架不变形,至少要再钉上2根木条,
故选:B.
10.解:根据三角形的三边关系,得:6﹣3<x<6+3,即:3<x<9.
故选:B.
11.解:∵a、b、c是一个三角形三边长,
∴b+c>a,a+b>c,
∴|a﹣b﹣c|﹣|a+b﹣c|
=﹣(a﹣b﹣c)﹣(a+b﹣c)
=﹣a+b+c﹣a﹣b+c
=﹣2a+2c,
故选:A.
12.解:∵∠1=∠2=∠3=∠4,
∴∠1+∠2=∠3+∠4,
即∠BAE=∠CAE,
∴AE是△ABC的角平分线,
故选:B.
13.解:∵BD⊥AC,AD=1.8,
∴点A到BD的距离为1.8,
故答案为:1.8.
14.解:∵AD为△ABC的中线,
∴BD=DC,
∵△ACD的周长28cm,
∴AC+AD+CD=28(cm),
∵AC=10cm,
∴AD+CD=18(cm),即AD+BD=18(cm),
∵AB=13cm,
∴△ABD的周长=AB+AD+BD=31(cm),
故答案为:31cm.
15.解:由题意得,将②代入①,得c=6,
则,解得,
∴方程组的解为.
16.解:(1)∵a,b,c分别为△ABC的三边,a+b=3c﹣2,a﹣b=2c﹣6,
∴,
解得:2<c<6.
故c的取值范围为2<c<6;
(2)∵△ABC的周长为12,a+b=3c﹣2,
∴a+b+c=4c﹣2=12,
解得c=3.5.
故c的值是3.5.
17.解:(1)∵a=m2+n2,b=m2,c=mn,且m>n>0,
∴m2+n2>m2>mn,
∴a>b>c;
(2)∵m>n>0,
∴mn>n2,
∴m2+mn>m2+n2,
∴a,b,c为边长的三角形一定存在.
18.解:①在△ABC中,∵∠ABC=40°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=80°.
∵AE是的角平分线,
∴∠EAC=∠BAC=40°.
∵AD是△ABC的高,
∴∠ADC=90°
∴在△ADC中,∠DAC=180°﹣∠ADC﹣∠C=180°﹣90°﹣60°=30°
∴∠DAE=∠EAC﹣∠DAC=40°﹣30°=10°.
②∵BF是∠ABC的平分线,∠ABC=40°,
∴∠FBC=∠ABC=20°,
又∵∠C=60°,
∴∠AFO=80°,
∴∠AOF=180°﹣80°﹣40°=60°,
∴∠BOE=∠AOF=60°.
19.解:(1)∵∠1+∠BCD=90°,∠1=∠B
∴∠B+∠BCD=90°
∴△BDC是直角三角形,即CD⊥AB,
∴CD是△ABC的高;
(2)∵∠ACB=∠CDB=90°
∴S△ABC=AC?BC=AB?CD,
∵AC=8,BC=6,AB=10,
∴CD===.
20.解:(1)∵三角形BDE与四边形ACDE的周长相等,
∴BD+DE+BE=AC+AE+CD+DE,
∵BD=DC,
∴BE=AE+AC,
设AE=x cm,则BE=(10﹣x)cm,
由题意得,10﹣x=x+6.
解得,x=2,
∴AE=2cm;
(2)图中共有8条线段,
它们的和为:AE+EB+AB+AC+DE+BD+CD+BC=2AB+AC+2BC+DE,
由题意得,2AB+AC+2BC+DE=53,
∴2BC+DE=53﹣(2AB+AC)=53﹣(2×10+6)=27,
∴BC+DE=(cm).
