《11.2与三角形有关的角》同步能力提升训练(附答案)2021-2022学年八年级数学人教版上册
文档属性
| 名称 | 《11.2与三角形有关的角》同步能力提升训练(附答案)2021-2022学年八年级数学人教版上册 |

|
|
| 格式 | doc | ||
| 文件大小 | 226.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览


文档简介
2021年人教版八年级数学上册《11.2与三角形有关的角》同步能力提升训练(附答案)
1.如图,在△ABC中,∠A=50°,则∠1+∠2的度数是( )
A.180° B.230° C.280° D.无法确定
2.直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B在射线OM上运动.如图,已知AE,BE分别是∠BAO和∠ABO的角平分线,点A,B在运动的过程中,∠AEB度数为( )
A.120° B.135° C.100° D.无法确定
3.已知∠A、∠B、∠C是△ABC的三个内角,下列条件不能确定△ABC是直角三角形的是( )
A.∠A=40°,∠B=50° B.∠A=90°
C.∠A+∠B=∠C D.∠A+∠B=2∠C
4.如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC和∠ABC的角平分线,它们相交于点O,∠AOB=125°,则∠CAD的度数为( )
A.20° B.30° C.45° D.50°
5.若一个三角形的两个内角的度数分别为60°,50°,则这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能确定
6.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB=∠CGE.
其中正确的结论的个数是( )
A.1 B.2 C.3 D.4
7.将一副学生用三角板(一个锐角为30°的直角三角形,一个锐角为45°的直角三角形)如图叠放,则下列4个结论中正确的个数有( )
①OE平分∠AOD;②∠AOC=∠BOD;③∠AOC﹣∠CEA=15°;
④∠COB+∠AOD=180°.
A.0 B.1 C.2 D.3
8.如图,CD、BD分别平分∠ACE、∠ABC,∠A=80°,则∠BDC=( )
A.35° B.40° C.30° D.45°
9.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=56°,∠2=29°,则∠A的度数为 度.
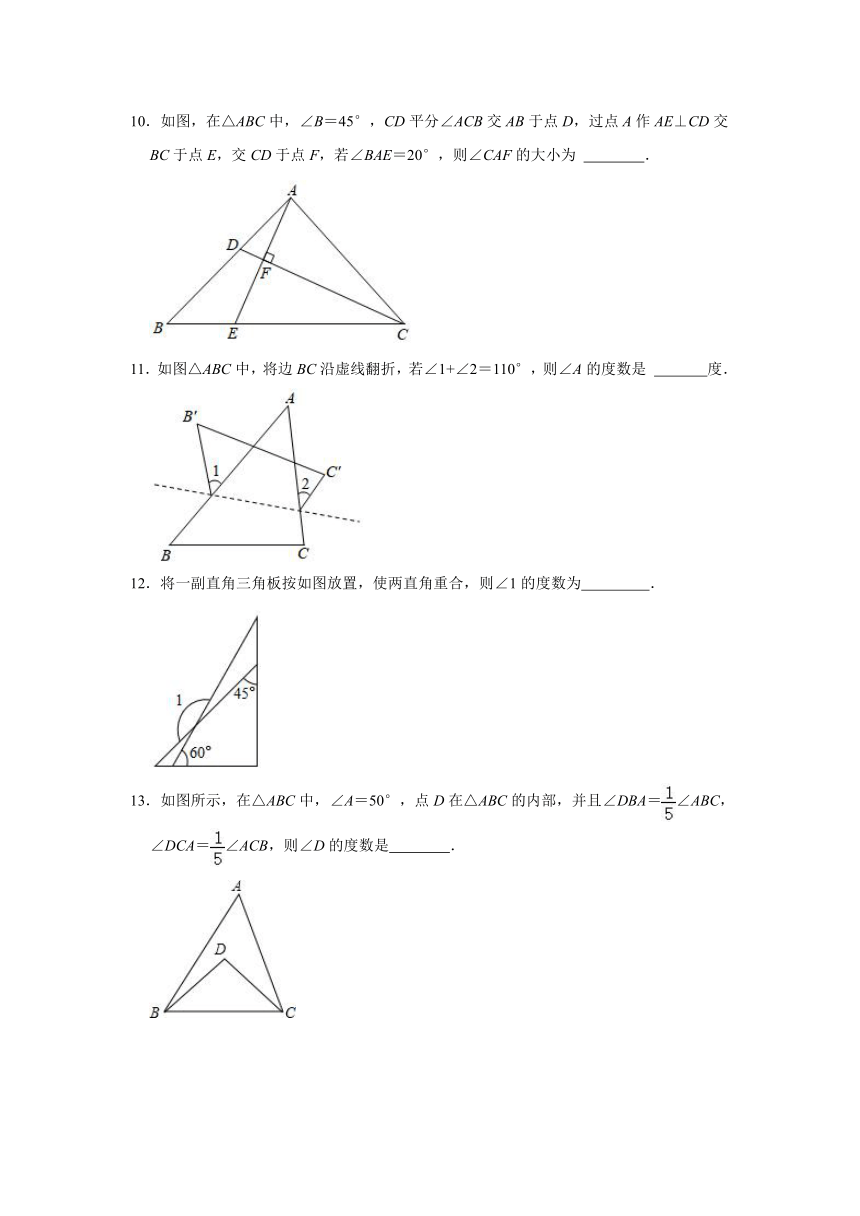
10.如图,在△ABC中,∠B=45°,CD平分∠ACB交AB于点D,过点A作AE⊥CD交BC于点E,交CD于点F,若∠BAE=20°,则∠CAF的大小为 .
11.如图△ABC中,将边BC沿虚线翻折,若∠1+∠2=110°,则∠A的度数是 度.
12.将一副直角三角板按如图放置,使两直角重合,则∠1的度数为 .
13.如图所示,在△ABC中,∠A=50°,点D在△ABC的内部,并且∠DBA=∠ABC,∠DCA=∠ACB,则∠D的度数是 .
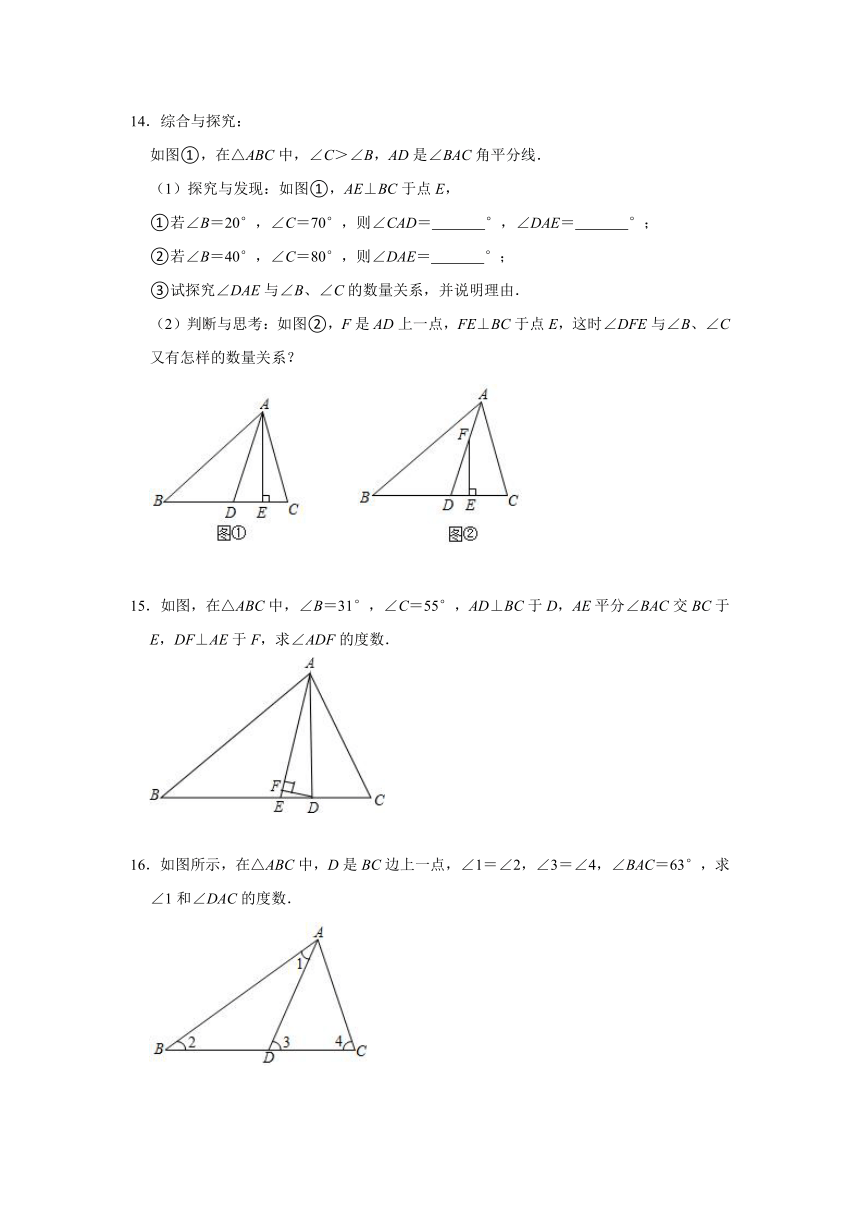
14.综合与探究:
如图①,在△ABC中,∠C>∠B,AD是∠BAC角平分线.
(1)探究与发现:如图①,AE⊥BC于点E,
①若∠B=20°,∠C=70°,则∠CAD= °,∠DAE= °;
②若∠B=40°,∠C=80°,则∠DAE= °;
③试探究∠DAE与∠B、∠C的数量关系,并说明理由.
(2)判断与思考:如图②,F是AD上一点,FE⊥BC于点E,这时∠DFE与∠B、∠C又有怎样的数量关系?
15.如图,在△ABC中,∠B=31°,∠C=55°,AD⊥BC于D,AE平分∠BAC交BC于E,DF⊥AE于F,求∠ADF的度数.
16.如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠1和∠DAC的度数.
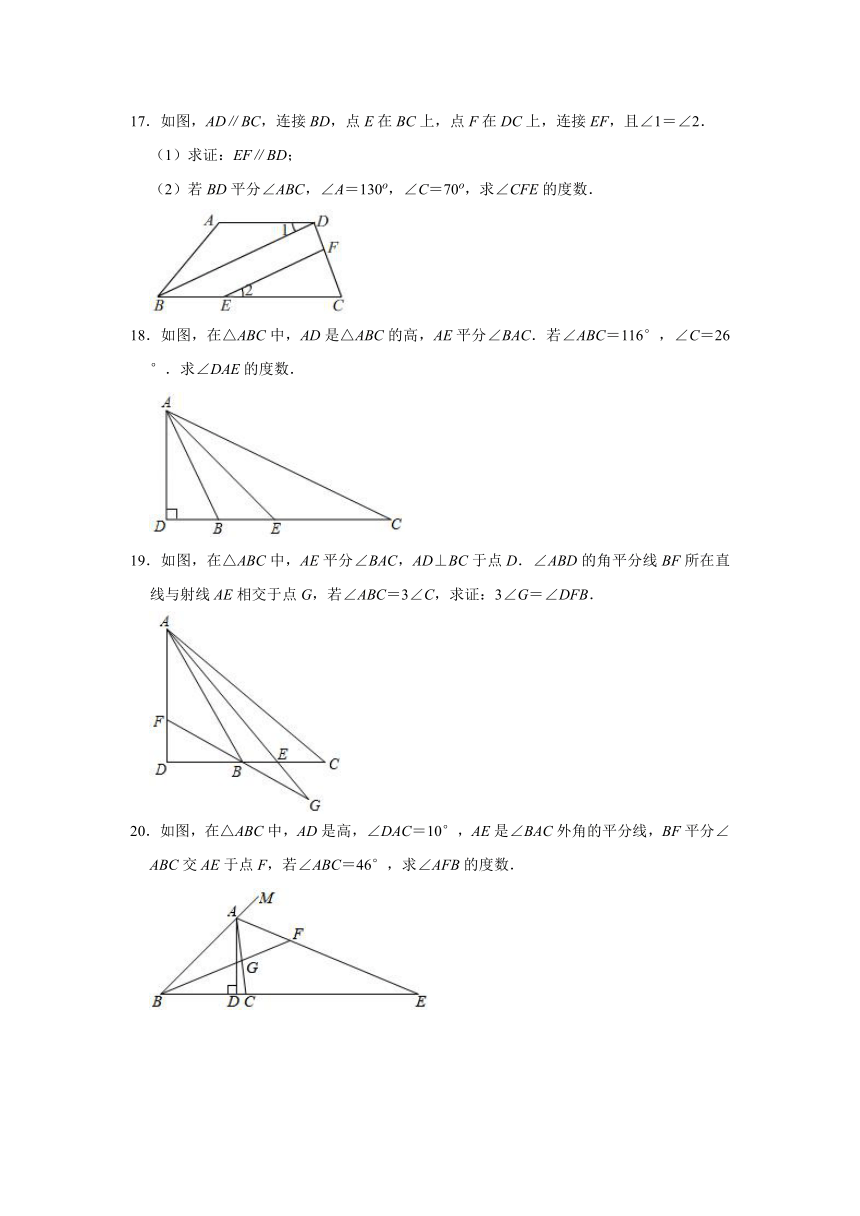
17.如图,AD∥BC,连接BD,点E在BC上,点F在DC上,连接EF,且∠1=∠2.
(1)求证:EF∥BD;
(2)若BD平分∠ABC,∠A=130o,∠C=70o,求∠CFE的度数.
18.如图,在△ABC中,AD是△ABC的高,AE平分∠BAC.若∠ABC=116°,∠C=26°.求∠DAE的度数.
19.如图,在△ABC中,AE平分∠BAC,AD⊥BC于点D.∠ABD的角平分线BF所在直线与射线AE相交于点G,若∠ABC=3∠C,求证:3∠G=∠DFB.
20.如图,在△ABC中,AD是高,∠DAC=10°,AE是∠BAC外角的平分线,BF平分∠ABC交AE于点F,若∠ABC=46°,求∠AFB的度数.
参考答案
1.解:∵∠1=∠A+∠ACB,∠2=∠A+∠ABC,
∴∠1+∠2=∠A+∠ACB+∠A+∠ABC=(∠A+∠ACB+∠ABC)+∠A.
又∵∠A+∠ABC+∠ACB=180°,∠A=50°,
∴∠1+∠2=180°+50°=230°.
故选:B.
2.解:由题意得:MN⊥PQ.
∴∠AOB=90°.
∴∠BAO+∠ABO=180°﹣∠AOB=180°﹣90°=90°.
又∵AE,BE分别是∠BAO和∠ABO的角平分线,
∴∠BAE=,∠ABE=.
∴∠BAE+∠ABE===×90°=45°.
∴∠AEB=180°﹣(∠BAE+∠ABE)=180°﹣45°=135°.
故选:B.
3.解:选项A:∵∠A=40°,∠B=50°,
∴∠C=180°﹣∠A﹣∠B=90°.
∴△ABC是直角三角形.
选项B:∵∠A=90°,
∴△ABC是直角三角形.
选项C:∵∠A+B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°.
∴∠C=90°.
∴△ABC是直角三角形.
选项D:∵∠A+∠B=2∠C,∠A+∠B+∠C=180°,
∴3∠C=180°.
∴∠C=60°.
∴∠A+∠B=120°.
∴无法确定△ABC是直角三角形.
故选:D.
4.解:∵∠AOB=125°,
∴∠OAB+∠OBA=55°,
∵AE,BF分别是∠BAC和∠ABC的角平分线,它们相交于点O,
∴∠BAC+∠ABC=2(∠OAB+∠OBA)=110°,
∴∠C=70°,
∵AD是BC边上的高,
∴∠ADC=90°,
∴∠CAD=20°,
即∠CAD的度数是20°.
故选:A.
5.解:∵三角形的两个内角度数分别为60°、50°,
∴这个三角形的第三个角为180°﹣60°﹣50°=70°,
∵最大的角70°是锐角,
∴这个三角形是锐角三角形.
故选:B.
6.解:∵EG∥BC,
∴∠CEG=∠ACB,
∵CD平分∠ACB,
∴∠ACB=2∠DCB,
∴∠CEG=2∠DCB,故①正确;
∵∠A=90°,
∴∠ACD+∠ADC=90°,
∵EG∥BC,且CG⊥EG于G,
∴∠CGE=∠GCB=90°,
∴∠GCD+∠BCD=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ADC=∠GCD,故②正确;
无法证明CA平分∠BCG,故③错误;
∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,
∴∠AEB+∠ADC=90°+(∠ABC+∠ACB)=135°,
∴∠DFE=360°﹣135°﹣90°=135°,
∴∠DFB=45°=∠CGE,故④正确;
所以其中正确的结论为①②④共3个,
故选:C.
7.解:∵∠DOC=∠AOB=90°,
∴∠DOC﹣∠BOC=∠AOB﹣∠COB,
即∠AOC=∠BOD,故②正确;
∵∠AOB=∠COD=90°,
∴∠COB+∠AOD=∠AOB+∠COD=180°,故④正确;
如图,AB与OC交于点P,
∵∠CPE=∠APO,∠C=45°,∠A=30°,∠CEA+∠CPE+∠C=∠AOC+∠APO+∠A=180°,
∴∠AOC﹣∠CEA=15°.故③正确;
没有条件能证明OE平分∠AOD,故①错误.
故选:D.
8.解:∵∠ACE是△ABC的外角,
∴∠A=∠ACE﹣∠ABC,
∵CD、BD分别平分∠ACE、∠ABC,
∴∠DCE=∠ACE,∠DBE=∠ABC,
∵∠DCE是△BCD的外角,
∴∠D=∠DCE﹣∠DBC=∠ACE﹣∠ABC=(∠ACE﹣∠ABC)===40°,
故选:B.
9.解:如图,
∵直线a∥b,
∴∠3=∠1,
∵∠1=56°,
∴∠3=56°,
∵∠3=∠2+∠A,∠2=29°,
∴∠A=∠3﹣∠2=56°﹣29°=27°.
故答案为:27.
10.解:∵AE⊥CD交CD于点F,
∴∠AFC=∠EFC=90°,
∵CD平分∠ACB,
∴∠ACF=∠ECF,
∵∠AFC+∠CAF+∠ACF=180°,∠EFC+∠CEA+∠ECF=180°,
∴∠CAF=∠CEA,
∵∠CEA=∠B+∠BAE,∠B=45°,∠BAE=20°,
∴∠CAE=65°,
∴∠CAF=65°,
故答案为:65°.
11.解:如图,
延长B'E,C'F,交于点D,
由折叠可得,∠B=∠B',∠C=∠C',
∴∠A=∠D,
又∵∠1+∠2=110°,
∴∠AED+∠AFD=360°﹣110°=250°,
∴四边形AEDF中,∠A=(360°﹣250°)=55°,
故答案为:55.
12.解:如图,由题意知,∠CAD=60°,∠B=90°﹣45°=45°,
∴∠CAB=120°,
∴∠1=∠B+∠CAB=45°+120°=165°.
故答案为:165°.
13.解:∵∠A=50°,
∴∠ABC+∠ACB=180°﹣50°=130°,
∵∠DBA=∠ABC,∠DCA=∠ACB,
∴∠DBA+∠DCA=(∠ABC+∠ACB)=26°,
∴∠DBC+∠DCB=130°﹣26°=104°,
∴∠D=180°﹣(∠DBC+∠DCB)=76°,故答案为:76°.
14.解:(1)探究与发现:
①在△ABC中,∠B+∠C+∠BAC=180°,∠B=20°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=90°,
∵AD是∠BAC角平分线,
∴∠CAD=∠BAC=×90°=45°,
∵AE⊥BC,
∴∠AEC=90°,
∴∠CAE=90°﹣70°=20°,
∴∠DAE=∠CAD﹣∠CAE=25°,
故答案为:45,25;
②∵∠B=40°,∠C=80°,
∴∠BAC=60°,
∵AD是∠BAC角平分线,
∴∠CAD=∠BAC=30°,
∵AE⊥BC,
∴∠AEC=90°,
∴∠CAE=90°﹣80°=10°,
∴∠DAE=∠CAD﹣∠CAE=20°,
故答案为:20;
③∠DAE=(∠C﹣∠B),理由如下:
在△AEC中,∠AEC+∠C+∠EAC=180°,
∴∠EAC=180°﹣∠AEC﹣∠C=180°﹣90°﹣∠C=90°﹣∠C,
∴∠DAE=∠CAD﹣∠EAC=×(180°﹣∠B﹣∠C)=(90°﹣∠B﹣∠C)﹣( 90°﹣∠C)=(∠C﹣∠B);
(2)判断与思考;∠DFE=(∠C﹣∠B),理由如下:
证明:∵AD平分∠BAC,
∴∠BAD==90°﹣(∠C+∠B),
∵∠ADC为△ABD的外角,
∴∠ADC=∠B+90°﹣(∠C+∠B)=90°+(∠B﹣∠C),
∵FE⊥BC,
∴∠FED=90°,
∴∠DFE=90°﹣[90°+(∠B﹣∠C)]=90°﹣90°﹣(∠B﹣∠C),
∴∠DFE=(∠C﹣∠B).
15.解:∵∠B=31°,∠C=55°,
∴∠BAC=94°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=47°,
∴∠AED=∠B+∠BAE=31°+47°=78°,
∵AD⊥BC,DF⊥AE,
∴∠EFD=∠ADE=90°,
∴∠AED+∠EDF=∠EDF+∠ADF,
∴∠ADF=∠AED=78°.
16.解:设∠1=∠2=x,则∠3=∠4=2x,
因为∠BAC=63°,
所以∠2+∠4=117°,即x+2x=117°,
所以x=39°,即∠1=39°,
所以∠3=∠4=78°,
∠DAC=180°﹣∠3﹣∠4=24°.
17.(1)证明:∵AD∥BC(已知),
∴∠1=∠CBD(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠CBD=∠2(等量代换),
∴EF∥BD(同位角相等,两直线平行).
(2)解:∵AD∥BC(已知),
∴∠A+∠ABC=180°,∠C+∠ADC=180°,(两直线平行,同旁内角互补),
∴∠ABC=180°﹣∠A=180°﹣130°=50°,
∠ADC=180°﹣∠C=180°﹣70°=110°,
∵BD平分∠ABC(已知),
∴∠CBD=∠ABC=×50°=25°(角平分线的定义),
∴∠1=∠CBD=25°,
∴∠BDC=∠ADC﹣∠1=110°﹣25°=85°,
∵EF∥BD,
∴∠CFE=∠BDC=85°(两直线平行,同位角相等).
18.解:∵AD是△ABC的高,
∴∠ADC=90°,
△ABC中,∠ABC=116°,∠C=26°,
∴∠BAC=180°﹣116°﹣26°=38°,
∵AE平分∠BAC,
∴∠EAC=∠BAC=19°,
△ADC中,∠DAC=90°﹣∠C=90°﹣26°=64°,
∴∠DAE=∠DAC﹣∠EAC=64°﹣19°=45°.
19.证明:∵AE平分∠BAC,BF平分∠ABD,
∴∠CAE=∠BAE,∠ABF=∠DBF,设∠CAE=∠BAE=x,
∵∠ABC=3∠C,
∴可以假设∠C=y,∠ABC=3y,
∴∠ABF=∠DBF=∠CBG=(180°﹣3y)=90°﹣y,
∵AD⊥CD,
∴∠D=90°,
∴∠DFB=90°﹣∠DBF=y,
设∠ABF=∠DBF=∠CBG=z,则,
∴∠G=y,
∴∠DFB=3∠G.
20.解:∵AD是高,
∴∠ADB=90°,
∴∠BAD=90°﹣∠ABC=44°,又∠DAC=10°,
∴∠BAC=54°,
∴∠MAC=126°,
∵AE是∠BAC外角的平分线,
∴∠MAE=∠MAC=63°,
∵BF平分∠ABC,
∴∠ABF=∠ABC=23°,
∴∠AFB=∠MAE﹣∠ABF=40°.
1.如图,在△ABC中,∠A=50°,则∠1+∠2的度数是( )
A.180° B.230° C.280° D.无法确定
2.直线MN与直线PQ垂直相交于O,点A在射线OP上运动,点B在射线OM上运动.如图,已知AE,BE分别是∠BAO和∠ABO的角平分线,点A,B在运动的过程中,∠AEB度数为( )
A.120° B.135° C.100° D.无法确定
3.已知∠A、∠B、∠C是△ABC的三个内角,下列条件不能确定△ABC是直角三角形的是( )
A.∠A=40°,∠B=50° B.∠A=90°
C.∠A+∠B=∠C D.∠A+∠B=2∠C
4.如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC和∠ABC的角平分线,它们相交于点O,∠AOB=125°,则∠CAD的度数为( )
A.20° B.30° C.45° D.50°
5.若一个三角形的两个内角的度数分别为60°,50°,则这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能确定
6.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB=∠CGE.
其中正确的结论的个数是( )
A.1 B.2 C.3 D.4
7.将一副学生用三角板(一个锐角为30°的直角三角形,一个锐角为45°的直角三角形)如图叠放,则下列4个结论中正确的个数有( )
①OE平分∠AOD;②∠AOC=∠BOD;③∠AOC﹣∠CEA=15°;
④∠COB+∠AOD=180°.
A.0 B.1 C.2 D.3
8.如图,CD、BD分别平分∠ACE、∠ABC,∠A=80°,则∠BDC=( )
A.35° B.40° C.30° D.45°
9.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=56°,∠2=29°,则∠A的度数为 度.
10.如图,在△ABC中,∠B=45°,CD平分∠ACB交AB于点D,过点A作AE⊥CD交BC于点E,交CD于点F,若∠BAE=20°,则∠CAF的大小为 .
11.如图△ABC中,将边BC沿虚线翻折,若∠1+∠2=110°,则∠A的度数是 度.
12.将一副直角三角板按如图放置,使两直角重合,则∠1的度数为 .
13.如图所示,在△ABC中,∠A=50°,点D在△ABC的内部,并且∠DBA=∠ABC,∠DCA=∠ACB,则∠D的度数是 .
14.综合与探究:
如图①,在△ABC中,∠C>∠B,AD是∠BAC角平分线.
(1)探究与发现:如图①,AE⊥BC于点E,
①若∠B=20°,∠C=70°,则∠CAD= °,∠DAE= °;
②若∠B=40°,∠C=80°,则∠DAE= °;
③试探究∠DAE与∠B、∠C的数量关系,并说明理由.
(2)判断与思考:如图②,F是AD上一点,FE⊥BC于点E,这时∠DFE与∠B、∠C又有怎样的数量关系?
15.如图,在△ABC中,∠B=31°,∠C=55°,AD⊥BC于D,AE平分∠BAC交BC于E,DF⊥AE于F,求∠ADF的度数.
16.如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠1和∠DAC的度数.
17.如图,AD∥BC,连接BD,点E在BC上,点F在DC上,连接EF,且∠1=∠2.
(1)求证:EF∥BD;
(2)若BD平分∠ABC,∠A=130o,∠C=70o,求∠CFE的度数.
18.如图,在△ABC中,AD是△ABC的高,AE平分∠BAC.若∠ABC=116°,∠C=26°.求∠DAE的度数.
19.如图,在△ABC中,AE平分∠BAC,AD⊥BC于点D.∠ABD的角平分线BF所在直线与射线AE相交于点G,若∠ABC=3∠C,求证:3∠G=∠DFB.
20.如图,在△ABC中,AD是高,∠DAC=10°,AE是∠BAC外角的平分线,BF平分∠ABC交AE于点F,若∠ABC=46°,求∠AFB的度数.
参考答案
1.解:∵∠1=∠A+∠ACB,∠2=∠A+∠ABC,
∴∠1+∠2=∠A+∠ACB+∠A+∠ABC=(∠A+∠ACB+∠ABC)+∠A.
又∵∠A+∠ABC+∠ACB=180°,∠A=50°,
∴∠1+∠2=180°+50°=230°.
故选:B.
2.解:由题意得:MN⊥PQ.
∴∠AOB=90°.
∴∠BAO+∠ABO=180°﹣∠AOB=180°﹣90°=90°.
又∵AE,BE分别是∠BAO和∠ABO的角平分线,
∴∠BAE=,∠ABE=.
∴∠BAE+∠ABE===×90°=45°.
∴∠AEB=180°﹣(∠BAE+∠ABE)=180°﹣45°=135°.
故选:B.
3.解:选项A:∵∠A=40°,∠B=50°,
∴∠C=180°﹣∠A﹣∠B=90°.
∴△ABC是直角三角形.
选项B:∵∠A=90°,
∴△ABC是直角三角形.
选项C:∵∠A+B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°.
∴∠C=90°.
∴△ABC是直角三角形.
选项D:∵∠A+∠B=2∠C,∠A+∠B+∠C=180°,
∴3∠C=180°.
∴∠C=60°.
∴∠A+∠B=120°.
∴无法确定△ABC是直角三角形.
故选:D.
4.解:∵∠AOB=125°,
∴∠OAB+∠OBA=55°,
∵AE,BF分别是∠BAC和∠ABC的角平分线,它们相交于点O,
∴∠BAC+∠ABC=2(∠OAB+∠OBA)=110°,
∴∠C=70°,
∵AD是BC边上的高,
∴∠ADC=90°,
∴∠CAD=20°,
即∠CAD的度数是20°.
故选:A.
5.解:∵三角形的两个内角度数分别为60°、50°,
∴这个三角形的第三个角为180°﹣60°﹣50°=70°,
∵最大的角70°是锐角,
∴这个三角形是锐角三角形.
故选:B.
6.解:∵EG∥BC,
∴∠CEG=∠ACB,
∵CD平分∠ACB,
∴∠ACB=2∠DCB,
∴∠CEG=2∠DCB,故①正确;
∵∠A=90°,
∴∠ACD+∠ADC=90°,
∵EG∥BC,且CG⊥EG于G,
∴∠CGE=∠GCB=90°,
∴∠GCD+∠BCD=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ADC=∠GCD,故②正确;
无法证明CA平分∠BCG,故③错误;
∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,
∴∠AEB+∠ADC=90°+(∠ABC+∠ACB)=135°,
∴∠DFE=360°﹣135°﹣90°=135°,
∴∠DFB=45°=∠CGE,故④正确;
所以其中正确的结论为①②④共3个,
故选:C.
7.解:∵∠DOC=∠AOB=90°,
∴∠DOC﹣∠BOC=∠AOB﹣∠COB,
即∠AOC=∠BOD,故②正确;
∵∠AOB=∠COD=90°,
∴∠COB+∠AOD=∠AOB+∠COD=180°,故④正确;
如图,AB与OC交于点P,
∵∠CPE=∠APO,∠C=45°,∠A=30°,∠CEA+∠CPE+∠C=∠AOC+∠APO+∠A=180°,
∴∠AOC﹣∠CEA=15°.故③正确;
没有条件能证明OE平分∠AOD,故①错误.
故选:D.
8.解:∵∠ACE是△ABC的外角,
∴∠A=∠ACE﹣∠ABC,
∵CD、BD分别平分∠ACE、∠ABC,
∴∠DCE=∠ACE,∠DBE=∠ABC,
∵∠DCE是△BCD的外角,
∴∠D=∠DCE﹣∠DBC=∠ACE﹣∠ABC=(∠ACE﹣∠ABC)===40°,
故选:B.
9.解:如图,
∵直线a∥b,
∴∠3=∠1,
∵∠1=56°,
∴∠3=56°,
∵∠3=∠2+∠A,∠2=29°,
∴∠A=∠3﹣∠2=56°﹣29°=27°.
故答案为:27.
10.解:∵AE⊥CD交CD于点F,
∴∠AFC=∠EFC=90°,
∵CD平分∠ACB,
∴∠ACF=∠ECF,
∵∠AFC+∠CAF+∠ACF=180°,∠EFC+∠CEA+∠ECF=180°,
∴∠CAF=∠CEA,
∵∠CEA=∠B+∠BAE,∠B=45°,∠BAE=20°,
∴∠CAE=65°,
∴∠CAF=65°,
故答案为:65°.
11.解:如图,
延长B'E,C'F,交于点D,
由折叠可得,∠B=∠B',∠C=∠C',
∴∠A=∠D,
又∵∠1+∠2=110°,
∴∠AED+∠AFD=360°﹣110°=250°,
∴四边形AEDF中,∠A=(360°﹣250°)=55°,
故答案为:55.
12.解:如图,由题意知,∠CAD=60°,∠B=90°﹣45°=45°,
∴∠CAB=120°,
∴∠1=∠B+∠CAB=45°+120°=165°.
故答案为:165°.
13.解:∵∠A=50°,
∴∠ABC+∠ACB=180°﹣50°=130°,
∵∠DBA=∠ABC,∠DCA=∠ACB,
∴∠DBA+∠DCA=(∠ABC+∠ACB)=26°,
∴∠DBC+∠DCB=130°﹣26°=104°,
∴∠D=180°﹣(∠DBC+∠DCB)=76°,故答案为:76°.
14.解:(1)探究与发现:
①在△ABC中,∠B+∠C+∠BAC=180°,∠B=20°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=90°,
∵AD是∠BAC角平分线,
∴∠CAD=∠BAC=×90°=45°,
∵AE⊥BC,
∴∠AEC=90°,
∴∠CAE=90°﹣70°=20°,
∴∠DAE=∠CAD﹣∠CAE=25°,
故答案为:45,25;
②∵∠B=40°,∠C=80°,
∴∠BAC=60°,
∵AD是∠BAC角平分线,
∴∠CAD=∠BAC=30°,
∵AE⊥BC,
∴∠AEC=90°,
∴∠CAE=90°﹣80°=10°,
∴∠DAE=∠CAD﹣∠CAE=20°,
故答案为:20;
③∠DAE=(∠C﹣∠B),理由如下:
在△AEC中,∠AEC+∠C+∠EAC=180°,
∴∠EAC=180°﹣∠AEC﹣∠C=180°﹣90°﹣∠C=90°﹣∠C,
∴∠DAE=∠CAD﹣∠EAC=×(180°﹣∠B﹣∠C)=(90°﹣∠B﹣∠C)﹣( 90°﹣∠C)=(∠C﹣∠B);
(2)判断与思考;∠DFE=(∠C﹣∠B),理由如下:
证明:∵AD平分∠BAC,
∴∠BAD==90°﹣(∠C+∠B),
∵∠ADC为△ABD的外角,
∴∠ADC=∠B+90°﹣(∠C+∠B)=90°+(∠B﹣∠C),
∵FE⊥BC,
∴∠FED=90°,
∴∠DFE=90°﹣[90°+(∠B﹣∠C)]=90°﹣90°﹣(∠B﹣∠C),
∴∠DFE=(∠C﹣∠B).
15.解:∵∠B=31°,∠C=55°,
∴∠BAC=94°,
∵AE平分∠BAC,
∴∠BAE=∠BAC=47°,
∴∠AED=∠B+∠BAE=31°+47°=78°,
∵AD⊥BC,DF⊥AE,
∴∠EFD=∠ADE=90°,
∴∠AED+∠EDF=∠EDF+∠ADF,
∴∠ADF=∠AED=78°.
16.解:设∠1=∠2=x,则∠3=∠4=2x,
因为∠BAC=63°,
所以∠2+∠4=117°,即x+2x=117°,
所以x=39°,即∠1=39°,
所以∠3=∠4=78°,
∠DAC=180°﹣∠3﹣∠4=24°.
17.(1)证明:∵AD∥BC(已知),
∴∠1=∠CBD(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠CBD=∠2(等量代换),
∴EF∥BD(同位角相等,两直线平行).
(2)解:∵AD∥BC(已知),
∴∠A+∠ABC=180°,∠C+∠ADC=180°,(两直线平行,同旁内角互补),
∴∠ABC=180°﹣∠A=180°﹣130°=50°,
∠ADC=180°﹣∠C=180°﹣70°=110°,
∵BD平分∠ABC(已知),
∴∠CBD=∠ABC=×50°=25°(角平分线的定义),
∴∠1=∠CBD=25°,
∴∠BDC=∠ADC﹣∠1=110°﹣25°=85°,
∵EF∥BD,
∴∠CFE=∠BDC=85°(两直线平行,同位角相等).
18.解:∵AD是△ABC的高,
∴∠ADC=90°,
△ABC中,∠ABC=116°,∠C=26°,
∴∠BAC=180°﹣116°﹣26°=38°,
∵AE平分∠BAC,
∴∠EAC=∠BAC=19°,
△ADC中,∠DAC=90°﹣∠C=90°﹣26°=64°,
∴∠DAE=∠DAC﹣∠EAC=64°﹣19°=45°.
19.证明:∵AE平分∠BAC,BF平分∠ABD,
∴∠CAE=∠BAE,∠ABF=∠DBF,设∠CAE=∠BAE=x,
∵∠ABC=3∠C,
∴可以假设∠C=y,∠ABC=3y,
∴∠ABF=∠DBF=∠CBG=(180°﹣3y)=90°﹣y,
∵AD⊥CD,
∴∠D=90°,
∴∠DFB=90°﹣∠DBF=y,
设∠ABF=∠DBF=∠CBG=z,则,
∴∠G=y,
∴∠DFB=3∠G.
20.解:∵AD是高,
∴∠ADB=90°,
∴∠BAD=90°﹣∠ABC=44°,又∠DAC=10°,
∴∠BAC=54°,
∴∠MAC=126°,
∵AE是∠BAC外角的平分线,
∴∠MAE=∠MAC=63°,
∵BF平分∠ABC,
∴∠ABF=∠ABC=23°,
∴∠AFB=∠MAE﹣∠ABF=40°.
