《11.3多边形及其内角和》同步能力提升训练(附答案)2021-2022学年八年级数学人教版上册
文档属性
| 名称 | 《11.3多边形及其内角和》同步能力提升训练(附答案)2021-2022学年八年级数学人教版上册 |
|
|
| 格式 | doc | ||
| 文件大小 | 245.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览

文档简介
2021年人教版八年级数学上册《11.3多边形及其内角和》同步能力提升训练(附答案)
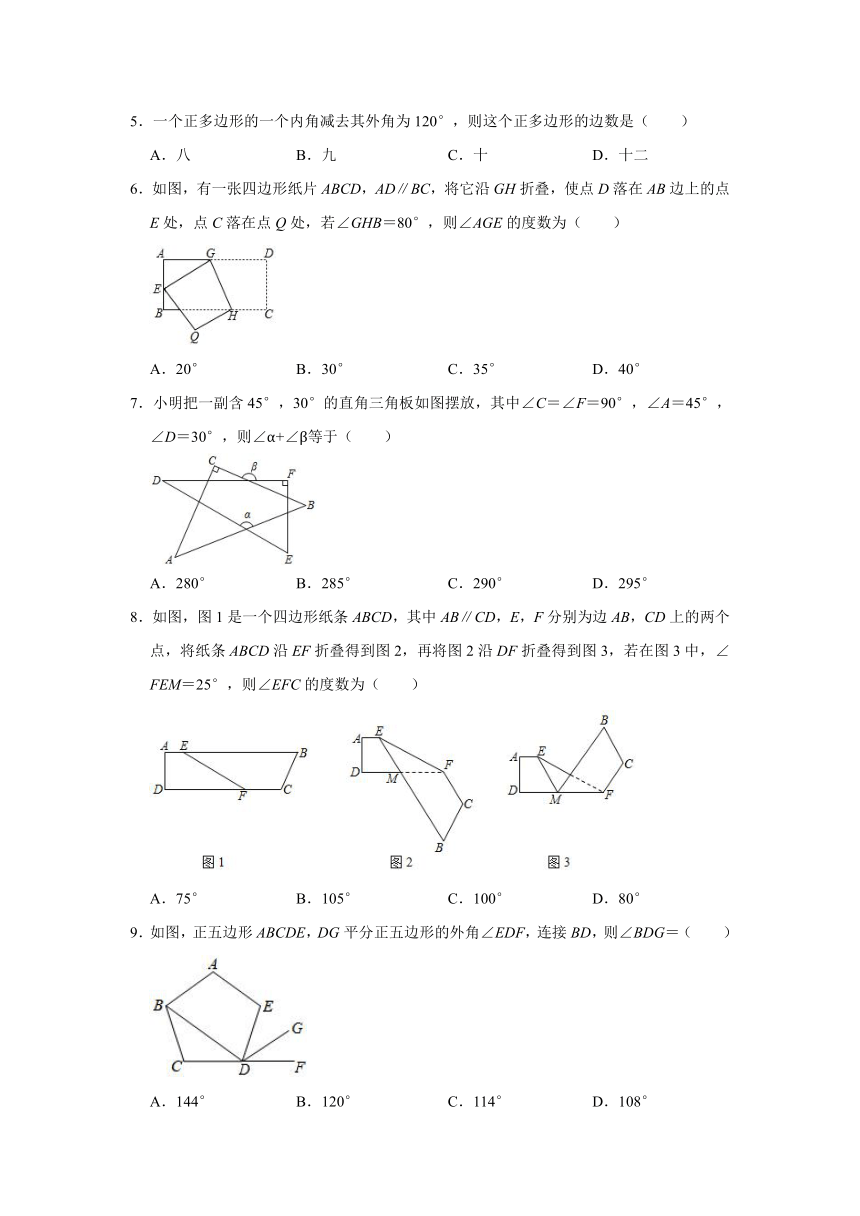
1.如图,把△ABC纸片沿DE折叠,当点C落在四边形ABDE的外部时,此时测得∠1=108°,∠C=35°,则∠2的度数为( )
A.35° B.36° C.37° D.38°
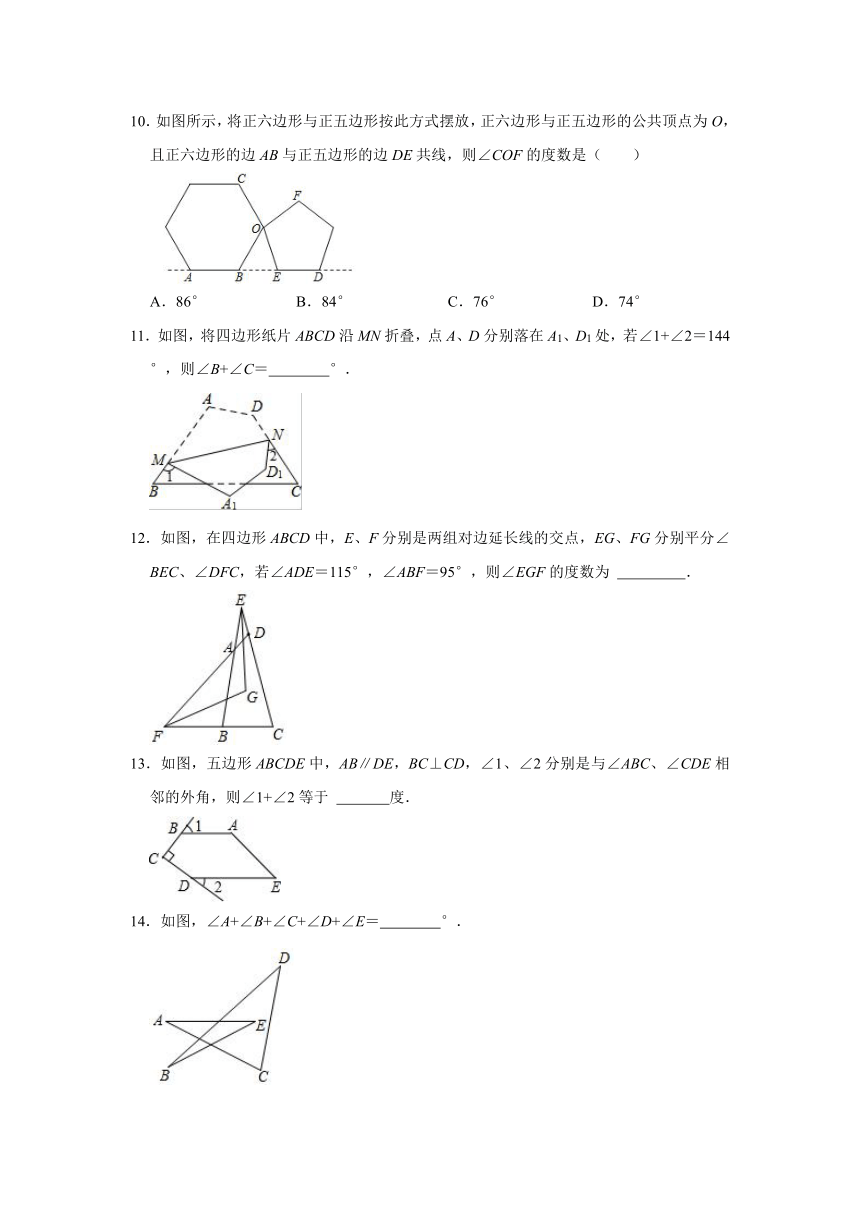
2.如图,四边形ABCD中,∠1、∠2、∠3分别为∠BAD、∠ABC、∠BCD的外角,下列判断正确的是( )
A.∠1+∠3=∠ABC+∠D B.∠1+∠3=180°
C.∠2=∠D D.∠1+∠2+∠3=360°
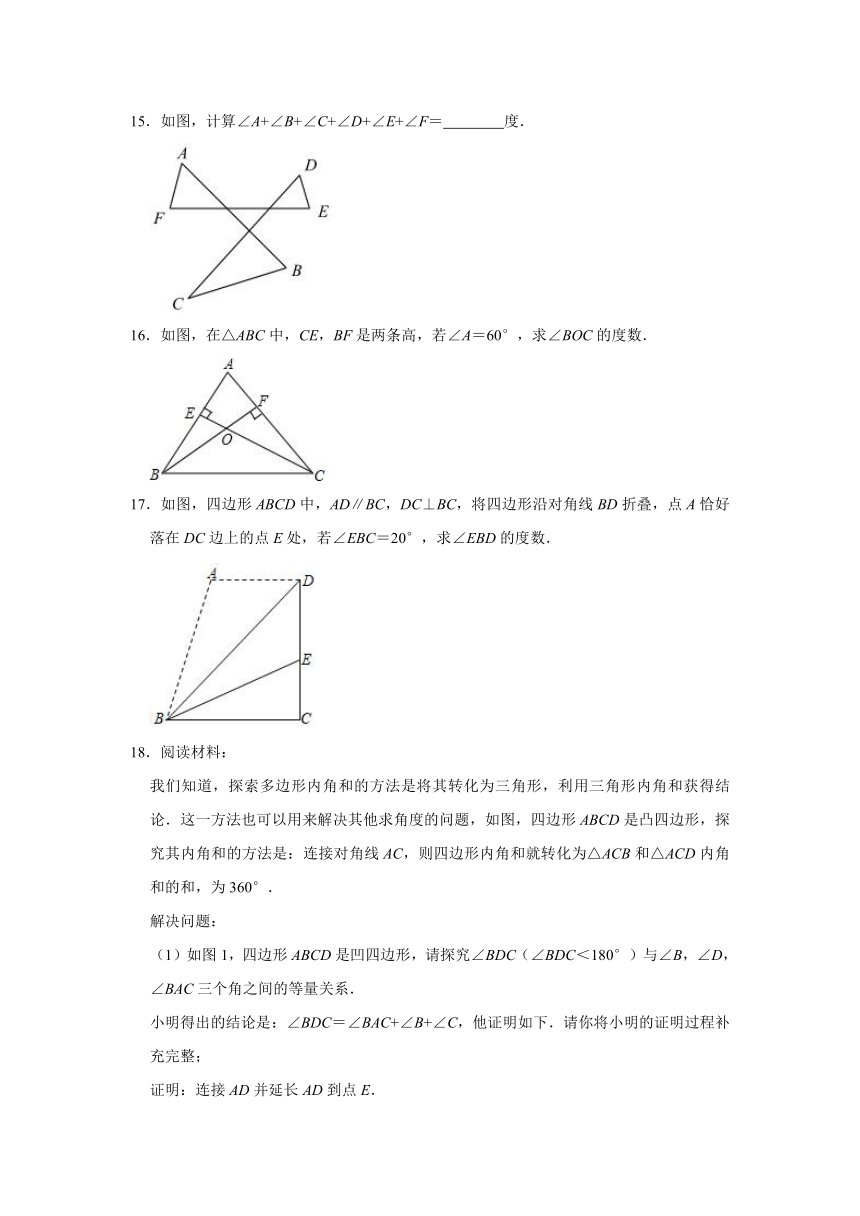
3.如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠FAI=( )
A.10° B.12° C.14° D.15°
4.如图,点A、B、C、D、E在同一平面内连接AB、BC、CD、DE、EA,若∠BCD=100°,则∠A+∠B+∠D+∠E=( )
A.220° B.240° C.260° D.280°
5.一个正多边形的一个内角减去其外角为120°,则这个正多边形的边数是( )
A.八 B.九 C.十 D.十二
6.如图,有一张四边形纸片ABCD,AD∥BC,将它沿GH折叠,使点D落在AB边上的点E处,点C落在点Q处,若∠GHB=80°,则∠AGE的度数为( )
A.20° B.30° C.35° D.40°
7.小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.280° B.285° C.290° D.295°
8.如图,图1是一个四边形纸条ABCD,其中AB∥CD,E,F分别为边AB,CD上的两个点,将纸条ABCD沿EF折叠得到图2,再将图2沿DF折叠得到图3,若在图3中,∠FEM=25°,则∠EFC的度数为( )
A.75° B.105° C.100° D.80°
9.如图,正五边形ABCDE,DG平分正五边形的外角∠EDF,连接BD,则∠BDG=( )
A.144° B.120° C.114° D.108°
10.如图所示,将正六边形与正五边形按此方式摆放,正六边形与正五边形的公共顶点为O,且正六边形的边AB与正五边形的边DE共线,则∠COF的度数是( )
A.86° B.84° C.76° D.74°
11.如图,将四边形纸片ABCD沿MN折叠,点A、D分别落在A1、D1处,若∠1+∠2=144°,则∠B+∠C= °.
12.如图,在四边形ABCD中,E、F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠DFC,若∠ADE=115°,∠ABF=95°,则∠EGF的度数为 .
13.如图,五边形ABCDE中,AB∥DE,BC⊥CD,∠1、∠2分别是与∠ABC、∠CDE相邻的外角,则∠1+∠2等于 度.
14.如图,∠A+∠B+∠C+∠D+∠E= °.
15.如图,计算∠A+∠B+∠C+∠D+∠E+∠F= 度.
16.如图,在△ABC中,CE,BF是两条高,若∠A=60°,求∠BOC的度数.
17.如图,四边形ABCD中,AD∥BC,DC⊥BC,将四边形沿对角线BD折叠,点A恰好落在DC边上的点E处,若∠EBC=20°,求∠EBD的度数.
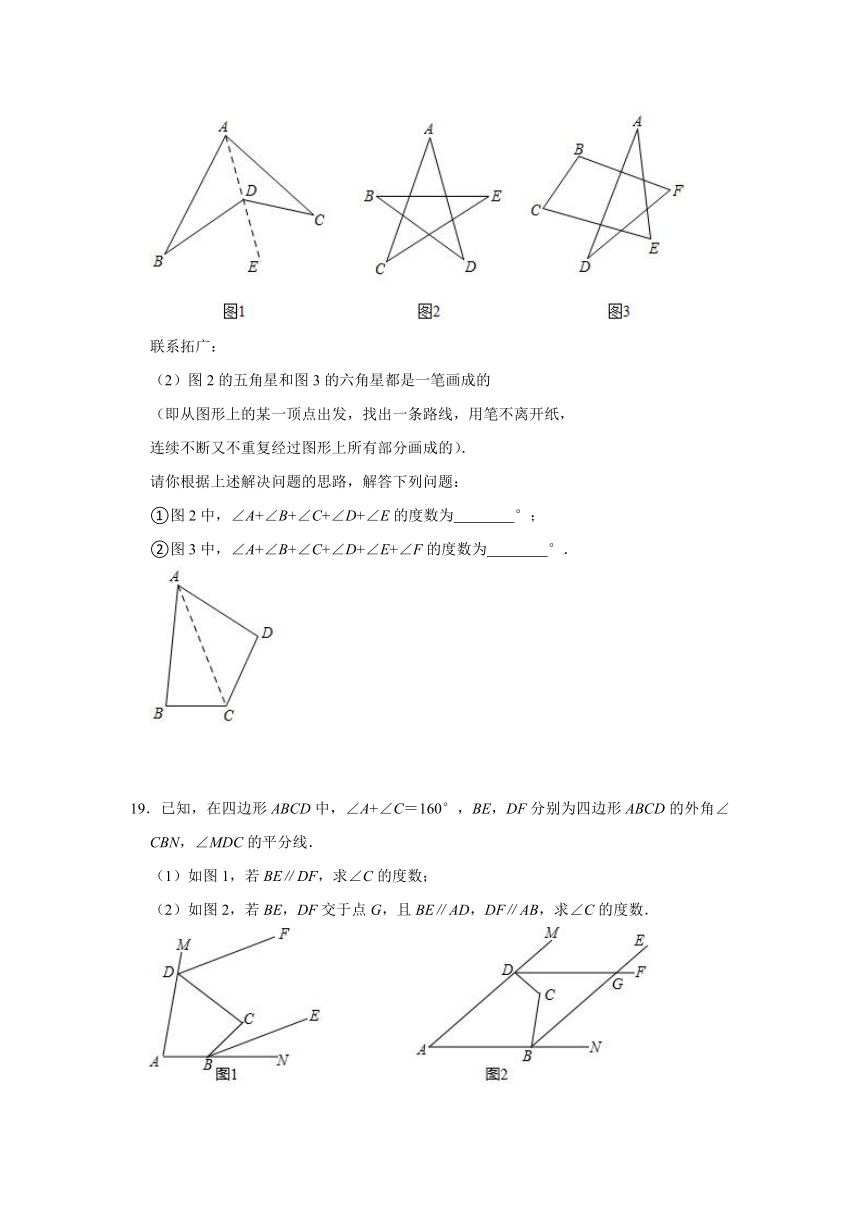
18.阅读材料:
我们知道,探索多边形内角和的方法是将其转化为三角形,利用三角形内角和获得结论.这一方法也可以用来解决其他求角度的问题,如图,四边形ABCD是凸四边形,探究其内角和的方法是:连接对角线AC,则四边形内角和就转化为△ACB和△ACD内角和的和,为360°.
解决问题:
(1)如图1,四边形ABCD是凹四边形,请探究∠BDC(∠BDC<180°)与∠B,∠D,∠BAC三个角之间的等量关系.
小明得出的结论是:∠BDC=∠BAC+∠B+∠C,他证明如下.请你将小明的证明过程补充完整;
证明:连接AD并延长AD到点E.
联系拓广:
(2)图2的五角星和图3的六角星都是一笔画成的
(即从图形上的某一顶点出发,找出一条路线,用笔不离开纸,
连续不断又不重复经过图形上所有部分画成的).
请你根据上述解决问题的思路,解答下列问题:
①图2中,∠A+∠B+∠C+∠D+∠E的度数为 °;
②图3中,∠A+∠B+∠C+∠D+∠E+∠F的度数为 °.
19.已知,在四边形ABCD中,∠A+∠C=160°,BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线.
(1)如图1,若BE∥DF,求∠C的度数;
(2)如图2,若BE,DF交于点G,且BE∥AD,DF∥AB,求∠C的度数.
20.四边形ABCD中,∠A=145°,∠D=75°.
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)①如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
②在①的条件下,若延长BA、CD交于点F(如图4),将原来条件“∠A=145°,∠D=75°”改为“∠F=40°”,其他条件不变,∠BEC的度数会发生变化吗?若不变,请说明理由;若变化,求出∠BEC的度数.
参考答案
1.解:如图,设C′D与AC交于点O,
∵∠C=35°,
∴∠C′=∠C=35°,
∵∠1=∠DOC+∠C,∠1=108°,
∴∠DOC=∠1﹣∠C=108°﹣35°=73°,
∵∠DOC=∠2+∠C′,
∴∠2=∠DOC﹣∠C′=73°﹣35°=38°.
故选:D.
2.解:∵∠1+∠DAB=180°,∠3+∠BCD=180°,
∴∠1+∠3+∠DAB+∠BCD=360°,
∵∠ABC+∠BCD+∠D+∠DAB=360°,
∴∠1+∠3=∠ABC+∠D,
故A符合题意;
∵∠1+∠3只有∠ABC和∠D互补时才等于180°,
故B不符合题意;
∵只有∠ABC和∠D互补时,∠2=∠D,
故C不符合题意;
∵多边形的外角和是360°,
∴∠1+∠2+∠3<360°,
故D不符合题意;
故选:A.
3.解:在正六边形ABCDEF内,正五边形ABGHI中,∠FAB=120°,∠IAB=108°,
∴∠FAI=∠FAB﹣∠IAB=120°﹣108°=12°,
故选:B.
4.解:连接BD,
∵∠BCD=100°,
∴∠CBD+∠CDB=180°﹣100°=80°,
∴∠A+∠ABC+∠E+∠CDE=360°﹣∠CBD﹣∠CDB=360°﹣80°=280°,
故选:D.
5.解:设内角为x°,则其外角为(x﹣120)°,由题意得:
x+(x﹣120)=180,
解得:x=150,
则其外角为150°﹣120°=30°,
这个正多边形的边数为:360°÷30°=12.
故选:D.
6.解:∵AD∥BC,∠GHB=80°,
∴∠DGH=∠GHB=80°,
由折叠的性质可得,∠EGH=∠DGH=80°,
∴∠AGE=180°﹣∠EGH﹣∠DGH=180°﹣80°﹣80°=20°.故选:A.
7.解:
∵∠C=∠F=90°,∠A=45°,∠D=30°,
∴∠2+∠3=180°﹣∠D=150°,
∵∠α=∠1+∠A,∠β=∠4+∠C,
∵∠1=∠2,∠3=∠4,
∴∠α+∠β=∠A+∠1+∠4+∠C=∠A+∠C+∠2+∠3=45°+90°+150°=285°,
故选:B.
8.解:如图②,由折叠得:∠B'EF=∠FEM=25°,
∵AE∥DF,
∴∠EFM=25°,∠BMF=∠DME=50°,
∵BM∥CF,
∴∠CFM+∠BMF=180°,
∴∠CFM=180°﹣50°=130°,
由折叠得:如图③,∠CFM=130°,
∴∠EFC=∠CFM﹣∠EFM=130°﹣25°=105°,
故选:B.
9.解:∵五边形ABCDE是正五边形,
∴∠EDF=360°÷5=72°,∠CDE=∠C=180°﹣72°=108°,BC=DC,
∴∠BDC==36°,
∴∠BDE=108°﹣∠BDC=108°﹣36°=72°,
∵DG平分正五边形的外角∠EDF,
∴∠EDG==36°,
∴∠BDG=∠BDE+∠EDG=72°+36°=108°,
故选:D.
10.解:由题意:∠EOF=108°,∠BOC=120°,∠OEB=72°,∠OBE=60°,
∴∠BOE=180°﹣72°﹣60°=48°,
∴∠COF=360°﹣108°﹣48°﹣120°=84°,
故选:B.
11.解:∵∠1+∠2=144°,
∴∠AMN+∠DNM==108°.
∵∠A+∠D+(∠AMN+∠DNM)=360°,∠A+∠D+(∠B+∠C)=360°,
∴∠B+∠C=∠AMN+∠DNM=108°.
故答案为:108.
12.解:如图:
连接EF,根据三角形内角和定理及角平分线的性质得:
∠EGF=180°﹣(∠GEF+∠GFE)=180°﹣(∠CEF﹣∠CEG+∠CFE﹣CFG)
=180°﹣(∠CEF+∠CFE)+(∠CFG+∠CEG)=∠C+∠CFD+∠CEB
=∠C+(180°﹣∠C﹣∠CDF)+(180°﹣∠C﹣∠CBE)
=∠C+180°﹣∠C﹣(180°﹣115°+180°﹣95°)=105°.
故答案为:105°.
13.解:连接BD,
∵BC⊥CD,
∴∠C=90°,
∴∠CBD+∠CDB=180°﹣90°=90°,
∵AB∥DE,
∴∠ABD+∠EDB=180°,
∴∠1+∠2=(180°﹣∠ABC)+(180°﹣∠EDC)=360°﹣(∠ABC+∠EDC)
=360°﹣(∠ABD+∠CBD+∠EDB+∠CDB)=360°﹣(90°+180°)=90°,
故答案为:90.
14.解:如图,设线段BD,BE分别与线段AC交于点N,M.
∵∠AMB=∠A+∠E,∠DNC=∠B+∠AMB,∠DNC+∠D+∠C=180°,
∴∠A+∠B+∠D+∠E+∠C=180°,
故答案为:180.
15.解:
∵∠1=∠A+∠F,∠2=∠D+∠E,∠3=∠B+∠C,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠1+∠2+∠3,
∠1、∠2、∠3是△MNP的三个不同外角,
∵∠1+∠2+∠3=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360.
16.解:∵BD⊥AC,
∴∠BDA=90°.
又∵∠A+BDA+∠ABD=180°,
∴∠ABD=180°﹣60°﹣90°=30°.
又∵CE⊥AB,
∴∠BEO=90°,
∴∠BOC=∠ABD+∠BEO=30°+90°=120°.
17.解:∵∠EBC=20°,DC⊥BC,
∴∠BEC=70°,
∴∠DEB=110°,
∴∠DAB=110°,
∵AD∥BC,
∴∠ABC=70°,
∴∠ABE=∠ABC﹣∠EBC=70°﹣20°=50°,
∴∠EBD=∠ABE=25°.
18.解:(1)证明:连接AD并延长AD到点E.
则∠BDE为△ABD的外角,∠CDE为△ACD的外角,
∴∠BDE=∠B+∠BAD,
∠CDE=∠C+∠CAD.
∵∠BDC=∠BDE+∠CDE,
∴∠BDC=∠B+∠BAD+∠C+∠CAD.
∵∠BAC=∠BAD+∠CAD,
∴∠BDC=∠B+∠C+∠BAC.
(2)①如图2,由(1)得,∠CFD=∠A+∠C+∠D,
∴∠BFE=∠CFD=∠A+∠C+∠D,
∵∠BFE+∠B+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
故答案为:180.
②如图3,由(1)得,∠DHE=∠A+∠D+∠E,
∴∠CHF=∠DHE=∠A+∠D+∠E,
∵∠F+∠B+∠C+∠CHF=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,
故答案为:360.
19.解:(1)如图1,过点C作CH∥DF,
∵BE∥DF,
∴BE∥DF∥CH,
∴∠FDC=∠DCH,∠BCH=∠EBC,
∴∠DCB=∠DCH+∠BCH=∠FDC+∠EBC,
∵BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线,
∴∠FDC=∠CDM,∠EBC=,
∵∠A+∠BCD=160°,
∴∠ADC+∠ABC=360°﹣160°=200°,
∴∠MDC+∠CBN=160°,
∴∠FDC+∠CBE=80°,
∴∠DCB=80°;
(2)如图2,连接GC并延长,
同理得∠MDC+∠CBN=160°,∠MDF+∠NBG=80°,
∵BE∥AD,DF∥AB,
∴∠A=∠MDF=∠DGB=∠NBG=40°,
∵∠A+∠BCD=160°,
∴∠BCD=160°﹣40°=120°.
20.解:(1)∵四边形ABCD中,∠A=145°,∠D=75°,
∴∠B+∠C=360°﹣(145°+75°)=140°,
∵∠B=∠C,
∴∠C=70°;
(2)∵BE∥AD,
∴∠ABE=180°﹣∠A=180°﹣145°=35°,
∵∠ABC的角平分线BE交DC于点E,
∴∠ABC=70°,
∴∠C=360°﹣(145°+75°+70°)=70°;
(3)①∵四边形ABCD中,∠A=145°,∠D=75°,
∴∠B+∠C=360°﹣(145°+75°)=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°﹣70°=110°;
②不变.
∵∠F=40°,
∴∠FBC+∠BCF=180°﹣40°=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°﹣70°=110°.
1.如图,把△ABC纸片沿DE折叠,当点C落在四边形ABDE的外部时,此时测得∠1=108°,∠C=35°,则∠2的度数为( )
A.35° B.36° C.37° D.38°
2.如图,四边形ABCD中,∠1、∠2、∠3分别为∠BAD、∠ABC、∠BCD的外角,下列判断正确的是( )
A.∠1+∠3=∠ABC+∠D B.∠1+∠3=180°
C.∠2=∠D D.∠1+∠2+∠3=360°
3.如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠FAI=( )
A.10° B.12° C.14° D.15°
4.如图,点A、B、C、D、E在同一平面内连接AB、BC、CD、DE、EA,若∠BCD=100°,则∠A+∠B+∠D+∠E=( )
A.220° B.240° C.260° D.280°
5.一个正多边形的一个内角减去其外角为120°,则这个正多边形的边数是( )
A.八 B.九 C.十 D.十二
6.如图,有一张四边形纸片ABCD,AD∥BC,将它沿GH折叠,使点D落在AB边上的点E处,点C落在点Q处,若∠GHB=80°,则∠AGE的度数为( )
A.20° B.30° C.35° D.40°
7.小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.280° B.285° C.290° D.295°
8.如图,图1是一个四边形纸条ABCD,其中AB∥CD,E,F分别为边AB,CD上的两个点,将纸条ABCD沿EF折叠得到图2,再将图2沿DF折叠得到图3,若在图3中,∠FEM=25°,则∠EFC的度数为( )
A.75° B.105° C.100° D.80°
9.如图,正五边形ABCDE,DG平分正五边形的外角∠EDF,连接BD,则∠BDG=( )
A.144° B.120° C.114° D.108°
10.如图所示,将正六边形与正五边形按此方式摆放,正六边形与正五边形的公共顶点为O,且正六边形的边AB与正五边形的边DE共线,则∠COF的度数是( )
A.86° B.84° C.76° D.74°
11.如图,将四边形纸片ABCD沿MN折叠,点A、D分别落在A1、D1处,若∠1+∠2=144°,则∠B+∠C= °.
12.如图,在四边形ABCD中,E、F分别是两组对边延长线的交点,EG、FG分别平分∠BEC、∠DFC,若∠ADE=115°,∠ABF=95°,则∠EGF的度数为 .
13.如图,五边形ABCDE中,AB∥DE,BC⊥CD,∠1、∠2分别是与∠ABC、∠CDE相邻的外角,则∠1+∠2等于 度.
14.如图,∠A+∠B+∠C+∠D+∠E= °.
15.如图,计算∠A+∠B+∠C+∠D+∠E+∠F= 度.
16.如图,在△ABC中,CE,BF是两条高,若∠A=60°,求∠BOC的度数.
17.如图,四边形ABCD中,AD∥BC,DC⊥BC,将四边形沿对角线BD折叠,点A恰好落在DC边上的点E处,若∠EBC=20°,求∠EBD的度数.
18.阅读材料:
我们知道,探索多边形内角和的方法是将其转化为三角形,利用三角形内角和获得结论.这一方法也可以用来解决其他求角度的问题,如图,四边形ABCD是凸四边形,探究其内角和的方法是:连接对角线AC,则四边形内角和就转化为△ACB和△ACD内角和的和,为360°.
解决问题:
(1)如图1,四边形ABCD是凹四边形,请探究∠BDC(∠BDC<180°)与∠B,∠D,∠BAC三个角之间的等量关系.
小明得出的结论是:∠BDC=∠BAC+∠B+∠C,他证明如下.请你将小明的证明过程补充完整;
证明:连接AD并延长AD到点E.
联系拓广:
(2)图2的五角星和图3的六角星都是一笔画成的
(即从图形上的某一顶点出发,找出一条路线,用笔不离开纸,
连续不断又不重复经过图形上所有部分画成的).
请你根据上述解决问题的思路,解答下列问题:
①图2中,∠A+∠B+∠C+∠D+∠E的度数为 °;
②图3中,∠A+∠B+∠C+∠D+∠E+∠F的度数为 °.
19.已知,在四边形ABCD中,∠A+∠C=160°,BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线.
(1)如图1,若BE∥DF,求∠C的度数;
(2)如图2,若BE,DF交于点G,且BE∥AD,DF∥AB,求∠C的度数.
20.四边形ABCD中,∠A=145°,∠D=75°.
(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数;
(3)①如图3,若∠ABC和∠BCD的角平分线交于点E,试求出∠BEC的度数.
②在①的条件下,若延长BA、CD交于点F(如图4),将原来条件“∠A=145°,∠D=75°”改为“∠F=40°”,其他条件不变,∠BEC的度数会发生变化吗?若不变,请说明理由;若变化,求出∠BEC的度数.
参考答案
1.解:如图,设C′D与AC交于点O,
∵∠C=35°,
∴∠C′=∠C=35°,
∵∠1=∠DOC+∠C,∠1=108°,
∴∠DOC=∠1﹣∠C=108°﹣35°=73°,
∵∠DOC=∠2+∠C′,
∴∠2=∠DOC﹣∠C′=73°﹣35°=38°.
故选:D.
2.解:∵∠1+∠DAB=180°,∠3+∠BCD=180°,
∴∠1+∠3+∠DAB+∠BCD=360°,
∵∠ABC+∠BCD+∠D+∠DAB=360°,
∴∠1+∠3=∠ABC+∠D,
故A符合题意;
∵∠1+∠3只有∠ABC和∠D互补时才等于180°,
故B不符合题意;
∵只有∠ABC和∠D互补时,∠2=∠D,
故C不符合题意;
∵多边形的外角和是360°,
∴∠1+∠2+∠3<360°,
故D不符合题意;
故选:A.
3.解:在正六边形ABCDEF内,正五边形ABGHI中,∠FAB=120°,∠IAB=108°,
∴∠FAI=∠FAB﹣∠IAB=120°﹣108°=12°,
故选:B.
4.解:连接BD,
∵∠BCD=100°,
∴∠CBD+∠CDB=180°﹣100°=80°,
∴∠A+∠ABC+∠E+∠CDE=360°﹣∠CBD﹣∠CDB=360°﹣80°=280°,
故选:D.
5.解:设内角为x°,则其外角为(x﹣120)°,由题意得:
x+(x﹣120)=180,
解得:x=150,
则其外角为150°﹣120°=30°,
这个正多边形的边数为:360°÷30°=12.
故选:D.
6.解:∵AD∥BC,∠GHB=80°,
∴∠DGH=∠GHB=80°,
由折叠的性质可得,∠EGH=∠DGH=80°,
∴∠AGE=180°﹣∠EGH﹣∠DGH=180°﹣80°﹣80°=20°.故选:A.
7.解:
∵∠C=∠F=90°,∠A=45°,∠D=30°,
∴∠2+∠3=180°﹣∠D=150°,
∵∠α=∠1+∠A,∠β=∠4+∠C,
∵∠1=∠2,∠3=∠4,
∴∠α+∠β=∠A+∠1+∠4+∠C=∠A+∠C+∠2+∠3=45°+90°+150°=285°,
故选:B.
8.解:如图②,由折叠得:∠B'EF=∠FEM=25°,
∵AE∥DF,
∴∠EFM=25°,∠BMF=∠DME=50°,
∵BM∥CF,
∴∠CFM+∠BMF=180°,
∴∠CFM=180°﹣50°=130°,
由折叠得:如图③,∠CFM=130°,
∴∠EFC=∠CFM﹣∠EFM=130°﹣25°=105°,
故选:B.
9.解:∵五边形ABCDE是正五边形,
∴∠EDF=360°÷5=72°,∠CDE=∠C=180°﹣72°=108°,BC=DC,
∴∠BDC==36°,
∴∠BDE=108°﹣∠BDC=108°﹣36°=72°,
∵DG平分正五边形的外角∠EDF,
∴∠EDG==36°,
∴∠BDG=∠BDE+∠EDG=72°+36°=108°,
故选:D.
10.解:由题意:∠EOF=108°,∠BOC=120°,∠OEB=72°,∠OBE=60°,
∴∠BOE=180°﹣72°﹣60°=48°,
∴∠COF=360°﹣108°﹣48°﹣120°=84°,
故选:B.
11.解:∵∠1+∠2=144°,
∴∠AMN+∠DNM==108°.
∵∠A+∠D+(∠AMN+∠DNM)=360°,∠A+∠D+(∠B+∠C)=360°,
∴∠B+∠C=∠AMN+∠DNM=108°.
故答案为:108.
12.解:如图:
连接EF,根据三角形内角和定理及角平分线的性质得:
∠EGF=180°﹣(∠GEF+∠GFE)=180°﹣(∠CEF﹣∠CEG+∠CFE﹣CFG)
=180°﹣(∠CEF+∠CFE)+(∠CFG+∠CEG)=∠C+∠CFD+∠CEB
=∠C+(180°﹣∠C﹣∠CDF)+(180°﹣∠C﹣∠CBE)
=∠C+180°﹣∠C﹣(180°﹣115°+180°﹣95°)=105°.
故答案为:105°.
13.解:连接BD,
∵BC⊥CD,
∴∠C=90°,
∴∠CBD+∠CDB=180°﹣90°=90°,
∵AB∥DE,
∴∠ABD+∠EDB=180°,
∴∠1+∠2=(180°﹣∠ABC)+(180°﹣∠EDC)=360°﹣(∠ABC+∠EDC)
=360°﹣(∠ABD+∠CBD+∠EDB+∠CDB)=360°﹣(90°+180°)=90°,
故答案为:90.
14.解:如图,设线段BD,BE分别与线段AC交于点N,M.
∵∠AMB=∠A+∠E,∠DNC=∠B+∠AMB,∠DNC+∠D+∠C=180°,
∴∠A+∠B+∠D+∠E+∠C=180°,
故答案为:180.
15.解:
∵∠1=∠A+∠F,∠2=∠D+∠E,∠3=∠B+∠C,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠1+∠2+∠3,
∠1、∠2、∠3是△MNP的三个不同外角,
∵∠1+∠2+∠3=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360.
16.解:∵BD⊥AC,
∴∠BDA=90°.
又∵∠A+BDA+∠ABD=180°,
∴∠ABD=180°﹣60°﹣90°=30°.
又∵CE⊥AB,
∴∠BEO=90°,
∴∠BOC=∠ABD+∠BEO=30°+90°=120°.
17.解:∵∠EBC=20°,DC⊥BC,
∴∠BEC=70°,
∴∠DEB=110°,
∴∠DAB=110°,
∵AD∥BC,
∴∠ABC=70°,
∴∠ABE=∠ABC﹣∠EBC=70°﹣20°=50°,
∴∠EBD=∠ABE=25°.
18.解:(1)证明:连接AD并延长AD到点E.
则∠BDE为△ABD的外角,∠CDE为△ACD的外角,
∴∠BDE=∠B+∠BAD,
∠CDE=∠C+∠CAD.
∵∠BDC=∠BDE+∠CDE,
∴∠BDC=∠B+∠BAD+∠C+∠CAD.
∵∠BAC=∠BAD+∠CAD,
∴∠BDC=∠B+∠C+∠BAC.
(2)①如图2,由(1)得,∠CFD=∠A+∠C+∠D,
∴∠BFE=∠CFD=∠A+∠C+∠D,
∵∠BFE+∠B+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
故答案为:180.
②如图3,由(1)得,∠DHE=∠A+∠D+∠E,
∴∠CHF=∠DHE=∠A+∠D+∠E,
∵∠F+∠B+∠C+∠CHF=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,
故答案为:360.
19.解:(1)如图1,过点C作CH∥DF,
∵BE∥DF,
∴BE∥DF∥CH,
∴∠FDC=∠DCH,∠BCH=∠EBC,
∴∠DCB=∠DCH+∠BCH=∠FDC+∠EBC,
∵BE,DF分别为四边形ABCD的外角∠CBN,∠MDC的平分线,
∴∠FDC=∠CDM,∠EBC=,
∵∠A+∠BCD=160°,
∴∠ADC+∠ABC=360°﹣160°=200°,
∴∠MDC+∠CBN=160°,
∴∠FDC+∠CBE=80°,
∴∠DCB=80°;
(2)如图2,连接GC并延长,
同理得∠MDC+∠CBN=160°,∠MDF+∠NBG=80°,
∵BE∥AD,DF∥AB,
∴∠A=∠MDF=∠DGB=∠NBG=40°,
∵∠A+∠BCD=160°,
∴∠BCD=160°﹣40°=120°.
20.解:(1)∵四边形ABCD中,∠A=145°,∠D=75°,
∴∠B+∠C=360°﹣(145°+75°)=140°,
∵∠B=∠C,
∴∠C=70°;
(2)∵BE∥AD,
∴∠ABE=180°﹣∠A=180°﹣145°=35°,
∵∠ABC的角平分线BE交DC于点E,
∴∠ABC=70°,
∴∠C=360°﹣(145°+75°+70°)=70°;
(3)①∵四边形ABCD中,∠A=145°,∠D=75°,
∴∠B+∠C=360°﹣(145°+75°)=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°﹣70°=110°;
②不变.
∵∠F=40°,
∴∠FBC+∠BCF=180°﹣40°=140°,
∵∠ABC和∠BCD的角平分线交于点E,
∴∠EBC+∠ECB=70°,
∴∠BEC=180°﹣70°=110°.
