《13.2 画轴对称图形》同步习题 2020-2021学年数学人教版八年级上册(Word版 附答案)
文档属性
| 名称 | 《13.2 画轴对称图形》同步习题 2020-2021学年数学人教版八年级上册(Word版 附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览



文档简介
《13.2 画轴对称图形》同步习题2020-2021年数学人教新版八(上)
一.选择题(共17小题)
1.如果点,,和点关于轴对称,则的值是
A. B.1 C. D.5
2.在平面直角坐标系中,若点与点关于轴对称,则的值是
A.1 B.2 C.3 D.4
3.若点关于轴的对称点在第四象限,则的取值范围在数轴上表示为
A.
B.
C.
D.
4.在平面直角坐标系中,点与点关于轴对称,则
A., B., C., D.,
5.在平面直角坐标系中,将点向右平移5个单位长度得到点,则点关于轴对称点的坐标为
A. B. C. D.
6.在平面直角坐标系中,将点向右平移2个单位长度得到点,则点关于轴的对称点的坐标为
A. B. C. D.
7.若点与点关于轴对称,则点所在象限为
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.点和关于轴对称,则的值为
A. B.1 C. D.
9.如图,在平面直角坐标系中,对进行循环往复的轴对称变换,若原来点坐标是,则经过第2021次变换后点的对应点的坐标为
A. B. C. D.
10.已知点与点关于某条直线对称,则这条直线是
A.轴
B.轴
C.过点且垂直于轴的直线
D.过点且平行于轴的直线
11.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用表示,右下角方子的位置用表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是
A. B. C. D.
12.若点,在第二象限,则点关于直线(直线上各点的横坐标都是对称的点坐标是
A. B. C. D.
13.平面直角坐标系中,已知点在第四象限,则点关于直线对称的点的坐标是
A. B. C. D.
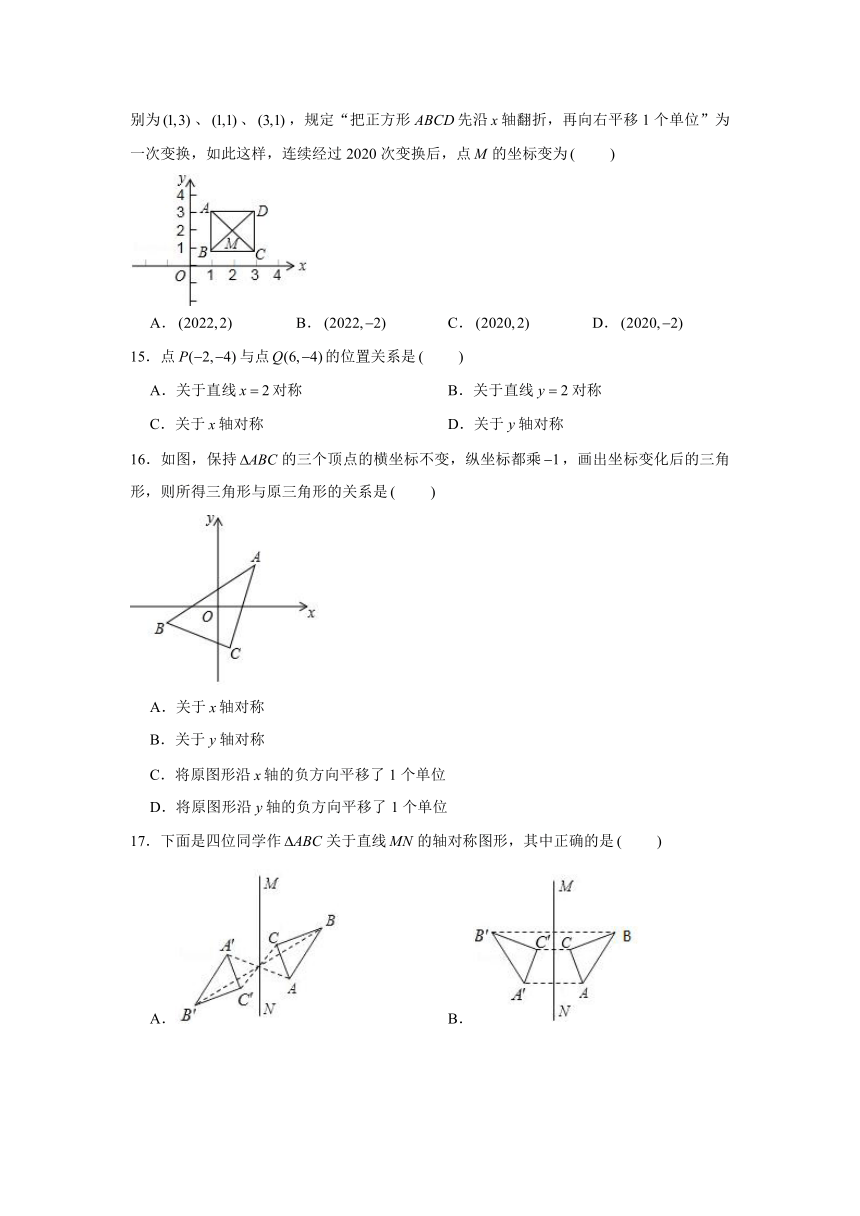
14.如图,已知正方形的对角线,相交于点,顶点、、的坐标分别为、、,规定“把正方形先沿轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2020次变换后,点的坐标变为
A. B. C. D.
15.点与点的位置关系是
A.关于直线对称 B.关于直线对称
C.关于轴对称 D.关于轴对称
16.如图,保持的三个顶点的横坐标不变,纵坐标都乘,画出坐标变化后的三角形,则所得三角形与原三角形的关系是
A.关于轴对称
B.关于轴对称
C.将原图形沿轴的负方向平移了1个单位
D.将原图形沿轴的负方向平移了1个单位
17.下面是四位同学作关于直线的轴对称图形,其中正确的是
A. B.
C. D.
二.填空题(共2小题)
18.在平面直角坐标系中,若点和关于轴对称,则 .
19.平面直角坐标系中,先作出点关于轴的对称点,再将该对称点先向下平移1个单位,再向左平移2个单位得到点,称为完成一次图形变换,再将点进行同样的图形变换得到点,依此类推,则点的坐标为 .
三.解答题(共11小题)
20.在的正方形网格中建立如图1、2所示的直角坐标系,其中格点,的坐标分别是,.(1)请图1中添加一个格点,使得是轴对称图形,且对称轴经过点.
(2)请图2中添加一个格点,使得也是轴对称图形,且对称轴经过点.
21.如图,已知的三个顶点的坐标分别为、、.
(1)将向右平移五个单位,再向下平移四个单位,则平移后点的对应点的坐标是 .
(2)将沿轴翻折,则翻折后点的对应点的坐标是 .
(3)求点关于直线(即第一、第三象限的角平分线)的对称点的坐标;请画图并说明理由.
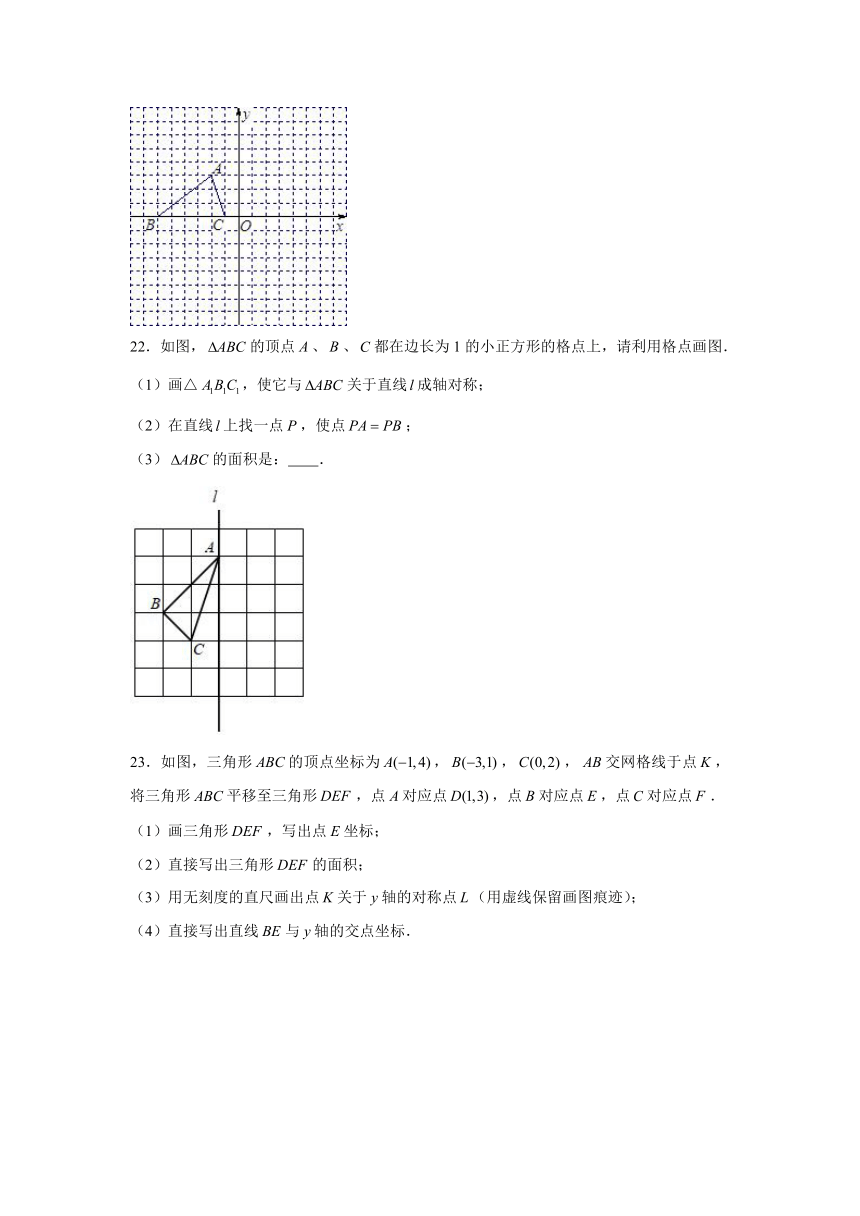
22.如图,的顶点、、都在边长为1的小正方形的格点上,请利用格点画图.
(1)画△,使它与关于直线成轴对称;
(2)在直线上找一点,使点;
(3)的面积是: .
23.如图,三角形的顶点坐标为,,,交网格线于点,将三角形平移至三角形,点对应点,点对应点,点对应点.
(1)画三角形,写出点坐标;
(2)直接写出三角形的面积;
(3)用无刻度的直尺画出点关于轴的对称点(用虚线保留画图痕迹);
(4)直接写出直线与轴的交点坐标.
24.如图,在平面直角坐标系中,的三个顶点分别为,,,直线为第一、第三象限的角平分线.
(1)请作出关于直线对称的图形△、、的对称点分别是、、;(保留作图痕迹)
(2)点的坐标是 .
25.在的方格纸中,的三个顶点都在格点上.在图中画出与成轴对称的格点三角形(画出4个即可).
26.如图,在平面直角坐标系中,直线是第一、三象限的角平分线.
由图观察易知点,、.
(1)若点、、关于直线的对称点分别为,请直接在图中画出△;
(2)坐标平面内任一点关于第一、三象限的角平分线的对称点的坐标为 .
27.已知在平面直角坐标系中,如图所示,,,.
(1)作出关于轴对称的图形△;
(2)求出的面积;
(3)在边上找一点,连接,使得.(请仅用无刻度直尺按要求画图)
(温馨提示:请把图画在相对应的图上,并且在图上标上字母.
28.已知:如图,,点在射线上,点,在射线上(点在点的右侧),且.点关于直线的对称点为,连接.
(1)依题意补全图形;
(2)猜想线段,的数量关系,并证明.
29.在中,,,分别是边上的两点,,点关于直线的对称点是点,连接,;
(1)如图1,当时;
①依题意补全图形;
②若,则 ;(用含的式子表示)
③求证:;
(2)如图2,当时,依题意补全图形,用等式表示线段,,之间的数量关系,并证明.
30.如图,在数学活动课中,小明剪了一张的纸片,其中,他将折叠压平使点落在点处,折痕,在上,在上.
(1)请作出折痕;(要求:尺规作图,不写作法,保留作图痕迹)
(2)判断的形状并说明;
(3)若,的周长为12,求的周长.
参考答案
一.选择题(共17小题)
1.解:点,,和点关于轴对称,
,,
则.
故选:.
2.解:点与点关于轴对称,
,,
,,
则.
故选:.
3.解:点关于轴的对称点在第四象限,
点在第一象限,
,
解得:,
在数轴上表示为:,
故选:.
4.解:点与点关于轴对称,
,,
解得:,
故选:.
5.解:点向右平移5个单位长度得到的的坐标为,即,
则点关于轴的对称点的坐标是:.
故选:.
6.解:将点向右平移2个单位长度得到点,
则点关于轴的对称点的坐标为.
故选:.
7.解:点与点关于轴对称,
,
解得:
则点所在象限为第一象限.
故选:.
8.解:点和关于轴对称,
且,
解得:,,
,
故选:.
9.解:点第一次关于轴对称后在第二象限,
点第二次关于轴对称后在第三象限,
点第三次关于轴对称后在第四象限,
点第四次关于轴对称后在第一象限,即点回到原始位置,
所以,每四次对称为一个循环组依次循环,
余1,
经过第2021次变换后所得的点与第一次变换的位置相同,在第二象限,坐标为.
故选:.
10.解:点与点的位置关系是关于直线对称,
故选:.
11.解:如图:小莹放的位置所表示的点的坐标是.
故选:.
12.解:直线上各点的横坐标都是1,
直线为:,
点在第二象限,
到1的距离为:,
点关于直线对称的点的横坐标是:,
故点对称的点的坐标是:.
故选:.
13.解:设关于直线的对称点为,
则有,
,
,
故选:.
14.解:正方形,顶点,,,
对角线交点的坐标为,
根据题意得:第1次变换后的点的对应点的坐标为,即,
第2次变换后的点的对应点的坐标为:,即,
第3次变换后的点的对应点的坐标为,即,
第次变换后的点的对应点的坐标为:当为奇数时为,当为偶数时为,
连续经过2020次变换后,正方形的对角线交点的坐标变为.
故选:.
15.解:点与点的位置关系是关于直线对称,
故选:.
16.解:纵坐标乘以,
变化前后纵坐标互为相反数,
又横坐标不变,
所得三角形与原三角形关于轴对称.
故选:.
17.解:作关于直线的轴对称图形正确的是选项,
故选:.
二.填空题(共2小题)
18.解:点和关于轴对称,
,
解得:,
则.
故答案为:.
19.解:如图,观察图像可知,偶数点在直线上,奇数点在轴上.
由题意,
,
,
,
故答案为:.
三.解答题(共11小题)
20.解:(1)如图,点即为所求.
(2)如图,点即为所求.
21.解:(1)平移后点的对应点的横坐标为,纵坐标为,故答案为;
(2)翻折后点的对应点的横坐标为,纵坐标为,
故答案为;
(3)由图中可以看出点的坐标为.
22.解:(1)如图,△为所作;
(2)如图,点为所作;
(3)的面积.
故答案为2.
23.解:(1)如图,三角形即为所求,点坐标
(2)三角形的面积.
(3)如图,点即为所求.
(4)如图,直线与轴的交点.
24.解:(1)如图,△即为所求作.
(2).
故答案为:.
25.解:如图所示,、、△、即为所求.
26.解:(1)如图,△即为所求作.
(2)坐标平面内任一点关于第一、三象限的角平分线的对称点的坐标为.
故答案为:.
27.解:(1)如图,△为所作;
(2)的面积;
(3)如图,点为所作.
28.解:(1)如图所示:
(2)猜想:.
证明:连接,,
点关于直线的对称点为,点在射线上,
,,
,
,即,
在中,,
又,
,
,
,
又,
是等边三角形,
,
.
29.解:(1)①如图,
②,
,
,
.
故答案为:.
③,关于对称,
,
,
,
,
,
,
是等边三角形,
.
(2)线段,,之间的数量关系:.
理由:如图.
,,
,
,关于对称,
,
,
,
同法可证,,
,
是等腰直角三角形,
,
.
30.解:(1)根据题意得:
作的垂直平分线,垂足为,交于,即为所求,
如图所示:
(2)是等边三角形,理由如下:
如图所示:
是的垂直平分线,
,
,
是等边三角形;
(3)的周长为12,
,
,
,
是等边三角形,
,
的周长.
一.选择题(共17小题)
1.如果点,,和点关于轴对称,则的值是
A. B.1 C. D.5
2.在平面直角坐标系中,若点与点关于轴对称,则的值是
A.1 B.2 C.3 D.4
3.若点关于轴的对称点在第四象限,则的取值范围在数轴上表示为
A.
B.
C.
D.
4.在平面直角坐标系中,点与点关于轴对称,则
A., B., C., D.,
5.在平面直角坐标系中,将点向右平移5个单位长度得到点,则点关于轴对称点的坐标为
A. B. C. D.
6.在平面直角坐标系中,将点向右平移2个单位长度得到点,则点关于轴的对称点的坐标为
A. B. C. D.
7.若点与点关于轴对称,则点所在象限为
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.点和关于轴对称,则的值为
A. B.1 C. D.
9.如图,在平面直角坐标系中,对进行循环往复的轴对称变换,若原来点坐标是,则经过第2021次变换后点的对应点的坐标为
A. B. C. D.
10.已知点与点关于某条直线对称,则这条直线是
A.轴
B.轴
C.过点且垂直于轴的直线
D.过点且平行于轴的直线
11.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用表示,右下角方子的位置用表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.她放的位置是
A. B. C. D.
12.若点,在第二象限,则点关于直线(直线上各点的横坐标都是对称的点坐标是
A. B. C. D.
13.平面直角坐标系中,已知点在第四象限,则点关于直线对称的点的坐标是
A. B. C. D.
14.如图,已知正方形的对角线,相交于点,顶点、、的坐标分别为、、,规定“把正方形先沿轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2020次变换后,点的坐标变为
A. B. C. D.
15.点与点的位置关系是
A.关于直线对称 B.关于直线对称
C.关于轴对称 D.关于轴对称
16.如图,保持的三个顶点的横坐标不变,纵坐标都乘,画出坐标变化后的三角形,则所得三角形与原三角形的关系是
A.关于轴对称
B.关于轴对称
C.将原图形沿轴的负方向平移了1个单位
D.将原图形沿轴的负方向平移了1个单位
17.下面是四位同学作关于直线的轴对称图形,其中正确的是
A. B.
C. D.
二.填空题(共2小题)
18.在平面直角坐标系中,若点和关于轴对称,则 .
19.平面直角坐标系中,先作出点关于轴的对称点,再将该对称点先向下平移1个单位,再向左平移2个单位得到点,称为完成一次图形变换,再将点进行同样的图形变换得到点,依此类推,则点的坐标为 .
三.解答题(共11小题)
20.在的正方形网格中建立如图1、2所示的直角坐标系,其中格点,的坐标分别是,.(1)请图1中添加一个格点,使得是轴对称图形,且对称轴经过点.
(2)请图2中添加一个格点,使得也是轴对称图形,且对称轴经过点.
21.如图,已知的三个顶点的坐标分别为、、.
(1)将向右平移五个单位,再向下平移四个单位,则平移后点的对应点的坐标是 .
(2)将沿轴翻折,则翻折后点的对应点的坐标是 .
(3)求点关于直线(即第一、第三象限的角平分线)的对称点的坐标;请画图并说明理由.
22.如图,的顶点、、都在边长为1的小正方形的格点上,请利用格点画图.
(1)画△,使它与关于直线成轴对称;
(2)在直线上找一点,使点;
(3)的面积是: .
23.如图,三角形的顶点坐标为,,,交网格线于点,将三角形平移至三角形,点对应点,点对应点,点对应点.
(1)画三角形,写出点坐标;
(2)直接写出三角形的面积;
(3)用无刻度的直尺画出点关于轴的对称点(用虚线保留画图痕迹);
(4)直接写出直线与轴的交点坐标.
24.如图,在平面直角坐标系中,的三个顶点分别为,,,直线为第一、第三象限的角平分线.
(1)请作出关于直线对称的图形△、、的对称点分别是、、;(保留作图痕迹)
(2)点的坐标是 .
25.在的方格纸中,的三个顶点都在格点上.在图中画出与成轴对称的格点三角形(画出4个即可).
26.如图,在平面直角坐标系中,直线是第一、三象限的角平分线.
由图观察易知点,、.
(1)若点、、关于直线的对称点分别为,请直接在图中画出△;
(2)坐标平面内任一点关于第一、三象限的角平分线的对称点的坐标为 .
27.已知在平面直角坐标系中,如图所示,,,.
(1)作出关于轴对称的图形△;
(2)求出的面积;
(3)在边上找一点,连接,使得.(请仅用无刻度直尺按要求画图)
(温馨提示:请把图画在相对应的图上,并且在图上标上字母.
28.已知:如图,,点在射线上,点,在射线上(点在点的右侧),且.点关于直线的对称点为,连接.
(1)依题意补全图形;
(2)猜想线段,的数量关系,并证明.
29.在中,,,分别是边上的两点,,点关于直线的对称点是点,连接,;
(1)如图1,当时;
①依题意补全图形;
②若,则 ;(用含的式子表示)
③求证:;
(2)如图2,当时,依题意补全图形,用等式表示线段,,之间的数量关系,并证明.
30.如图,在数学活动课中,小明剪了一张的纸片,其中,他将折叠压平使点落在点处,折痕,在上,在上.
(1)请作出折痕;(要求:尺规作图,不写作法,保留作图痕迹)
(2)判断的形状并说明;
(3)若,的周长为12,求的周长.
参考答案
一.选择题(共17小题)
1.解:点,,和点关于轴对称,
,,
则.
故选:.
2.解:点与点关于轴对称,
,,
,,
则.
故选:.
3.解:点关于轴的对称点在第四象限,
点在第一象限,
,
解得:,
在数轴上表示为:,
故选:.
4.解:点与点关于轴对称,
,,
解得:,
故选:.
5.解:点向右平移5个单位长度得到的的坐标为,即,
则点关于轴的对称点的坐标是:.
故选:.
6.解:将点向右平移2个单位长度得到点,
则点关于轴的对称点的坐标为.
故选:.
7.解:点与点关于轴对称,
,
解得:
则点所在象限为第一象限.
故选:.
8.解:点和关于轴对称,
且,
解得:,,
,
故选:.
9.解:点第一次关于轴对称后在第二象限,
点第二次关于轴对称后在第三象限,
点第三次关于轴对称后在第四象限,
点第四次关于轴对称后在第一象限,即点回到原始位置,
所以,每四次对称为一个循环组依次循环,
余1,
经过第2021次变换后所得的点与第一次变换的位置相同,在第二象限,坐标为.
故选:.
10.解:点与点的位置关系是关于直线对称,
故选:.
11.解:如图:小莹放的位置所表示的点的坐标是.
故选:.
12.解:直线上各点的横坐标都是1,
直线为:,
点在第二象限,
到1的距离为:,
点关于直线对称的点的横坐标是:,
故点对称的点的坐标是:.
故选:.
13.解:设关于直线的对称点为,
则有,
,
,
故选:.
14.解:正方形,顶点,,,
对角线交点的坐标为,
根据题意得:第1次变换后的点的对应点的坐标为,即,
第2次变换后的点的对应点的坐标为:,即,
第3次变换后的点的对应点的坐标为,即,
第次变换后的点的对应点的坐标为:当为奇数时为,当为偶数时为,
连续经过2020次变换后,正方形的对角线交点的坐标变为.
故选:.
15.解:点与点的位置关系是关于直线对称,
故选:.
16.解:纵坐标乘以,
变化前后纵坐标互为相反数,
又横坐标不变,
所得三角形与原三角形关于轴对称.
故选:.
17.解:作关于直线的轴对称图形正确的是选项,
故选:.
二.填空题(共2小题)
18.解:点和关于轴对称,
,
解得:,
则.
故答案为:.
19.解:如图,观察图像可知,偶数点在直线上,奇数点在轴上.
由题意,
,
,
,
故答案为:.
三.解答题(共11小题)
20.解:(1)如图,点即为所求.
(2)如图,点即为所求.
21.解:(1)平移后点的对应点的横坐标为,纵坐标为,故答案为;
(2)翻折后点的对应点的横坐标为,纵坐标为,
故答案为;
(3)由图中可以看出点的坐标为.
22.解:(1)如图,△为所作;
(2)如图,点为所作;
(3)的面积.
故答案为2.
23.解:(1)如图,三角形即为所求,点坐标
(2)三角形的面积.
(3)如图,点即为所求.
(4)如图,直线与轴的交点.
24.解:(1)如图,△即为所求作.
(2).
故答案为:.
25.解:如图所示,、、△、即为所求.
26.解:(1)如图,△即为所求作.
(2)坐标平面内任一点关于第一、三象限的角平分线的对称点的坐标为.
故答案为:.
27.解:(1)如图,△为所作;
(2)的面积;
(3)如图,点为所作.
28.解:(1)如图所示:
(2)猜想:.
证明:连接,,
点关于直线的对称点为,点在射线上,
,,
,
,即,
在中,,
又,
,
,
,
又,
是等边三角形,
,
.
29.解:(1)①如图,
②,
,
,
.
故答案为:.
③,关于对称,
,
,
,
,
,
,
是等边三角形,
.
(2)线段,,之间的数量关系:.
理由:如图.
,,
,
,关于对称,
,
,
,
同法可证,,
,
是等腰直角三角形,
,
.
30.解:(1)根据题意得:
作的垂直平分线,垂足为,交于,即为所求,
如图所示:
(2)是等边三角形,理由如下:
如图所示:
是的垂直平分线,
,
,
是等边三角形;
(3)的周长为12,
,
,
,
是等边三角形,
,
的周长.
