2021—2022学年人教版八年级数学上册11.2与三角形有关的角 同步专题优生辅导训练 (word版有答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学上册11.2与三角形有关的角 同步专题优生辅导训练 (word版有答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 277.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览


文档简介
2021年人教版八年级数学上册《11.2与三角形有关的角》同步专题优生辅导训练(附答案)
1.已知∠A、∠B、∠C是△ABC的三个内角,下列条件不能确定△ABC是直角三角形的是( )
A.∠A=40°,∠B=50° B.∠A=90°
C.∠A+∠B=∠C D.∠A+∠B=2∠C
2.在△ABC中,如果∠A:∠B:∠C=1:2:3,那么△ABC的形状是( )
A.直角三角形 B.锐角三角形
C.等腰三角形 D.等腰直角三角形
3.如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC和∠ABC的角平分线,它们相交于点O,∠AOB=125°,则∠CAD的度数为( )
A.20° B.30° C.45° D.50°
4.将一副三角板按如图方式重叠,则∠1的度数为( )
A.45° B.60° C.75° D.105°
5.下列说法中,正确的是( )
A.三角形的高都在三角形内 B.三角形的三条中线相交于三角形内一点
C.三角形的一个外角大于任何一个内角 D.三角形最大的一个内角的度数可以小于60度
6.如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是( )
A.30° B.40° C.50° D.60°
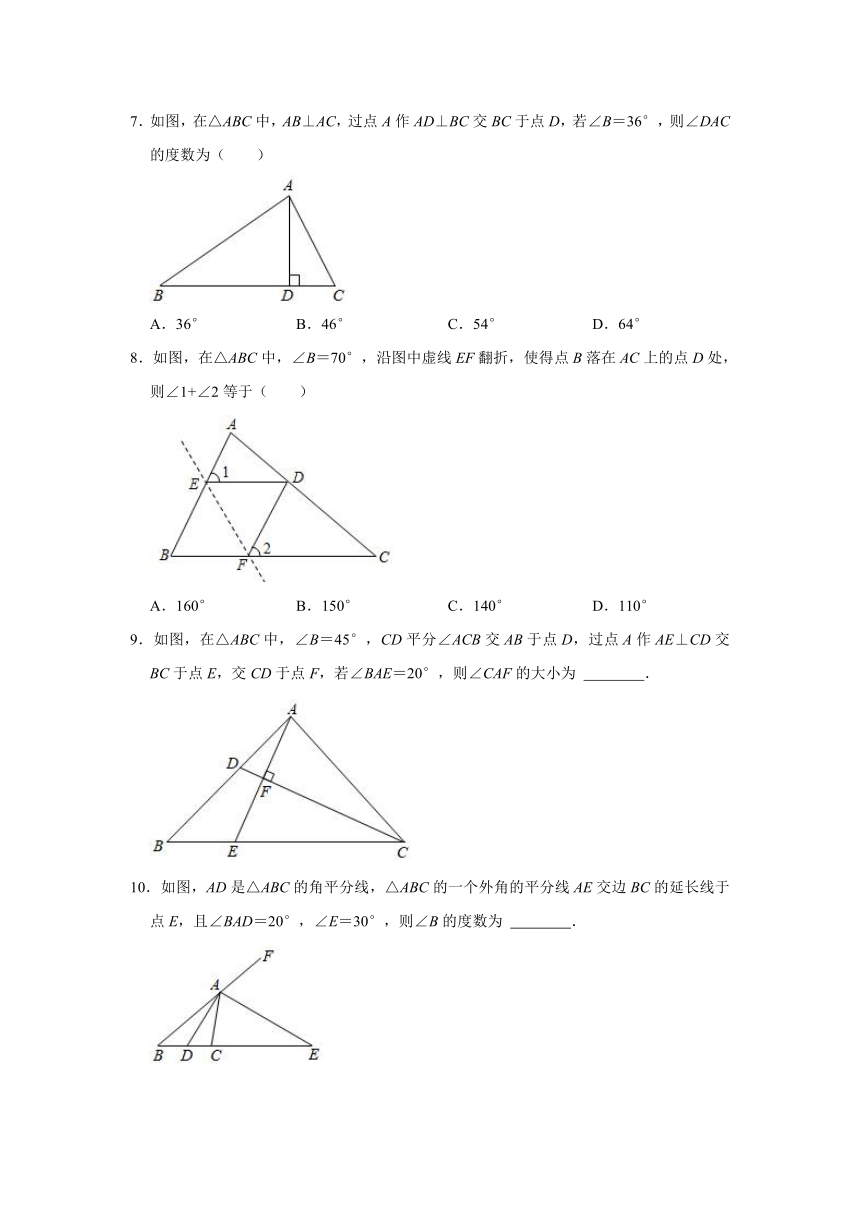
7.如图,在△ABC中,AB⊥AC,过点A作AD⊥BC交BC于点D,若∠B=36°,则∠DAC的度数为( )
A.36° B.46° C.54° D.64°
8.如图,在△ABC中,∠B=70°,沿图中虚线EF翻折,使得点B落在AC上的点D处,则∠1+∠2等于( )
A.160° B.150° C.140° D.110°
9.如图,在△ABC中,∠B=45°,CD平分∠ACB交AB于点D,过点A作AE⊥CD交BC于点E,交CD于点F,若∠BAE=20°,则∠CAF的大小为 .
10.如图,AD是△ABC的角平分线,△ABC的一个外角的平分线AE交边BC的延长线于点E,且∠BAD=20°,∠E=30°,则∠B的度数为 .
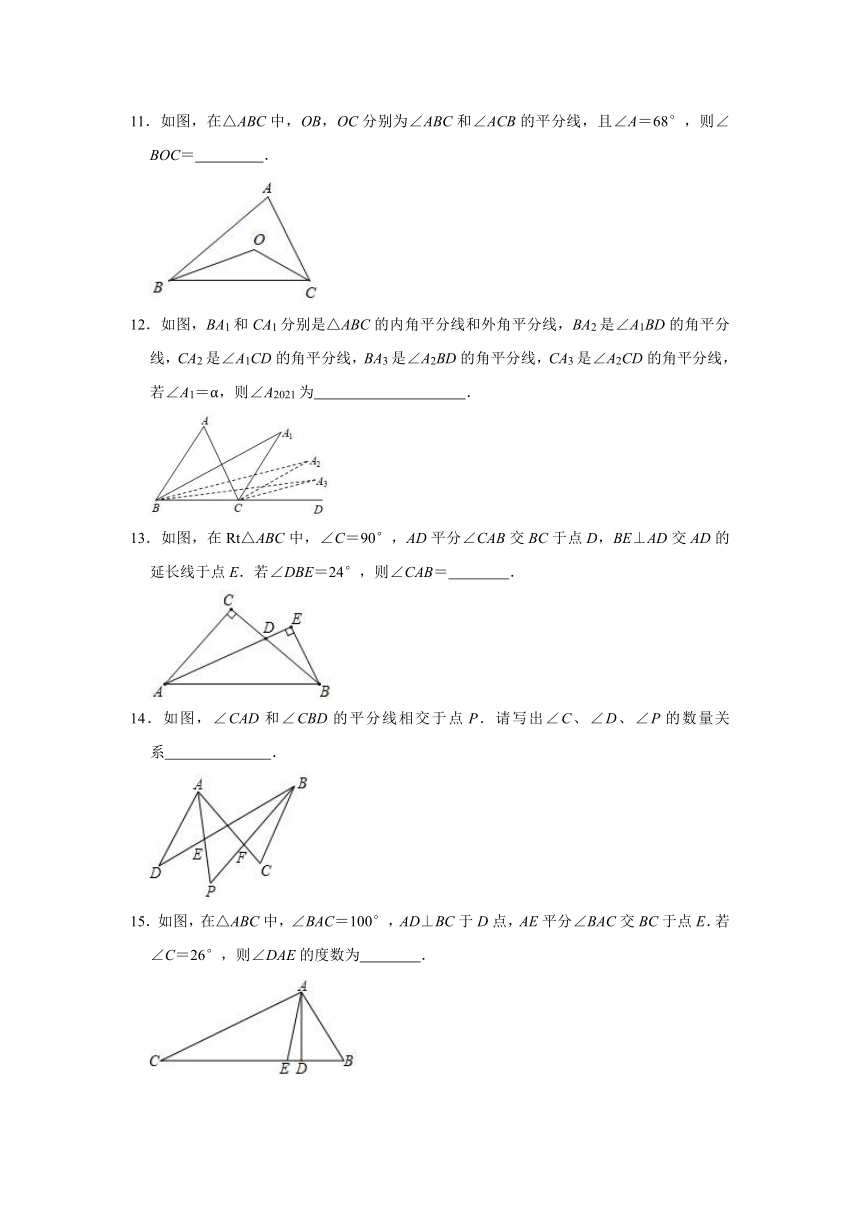
11.如图,在△ABC中,OB,OC分别为∠ABC和∠ACB的平分线,且∠A=68°,则∠BOC= .
12.如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2021为 .
13.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,BE⊥AD交AD的延长线于点E.若∠DBE=24°,则∠CAB= .
14.如图,∠CAD和∠CBD的平分线相交于点P.请写出∠C、∠D、∠P的数量关系 .
15.如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为 .
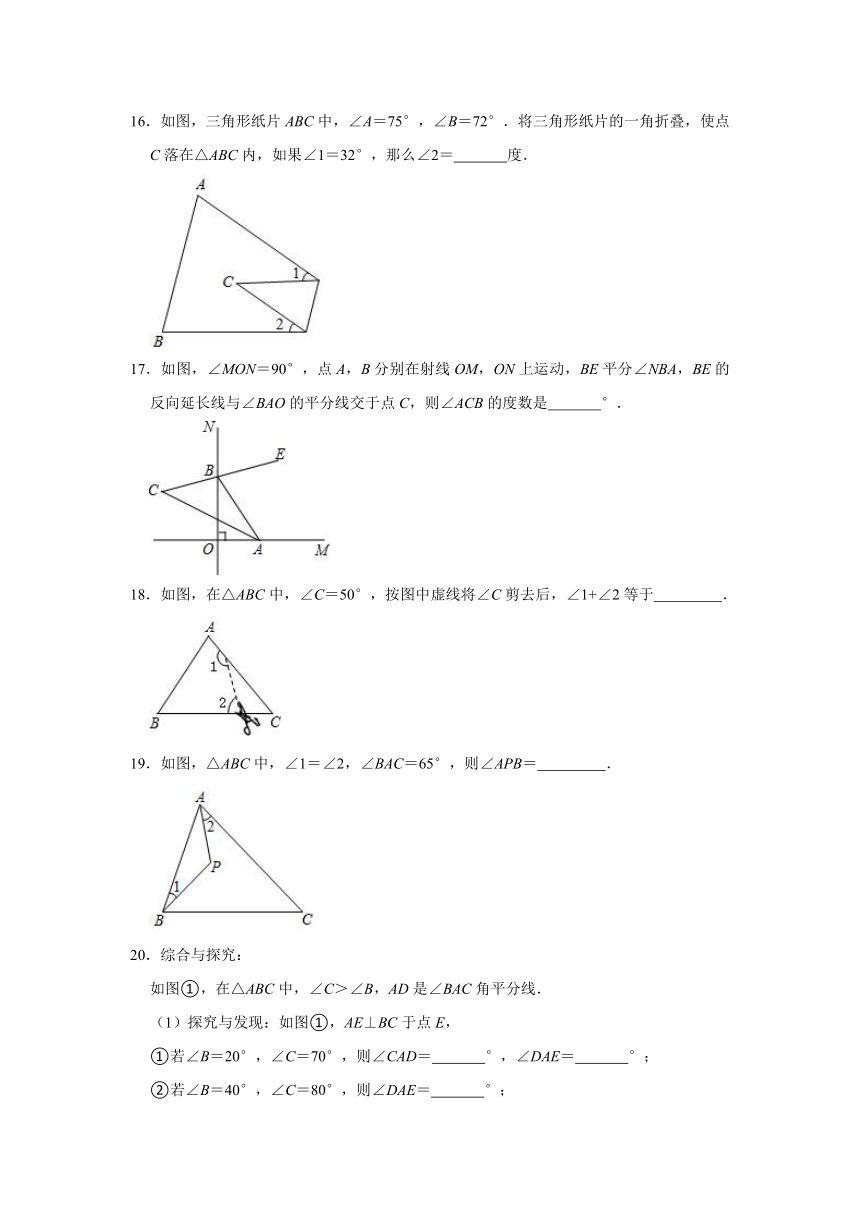
16.如图,三角形纸片ABC中,∠A=75°,∠B=72°.将三角形纸片的一角折叠,使点C落在△ABC内,如果∠1=32°,那么∠2= 度.
17.如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠NBA,BE的反向延长线与∠BAO的平分线交于点C,则∠ACB的度数是 °.
18.如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于 .
19.如图,△ABC中,∠1=∠2,∠BAC=65°,则∠APB= .
20.综合与探究:
如图①,在△ABC中,∠C>∠B,AD是∠BAC角平分线.
(1)探究与发现:如图①,AE⊥BC于点E,
①若∠B=20°,∠C=70°,则∠CAD= °,∠DAE= °;
②若∠B=40°,∠C=80°,则∠DAE= °;
③试探究∠DAE与∠B、∠C的数量关系,并说明理由.
(2)判断与思考:如图②,F是AD上一点,FE⊥BC于点E,这时∠DFE与∠B、∠C又有怎样的数量关系?
如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有 个,以点O为交点的“8字型”有 个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAB=3∠CAP,∠CDB=3∠CDP”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
22.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)若∠B=30°,∠ACB=40°,求∠E的度数;
(2)求证:∠BAC=∠B+2∠E.
23.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
参考答案
1.解:选项A:∵∠A=40°,∠B=50°,
∴∠C=180°﹣∠A﹣∠B=90°.
∴△ABC是直角三角形.
选项B:∵∠A=90°,
∴△ABC是直角三角形.
选项C:∵∠A+B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°.
∴∠C=90°.
∴△ABC是直角三角形.
选项D:∵∠A+∠B=2∠C,∠A+∠B+∠C=180°,
∴3∠C=180°.
∴∠C=60°.
∴∠A+∠B=120°.
∴无法确定△ABC是直角三角形.
故选:D.
2.解:设∠A=α°,则∠B=2α°,∠C=3α°,
依题意得:α+2α+3α=180,
解得:α=30,
∴∠C=3α°=3×30°=90°.
∴△ABC为直角三角形.
故选:A.
3.解:∵∠AOB=125°,
∴∠OAB+∠OBA=55°,
∵AE,BF分别是∠BAC和∠ABC的角平分线,它们相交于点O,
∴∠BAC+∠ABC=2(∠OAB+∠OBA)=110°,
∴∠C=70°,
∵AD是BC边上的高,
∴∠ADC=90°,
∴∠CAD=20°,
即∠CAD的度数是20°.
故选:A.
4.解:根据三角板的度数知,∠ABC=∠ACB=45°,∠DBC=30°,
∴∠1=∠DBC+∠ACB=30°+45°=75°,
故选:C.
5.解:A、锐角三角形的三条高在三角形内部,相交于三角形内一点,故本选项错误;
B、三角形的三条中线相交于三角形内一点,故本选项正确;
C、三角形的一个外角大于任何一个不相邻的一个内角,故本选项错误;
D、根据三角形内角和等于180°,三角形最大的一个内角的度数大于或等于60度,故本选项错误;
故选:B.
6.解:在△ABC中,∠A=70°,∠C=30°,
∴∠ABC=180°﹣∠A﹣∠C=80°,
∵BD平分∠ABC,
∴∠ABD=∠ABC=40°,
∵DE∥AB,
∴∠BDE=∠ABD=40°,
故选:B.
7.解:∵AB⊥AC,
∴∠BAC=90°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=90°﹣36°=54°,
∴∠DAC=90°﹣54°=36°,
故选:A.
8.解:∵∠B=70°,
∴∠BEF+∠BFE=110°,
∵翻折,
∴∠BEF=∠DEF,∠BFE=∠DFE,
∴∠BED+∠BFD=2(∠BEF+∠BFE)=2×110°=220°,
∴∠1+∠2=180°×2﹣220°=140°,
故选:C.
9.解:∵AE⊥CD交CD于点F,
∴∠AFC=∠EFC=90°,
∵CD平分∠ACB,
∴∠ACF=∠ECF,
∵∠AFC+∠CAF+∠ACF=180°,∠EFC+∠CEA+∠ECF=180°,
∴∠CAF=∠CEA,
∵∠CEA=∠B+∠BAE,∠B=45°,∠BAE=20°,
∴∠CAE=65°,
∴∠CAF=65°,
故答案为:65°.
10.解:∵AD是△ABC的角平分线,∠BAD=20°,
∴∠BAC=40°,
∴∠FAC=180°﹣∠BAC=180°﹣40°=140°,
∵AE平分∠CAF,
∴∠CAE=70°,
∴∠BAE=40°+70°=110°,
∵∠AED=30°,
∴∠B=180°﹣30°﹣110°=40°,
故答案为:40°.
11.解:∵∠A=68°,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=112°,
∵OB、OC分别平分∠ABC和∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=56°,
∵∠BPC+∠PBC+∠PCB=180°,
∴∠BPC=124°.
故答案为:124°.
12.解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,
∴∠A1=∠A,
同理理可得∠A2=∠A1,∠A3=∠A2,……
则∠A2021=∠A1=.
故答案为:.
13.解:∵BE⊥AE,
∴∠E=∠C=90°,
∵∠ADC=∠BDE,
∴∠CAD=∠DBE=24°,
∵AE平分∠CAB,
∴∠CAB=2∠CAD=2×24°=48°,
故答案为48°.
14.解:∵∠BFA=∠PAC+∠P,∠BFA=∠PBC+∠C,
∴∠PAC+∠P=∠PBC+∠C,
∵∠CAD和∠CBD的平分线相交于点P,
∴∠PAC=∠CAD,∠PBC=∠CBD,
∴∠CAD+∠P=∠CBD+∠C①,
同理:∠CAD+∠D=∠CBD+∠P②,
①﹣②,得∠P﹣∠D=∠C﹣∠P,
整理得,2∠P=∠D+∠C,
故答案为:2∠P=∠D+∠C.
15.解:∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=180°﹣∠ADC﹣∠C=180°﹣90°﹣26°=64°,
∵AE平分∠BAC,
∴∠CAE=∠BAC=×100°=50°,
∴∠DAE=∠CAD﹣∠CAE=64°﹣50°=14°.
故答案为14°.
16.解:如图延长AE、BF交于点C′,连接CC′.
在△ABC′中,∠AC′B=180°﹣72°﹣75°=33°,
∵∠ECF=∠AC′B=33°,∠1=∠ECC′+∠EC′C,∠2=∠FCC′+∠FC′C,
∴∠1+∠2=∠ECC′+∠EC′C+∠FCC′+∠FC′C=2∠AC′B=66°,
∵∠1=32°,
∴∠2=34°,
故答案为:34.
17.解:根据三角形的外角性质,可得∠ABN=∠AOB+∠BAO,
∵BE平分∠NBA,AC平分∠BAO,
∴∠ABE=∠ABN,∠BAC=∠BAO,
∴∠C=∠ABE﹣∠BAC=(∠AOB+∠BAO)﹣∠BAO=∠AOB,
∵∠MON=90°,
∴∠AOB=90°,
∴∠C=×90°=45°.
故答案为:45.
18.解:∵△ABC中,∠C=50°,
∴∠A+∠B=180°﹣∠C=130°,
∵∠A+∠B+∠1+∠2=360°,
∴∠1+∠2=360°﹣130°=230°,
故答案为:230°.
19.解:∵∠1=∠2,∠BAC=∠BAP+∠1=65°,
∴∠BAP+∠2=65°,
∴△ABP中,∠P=180°﹣65°=115°,
故答案为:115°.
20.解:(1)探究与发现:
①在△ABC中,∠B+∠C+∠BAC=180°,∠B=20°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=90°,
∵AD是∠BAC角平分线,
∴∠CAD=∠BAC=×90°=45°,
∵AE⊥BC,
∴∠AEC=90°,
∴∠CAE=90°﹣70°=20°,
∴∠DAE=∠CAD﹣∠CAE=25°,
故答案为:45,25;
②∵∠B=40°,∠C=80°,
∴∠BAC=60°,
∵AD是∠BAC角平分线,
∴∠CAD=∠BAC=30°,
∵AE⊥BC,
∴∠AEC=90°,
∴∠CAE=90°﹣80°=10°,
∴∠DAE=∠CAD﹣∠CAE=20°,
故答案为:20;
③∠DAE=(∠C﹣∠B),理由如下:
在△AEC中,∠AEC+∠C+∠EAC=180°,
∴∠EAC=180°﹣∠AEC﹣∠C=180°﹣90°﹣∠C=90°﹣∠C,
∴∠DAE=∠CAD﹣∠EAC=×(180°﹣∠B﹣∠C)=(90°﹣∠B﹣∠C)﹣( 90°﹣∠C)=(∠C﹣∠B);
(2)判断与思考;∠DFE=(∠C﹣∠B),理由如下:
证明:∵AD平分∠BAC,
∴∠BAD==90°﹣(∠C+∠B),
∵∠ADC为△ABD的外角,
∴∠ADC=∠B+90°﹣(∠C+∠B)=90°+(∠B﹣∠C),
∵FE⊥BC,
∴∠FED=90°,
∴∠DFE=90°﹣[90°+(∠B﹣∠C)]=90°﹣90°﹣(∠B﹣∠C),
∴∠DFE=(∠C﹣∠B).
21.解:(1)证明:在图1中,有∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,
∴∠A+∠C=∠B+∠D;
(2)解:①3;4;
故答案为:3,4;
②以M为交点”8字型“中,有∠P+∠CDP=∠C+∠CAP,
以N为交点”8字型“中,有∠P+∠BAP=∠B+∠BDP
∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,
∵AP、DP分别平分∠CAB和∠BDC,
∴∠BAP=∠CAP,∠CDP=∠BDP,
∴2∠P=∠B+∠C,
∵∠B=100°,∠C=120°,
∴∠P=(∠B+∠C)=(100°+120°)=110°;
③3∠P=∠B+2∠C,其理由是:
∵∠CAB=3∠CAP,∠CDB=3∠CDP,
∴∠BAP=∠CAB,∠BDP=∠CDB,
以M为交点”8字型“中,有∠P+∠CDP=∠C+∠CAP,
以N为交点”8字型“中,有∠P+∠BAP=∠B+∠BDP
∴∠C﹣∠P=∠CDP﹣∠CAP=(∠CDB﹣∠CAB),
∠P﹣∠B=∠BDP﹣∠BAP=(∠CDB﹣∠CAB).
∴2(∠C﹣∠P)=∠P﹣∠B.
∴3∠P=∠B+2∠C.
22.解:(1)∵∠ACB=40°,
∴∠ACD=180°﹣40°=140°,
∵∠B=30°,
∴∠EAC=∠B+∠ACB=70°,
∵CE是△ABC的外角∠ACD的平分线,
∴∠ACE=70°,
∴∠E=180°﹣70°﹣70°=40°;
(2)∵CE平分∠ACD,
∴∠ACE=∠DCE,
∵∠DCE=∠B+∠E,
∴∠ACE=∠B+∠E,
∵∠BAC=∠ACE+∠E,
∴∠BAC=∠B+∠E+∠E=∠B+2∠E.
23.(1)解:∵∠A=80°.
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°﹣(∠ABC+∠ACB)=180°﹣×100°=130°,
(2)∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB=(∠MBC+∠NCB)
=(360°﹣∠ABC﹣∠ACB)=(180°+∠A)=90°+∠A
∴∠Q=180°﹣(90°+∠A)=90°﹣∠A;
(3)延长BC至F,
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A;
∵∠EBQ=∠EBC+∠CBQ
=∠ABC+∠MBC
=(∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°﹣∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则∠A=2(90°﹣∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
1.已知∠A、∠B、∠C是△ABC的三个内角,下列条件不能确定△ABC是直角三角形的是( )
A.∠A=40°,∠B=50° B.∠A=90°
C.∠A+∠B=∠C D.∠A+∠B=2∠C
2.在△ABC中,如果∠A:∠B:∠C=1:2:3,那么△ABC的形状是( )
A.直角三角形 B.锐角三角形
C.等腰三角形 D.等腰直角三角形
3.如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC和∠ABC的角平分线,它们相交于点O,∠AOB=125°,则∠CAD的度数为( )
A.20° B.30° C.45° D.50°
4.将一副三角板按如图方式重叠,则∠1的度数为( )
A.45° B.60° C.75° D.105°
5.下列说法中,正确的是( )
A.三角形的高都在三角形内 B.三角形的三条中线相交于三角形内一点
C.三角形的一个外角大于任何一个内角 D.三角形最大的一个内角的度数可以小于60度
6.如图,在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是( )
A.30° B.40° C.50° D.60°
7.如图,在△ABC中,AB⊥AC,过点A作AD⊥BC交BC于点D,若∠B=36°,则∠DAC的度数为( )
A.36° B.46° C.54° D.64°
8.如图,在△ABC中,∠B=70°,沿图中虚线EF翻折,使得点B落在AC上的点D处,则∠1+∠2等于( )
A.160° B.150° C.140° D.110°
9.如图,在△ABC中,∠B=45°,CD平分∠ACB交AB于点D,过点A作AE⊥CD交BC于点E,交CD于点F,若∠BAE=20°,则∠CAF的大小为 .
10.如图,AD是△ABC的角平分线,△ABC的一个外角的平分线AE交边BC的延长线于点E,且∠BAD=20°,∠E=30°,则∠B的度数为 .
11.如图,在△ABC中,OB,OC分别为∠ABC和∠ACB的平分线,且∠A=68°,则∠BOC= .
12.如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2021为 .
13.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,BE⊥AD交AD的延长线于点E.若∠DBE=24°,则∠CAB= .
14.如图,∠CAD和∠CBD的平分线相交于点P.请写出∠C、∠D、∠P的数量关系 .
15.如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为 .
16.如图,三角形纸片ABC中,∠A=75°,∠B=72°.将三角形纸片的一角折叠,使点C落在△ABC内,如果∠1=32°,那么∠2= 度.
17.如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠NBA,BE的反向延长线与∠BAO的平分线交于点C,则∠ACB的度数是 °.
18.如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于 .
19.如图,△ABC中,∠1=∠2,∠BAC=65°,则∠APB= .
20.综合与探究:
如图①,在△ABC中,∠C>∠B,AD是∠BAC角平分线.
(1)探究与发现:如图①,AE⊥BC于点E,
①若∠B=20°,∠C=70°,则∠CAD= °,∠DAE= °;
②若∠B=40°,∠C=80°,则∠DAE= °;
③试探究∠DAE与∠B、∠C的数量关系,并说明理由.
(2)判断与思考:如图②,F是AD上一点,FE⊥BC于点E,这时∠DFE与∠B、∠C又有怎样的数量关系?
如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有 个,以点O为交点的“8字型”有 个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAB=3∠CAP,∠CDB=3∠CDP”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
22.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)若∠B=30°,∠ACB=40°,求∠E的度数;
(2)求证:∠BAC=∠B+2∠E.
23.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
参考答案
1.解:选项A:∵∠A=40°,∠B=50°,
∴∠C=180°﹣∠A﹣∠B=90°.
∴△ABC是直角三角形.
选项B:∵∠A=90°,
∴△ABC是直角三角形.
选项C:∵∠A+B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°.
∴∠C=90°.
∴△ABC是直角三角形.
选项D:∵∠A+∠B=2∠C,∠A+∠B+∠C=180°,
∴3∠C=180°.
∴∠C=60°.
∴∠A+∠B=120°.
∴无法确定△ABC是直角三角形.
故选:D.
2.解:设∠A=α°,则∠B=2α°,∠C=3α°,
依题意得:α+2α+3α=180,
解得:α=30,
∴∠C=3α°=3×30°=90°.
∴△ABC为直角三角形.
故选:A.
3.解:∵∠AOB=125°,
∴∠OAB+∠OBA=55°,
∵AE,BF分别是∠BAC和∠ABC的角平分线,它们相交于点O,
∴∠BAC+∠ABC=2(∠OAB+∠OBA)=110°,
∴∠C=70°,
∵AD是BC边上的高,
∴∠ADC=90°,
∴∠CAD=20°,
即∠CAD的度数是20°.
故选:A.
4.解:根据三角板的度数知,∠ABC=∠ACB=45°,∠DBC=30°,
∴∠1=∠DBC+∠ACB=30°+45°=75°,
故选:C.
5.解:A、锐角三角形的三条高在三角形内部,相交于三角形内一点,故本选项错误;
B、三角形的三条中线相交于三角形内一点,故本选项正确;
C、三角形的一个外角大于任何一个不相邻的一个内角,故本选项错误;
D、根据三角形内角和等于180°,三角形最大的一个内角的度数大于或等于60度,故本选项错误;
故选:B.
6.解:在△ABC中,∠A=70°,∠C=30°,
∴∠ABC=180°﹣∠A﹣∠C=80°,
∵BD平分∠ABC,
∴∠ABD=∠ABC=40°,
∵DE∥AB,
∴∠BDE=∠ABD=40°,
故选:B.
7.解:∵AB⊥AC,
∴∠BAC=90°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=90°﹣36°=54°,
∴∠DAC=90°﹣54°=36°,
故选:A.
8.解:∵∠B=70°,
∴∠BEF+∠BFE=110°,
∵翻折,
∴∠BEF=∠DEF,∠BFE=∠DFE,
∴∠BED+∠BFD=2(∠BEF+∠BFE)=2×110°=220°,
∴∠1+∠2=180°×2﹣220°=140°,
故选:C.
9.解:∵AE⊥CD交CD于点F,
∴∠AFC=∠EFC=90°,
∵CD平分∠ACB,
∴∠ACF=∠ECF,
∵∠AFC+∠CAF+∠ACF=180°,∠EFC+∠CEA+∠ECF=180°,
∴∠CAF=∠CEA,
∵∠CEA=∠B+∠BAE,∠B=45°,∠BAE=20°,
∴∠CAE=65°,
∴∠CAF=65°,
故答案为:65°.
10.解:∵AD是△ABC的角平分线,∠BAD=20°,
∴∠BAC=40°,
∴∠FAC=180°﹣∠BAC=180°﹣40°=140°,
∵AE平分∠CAF,
∴∠CAE=70°,
∴∠BAE=40°+70°=110°,
∵∠AED=30°,
∴∠B=180°﹣30°﹣110°=40°,
故答案为:40°.
11.解:∵∠A=68°,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=112°,
∵OB、OC分别平分∠ABC和∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=56°,
∵∠BPC+∠PBC+∠PCB=180°,
∴∠BPC=124°.
故答案为:124°.
12.解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,
∴∠A1=∠A,
同理理可得∠A2=∠A1,∠A3=∠A2,……
则∠A2021=∠A1=.
故答案为:.
13.解:∵BE⊥AE,
∴∠E=∠C=90°,
∵∠ADC=∠BDE,
∴∠CAD=∠DBE=24°,
∵AE平分∠CAB,
∴∠CAB=2∠CAD=2×24°=48°,
故答案为48°.
14.解:∵∠BFA=∠PAC+∠P,∠BFA=∠PBC+∠C,
∴∠PAC+∠P=∠PBC+∠C,
∵∠CAD和∠CBD的平分线相交于点P,
∴∠PAC=∠CAD,∠PBC=∠CBD,
∴∠CAD+∠P=∠CBD+∠C①,
同理:∠CAD+∠D=∠CBD+∠P②,
①﹣②,得∠P﹣∠D=∠C﹣∠P,
整理得,2∠P=∠D+∠C,
故答案为:2∠P=∠D+∠C.
15.解:∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=180°﹣∠ADC﹣∠C=180°﹣90°﹣26°=64°,
∵AE平分∠BAC,
∴∠CAE=∠BAC=×100°=50°,
∴∠DAE=∠CAD﹣∠CAE=64°﹣50°=14°.
故答案为14°.
16.解:如图延长AE、BF交于点C′,连接CC′.
在△ABC′中,∠AC′B=180°﹣72°﹣75°=33°,
∵∠ECF=∠AC′B=33°,∠1=∠ECC′+∠EC′C,∠2=∠FCC′+∠FC′C,
∴∠1+∠2=∠ECC′+∠EC′C+∠FCC′+∠FC′C=2∠AC′B=66°,
∵∠1=32°,
∴∠2=34°,
故答案为:34.
17.解:根据三角形的外角性质,可得∠ABN=∠AOB+∠BAO,
∵BE平分∠NBA,AC平分∠BAO,
∴∠ABE=∠ABN,∠BAC=∠BAO,
∴∠C=∠ABE﹣∠BAC=(∠AOB+∠BAO)﹣∠BAO=∠AOB,
∵∠MON=90°,
∴∠AOB=90°,
∴∠C=×90°=45°.
故答案为:45.
18.解:∵△ABC中,∠C=50°,
∴∠A+∠B=180°﹣∠C=130°,
∵∠A+∠B+∠1+∠2=360°,
∴∠1+∠2=360°﹣130°=230°,
故答案为:230°.
19.解:∵∠1=∠2,∠BAC=∠BAP+∠1=65°,
∴∠BAP+∠2=65°,
∴△ABP中,∠P=180°﹣65°=115°,
故答案为:115°.
20.解:(1)探究与发现:
①在△ABC中,∠B+∠C+∠BAC=180°,∠B=20°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=90°,
∵AD是∠BAC角平分线,
∴∠CAD=∠BAC=×90°=45°,
∵AE⊥BC,
∴∠AEC=90°,
∴∠CAE=90°﹣70°=20°,
∴∠DAE=∠CAD﹣∠CAE=25°,
故答案为:45,25;
②∵∠B=40°,∠C=80°,
∴∠BAC=60°,
∵AD是∠BAC角平分线,
∴∠CAD=∠BAC=30°,
∵AE⊥BC,
∴∠AEC=90°,
∴∠CAE=90°﹣80°=10°,
∴∠DAE=∠CAD﹣∠CAE=20°,
故答案为:20;
③∠DAE=(∠C﹣∠B),理由如下:
在△AEC中,∠AEC+∠C+∠EAC=180°,
∴∠EAC=180°﹣∠AEC﹣∠C=180°﹣90°﹣∠C=90°﹣∠C,
∴∠DAE=∠CAD﹣∠EAC=×(180°﹣∠B﹣∠C)=(90°﹣∠B﹣∠C)﹣( 90°﹣∠C)=(∠C﹣∠B);
(2)判断与思考;∠DFE=(∠C﹣∠B),理由如下:
证明:∵AD平分∠BAC,
∴∠BAD==90°﹣(∠C+∠B),
∵∠ADC为△ABD的外角,
∴∠ADC=∠B+90°﹣(∠C+∠B)=90°+(∠B﹣∠C),
∵FE⊥BC,
∴∠FED=90°,
∴∠DFE=90°﹣[90°+(∠B﹣∠C)]=90°﹣90°﹣(∠B﹣∠C),
∴∠DFE=(∠C﹣∠B).
21.解:(1)证明:在图1中,有∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,
∴∠A+∠C=∠B+∠D;
(2)解:①3;4;
故答案为:3,4;
②以M为交点”8字型“中,有∠P+∠CDP=∠C+∠CAP,
以N为交点”8字型“中,有∠P+∠BAP=∠B+∠BDP
∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,
∵AP、DP分别平分∠CAB和∠BDC,
∴∠BAP=∠CAP,∠CDP=∠BDP,
∴2∠P=∠B+∠C,
∵∠B=100°,∠C=120°,
∴∠P=(∠B+∠C)=(100°+120°)=110°;
③3∠P=∠B+2∠C,其理由是:
∵∠CAB=3∠CAP,∠CDB=3∠CDP,
∴∠BAP=∠CAB,∠BDP=∠CDB,
以M为交点”8字型“中,有∠P+∠CDP=∠C+∠CAP,
以N为交点”8字型“中,有∠P+∠BAP=∠B+∠BDP
∴∠C﹣∠P=∠CDP﹣∠CAP=(∠CDB﹣∠CAB),
∠P﹣∠B=∠BDP﹣∠BAP=(∠CDB﹣∠CAB).
∴2(∠C﹣∠P)=∠P﹣∠B.
∴3∠P=∠B+2∠C.
22.解:(1)∵∠ACB=40°,
∴∠ACD=180°﹣40°=140°,
∵∠B=30°,
∴∠EAC=∠B+∠ACB=70°,
∵CE是△ABC的外角∠ACD的平分线,
∴∠ACE=70°,
∴∠E=180°﹣70°﹣70°=40°;
(2)∵CE平分∠ACD,
∴∠ACE=∠DCE,
∵∠DCE=∠B+∠E,
∴∠ACE=∠B+∠E,
∵∠BAC=∠ACE+∠E,
∴∠BAC=∠B+∠E+∠E=∠B+2∠E.
23.(1)解:∵∠A=80°.
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°﹣(∠ABC+∠ACB)=180°﹣×100°=130°,
(2)∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB=(∠MBC+∠NCB)
=(360°﹣∠ABC﹣∠ACB)=(180°+∠A)=90°+∠A
∴∠Q=180°﹣(90°+∠A)=90°﹣∠A;
(3)延长BC至F,
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A;
∵∠EBQ=∠EBC+∠CBQ
=∠ABC+∠MBC
=(∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°﹣∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则∠A=2(90°﹣∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
