11.2与三角形有关的角 同步专题提升训练 2021—2022学年人教版八年级数学上册 (Word版 附答案)
文档属性
| 名称 | 11.2与三角形有关的角 同步专题提升训练 2021—2022学年人教版八年级数学上册 (Word版 附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 162.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览


文档简介
2021年人教版八年级数学上册《11.2与三角形有关的角》同步专题提升训练(附答案)
1.如图,AB与CD相交于点O,则下列结论正确的是( )
A.∠1=∠2 B.∠1=∠D C.∠C=∠D D.∠B+∠C=180°
2.如果三角形三个内角分别是x°,x°,y°,则下列结论正确的是( )
A.x+2y=180 B.2x+y=180 C.2x﹣y=180 D.3x+y=180
3.如图,△ABC的高CD、BE相交于点O,如果∠A=60°,那么∠BOC的大小为( )
A.60° B.100° C.120° D.130°
4.如图,在△ABC中,∠C=90°,EF∥AB,∠1=50°,则∠B的度数为( )
A.50° B.60° C.30° D.40°
5.在△ABC中,若∠A﹣∠B=∠C,则此三角形是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.无法确定
6.如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
A.59° B.60° C.56° D.22°
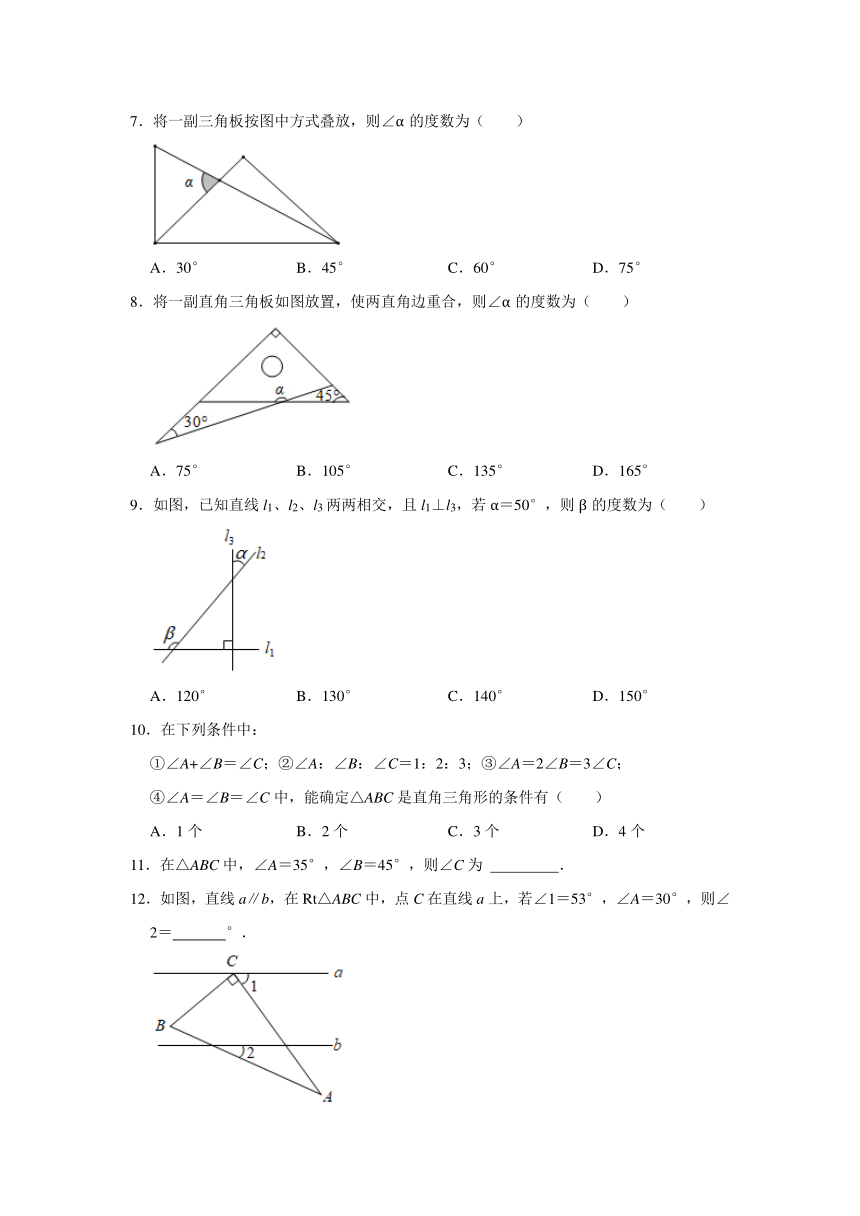
7.将一副三角板按图中方式叠放,则∠α的度数为( )
A.30° B.45° C.60° D.75°
8.将一副直角三角板如图放置,使两直角边重合,则∠α的度数为( )
A.75° B.105° C.135° D.165°
9.如图,已知直线l1、l2、l3两两相交,且l1⊥l3,若α=50°,则β的度数为( )
A.120° B.130° C.140° D.150°
10.在下列条件中:
①∠A+∠B=∠C;②∠A:∠B:∠C=1:2:3;③∠A=2∠B=3∠C;
④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
11.在△ABC中,∠A=35°,∠B=45°,则∠C为 .
12.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=53°,∠A=30°,则∠2= °.
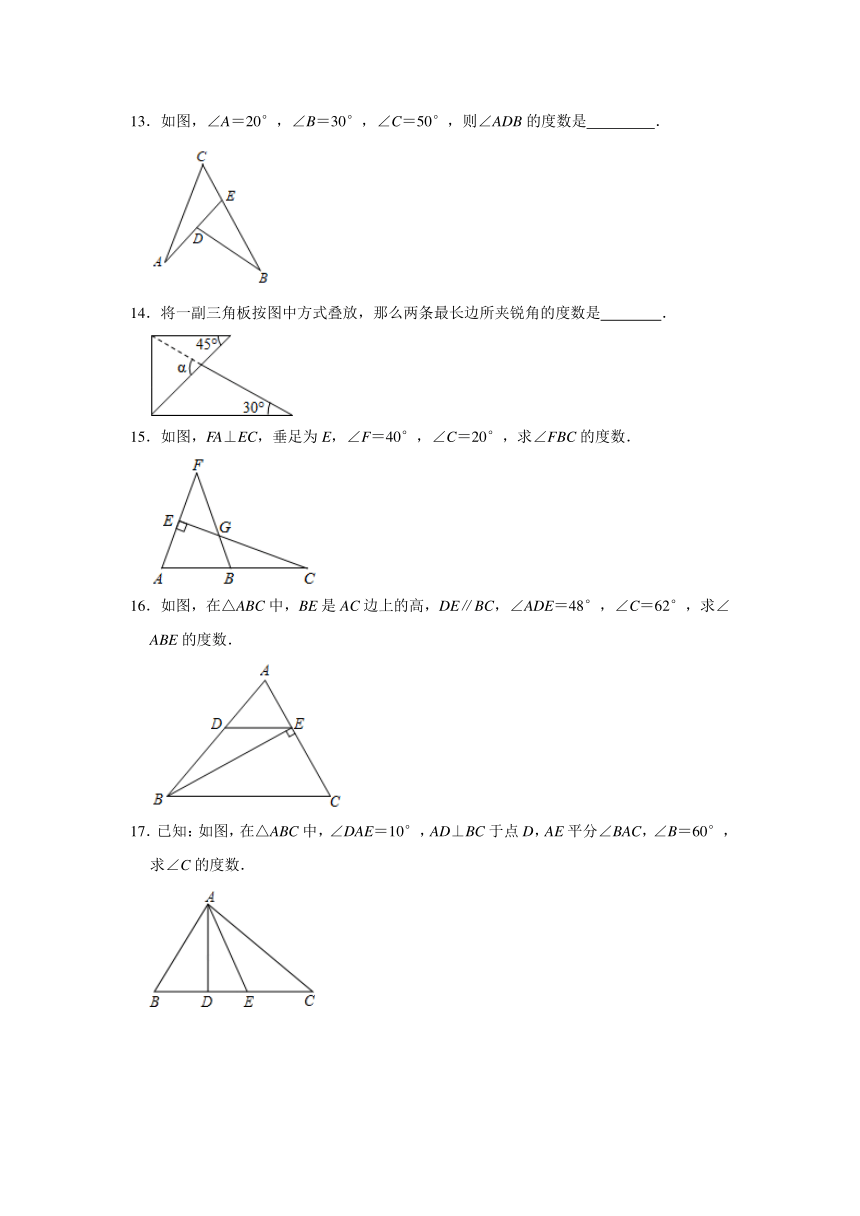
13.如图,∠A=20°,∠B=30°,∠C=50°,则∠ADB的度数是 .
14.将一副三角板按图中方式叠放,那么两条最长边所夹锐角的度数是 .
15.如图,FA⊥EC,垂足为E,∠F=40°,∠C=20°,求∠FBC的度数.
16.如图,在△ABC中,BE是AC边上的高,DE∥BC,∠ADE=48°,∠C=62°,求∠ABE的度数.
17.已知:如图,在△ABC中,∠DAE=10°,AD⊥BC于点D,AE平分∠BAC,∠B=60°,求∠C的度数.
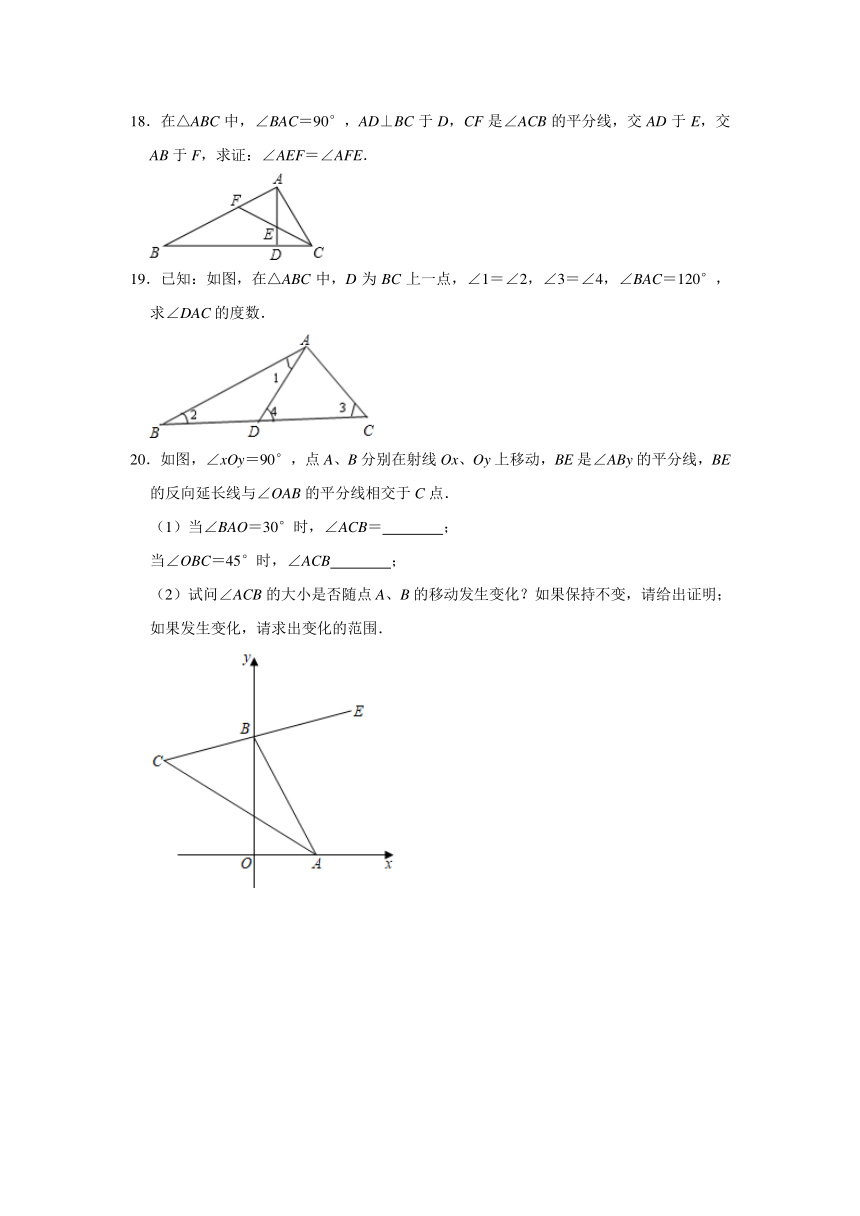
18.在△ABC中,∠BAC=90°,AD⊥BC于D,CF是∠ACB的平分线,交AD于E,交AB于F,求证:∠AEF=∠AFE.
19.已知:如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=120°,求∠DAC的度数.
20.如图,∠xOy=90°,点A、B分别在射线Ox、Oy上移动,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于C点.
(1)当∠BAO=30°时,∠ACB= ;
当∠OBC=45°时,∠ACB ;
(2)试问∠ACB的大小是否随点A、B的移动发生变化?如果保持不变,请给出证明;如果发生变化,请求出变化的范围.
参考答案
1.解:选项A、∵∠1与∠2互为对顶角,∴∠1=∠2,故选项A符合题意;
选项B、∵∠1=∠D+∠A,∴∠1>∠D,故选项B不符合题意;
选项C、∵AD与BC是否平行不能确定,∴∠C与∠D不一定相等,故选项C不符合题意;
选项D、∵∠B+∠C+∠BOC=180°,∴∠B+∠C<180°,故选项D不符合题意;
故选:A.
2.解:∵三角形三个内角分别是x°,x°,y°,
∴x+x+y=180(三角形的内角和等于180°),
∴2x+y=180.
故选:B.
3.解:如图,
∵CD、BE均为△ABC的高,
∴∠BEC=∠ADC=90°,
∵∠A=60°,
∴∠OCE=180°﹣∠ADC﹣∠A=180°﹣90°﹣60°=30°,
则∠BOC=∠BEC+∠OCE=90°+30°=120°.
故选:C.
4.解:∵EF∥AB,
∴∠A=∠1=50°,
∵△ABC是直角三角形,
∴∠B=90°﹣∠A=90°﹣50°=40°.
故选:D.
5.解:∵∠A﹣∠B=∠C,
∴∠A=∠B+∠C,
∵∠A+∠B+∠C=180°,
∴2∠A=180°,
∴∠A=90°,
∴△ABC是直角三角形,
故选:B.
6.解:∵BE为△ABC的高,
∴∠AEB=90°
∵∠C=70°,∠ABC=48°,
∴∠CAB=62°,
∵AF是角平分线,
∴∠1=∠CAB=31°,
在△AEF中,∠EFA=180°﹣31°﹣90°=59°.
∴∠3=∠EFA=59°,
故选:A.
7.解:由题意得,∠DBC=45°,∠ACB=30°,
∴∠α=30°+45°=75°,
故选:D.
8.解:∠AOC=∠DAB﹣∠C=15°,
∴∠α=180°﹣15°=165°,
故选:D.
9.解:如图,根据对顶角相等得:∠1=∠α=50°,
∵l1⊥l3,
∴∠2=90°.
∵∠β是三角形的外角,
∴∠β=∠1+∠2=50°+90°=140°,
故选:C.
10.解:①∠A+∠B=∠C,是直角三角形;
②∠A:∠B:∠C=1:2:3,是直角三角形;
③∠A=2∠B=3∠C,则设∠A=x,∠B=,∠C=,则x++=180°,解得x=,
∴∠A=,,,
∴△ABC不是直角三角形;
④∠A=∠B=∠C,不是直角三角形,是等边三角形,
能确定△ABC是直角三角形的条件有2个,
故选:B.
11.解:∵∠A+∠B+∠C=180°,
∴∠C=180°﹣∠A﹣∠B=180°﹣35°﹣45°=100°.
故答案为:100°.
12.
解:过B点做BM∥a
∵∠BCA=90°,∠1=53°.
∴∠3=37°.
∵∠A=30°.
∴∠CBA=60°.
∵a∥BM.
∴∠3=∠4=37°.
∵a∥b,BM∥b.
∴BM∥b.
∴∠5=∠2=60°﹣37°=23°.
13.解:∵∠AEB是△ACE的一个外角,
∴∠AEB=∠A+∠C=20°+50°=70°,
∵∠ADB是△DEB的一个外角,
∴∠ADB=∠AEB+∠B=70°+30°=100°,
故答案为:100°.
14.解:如图,由题意,可得∠2=45°,∠1+∠2=90°,
∴∠1=90°﹣45°=45°,
∴∠α=∠1+30°=45°+30°=75°.
故答案为:75°.
15.解:在△AEC 中,FA⊥EC,
∴∠AEC=90°,
∴∠A=90°﹣∠C=70°.
∴∠FBC=∠A+∠F=70°+40°=110°.
16.解:∵DE∥BC,∠ADE=48°,
∴∠ABC=∠ADE=48°,
∵BE是AC边上的高,
∴∠BEC=90°,
∵∠C=62°,
∴∠EBC=90﹣∠C=28°,
∴∠ABE=∠ABC﹣∠EBC=48°﹣28°=20°.
17.解:∵AD⊥BC,∠B=60°,
∴在△ABD中,∠BAD=180°﹣90°﹣60°=30°,
又∵∠DAE=10°,
∴∠BAE=∠BAD+∠DAE=30°+10°=40°,
又∵AE平分∠BAC,
∴∠BAC=2∠BAE=80°,
∴在△ABC中,∠C=180°﹣∠BAC﹣∠B=180°﹣80°﹣60°=40°.
答:∠C的度数是40°.
18.证明:∵CF是∠ACB的平分线,
∴∠ACF=∠BCF,
∵∠BAC=90°,AD⊥BC,
∴∠ACF+∠AFE=90°,∠BCF+∠CED=90°,
∴∠AFE=∠CED,
∵∠AEF=∠CED(对顶角相等),
∴∠AEF=∠AFE.
19.解:∵∠BAC=120°,
∴∠2+∠3=60°①
∵∠1=∠2,
∴∠4=∠3=∠1+∠2=2∠2②
把②代入①得:3∠2=60°,
∠2=20°.
∴∠DAC=120°﹣20°=100°.
20.解:(1)∵∠xOy=90°,∠BAO=30°,
∴∠ABy=120°,
∵AC平分∠OAB,BE平分∠yBA,
∴∠CAB=∠BAO=15°,∠EBA=∠yBA=60°,
∵∠EBA=∠ACB+∠CAB,
∴∠ACB=∠EBA﹣∠CAB=60°﹣15°=45°;
∵∠OBC=45°,
∴∠yBE=45°,
∵∠yBA=90°,
∴BA∥OA,即∠BAO不存在,
∴∠ACB不存在;
故答案为:45;不存在;
(2)∠ACB的大小不变化.
理由:∵AC平分∠OAB,BE平分∠yBA,
∴∠CAB=∠OAB,∠EBA=∠yBA,
∵∠EBA=∠C+∠CAB,
∴∠C=∠EBA﹣∠CAB=∠yBA﹣∠OAB=(∠yBA﹣∠OAB),
∵∠yBA﹣∠OAB=90°,
∴∠C=×90°=45°,
即:∠ACB的大小不发生变化
1.如图,AB与CD相交于点O,则下列结论正确的是( )
A.∠1=∠2 B.∠1=∠D C.∠C=∠D D.∠B+∠C=180°
2.如果三角形三个内角分别是x°,x°,y°,则下列结论正确的是( )
A.x+2y=180 B.2x+y=180 C.2x﹣y=180 D.3x+y=180
3.如图,△ABC的高CD、BE相交于点O,如果∠A=60°,那么∠BOC的大小为( )
A.60° B.100° C.120° D.130°
4.如图,在△ABC中,∠C=90°,EF∥AB,∠1=50°,则∠B的度数为( )
A.50° B.60° C.30° D.40°
5.在△ABC中,若∠A﹣∠B=∠C,则此三角形是( )
A.钝角三角形 B.直角三角形 C.锐角三角形 D.无法确定
6.如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
A.59° B.60° C.56° D.22°
7.将一副三角板按图中方式叠放,则∠α的度数为( )
A.30° B.45° C.60° D.75°
8.将一副直角三角板如图放置,使两直角边重合,则∠α的度数为( )
A.75° B.105° C.135° D.165°
9.如图,已知直线l1、l2、l3两两相交,且l1⊥l3,若α=50°,则β的度数为( )
A.120° B.130° C.140° D.150°
10.在下列条件中:
①∠A+∠B=∠C;②∠A:∠B:∠C=1:2:3;③∠A=2∠B=3∠C;
④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
11.在△ABC中,∠A=35°,∠B=45°,则∠C为 .
12.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=53°,∠A=30°,则∠2= °.
13.如图,∠A=20°,∠B=30°,∠C=50°,则∠ADB的度数是 .
14.将一副三角板按图中方式叠放,那么两条最长边所夹锐角的度数是 .
15.如图,FA⊥EC,垂足为E,∠F=40°,∠C=20°,求∠FBC的度数.
16.如图,在△ABC中,BE是AC边上的高,DE∥BC,∠ADE=48°,∠C=62°,求∠ABE的度数.
17.已知:如图,在△ABC中,∠DAE=10°,AD⊥BC于点D,AE平分∠BAC,∠B=60°,求∠C的度数.
18.在△ABC中,∠BAC=90°,AD⊥BC于D,CF是∠ACB的平分线,交AD于E,交AB于F,求证:∠AEF=∠AFE.
19.已知:如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=120°,求∠DAC的度数.
20.如图,∠xOy=90°,点A、B分别在射线Ox、Oy上移动,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于C点.
(1)当∠BAO=30°时,∠ACB= ;
当∠OBC=45°时,∠ACB ;
(2)试问∠ACB的大小是否随点A、B的移动发生变化?如果保持不变,请给出证明;如果发生变化,请求出变化的范围.
参考答案
1.解:选项A、∵∠1与∠2互为对顶角,∴∠1=∠2,故选项A符合题意;
选项B、∵∠1=∠D+∠A,∴∠1>∠D,故选项B不符合题意;
选项C、∵AD与BC是否平行不能确定,∴∠C与∠D不一定相等,故选项C不符合题意;
选项D、∵∠B+∠C+∠BOC=180°,∴∠B+∠C<180°,故选项D不符合题意;
故选:A.
2.解:∵三角形三个内角分别是x°,x°,y°,
∴x+x+y=180(三角形的内角和等于180°),
∴2x+y=180.
故选:B.
3.解:如图,
∵CD、BE均为△ABC的高,
∴∠BEC=∠ADC=90°,
∵∠A=60°,
∴∠OCE=180°﹣∠ADC﹣∠A=180°﹣90°﹣60°=30°,
则∠BOC=∠BEC+∠OCE=90°+30°=120°.
故选:C.
4.解:∵EF∥AB,
∴∠A=∠1=50°,
∵△ABC是直角三角形,
∴∠B=90°﹣∠A=90°﹣50°=40°.
故选:D.
5.解:∵∠A﹣∠B=∠C,
∴∠A=∠B+∠C,
∵∠A+∠B+∠C=180°,
∴2∠A=180°,
∴∠A=90°,
∴△ABC是直角三角形,
故选:B.
6.解:∵BE为△ABC的高,
∴∠AEB=90°
∵∠C=70°,∠ABC=48°,
∴∠CAB=62°,
∵AF是角平分线,
∴∠1=∠CAB=31°,
在△AEF中,∠EFA=180°﹣31°﹣90°=59°.
∴∠3=∠EFA=59°,
故选:A.
7.解:由题意得,∠DBC=45°,∠ACB=30°,
∴∠α=30°+45°=75°,
故选:D.
8.解:∠AOC=∠DAB﹣∠C=15°,
∴∠α=180°﹣15°=165°,
故选:D.
9.解:如图,根据对顶角相等得:∠1=∠α=50°,
∵l1⊥l3,
∴∠2=90°.
∵∠β是三角形的外角,
∴∠β=∠1+∠2=50°+90°=140°,
故选:C.
10.解:①∠A+∠B=∠C,是直角三角形;
②∠A:∠B:∠C=1:2:3,是直角三角形;
③∠A=2∠B=3∠C,则设∠A=x,∠B=,∠C=,则x++=180°,解得x=,
∴∠A=,,,
∴△ABC不是直角三角形;
④∠A=∠B=∠C,不是直角三角形,是等边三角形,
能确定△ABC是直角三角形的条件有2个,
故选:B.
11.解:∵∠A+∠B+∠C=180°,
∴∠C=180°﹣∠A﹣∠B=180°﹣35°﹣45°=100°.
故答案为:100°.
12.
解:过B点做BM∥a
∵∠BCA=90°,∠1=53°.
∴∠3=37°.
∵∠A=30°.
∴∠CBA=60°.
∵a∥BM.
∴∠3=∠4=37°.
∵a∥b,BM∥b.
∴BM∥b.
∴∠5=∠2=60°﹣37°=23°.
13.解:∵∠AEB是△ACE的一个外角,
∴∠AEB=∠A+∠C=20°+50°=70°,
∵∠ADB是△DEB的一个外角,
∴∠ADB=∠AEB+∠B=70°+30°=100°,
故答案为:100°.
14.解:如图,由题意,可得∠2=45°,∠1+∠2=90°,
∴∠1=90°﹣45°=45°,
∴∠α=∠1+30°=45°+30°=75°.
故答案为:75°.
15.解:在△AEC 中,FA⊥EC,
∴∠AEC=90°,
∴∠A=90°﹣∠C=70°.
∴∠FBC=∠A+∠F=70°+40°=110°.
16.解:∵DE∥BC,∠ADE=48°,
∴∠ABC=∠ADE=48°,
∵BE是AC边上的高,
∴∠BEC=90°,
∵∠C=62°,
∴∠EBC=90﹣∠C=28°,
∴∠ABE=∠ABC﹣∠EBC=48°﹣28°=20°.
17.解:∵AD⊥BC,∠B=60°,
∴在△ABD中,∠BAD=180°﹣90°﹣60°=30°,
又∵∠DAE=10°,
∴∠BAE=∠BAD+∠DAE=30°+10°=40°,
又∵AE平分∠BAC,
∴∠BAC=2∠BAE=80°,
∴在△ABC中,∠C=180°﹣∠BAC﹣∠B=180°﹣80°﹣60°=40°.
答:∠C的度数是40°.
18.证明:∵CF是∠ACB的平分线,
∴∠ACF=∠BCF,
∵∠BAC=90°,AD⊥BC,
∴∠ACF+∠AFE=90°,∠BCF+∠CED=90°,
∴∠AFE=∠CED,
∵∠AEF=∠CED(对顶角相等),
∴∠AEF=∠AFE.
19.解:∵∠BAC=120°,
∴∠2+∠3=60°①
∵∠1=∠2,
∴∠4=∠3=∠1+∠2=2∠2②
把②代入①得:3∠2=60°,
∠2=20°.
∴∠DAC=120°﹣20°=100°.
20.解:(1)∵∠xOy=90°,∠BAO=30°,
∴∠ABy=120°,
∵AC平分∠OAB,BE平分∠yBA,
∴∠CAB=∠BAO=15°,∠EBA=∠yBA=60°,
∵∠EBA=∠ACB+∠CAB,
∴∠ACB=∠EBA﹣∠CAB=60°﹣15°=45°;
∵∠OBC=45°,
∴∠yBE=45°,
∵∠yBA=90°,
∴BA∥OA,即∠BAO不存在,
∴∠ACB不存在;
故答案为:45;不存在;
(2)∠ACB的大小不变化.
理由:∵AC平分∠OAB,BE平分∠yBA,
∴∠CAB=∠OAB,∠EBA=∠yBA,
∵∠EBA=∠C+∠CAB,
∴∠C=∠EBA﹣∠CAB=∠yBA﹣∠OAB=(∠yBA﹣∠OAB),
∵∠yBA﹣∠OAB=90°,
∴∠C=×90°=45°,
即:∠ACB的大小不发生变化
