2021-2022学年人教版数学八年级上册11.3多边形及其内角和 同步训练卷 (word版有答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册11.3多边形及其内角和 同步训练卷 (word版有答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 126.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览


文档简介
人教版2021年八年级上册11.3多边形及其内角和 同步训练卷
一.选择题
1.正六边形的外角和为( )
A.180° B.360° C.540° D.720°
2.八边形的内角和为( )
A.720° B.900° C.1080° D.1440°
3.一个n边形的每一个外角都是60°,则n等于( )
A.3 B.4 C.6 D.5
4.如图,五边形ABCDE是正五边形,则x为( )
A.30° B.35° C.36° D.45°
5.一个多边形截去一个角后,形成一个六边形,那么原多边形边数为( )
A.5 B.5或6 C.5或7 D.5或6或7
二.填空题
6.已知一个多边形的内角和为1080°,则它的边数为 .
7.已知一个多边形的每个外角都等于45°,则它的内角和为 .
8.若一个正多边形的内角是外角的3倍,则这个正多边形的边数为 .
9.如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,n边形可以分割出 个三角形.
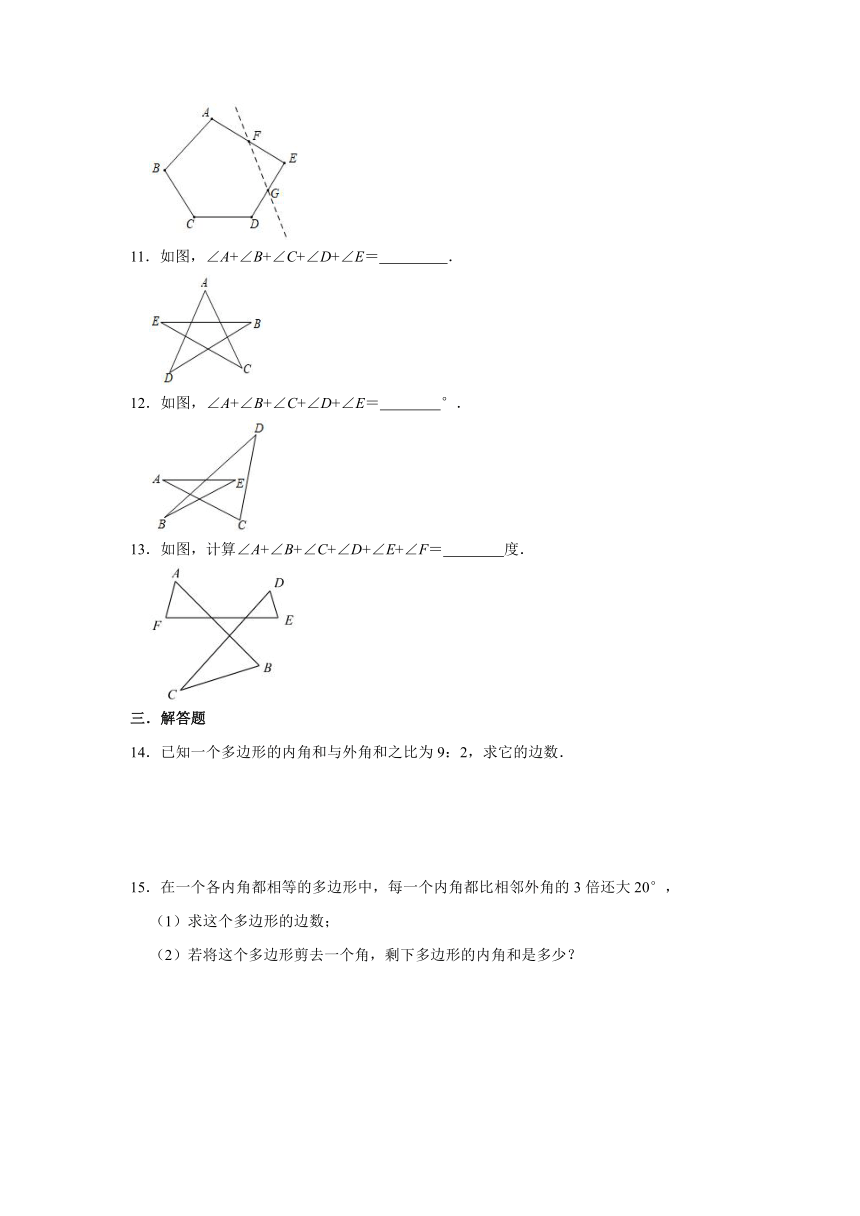
10.如图,将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长 (填:大或小),理由为 .
11.如图,∠A+∠B+∠C+∠D+∠E= .
12.如图,∠A+∠B+∠C+∠D+∠E= °.
13.如图,计算∠A+∠B+∠C+∠D+∠E+∠F= 度.
三.解答题
14.已知一个多边形的内角和与外角和之比为9:2,求它的边数.
15.在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
16.如果一个多边形的各边都相等且各角也都相等,那么这样的多边形叫做正多边形,如正三角形就是等边三角形,正四边形就是正方形,如下图,就是一组正多边形,
(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 3 4 5 6 … n
∠α的度数 …
(2)根据规律,计算正八边形中的∠α的度数;
(3)是否存在正n边形使得∠α=21°?若存在,请求出n的值,若不存在,请说明理由.
17.“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
参考答案
一.选择题
1.解:正六边形的外角和是360°.
故选:B.
2.解:(8﹣2)?180°=1080°.
故选:C.
3.解:∵n边形的每一个外角都是60°,
∴此n边形是正n边形,
n=360°÷60°=6,
故选:C.
4.解:因为五边形ABCDE是正五边形,
所以∠E=∠CDE==108°,AE=DE,
所以,
所以x=∠CDE﹣∠1﹣∠3=36°.
故选:C.
5.解:如图可知,原来多边形的边数可能是5,6,7.
故选:D.
二.填空题
6.解:设这个多边形的边数为n,
根据题意得:180(n﹣2)=1080,
解得:n=8.
故答案为:8.
7.解:∵一个多边形的每个外角都等于45°,
∴多边形的边数为360°÷45°=8,
∴这个多边形的内角和=180°×(8﹣2)=1080°.
故答案为:1080°.
8.解:设正多边形的边数为n,由题意得:
(n﹣2)?180°=3×360°,
解得:n=8,
故答案为:8.
9.解:n边形可以分割出(n﹣1)个三角形.
10.解:将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长小,理由是两点之间,线段最短.
故答案为:小;两点之间,线段最短.
11.解:∵∠CFD=∠A+∠D,∠CGF=∠B+∠E,
∴∠A+∠D+∠B+∠E=∠CFD+∠CGF,
∵∠CFD+∠CGF+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
故答案为:180°.
12.解:如图,设线段BD,BE分别与线段AC交于点N,M.
∵∠AMB=∠A+∠E,∠DNC=∠B+∠AMB,∠DNC+∠D+∠C=180°,
∴∠A+∠B+∠D+∠E+∠C=180°,
故答案为:180.
13.解:
∵∠1=∠A+∠F,∠2=∠D+∠E,∠3=∠B+∠C,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠1+∠2+∠3,
∠1、∠2、∠3是△MNP的三个不同外角,
∵∠1+∠2+∠3=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360.
三.解答题
14.解:设该多边形的边数为n
则(n﹣2)×180°:360=9:2,
解得:n=11.
故它的边数为11.
15.解:(1)设多边形的一个外角为α,则与其相邻的内角等于3α+20°,
由题意,得(3α+20)+α=180°,解得α=40°.
即多边形的每个外角为40°.
又∵多边形的外角和为360°,
∴多边形的外角个数==9.
∴多边形的边数=9,
答:这个多边形的边数是9;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
当截线为经过对角2个顶点的直线时,多边形的边数减少了1条边,内角和=(9﹣2﹣1)×180°=1080°;
当截线为经过多边形一组对边的直线时,多边形的边数不变,内角和=(9﹣2)×180°=1260°;
当截线为只经过正方形一组邻边的一条直线时,多边形的边数增加一条边,内角和=(9﹣2+1)×180°=1440°.
答:将这个多边形剪去一个角,剩下多边形的内角和是1080°或1260°或1440°.
16.解:(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 3 4 5 6 … n
∠α的度数 60° 45° 36° 30° … ()°
(2)根据规律,计算正八边形中的∠α=()°=22.5°;
(3)不存在,理由如下:
设存在正n边形使得∠α=21°,
得∠α=21°=()°.
解得n=8,n是正整数,n=8(不符合题意要舍去),
不存在正n边形使得∠α=21°.
17.解:(1)∵∠1=∠2+∠D=∠B+∠E+∠D,∠1+∠A+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)∵∠1=∠2+∠F=∠B+∠E+∠F,∠1+∠A+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°;
(3)根据图中可得出规律∠A+∠B+∠C+∠D+∠E=180°,每截去一个角则会增加180度,
所以当截去5个角时增加了180×5度,
则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=1080°.
一.选择题
1.正六边形的外角和为( )
A.180° B.360° C.540° D.720°
2.八边形的内角和为( )
A.720° B.900° C.1080° D.1440°
3.一个n边形的每一个外角都是60°,则n等于( )
A.3 B.4 C.6 D.5
4.如图,五边形ABCDE是正五边形,则x为( )
A.30° B.35° C.36° D.45°
5.一个多边形截去一个角后,形成一个六边形,那么原多边形边数为( )
A.5 B.5或6 C.5或7 D.5或6或7
二.填空题
6.已知一个多边形的内角和为1080°,则它的边数为 .
7.已知一个多边形的每个外角都等于45°,则它的内角和为 .
8.若一个正多边形的内角是外角的3倍,则这个正多边形的边数为 .
9.如图所示,将多边形分割成三角形、图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,n边形可以分割出 个三角形.
10.如图,将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长 (填:大或小),理由为 .
11.如图,∠A+∠B+∠C+∠D+∠E= .
12.如图,∠A+∠B+∠C+∠D+∠E= °.
13.如图,计算∠A+∠B+∠C+∠D+∠E+∠F= 度.
三.解答题
14.已知一个多边形的内角和与外角和之比为9:2,求它的边数.
15.在一个各内角都相等的多边形中,每一个内角都比相邻外角的3倍还大20°,
(1)求这个多边形的边数;
(2)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
16.如果一个多边形的各边都相等且各角也都相等,那么这样的多边形叫做正多边形,如正三角形就是等边三角形,正四边形就是正方形,如下图,就是一组正多边形,
(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 3 4 5 6 … n
∠α的度数 …
(2)根据规律,计算正八边形中的∠α的度数;
(3)是否存在正n边形使得∠α=21°?若存在,请求出n的值,若不存在,请说明理由.
17.“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
参考答案
一.选择题
1.解:正六边形的外角和是360°.
故选:B.
2.解:(8﹣2)?180°=1080°.
故选:C.
3.解:∵n边形的每一个外角都是60°,
∴此n边形是正n边形,
n=360°÷60°=6,
故选:C.
4.解:因为五边形ABCDE是正五边形,
所以∠E=∠CDE==108°,AE=DE,
所以,
所以x=∠CDE﹣∠1﹣∠3=36°.
故选:C.
5.解:如图可知,原来多边形的边数可能是5,6,7.
故选:D.
二.填空题
6.解:设这个多边形的边数为n,
根据题意得:180(n﹣2)=1080,
解得:n=8.
故答案为:8.
7.解:∵一个多边形的每个外角都等于45°,
∴多边形的边数为360°÷45°=8,
∴这个多边形的内角和=180°×(8﹣2)=1080°.
故答案为:1080°.
8.解:设正多边形的边数为n,由题意得:
(n﹣2)?180°=3×360°,
解得:n=8,
故答案为:8.
9.解:n边形可以分割出(n﹣1)个三角形.
10.解:将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长小,理由是两点之间,线段最短.
故答案为:小;两点之间,线段最短.
11.解:∵∠CFD=∠A+∠D,∠CGF=∠B+∠E,
∴∠A+∠D+∠B+∠E=∠CFD+∠CGF,
∵∠CFD+∠CGF+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
故答案为:180°.
12.解:如图,设线段BD,BE分别与线段AC交于点N,M.
∵∠AMB=∠A+∠E,∠DNC=∠B+∠AMB,∠DNC+∠D+∠C=180°,
∴∠A+∠B+∠D+∠E+∠C=180°,
故答案为:180.
13.解:
∵∠1=∠A+∠F,∠2=∠D+∠E,∠3=∠B+∠C,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠1+∠2+∠3,
∠1、∠2、∠3是△MNP的三个不同外角,
∵∠1+∠2+∠3=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360.
三.解答题
14.解:设该多边形的边数为n
则(n﹣2)×180°:360=9:2,
解得:n=11.
故它的边数为11.
15.解:(1)设多边形的一个外角为α,则与其相邻的内角等于3α+20°,
由题意,得(3α+20)+α=180°,解得α=40°.
即多边形的每个外角为40°.
又∵多边形的外角和为360°,
∴多边形的外角个数==9.
∴多边形的边数=9,
答:这个多边形的边数是9;
(2)因为剪掉一个角以后,多边形的边数可能增加了1条,也可能减少了1条,或者不变,
当截线为经过对角2个顶点的直线时,多边形的边数减少了1条边,内角和=(9﹣2﹣1)×180°=1080°;
当截线为经过多边形一组对边的直线时,多边形的边数不变,内角和=(9﹣2)×180°=1260°;
当截线为只经过正方形一组邻边的一条直线时,多边形的边数增加一条边,内角和=(9﹣2+1)×180°=1440°.
答:将这个多边形剪去一个角,剩下多边形的内角和是1080°或1260°或1440°.
16.解:(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 3 4 5 6 … n
∠α的度数 60° 45° 36° 30° … ()°
(2)根据规律,计算正八边形中的∠α=()°=22.5°;
(3)不存在,理由如下:
设存在正n边形使得∠α=21°,
得∠α=21°=()°.
解得n=8,n是正整数,n=8(不符合题意要舍去),
不存在正n边形使得∠α=21°.
17.解:(1)∵∠1=∠2+∠D=∠B+∠E+∠D,∠1+∠A+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°;
(2)∵∠1=∠2+∠F=∠B+∠E+∠F,∠1+∠A+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°;
(3)根据图中可得出规律∠A+∠B+∠C+∠D+∠E=180°,每截去一个角则会增加180度,
所以当截去5个角时增加了180×5度,
则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=1080°.
