2020-2021学年初中数学人教版七年级下册7.2坐标方法的简单运用同步练习(word版含答案)
文档属性
| 名称 | 2020-2021学年初中数学人教版七年级下册7.2坐标方法的简单运用同步练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 310.7KB | ||
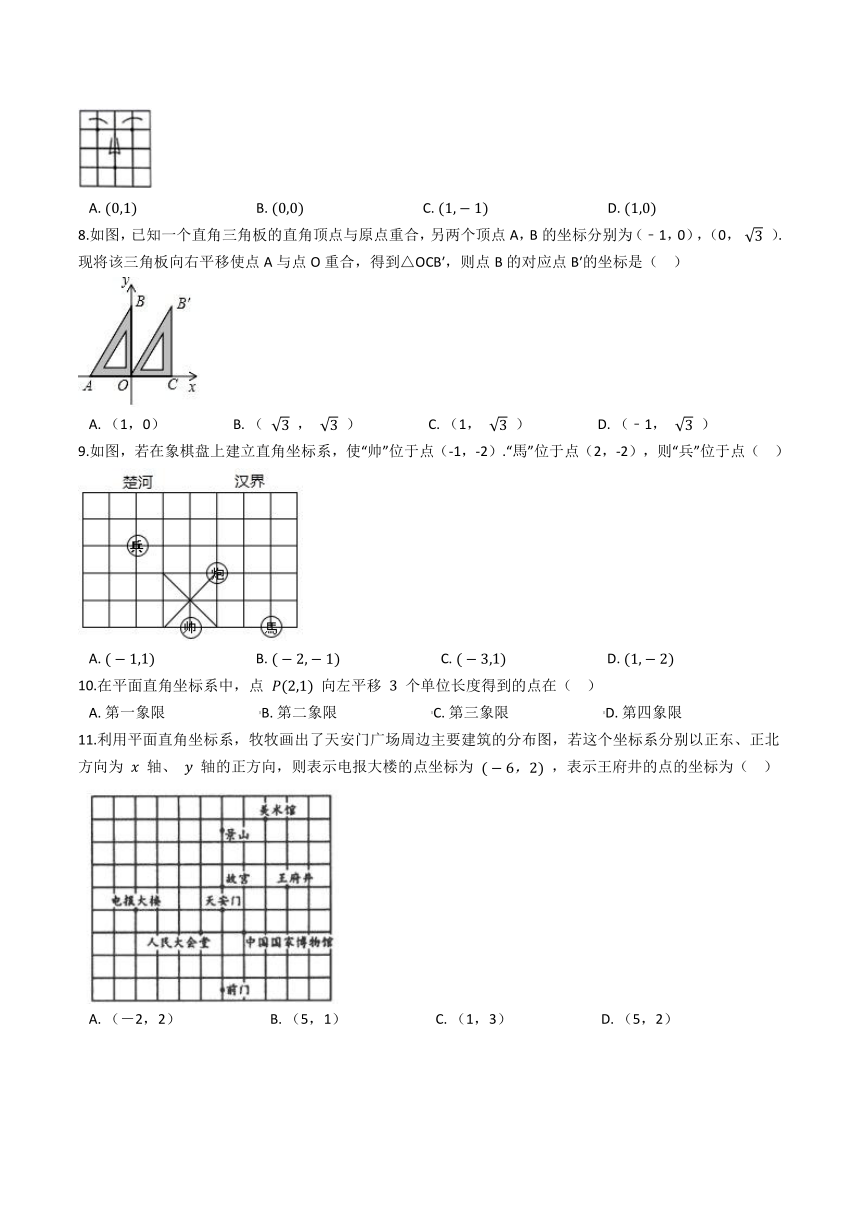
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览


文档简介
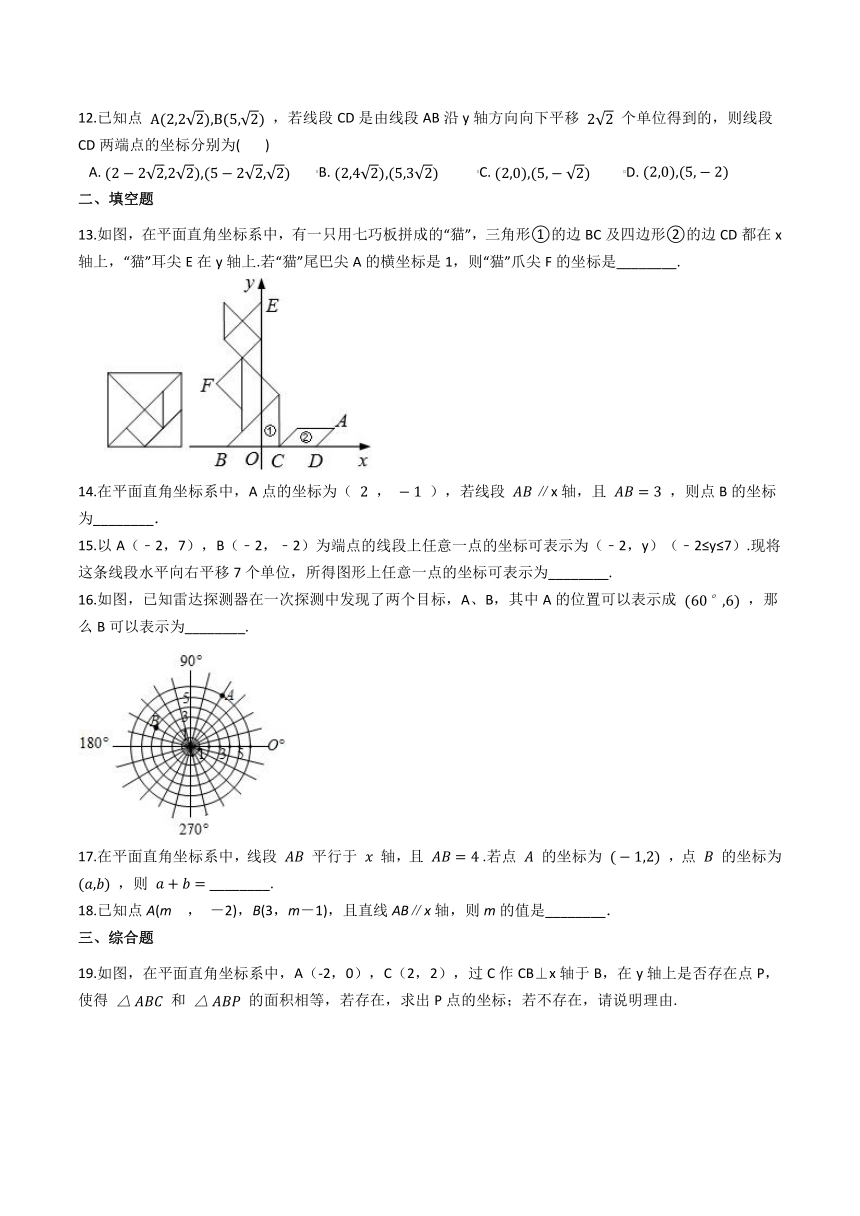
1174750010439400
2020-2021学年初中数学人教版七年级下册第七章平面直角坐标系7.2坐标方法的简单运用同步练习
一、单选题)
1.如图,若A、B两点的坐标分别为(﹣3,5)、(3,5),则点C坐标为( ?)
A.?(﹣2,6)??????????????????????B.?(﹣1,6)??????????????????????C.?(﹣2,7)??????????????????????D.?(﹣1,7)
2.过点 A(?3,?2) 和 B(?3,?5) 作直线,则直线 AB (?? )
A.?与 x 轴平行?????????????????B.?与 y 轴平行?????????????????C.?与 y 轴相交?????????????????D.?与 x 轴, y 轴均相交
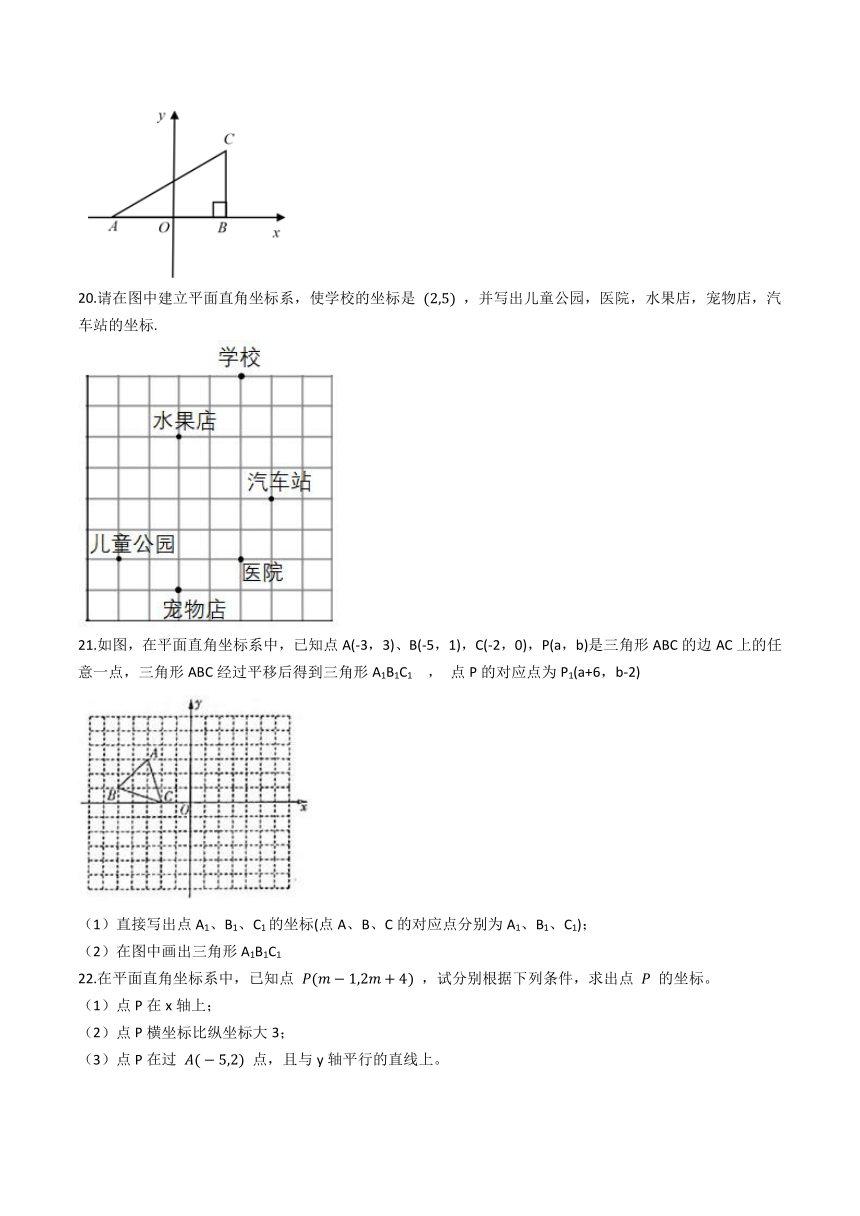
3.若点A的坐标是 (2,?1) ,AB=4,且AB平行于y轴,则点B的坐标为(? )
A.?(2,?5)???????????????????B.?(6,?1) 或 (?2,?1)???????????????????C.?(2,3)???????????????????D.?(2,3) 或 (2,?5)
4.重庆一中寄宿学校北楼,食堂,含弘楼的位置如图所示,如果北楼的位置用(-1,2)表示, 食堂的位置用(2,1)表示,那么含弘楼的位置表示成(?? )
A.?(0,0)???????????????????????????B.?(0,4)???????????????????????????C.?(-2,0)???????????????????????????D.?(1,5)
5.点A在数轴上距原点5个单位长度,将A点先向左移动2个单位长度,再向右移动6个单位长度,此时A点所表示的数是(?? )
A.?-1???????????????????????????????????????B.?9???????????????????????????????????????C.?-1或9???????????????????????????????????????D.?1或9
6.在平面直角坐标系中,点 P(?2,3) 先向左平移 3 个单位,再向下平移 2 个单位,得到的(?? )
A.?(?4,1)???????????????????????????????B.?(?4,5)???????????????????????????????C.?(?5,1)???????????????????????????????D.?(1,1)
7.如图中的一张脸,小明说:“如果我用 (0,2) 表示左眼,用 (2,2) )表示右眼”,那么嘴的位置可以表示成(?? )
A.?(0,1)??????????????????????????????????B.?(0,0)??????????????????????????????????C.?(1,?1)??????????????????????????????????D.?(1,0)
8.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(﹣1,0),(0, 3 ).现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是(?? )
A.?(1,0)???????????????????B.?( 3 , 3 )???????????????????C.?(1, 3 )???????????????????D.?(﹣1, 3 )
9.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2).“馬”位于点(2,-2),则“兵”位于点(?? )
A.?(?1,1)?????????????????????????????B.?(?2,?1)?????????????????????????????C.?(?3,1)?????????????????????????????D.?(1,?2)
10.在平面直角坐标系中,点 P(2,1) 向左平移 3 个单位长度得到的点在(?? )
A.?第一象限???????????????????????????B.?第二象限???????????????????????????C.?第三象限???????????????????????????D.?第四象限
11.利用平面直角坐标系,牧牧画出了天安门广场周边主要建筑的分布图,若这个坐标系分别以正东、正北方向为 x 轴、 y 轴的正方向,则表示电报大楼的点坐标为 (?6,2) ,表示王府井的点的坐标为(?? )
A.?(-2,2)??????????????????????????B.?(5,1)??????????????????????????C.?(1,3)??????????????????????????D.?(5,2)
12.已知点 A(2,22),B(5,2) ,若线段CD是由线段AB沿y轴方向向下平移 22 个单位得到的,则线段CD两端点的坐标分别为(????? )
A.?(2?22,22),(5?22,2)?? ???B.?(2,42),(5,32) ??C.?(2,0),(5,?2)?? ???D.?(2,0),(5,?2)
二、填空题
13.如图,在平面直角坐标系中,有一只用七巧板拼成的“猫”,三角形①的边BC及四边形②的边CD都在x轴上,“猫”耳尖E在y轴上.若“猫”尾巴尖A的横坐标是1,则“猫”爪尖F的坐标是________.
14.在平面直角坐标系中,A点的坐标为( 2 , ?1 ),若线段 AB ∥x轴,且 AB=3 ,则点B的坐标为________.
15.以A(﹣2,7),B(﹣2,﹣2)为端点的线段上任意一点的坐标可表示为(﹣2,y)(﹣2≤y≤7).现将这条线段水平向右平移7个单位,所得图形上任意一点的坐标可表示为________.
16.如图,已知雷达探测器在一次探测中发现了两个目标,A、B,其中A的位置可以表示成 (60°,6) ,那么B可以表示为________.
17.在平面直角坐标系中,线段 AB 平行于 x 轴,且 AB=4 .若点 A 的坐标为 (?1,2) ,点 B 的坐标为 (a,b) ,则 a+b= ________.
18.已知点A(m , -2),B(3,m-1),且直线AB∥x轴,则m的值是________.
三、综合题
19.如图,在平面直角坐标系中,A(-2,0),C(2,2),过C作CB⊥x轴于B,在y轴上是否存在点P,使得 △ABC 和 △ABP 的面积相等,若存在,求出P点的坐标;若不存在,请说明理由.
?
20.请在图中建立平面直角坐标系,使学校的坐标是 (2,5) ,并写出儿童公园,医院,水果店,宠物店,汽车站的坐标.
21.如图,在平面直角坐标系中,已知点A(-3,3)、B(-5,1),C(-2,0),P(a,b)是三角形ABC的边AC上的任意一点,三角形ABC经过平移后得到三角形A1B1C1 , 点P的对应点为P1(a+6,b-2)
(1)直接写出点A1、B1、C1的坐标(点A、B、C的对应点分别为A1、B1、C1);
(2)在图中画出三角形A1B1C1
22.在平面直角坐标系中,已知点 P(m?1,2m+4) ,试分别根据下列条件,求出点 P 的坐标。
(1)点P在x轴上;
(2)点P横坐标比纵坐标大3;
(3)点P在过 A(?5,2) 点,且与y轴平行的直线上。
答案解析部分
一、单选题
1.【答案】 D
【解析】【解答】如图所示,
∵A、B两点的坐标分别为(﹣3,5)、(3,5),
∴则点C坐标为(﹣1,7),
故答案为:D.
【分析】根据A、B的坐标判断出y轴在AB的垂直平分线上,结合图形可得点C的纵坐标比A、B的纵坐标大2,然后解答即可.
2.【答案】 B
【解析】【解答】解:∵A(-3,2)、B(-3,5),
∴横坐标相等,纵坐标不相等,则过A,B两点所在直线平行于y轴,
故答案为:B.
【分析】根据直线平行于y轴的特点:横坐标相等,纵坐标不相等进行解答.
3.【答案】 D
【解析】【解答】∵点A的坐标是 (2,?1) ,AB平行于y轴,
∴点B的横坐标为2,
∵AB=4,
∴当点B在点A上方时,点B的纵坐标为﹣1+4=3,
当点B在点A下方时,点B的纵坐标为﹣1﹣4=﹣5,
∴点B的坐标为 (2,3) 或 (2,?5) ,
故答案为:D.
【分析】根据题意,点B与点A的横坐标相同,纵坐标有两种情况:B在A上方和B在A下方,分别求解即可.
4.【答案】 C
【解析】【解答】由题意,坐标系的位置如图,
所以含弘楼的位置坐标为(-2,0)
故答案为:C.
【分析】根据北楼的坐标(-1,2),向右平移1个单位,再向下平移2个单位即为原点,从而得到坐标系,再根据含弘楼的位置写出坐标即可.
5.【答案】 C
【解析】【解答】解:∵点A在数轴上距原点5个单位长度,
∴点A表示的数是?5或5,
∵A点先向左移动2个单位长度,再向右移动6个单位长度,
∴?5?2+6=?1或5?2+6=9,
∴此时点A所表示的数是?1或9.
故答案为:C.
【分析】分点A在原点左边和右边两种情况,根据向左移动减,向右移动加列式计算即可得解.
6.【答案】 C
【解析】【解答】将点P(-2,3)先向左平移3个单位,再向下平移2个单位,
得到点的坐标是(-2-3,3-2),
即(-5,1),
故答案为:C.
【分析】根据题意,将点P进行按照“左加右减、上加下减”的规则进行平移,即可得到移动后点的坐标。
7.【答案】 D
【解析】【解答】解:根据 (0,2) 表示左眼,用 (2,2) )表示右眼可以确定坐标系如图,
所以嘴的位置可以表示成(1,0).
故答案为:D.
【分析】根据已知条件中的左右两眼的坐标可建立平面直角坐标系,结合嘴所在的位置可求解.
8.【答案】 C
【解析】【解答】解:因为点A与点O对应,点A(﹣1,0),点O(0,0),
所以图形向右平移1个单位长度,
所以点B的对应点B'的坐标为(0+1, 3 ),即(1, 3 ),
故答案为:C.
【分析】利用点的坐标平移规律可得到图形向右平移1个单位长度,根据左减右加,就可得到点B ′ 的坐标。
9.【答案】 C
【解析】【解答】如图,
“兵”位于点(?3,1).
故答案为:C.
【分析】先根据帅的坐标可确定原点的位置,然后可建立平面直角坐标系,再结合兵的位置即可写出坐标.
10.【答案】 B
【解析】【解答】解:点P(2,1)向左平移3个单位后的坐标为(-1,1),
点(-1,1)在第二象限.
故答案为:B.
【分析】求出点P平移后的坐标,继而可判断点P的位置.
11.【答案】 C
【解析】【解答】解:根据题意可建立如下坐标系
如图所示,表示王府井的点的坐标为(1,3)
故答案为:C
【分析】根据表示电报大楼的点坐标为?(?6,2)?,再结合平面直角坐标系求点的坐标即可。
12.【答案】 C
【解析】【解答】解:点 A(2,22) , B(5,2) ,线段 AB 沿 y 轴方向向下平移 22 个单位,即把各点的纵坐标都减 22 ,即可得到线段 CD 两端点的坐标.
则 C(2,0) , D(5,?2) .
故答案为:C.
【分析】根据点坐标平移的特征:左减右加,上加下减求解即可。
二、填空题
13.【答案】 (?1+24,2+24)
【解析】【解答】设大正方形的边长为2a,则大等腰直角三角形的腰长为 2a ,中等腰直角三角形的腰长为a,小等腰直角三角形的腰长为 2a2 ,小正方形的边长为 2a2 ,平行四边形的长边为a,短边为 2a2 ,如图,过点F作FG⊥x轴,垂足为G, 点F作FH⊥y轴,垂足为H, 过点A作AQ⊥x轴,垂足为Q,延长大等腰直角三角形的斜边交x轴于点N,交FH于点M,
根据题意,得OC= 2a22 = 12a ,CD=a,DQ= 12a ,
∵点A的横坐标为1,
∴ 12a +a+ 12a =1,
∴a= 12 ;
根据题意,得FM=PM= 2a2 ,MH= 12a ,
∴FH= (2+1)a2 = 2+14 ;
∴MT=2a- 2a2 ,BT=2a- 2a ,
∴TN= 2a -a,
∴MN=MT+TN=2a- 2a2 + 2a -a= (2+2)a2 = 2+24 ,
∵点F在第二象限,
∴点F的坐标为(- 2+14 , 2+24 )
故答案为:(- 2+14 , 2+24 ).
【分析】设大正方形的边长为2a,则大等腰直角三角形的腰长为 2a ,中等腰直角三角形的腰长为a,小等腰直角三角形的腰长为 2a2 ,小正方形的边长为 2a2 ,平行四边形的长边为a,短边为 2a2 ,如图,过点F作FG⊥x轴,垂足为G, 点F作FH⊥y轴,垂足为H, 过点A作AQ⊥x轴,垂足为Q,延长大等腰直角三角形的斜边交x轴于点N,交FH于点M,分别表示出OC,CD,DQ的长,根据OC+CD+DQ=1,建立关于a的方程,解方程求出a的值;由此可求出FH的长,再表示出MT,NT的长,根据MN=MT+TN,代入计算求出MN的长;即可得到点F的坐标.
14.【答案】 (5, ?1 )或( ?1 , ?1 )
【解析】【解答】解:∵AB∥x轴,
∴点B纵坐标与点A纵坐标相同,为?1,
∵AB=3,
∴当点B在点A的右边时,点B的横坐标为2+3=5;
当点B在点A的左边时,点B的横坐标为2?3=?1;
∴B点坐标为(5,?1),(?1,?1).
故答案为:(5,?1),(?1,?1).
【分析】由AB∥x轴,可得点B纵坐标与点A纵坐标相同,由于AB=3,所以分两种情况:当点B在点A的右边时,当点B在点A的左边时,据此分别求出点B的横坐标,即得结论.
15.【答案】 (5,y) (﹣2≤y≤7)
【解析】【解答】解:A(﹣2,7),B(﹣2,﹣2)向右平移7个单位可得 A1(5,7) , B1(5,?2) ,
∴所得图形上任意一点的坐标可表示 (5,y) (﹣2≤y≤7).
故答案为: (5,y) (﹣2≤y≤7).
【分析】根据平移的特点可知,向右平移横坐标变化,纵坐标不变可得解.
16.【答案】 (150°,4)
【解析】【解答】解:∵(a,b)中,b表示目标与探测器的距离;a表示以正东为始边,逆时针旋转后的角度,
A的位置可以表示成(60°,6),
∴B可以表示为 (150°,4).
故答案为: (150°,4)???.
【分析】按已知可得,表示一个点,距离是自内向外的环数,角度是所在列的度数,据此进行判断即可得解.
17.【答案】 5或-3
【解析】【解答】解:∵点A的坐标是(-1,2),线段AB平行于x轴,
∴点B的纵坐标为 b=2 ;
∵AB=4,
∴ |a?(?1)|=4 ,
∴ a+1=±4 ,
解得: a=3 或 ?5 ,
当 a=3 、 b=2 时, a+b=5 ,
当 a=?5 、 b=2 时, a+b=?3 ,
故答案为:5或-3.
【分析】先根据平行于x轴的直线上的点的纵坐标相等,求出点B的纵坐标 b的值,再根据AB=4,利用两点间的距离得出|a?(?1)|=4 ,解出a值即可.
18.【答案】 -1
【解析】【解答】∵点A(m,-2),B(3,m-1),直线AB∥x轴,
∴m-1=-2,
解得m=-1.
【分析】根据平行于x轴的直线上点的纵坐标相同,列出方程求解即可.
三、解答题
19.【答案】 解:由题意,设点P的坐标为 P(0,a) ,则 OP=|a| ,
∵A(?2,0),C(2,2) ,
∴AB=2?(?2)=4,BC=2 ,
∵CB⊥x 轴,
∴△ABC 的面积为 12AB?BC=12×4×2=4 ,
∵ △ABC 和 △ABP 的面积相等,
∴△ABP 的面积为 12AB?OP=4 ,即 12×4|a|=4 ,
解得 a=±2 ,
故点P的坐标为 P(0,2) 或 P(0,?2) .
【解析】【分析】先根据点A、C的坐标可得AB、BC的长,从而可得 △ABC 的面积,再根据三角形的面积公式可求出OP的长,由此即可得出答案.
20.【答案】 解:如图所示:建立平面直角坐标系,
儿童公园(-2,-1),
医院(2,-1),
水果店(0,3),
宠物店(0,-2),
汽车站(3,1).
【解析】【分析】直接利用学校的坐标是 (2,5) ,得出原点位置进而得出答案.
四、综合题
21.【答案】 (1)解:A1(3,1),B1(1,-1),C1(4,-2)
(2)解:三角形A1B1C1如图所示
【解析】【分析】(1)根据点P和点P对应点的坐标,即可得到平移的规律,继而得到三角形三个顶点平移后的点的坐标即可;
(2)根据平移后的三角形三个顶点的坐标,作出图形即可。
22.【答案】 (1)解:∵点P在x轴上,
∴令2m+4=0,解得m=-2,
则 P点的坐标为(-3,0);
(2)解:∵点 P 横坐标比纵坐标大3,
∴令m-1-(2m+4)=3,解得m=-8,
则P点的坐标为(-9,-12);
(3)解:∵点P在过 A(?5,2) 点,且与y轴平行的直线上,
∴令m-1=-5,解得m=-4.
则 P点的坐标为(-5,-4).
【解析】【分析】(1)让纵坐标为0求得m的值,代入点P的坐标即可求解;
(2)让横坐标-纵坐标=3得m的值,代入点P的坐标即可求解;
(3)让横坐标为-5求得m的值,代入点P的坐标即可求解.
2020-2021学年初中数学人教版七年级下册第七章平面直角坐标系7.2坐标方法的简单运用同步练习
一、单选题)
1.如图,若A、B两点的坐标分别为(﹣3,5)、(3,5),则点C坐标为( ?)
A.?(﹣2,6)??????????????????????B.?(﹣1,6)??????????????????????C.?(﹣2,7)??????????????????????D.?(﹣1,7)
2.过点 A(?3,?2) 和 B(?3,?5) 作直线,则直线 AB (?? )
A.?与 x 轴平行?????????????????B.?与 y 轴平行?????????????????C.?与 y 轴相交?????????????????D.?与 x 轴, y 轴均相交
3.若点A的坐标是 (2,?1) ,AB=4,且AB平行于y轴,则点B的坐标为(? )
A.?(2,?5)???????????????????B.?(6,?1) 或 (?2,?1)???????????????????C.?(2,3)???????????????????D.?(2,3) 或 (2,?5)
4.重庆一中寄宿学校北楼,食堂,含弘楼的位置如图所示,如果北楼的位置用(-1,2)表示, 食堂的位置用(2,1)表示,那么含弘楼的位置表示成(?? )
A.?(0,0)???????????????????????????B.?(0,4)???????????????????????????C.?(-2,0)???????????????????????????D.?(1,5)
5.点A在数轴上距原点5个单位长度,将A点先向左移动2个单位长度,再向右移动6个单位长度,此时A点所表示的数是(?? )
A.?-1???????????????????????????????????????B.?9???????????????????????????????????????C.?-1或9???????????????????????????????????????D.?1或9
6.在平面直角坐标系中,点 P(?2,3) 先向左平移 3 个单位,再向下平移 2 个单位,得到的(?? )
A.?(?4,1)???????????????????????????????B.?(?4,5)???????????????????????????????C.?(?5,1)???????????????????????????????D.?(1,1)
7.如图中的一张脸,小明说:“如果我用 (0,2) 表示左眼,用 (2,2) )表示右眼”,那么嘴的位置可以表示成(?? )
A.?(0,1)??????????????????????????????????B.?(0,0)??????????????????????????????????C.?(1,?1)??????????????????????????????????D.?(1,0)
8.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(﹣1,0),(0, 3 ).现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是(?? )
A.?(1,0)???????????????????B.?( 3 , 3 )???????????????????C.?(1, 3 )???????????????????D.?(﹣1, 3 )
9.如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2).“馬”位于点(2,-2),则“兵”位于点(?? )
A.?(?1,1)?????????????????????????????B.?(?2,?1)?????????????????????????????C.?(?3,1)?????????????????????????????D.?(1,?2)
10.在平面直角坐标系中,点 P(2,1) 向左平移 3 个单位长度得到的点在(?? )
A.?第一象限???????????????????????????B.?第二象限???????????????????????????C.?第三象限???????????????????????????D.?第四象限
11.利用平面直角坐标系,牧牧画出了天安门广场周边主要建筑的分布图,若这个坐标系分别以正东、正北方向为 x 轴、 y 轴的正方向,则表示电报大楼的点坐标为 (?6,2) ,表示王府井的点的坐标为(?? )
A.?(-2,2)??????????????????????????B.?(5,1)??????????????????????????C.?(1,3)??????????????????????????D.?(5,2)
12.已知点 A(2,22),B(5,2) ,若线段CD是由线段AB沿y轴方向向下平移 22 个单位得到的,则线段CD两端点的坐标分别为(????? )
A.?(2?22,22),(5?22,2)?? ???B.?(2,42),(5,32) ??C.?(2,0),(5,?2)?? ???D.?(2,0),(5,?2)
二、填空题
13.如图,在平面直角坐标系中,有一只用七巧板拼成的“猫”,三角形①的边BC及四边形②的边CD都在x轴上,“猫”耳尖E在y轴上.若“猫”尾巴尖A的横坐标是1,则“猫”爪尖F的坐标是________.
14.在平面直角坐标系中,A点的坐标为( 2 , ?1 ),若线段 AB ∥x轴,且 AB=3 ,则点B的坐标为________.
15.以A(﹣2,7),B(﹣2,﹣2)为端点的线段上任意一点的坐标可表示为(﹣2,y)(﹣2≤y≤7).现将这条线段水平向右平移7个单位,所得图形上任意一点的坐标可表示为________.
16.如图,已知雷达探测器在一次探测中发现了两个目标,A、B,其中A的位置可以表示成 (60°,6) ,那么B可以表示为________.
17.在平面直角坐标系中,线段 AB 平行于 x 轴,且 AB=4 .若点 A 的坐标为 (?1,2) ,点 B 的坐标为 (a,b) ,则 a+b= ________.
18.已知点A(m , -2),B(3,m-1),且直线AB∥x轴,则m的值是________.
三、综合题
19.如图,在平面直角坐标系中,A(-2,0),C(2,2),过C作CB⊥x轴于B,在y轴上是否存在点P,使得 △ABC 和 △ABP 的面积相等,若存在,求出P点的坐标;若不存在,请说明理由.
?
20.请在图中建立平面直角坐标系,使学校的坐标是 (2,5) ,并写出儿童公园,医院,水果店,宠物店,汽车站的坐标.
21.如图,在平面直角坐标系中,已知点A(-3,3)、B(-5,1),C(-2,0),P(a,b)是三角形ABC的边AC上的任意一点,三角形ABC经过平移后得到三角形A1B1C1 , 点P的对应点为P1(a+6,b-2)
(1)直接写出点A1、B1、C1的坐标(点A、B、C的对应点分别为A1、B1、C1);
(2)在图中画出三角形A1B1C1
22.在平面直角坐标系中,已知点 P(m?1,2m+4) ,试分别根据下列条件,求出点 P 的坐标。
(1)点P在x轴上;
(2)点P横坐标比纵坐标大3;
(3)点P在过 A(?5,2) 点,且与y轴平行的直线上。
答案解析部分
一、单选题
1.【答案】 D
【解析】【解答】如图所示,
∵A、B两点的坐标分别为(﹣3,5)、(3,5),
∴则点C坐标为(﹣1,7),
故答案为:D.
【分析】根据A、B的坐标判断出y轴在AB的垂直平分线上,结合图形可得点C的纵坐标比A、B的纵坐标大2,然后解答即可.
2.【答案】 B
【解析】【解答】解:∵A(-3,2)、B(-3,5),
∴横坐标相等,纵坐标不相等,则过A,B两点所在直线平行于y轴,
故答案为:B.
【分析】根据直线平行于y轴的特点:横坐标相等,纵坐标不相等进行解答.
3.【答案】 D
【解析】【解答】∵点A的坐标是 (2,?1) ,AB平行于y轴,
∴点B的横坐标为2,
∵AB=4,
∴当点B在点A上方时,点B的纵坐标为﹣1+4=3,
当点B在点A下方时,点B的纵坐标为﹣1﹣4=﹣5,
∴点B的坐标为 (2,3) 或 (2,?5) ,
故答案为:D.
【分析】根据题意,点B与点A的横坐标相同,纵坐标有两种情况:B在A上方和B在A下方,分别求解即可.
4.【答案】 C
【解析】【解答】由题意,坐标系的位置如图,
所以含弘楼的位置坐标为(-2,0)
故答案为:C.
【分析】根据北楼的坐标(-1,2),向右平移1个单位,再向下平移2个单位即为原点,从而得到坐标系,再根据含弘楼的位置写出坐标即可.
5.【答案】 C
【解析】【解答】解:∵点A在数轴上距原点5个单位长度,
∴点A表示的数是?5或5,
∵A点先向左移动2个单位长度,再向右移动6个单位长度,
∴?5?2+6=?1或5?2+6=9,
∴此时点A所表示的数是?1或9.
故答案为:C.
【分析】分点A在原点左边和右边两种情况,根据向左移动减,向右移动加列式计算即可得解.
6.【答案】 C
【解析】【解答】将点P(-2,3)先向左平移3个单位,再向下平移2个单位,
得到点的坐标是(-2-3,3-2),
即(-5,1),
故答案为:C.
【分析】根据题意,将点P进行按照“左加右减、上加下减”的规则进行平移,即可得到移动后点的坐标。
7.【答案】 D
【解析】【解答】解:根据 (0,2) 表示左眼,用 (2,2) )表示右眼可以确定坐标系如图,
所以嘴的位置可以表示成(1,0).
故答案为:D.
【分析】根据已知条件中的左右两眼的坐标可建立平面直角坐标系,结合嘴所在的位置可求解.
8.【答案】 C
【解析】【解答】解:因为点A与点O对应,点A(﹣1,0),点O(0,0),
所以图形向右平移1个单位长度,
所以点B的对应点B'的坐标为(0+1, 3 ),即(1, 3 ),
故答案为:C.
【分析】利用点的坐标平移规律可得到图形向右平移1个单位长度,根据左减右加,就可得到点B ′ 的坐标。
9.【答案】 C
【解析】【解答】如图,
“兵”位于点(?3,1).
故答案为:C.
【分析】先根据帅的坐标可确定原点的位置,然后可建立平面直角坐标系,再结合兵的位置即可写出坐标.
10.【答案】 B
【解析】【解答】解:点P(2,1)向左平移3个单位后的坐标为(-1,1),
点(-1,1)在第二象限.
故答案为:B.
【分析】求出点P平移后的坐标,继而可判断点P的位置.
11.【答案】 C
【解析】【解答】解:根据题意可建立如下坐标系
如图所示,表示王府井的点的坐标为(1,3)
故答案为:C
【分析】根据表示电报大楼的点坐标为?(?6,2)?,再结合平面直角坐标系求点的坐标即可。
12.【答案】 C
【解析】【解答】解:点 A(2,22) , B(5,2) ,线段 AB 沿 y 轴方向向下平移 22 个单位,即把各点的纵坐标都减 22 ,即可得到线段 CD 两端点的坐标.
则 C(2,0) , D(5,?2) .
故答案为:C.
【分析】根据点坐标平移的特征:左减右加,上加下减求解即可。
二、填空题
13.【答案】 (?1+24,2+24)
【解析】【解答】设大正方形的边长为2a,则大等腰直角三角形的腰长为 2a ,中等腰直角三角形的腰长为a,小等腰直角三角形的腰长为 2a2 ,小正方形的边长为 2a2 ,平行四边形的长边为a,短边为 2a2 ,如图,过点F作FG⊥x轴,垂足为G, 点F作FH⊥y轴,垂足为H, 过点A作AQ⊥x轴,垂足为Q,延长大等腰直角三角形的斜边交x轴于点N,交FH于点M,
根据题意,得OC= 2a22 = 12a ,CD=a,DQ= 12a ,
∵点A的横坐标为1,
∴ 12a +a+ 12a =1,
∴a= 12 ;
根据题意,得FM=PM= 2a2 ,MH= 12a ,
∴FH= (2+1)a2 = 2+14 ;
∴MT=2a- 2a2 ,BT=2a- 2a ,
∴TN= 2a -a,
∴MN=MT+TN=2a- 2a2 + 2a -a= (2+2)a2 = 2+24 ,
∵点F在第二象限,
∴点F的坐标为(- 2+14 , 2+24 )
故答案为:(- 2+14 , 2+24 ).
【分析】设大正方形的边长为2a,则大等腰直角三角形的腰长为 2a ,中等腰直角三角形的腰长为a,小等腰直角三角形的腰长为 2a2 ,小正方形的边长为 2a2 ,平行四边形的长边为a,短边为 2a2 ,如图,过点F作FG⊥x轴,垂足为G, 点F作FH⊥y轴,垂足为H, 过点A作AQ⊥x轴,垂足为Q,延长大等腰直角三角形的斜边交x轴于点N,交FH于点M,分别表示出OC,CD,DQ的长,根据OC+CD+DQ=1,建立关于a的方程,解方程求出a的值;由此可求出FH的长,再表示出MT,NT的长,根据MN=MT+TN,代入计算求出MN的长;即可得到点F的坐标.
14.【答案】 (5, ?1 )或( ?1 , ?1 )
【解析】【解答】解:∵AB∥x轴,
∴点B纵坐标与点A纵坐标相同,为?1,
∵AB=3,
∴当点B在点A的右边时,点B的横坐标为2+3=5;
当点B在点A的左边时,点B的横坐标为2?3=?1;
∴B点坐标为(5,?1),(?1,?1).
故答案为:(5,?1),(?1,?1).
【分析】由AB∥x轴,可得点B纵坐标与点A纵坐标相同,由于AB=3,所以分两种情况:当点B在点A的右边时,当点B在点A的左边时,据此分别求出点B的横坐标,即得结论.
15.【答案】 (5,y) (﹣2≤y≤7)
【解析】【解答】解:A(﹣2,7),B(﹣2,﹣2)向右平移7个单位可得 A1(5,7) , B1(5,?2) ,
∴所得图形上任意一点的坐标可表示 (5,y) (﹣2≤y≤7).
故答案为: (5,y) (﹣2≤y≤7).
【分析】根据平移的特点可知,向右平移横坐标变化,纵坐标不变可得解.
16.【答案】 (150°,4)
【解析】【解答】解:∵(a,b)中,b表示目标与探测器的距离;a表示以正东为始边,逆时针旋转后的角度,
A的位置可以表示成(60°,6),
∴B可以表示为 (150°,4).
故答案为: (150°,4)???.
【分析】按已知可得,表示一个点,距离是自内向外的环数,角度是所在列的度数,据此进行判断即可得解.
17.【答案】 5或-3
【解析】【解答】解:∵点A的坐标是(-1,2),线段AB平行于x轴,
∴点B的纵坐标为 b=2 ;
∵AB=4,
∴ |a?(?1)|=4 ,
∴ a+1=±4 ,
解得: a=3 或 ?5 ,
当 a=3 、 b=2 时, a+b=5 ,
当 a=?5 、 b=2 时, a+b=?3 ,
故答案为:5或-3.
【分析】先根据平行于x轴的直线上的点的纵坐标相等,求出点B的纵坐标 b的值,再根据AB=4,利用两点间的距离得出|a?(?1)|=4 ,解出a值即可.
18.【答案】 -1
【解析】【解答】∵点A(m,-2),B(3,m-1),直线AB∥x轴,
∴m-1=-2,
解得m=-1.
【分析】根据平行于x轴的直线上点的纵坐标相同,列出方程求解即可.
三、解答题
19.【答案】 解:由题意,设点P的坐标为 P(0,a) ,则 OP=|a| ,
∵A(?2,0),C(2,2) ,
∴AB=2?(?2)=4,BC=2 ,
∵CB⊥x 轴,
∴△ABC 的面积为 12AB?BC=12×4×2=4 ,
∵ △ABC 和 △ABP 的面积相等,
∴△ABP 的面积为 12AB?OP=4 ,即 12×4|a|=4 ,
解得 a=±2 ,
故点P的坐标为 P(0,2) 或 P(0,?2) .
【解析】【分析】先根据点A、C的坐标可得AB、BC的长,从而可得 △ABC 的面积,再根据三角形的面积公式可求出OP的长,由此即可得出答案.
20.【答案】 解:如图所示:建立平面直角坐标系,
儿童公园(-2,-1),
医院(2,-1),
水果店(0,3),
宠物店(0,-2),
汽车站(3,1).
【解析】【分析】直接利用学校的坐标是 (2,5) ,得出原点位置进而得出答案.
四、综合题
21.【答案】 (1)解:A1(3,1),B1(1,-1),C1(4,-2)
(2)解:三角形A1B1C1如图所示
【解析】【分析】(1)根据点P和点P对应点的坐标,即可得到平移的规律,继而得到三角形三个顶点平移后的点的坐标即可;
(2)根据平移后的三角形三个顶点的坐标,作出图形即可。
22.【答案】 (1)解:∵点P在x轴上,
∴令2m+4=0,解得m=-2,
则 P点的坐标为(-3,0);
(2)解:∵点 P 横坐标比纵坐标大3,
∴令m-1-(2m+4)=3,解得m=-8,
则P点的坐标为(-9,-12);
(3)解:∵点P在过 A(?5,2) 点,且与y轴平行的直线上,
∴令m-1=-5,解得m=-4.
则 P点的坐标为(-5,-4).
【解析】【分析】(1)让纵坐标为0求得m的值,代入点P的坐标即可求解;
(2)让横坐标-纵坐标=3得m的值,代入点P的坐标即可求解;
(3)让横坐标为-5求得m的值,代入点P的坐标即可求解.
