2021-2022学年人教版九年级上册22.2 二次函数与系数的关系练习(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级上册22.2 二次函数与系数的关系练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 100.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览




文档简介
117348001267460022.2 二次函数与系数关系
一、选择题
抛物线y=?x2+4x?4与坐标轴的交点个数为(? ? ? )
A. 0 B. 1 C. 2 D. 3
若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为(????)
A. x1=0,x2=4 B. x1=1,x2=5
C. x1=1,x2=?5 D. x1=?1,x2=5
若二次函数y=kx2?2x?1与x轴有交点,则k的取值范围是(????)
A. k>?1 B. k≤1且k≠0 C. k已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是(????)
A. a+b+c>0
B. a>0
C. b2?4ac<0
D. c<0
对于一个函数,自变量x取c时,函数值y等于0,则称c为这个函数的零点.若关于x的二次函数y=?x2?10x+m(m≠0)有两个不相等的零点x1,x2(x1 A. 01 C. 01
二次函数y=ax2+bx+c(a≠0)的顶点坐标为(?1,n),其部分图象如图所示.以下结论错误的是(????)
A. abc>0
B. 4ac?b2<0
C. 3a+c>0
D. 关于x的方程ax2+bx+c=n+1无实数根
如图所示为二次函数y=ax2+bx+c(a≠0)图象一部分,则以下正确的有:①b>2a;②ax2+bx+c=0的两根分别为?3和1;③a?2b+c<0;④a+b+c=0;⑤8a+c>0,其中正确的有(????)
A. ①②
B. ②③
C. ②③④
D. ②③④⑤
如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(?2,0)、B(1,0)两点.则以下结论:①ac>0;②二次函数y=ax2+bx+c的图象的对称轴为x=?1;③2a+c=0;④a?b+c>0.其中正确的有(????)个.
A. 0 B. 1 C. 2 D. 3
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(?1,0)和B,与y轴交于点C.下列结论:①abc<0,②2a+b<0,③4a?2b+c>0,④3a+c>0,其中正确的结论个数为(????)
A. 1个
B. 2个
C. 3个
D. 4个
已知:抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(?1,0),其部分图象如图所示,下列结论:
①4ac③a?b+c>0;④当y>0时,x的取值范围是?1≤x<3;
⑤当x<0时,y随x增大而增大
其中正确的结论有(????)
A. 4个 B. 3个 C. 2个 D. 1个
二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的部分图象如图所示,图象顶点的坐标为(2,1),与x轴的一个交点在点(3,0)和点(4,0)之间,有下列结论:①abc<0;②a?b+c>0;③c?4a=1;④b2>4ac;⑤am2+bm+c≤1(m为任意实数).其中正确的有(????)
A. 2个 B. 3个 C. 4个 D. 5个
二次函数y=ax2+bx+c的图象过点(?1,0),对称轴为直线x=2,若a>0,则下列结论错误的是(????)
A. 当x>2时,y随着x的增大而增大
B. (a+c)2=b2
C. 若A(x1,m)、B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c
D. 若方程a(x+1)(5?x)=?1的两根为x1、x2,且x1二次函数y=x2+bx的对称轴为直线x=2,若关于x的一元二次方程x2+bx?t=0(t为实数)在?1 A. 0已知抛物线y=a(x??)2+k与x轴有两个交点A(?1,0),B(3,0),抛物线y=a(x???m)2+k与x轴的一个交点是(4,0),则m的值是(????)
A. 5 B. ?1 C. 5或1 D. ?5或?1
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
①ac>0;②a?b+c<0;③当x<0时,y<0;
④方程ax2+bx+c=0(a≠0)有两个大于?1的实数根.
其中错误的结论有(??? ).
A. ②③ B. ②④ C. ①③ D. ①④
二次函数y=ax2+bx+c的部分图象如图所示,对称轴是直线x=?1.5,与x轴的一个交点在(?4,0)和(?3,0)之间,有以下结论:①abc>0;②b2?4ac>0;③3a?b=0;④4b+3c<0.其中正确结论的个数是(????)
A. 1 B. 2 C. 3 D. 4
如图,抛物线y=?x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个判断:①当x>0时,y>0;②当x>1时,y随x的增大而减少;③m>?1;④当a=?1时,b=3;其中,判断正确的序号是(????)
A. ①② B. ②③ C. ①③ D. ②③④
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(4,0),其对称轴为直线x=1,结合图象,下列结论:
①ac<0;
②4a?2b+c>0;
③当x>2时,y随x的增大而增大;
④关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根.
其中正确的结论有(????)
A. ①④
B. ③④
C. ①②④
D. ①③④
已知抛物线y=ax2+bx+c(a≠0)经过点(?1,0),(0,3),对称轴在y轴右侧,则下列结论:①a<0;②抛物线经过(1,0);③方程ax2+bx+c=1有两个不相等的实数根;④?3 A. ①③ B. ①②③ C. ①③④ D. ③④
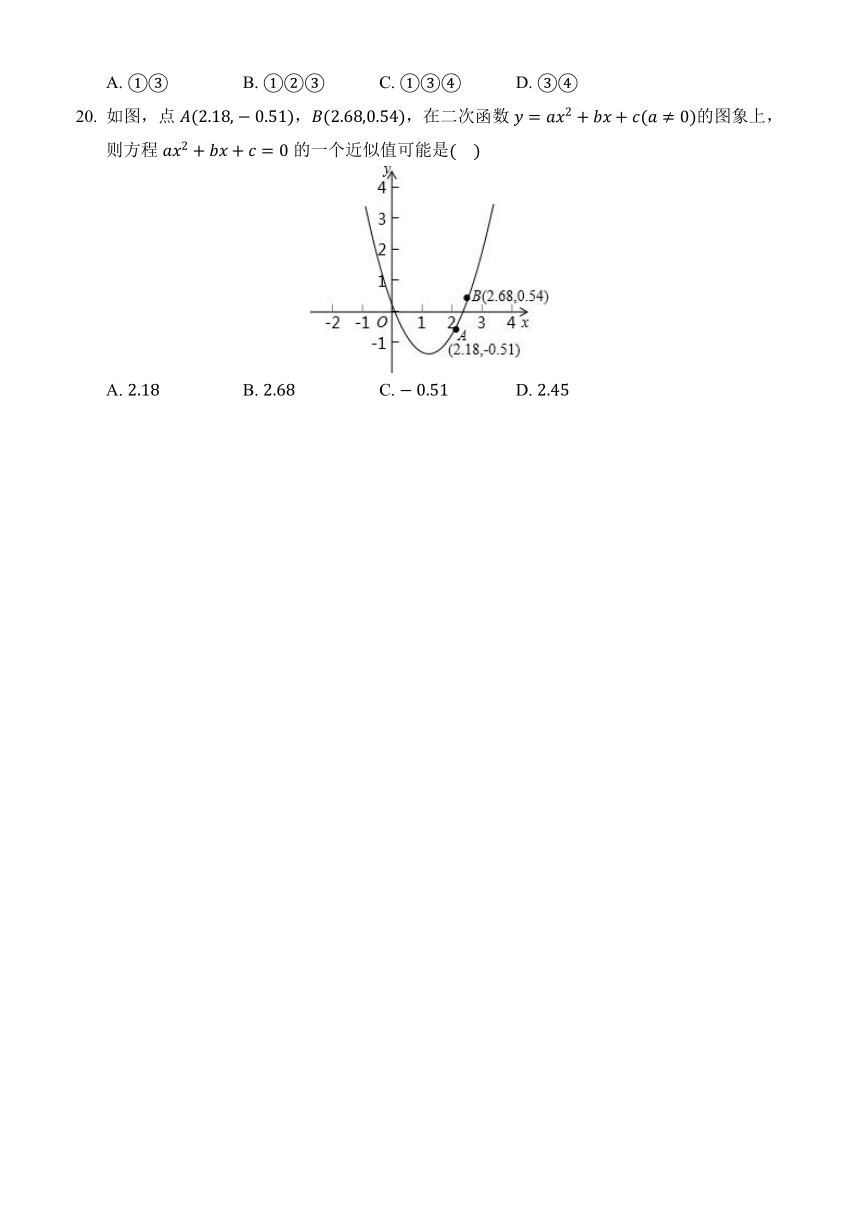
如图,点A(2.18,?0.51),B(2.68,0.54),在二次函数y=ax2+bx+c(a≠0)的图象上,则方程ax2+bx+c=0的一个近似值可能是(????)
A. 2.18 B. 2.68 C. ?0.51 D. 2.45
答案和解析
1.【答案】C
【解析】
【分析】
本题考查了二次函数图象上点的坐标特征,抛物线与x轴的交点,属于中档题.
先计算自变量为0时对应的函数值得到抛物线与y轴的交点坐标;再把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程,解方程?x2+4x?4=0得抛物线与x轴的交点坐标,从而可对各选项进行判断.
【解答】
解:
当x=0时,y=?x2+4x?4=?4,则抛物线与y轴的交点坐标为(0,?4),
当y=0时,?x2+4x?4=0,解得x1=x2=2,抛物线与x轴的交点坐标为(2,0),
所以抛物线与坐标轴有2个交点.
故选C.??
2.【答案】D
【解析】
【分析】本题主要考查二次函数的对称轴和二次函数与一元二次方程的关系,难度不大.
根据对称轴方程?b2=2,得b=?4,解x2?4x=5即可.
【解答】
解由题意知函数图象的对称轴为直线x=2,
根据对称轴方程?b2=2,得b=?4,
代入方程得x2?4x?5=0,
解得x1=?1,x2=5,
故选D.
??
3.【答案】D
【解析】解:∵二次函数y=kx2?2x?l与x轴有交点,
∴△=(?2)2?4k×(?1)≥0,且k≠0,
解得k≥?1且k≠0,
故选:D.
根据二次函数的定义得到k≠0;根据一元二次方程kx2?2x?l=0的根的判别式的符号列出不等式,通过解不等式即可求得k的取值范围.
本题考查了抛物线与x轴的交点,二次函数的定义.注意二次函数解析式与一元二次方程间的关系.
4.【答案】A
【解析】解:A、由图象可知当x=1时,y>0,则a+b+c>0,故此选项正确;
B、由二次函数的图象开口向下可得a<0,故此选项错误;
C、由抛物线与x轴有两个交点可以看出方程ax2+bx+c=0的根的判别式b2?4ac>0,故此选项错误;
D、根据二次函数的图象与y轴交于负半轴知:c<0,故此选项错误;
故选:A.
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点得出c的值,然后根据抛物线与x轴交点的个数及x=1时二次函数的值的情况进行推理,进而对所得结论进行判断.
本题考查了图象与二次函数系数之间的关系,二次函数与方程之间的转换,根的判别式的熟练运用.会利用特殊值代入法求得特殊的式子,如:y=a+b+c,y=a?b+c,然后根据图象判断其值.
5.【答案】A
【解析】
【分析】
本题考查了抛物线与x轴的交点,二次函数图象上点的坐标特征,利用图象判断是解题的关键.
根据题意画出关于x的二次函数y=?x2?10x+m(m≠0)的图象以及直线y=?2,根据图象即可判断.
【解答】
解:由题意关于x的方程x2+10x?m?2=0有两个不相等的非零实数根x3,x4(x3画出函数的图象草图如下:
∵抛物线的对称轴为直线x=??102×(?1)=?5,
∴x3由图象可知:0故选:A.??
6.【答案】C
【解析】解:A.∵抛物线开口向下,
∴a<0,
∵对称轴为直线x=?b2a=?1,
∴b=2a<0,
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc>0,
故A正确;
B.∵抛物线与x轴有两个交点,
∴b2?4ac>0,即4ac?b2<0,
故B正确;
C.∵抛物线的对称轴为直线x=?1,抛物线与x轴的一个交点在(?3,0)和(?2,0)之间,
∴抛物线与x轴的另一个交点在(0,0)和(1,0)之间,
∴x=1时,y<0,
即a+b+c<0,
∵b=2a,
∴3a+c<0,
故C错误;
D.∵抛物线开口向下,顶点为(?1,n),
∴函数有最大值n,
∴抛物线y=ax2+bx+c与直线y=n+1无交点,
∴一元二次方程ax2+bx+c=n+1无实数根,
故D正确.
故选:C.
根据抛物线开口方向,对称轴的位置以及与y轴的交点可以对A进行判断;根据抛物线与x轴的交点情况可对B进行判断;x=1时,y<0,可对C进行判断;根据抛物线y=ax2+bx+c与直线y=n+1无交点,可对D进行判断.
本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质.
7.【答案】D
【解析】解:①∵抛物线的对称轴为直线x=?b2a=?1,
∴b=2a,结论①错误;
②∵抛物线的对称轴为直线x=?1,抛物线与x轴一个交点的坐标为(1,0),
∴抛物线与x轴另一交点的坐标为(?3,0),
∴ax2+bx+c=0的两根分别为?3和1,结论②正确;
③∵抛物线开口向上,与y轴交于负半轴,
∴a>0,c<0,
∴a?2b+c=a?4a+c=?3a+c<0,结论③正确;
④∵当x=1时,y=0,
∴a+b+c=0,结论④正确;
⑤∵当x=2时,y>0,
∴4a+2b+c=8a+c>0,结论⑤正确.
综上所述:正确的结论有②③④⑤.
故选:D.
①由抛物线的对称轴为直线x=?1,可得出b=2a,结论①错误;②由抛物线的对称轴及抛物线与x轴一个交点的坐标,可求出另一交点坐标,进而可得出ax2+bx+c=0的两根分别为?3和1,结论②正确;③由抛物线的开口方向及抛物线与y轴交点的位置可得出a>0,c<0,结合b=2a,即可得出a?2b+c=?3a+c<0,结论③正确;④由当x=1时y=0,可得出a+b+c=0,结论④正确;⑤由当x=2时y>0结合b=2a,可得出4a+2b+c=8a+c>0,结论⑤正确.综上即可得出结论.
本题考查了二次函数图象与系数的关系、二次函数图象上点的坐标特征以及抛物线与x轴的交点,观察函数图象,逐一分析五个结论的正误是解题的关键.
8.【答案】C
【解析】解:对于①:二次函数开口向下,故a<0,与y轴的交点在y的正半轴,故c>0,故ac<0,因此①错误;
对于②:二次函数的图象与x轴相交于A(?2,0)、B(1,0),由对称性可知,其对称轴为:x=?2+12=?12,因此②错误;
对于③:设二次函数y=ax2+bx+c的交点式为y=a(x+2)(x?1)=ax2+ax?2a,比较一般式与交点式的系数可知:b=a,c=?2a,故2a+c=0,因此③正确;
对于④:当x=?1时对应的y=a?b+c,观察图象可知x=?1时对应的函数图象的y值在x轴上方,故a?b+c>0,因此④正确.
∴只有③④是正确的.
故选:C.
根据抛物线的开口方向、对称轴、顶点坐标、增减性以及过特殊点时系数a、b、c满足的关系综合判断即可.
本题考查了二次函数的图象与其系数的关系及二次函数的对称性,熟练掌握二次函数的图象性质是解决此类题的关键.
9.【答案】B
【解析】解:①∵由抛物线的开口向上知a>0,
∵对称轴位于y轴的右侧,
∴b<0.
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc>0;
故错误;
②对称轴为x=?b2a<1,得2a>?b,即2a+b>0,
故错误;
③如图,当x=?2时,y>0,4a?2b+c>0,
故正确;
④∵当x=?1时,y=0,
∴0=a?b+c0.
故正确.
综上所述,有2个结论正确.
故选:B.
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴求出2a与b的关系.
本题主要考查抛物线与x轴的交点坐标,二次函数图象与函数系数之间的关系,解题的关键是掌握数形结合思想的应用,注意掌握二次函数图象与系数的关系.
10.【答案】B
【解析】解:①∵抛物线与x轴有2个交点,
∴b2?4ac>0,即4ac②∵抛物线的对称轴为直线x=1,
而点(?1,0)关于直线x=1的对称点的坐标为(3,0),
∴方程ax2+bx+c=0的两个根是x1=?1,x2=3,所以②正确;
③∵抛物线y=ax2+bx+c(a≠0)经过点(?1,0),
∴a?b+c=0,所以③错误;
④∵抛物线与x轴的两点坐标为(?1,0),(3,0),
∴当?10,所以④错误;
⑤∵抛物线的对称轴为直线x=1,
∴当x<1时,y随x增大而增大,所以⑤正确.
故选B.
利用抛物线与x轴的交点个数可对①进行判断;利用抛物线的对称性得到抛物线与x轴的一个交点坐标为(3,0),则可对②进行判断;根据抛物线过点(?1,0),则可对③进行判断;根据抛物线在x轴上方所对应的自变量的范围可对④进行判断;根据二次函数的性质对⑤进行判断.
本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点位置:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2?4ac>0时,抛物线与x轴有2个交点;△=b2?4ac=0时,抛物线与x轴有1个交点;△=b2?4ac<0时,抛物线与x轴没有交点.
11.【答案】B
【解析】解:由图象可知,抛物线开口向下,对称轴在y轴的右侧,与y轴的交点在y轴的负半轴,
∴a<0,b>0,c<0,
∴abc>0,故①错误;
由图象可知,x=?1时,y<0,
∴a?b+c<0,故②错误;
∵抛物线的顶点坐标为(2,1),
∴?b2a=2,b=?4a,
∵4a+2b+c=1,
∴4a?8a+c=1,即c?4a=1,故③正确;
∵抛物线与x轴有两个交点,
∴△>0,
∴b2?4ac>0,即b2>4ac,故④正确.
∵抛物线的开口向下,顶点坐标为(2,1),
∴am2+bm+c≤1(m为任意实数),故⑤正确.
故选:B.
①抛物线的开口方向,对称轴以及与y轴的交点即可判断;
②根据x=?1时,y<0,即可判断.
③根据对称轴x=?b2a=2,即可判断.
③根据抛物线与x轴有两个交点,可知△>0,即可判断.
④根据抛物线的顶点坐标为(2,1),函数有最大值,由此即可判断.
本题考查二次函数与x轴的交点、二次函数的图象与系数的关系等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
12.【答案】D
【解析】解:∵二次函数y=ax2+bx+c中,a>0,对称轴为直线x=2,
∴当x>2时,y随着x的增大而增大,故A正确;
∵?b2a=2,
∴b=?4a,
∵二次函数y=ax2+bx+c的图象过点(?1,0),
∴a?b+c=0,即a+4a+c=0,
∴c=?5a,
∴a+c=?4a,
∴(a+c)2=b2,故B正确;
∵A(x1,m)、B(x2,m)是抛物线上的两点,
∴抛物线对称轴x=x1+x22,
∴2x=x1+x2,
∵x=x1+x2,
∴2x=x,
∴x=0,
∴此时,y=ax2+bx+c=c,故C正确;
∵抛物线的对称轴为直线x=2,图象与x轴交于(?1,0),
∴抛物线x轴的另一个交点是(5,0),
∴抛物线与直线y=?1的交点横坐标x1>?1,x2<5,如图,
∴方程a(x+1)(x?5)=?1的两根为x1和x2,且x1故选:D.
根据二次函数的性质即可判断A;根据对称轴得到b=?4a,经过点(?1,0)得到c=?5a,从而求得a+c=?4a,即可判断B;由抛物线的对称性得到x=x1+x22,结合x=x1+x2,即可判断C;利用二次函数与一元二次方程的关系即可判断D.
本题考查了二次函数图象与系数的关系,二次函数图象上点的坐标特征,二次函数的性质,抛物线与x轴的交点,熟练掌握二次函数的性质是解题的关键.
13.【答案】B
【解析】解:∵对称轴为直线x=2,
∴b=?4,
∴y=x2?4x,
关于x的一元二次方程x2+bx?t=0的解可以看成二次函数y=x2?4x与直线y=t的交点,
∵?1∴二次函数y的取值为?4≤y<5,
∴?4≤t<5;
故选:B.
先求出b,确定二次函数解析式,关于x的一元二次方程x2+bx?t=0的解可以看成二次函数y=x2?4x与直线y=t的交点,?1本题考查二次函数图象的性质,一元二次方程的解;将一元二次方程的解转换为二次函数与直线交点问题,数形结合的解决问题是解题的关键.
14.【答案】C
【解析】解:∵抛物线y=a(x??)2+k的对称轴为直线x=?,抛物线y=a(x???m)2+k的对称轴为直线x=?+m,
∴当点A(?1,0)平移后的对应点为(4,0),则m=4?(?1)=5;
当点B(3,0)平移后的对应点为(4,0),则m=4?3=1,
即m的值为5或1.
故选:C.
先利用二次函数的性质得到两抛物线的对称轴,然后利用A点或B点向右平移得到点(4,0)得到m的值.
本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质.
15.【答案】C
【解析】
【分析】
此题主要考查了二次函数图像与系数的关系,二次函数性质等内容,解题关键是利用图象求出a,b,c的范围,以及特殊值的代入能得到特殊的式子,如:当x=1时,y>0,a+b+c>0;x=?1时,y<0,a?b+c<0.
①由二次函数y=ax2+bx+c(a≠0)的图象开口方向知道a<0,与y轴交点知道c>0,由此即可确定ac的符号;
②由于当x=?1时,y=a?b+c,而根据图象知道当x=?1时y<0,由此即可判定a?b+c的符号;
③根据图象知道当x<0时,y④根据图象与x轴交点的情况即可判定是否正确.
【解答】
解:∵图象开口向下,∴a<0,
∵图象与y轴交于正半轴,则c>0,
∴ac<0,故选项①错误;
∵当x=?1时,对应y值小于0,即a?b+c<0,故选项②正确;
当x<0时,y利用图象与x轴交点都大于?1,故方程ax2+bx+c=0(a≠0)有两个大于?1的实数根,故选项④正确;
故选;C.??
16.【答案】D
【解析】解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=?b2a=?1.5,
∴b=3a<0,
∴3a?b=0,所以③正确;
∵抛物线交y的正半轴,
∴c>0,
∴abc>0,所以①正确;
∵抛物线与x轴有两个交点,
∴b2?4ac>0,所以②正确;
由图象可知,x=1时y<0,且b=3a,
即a+b+c=13b+b+c=43b+c<0,
即4b+3c<0,故④正确;
故选:D.
根据抛物线开口方向,对称轴以及与y轴的交点即可判断①③;根据抛物线与x轴的交点即可判断②;由图象可知,x=1时y<0,且b=3a,即可得到a+b+c=13b+b+c=43b+c<0,即可判断④.
本题考查了二次函数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右.常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由Δ决定:Δ=b2?4ac>0时,抛物线与x轴有2个交点;Δ=b2?4ac=0时,抛物线与x轴有1个交点;Δ=b2?4ac<0时,抛物线与x轴没有交点.
17.【答案】D
【解析】解:①由图象可知,当x>0时,y可以小于0,故①错误;
②∵抛物线的对称轴为x=?22×(?1)=1,
∴当x>1时,y随x的增大而减少,故②正确;
③由图象可知m+1>0,
∴m>?1,故③正确;
④若a=?1,则A(?1,0),抛物线的对称轴为x=1,
∴B(3,0),
∴b=3,故④正确;
故选:D.
根据函数图象即可判断①;求得对称轴为直线x=1,观察图象即可判断②;由抛物线与y轴的交点即可判断③;根据抛物线的对称性即可判断④.
本题考查了二次函数图象与系数的关系,二次函数的性质,数形结合是解题的关键.
18.【答案】D
【解析】解:抛物线开口向上,因此a>0,与y轴交于负半轴,因此c<0,故ac<0,所以①正确;
抛物线对称轴为x=1,与x轴的一个交点为(4,0),则另一个交点为(?2,0),于是有4a?2b+c=0,所以②不正确;
x>1时,y随x的增大而增大,所以③正确;
抛物线与x轴有两个不同交点,因此关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根,所以④正确;
综上所述,正确的结论有:①③④,
故选:D.
根据抛物线的开口方向、对称轴、顶点坐标、增减性以及与x轴y轴的交点,综合判断即可.
本题考查二次函数的图象和性质,掌握二次函数的图象与系数之间的关系是正确判断的前提.
19.【答案】C
【解析】解:①∵抛物线y=ax2+bx+c(a≠0)经过点(?1,0),(0,3),对称轴在y轴右侧,
∴抛物线开口向下,
∴a<0,结论①正确;
②∵抛物线过点(?1,0),对称轴在y轴右侧,
∴当x=1时y>0,结论②错误;
③∵顶点的纵坐标大于3,
∴过点(0,1)作x轴的平行线与抛物线有两个交点,
∴方程ax2+bx+c=1有两个不相等的实数根,结论③正确;
④∵当x=1时y=a+b+c>0,
∴a+b>?c.
∵抛物线y=ax2+bx+c(a,b,c为常数,a≠0)经过点(0,3),
∴c=3,
∴a+b>?3.
∵当x=?1时,y=0,即a?b+c=0,
∴b=a+c,
∴a+b=2a+c.
∵抛物线开口向下,
∴a<0,
∴a+b∴?3故选:C.
①由抛物线y=ax2+bx+c(a≠0)经过点(?1,0),(0,3),对称轴在y轴右侧,即可判断开口向下,结论①正确;
②由抛物线过点(?1,0),对称轴在y轴右侧,即可得出当x=1时y>0,结论①错误;
②过点(0,1)作x轴的平行线,由该直线与抛物线有两个交点,可得出方程ax2+bx+c=1有两个不相等的实数根,结论③正确;
④由当x=1时y>0,可得出a+b>?c,由抛物线与y轴交于点(0,3)可得出c=3,进而即可得出a+b>?3,由抛物线过点(?1,0)可得出a+b=2a+c,结合a<0、c=3可得出a+b<3,综上可得出?3本题考查了抛物线与x轴的交点、二次函数的性质以及二次函数图象上点的坐标特征,逐一分析三条结论的正误是解题的关键.
20.【答案】D
【解析】解:∵图象上有两点分别为A(2.18,?0.51)、B(2.68,0.54),
∴当x=2.18时,y=?0.51;x=2.68时,y=0.54,
∴当y=0时,2.18只有选项D符合,
故选:D.
根据自变量两个取值所对应的函数值是?0.51和0.54,可得当函数值为0时,x的取值应在所给的自变量两个值之间.
本题考查了图象法求一元二次方程的近似值,用到的知识点为:点在函数解析式上,点的横纵坐标适合这个函数解析式;二次函数值为0,就是函数图象与x轴的交点,跟所给的接近的函数值对应的自变量相关.
一、选择题
抛物线y=?x2+4x?4与坐标轴的交点个数为(? ? ? )
A. 0 B. 1 C. 2 D. 3
若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为(????)
A. x1=0,x2=4 B. x1=1,x2=5
C. x1=1,x2=?5 D. x1=?1,x2=5
若二次函数y=kx2?2x?1与x轴有交点,则k的取值范围是(????)
A. k>?1 B. k≤1且k≠0 C. k已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是(????)
A. a+b+c>0
B. a>0
C. b2?4ac<0
D. c<0
对于一个函数,自变量x取c时,函数值y等于0,则称c为这个函数的零点.若关于x的二次函数y=?x2?10x+m(m≠0)有两个不相等的零点x1,x2(x1
二次函数y=ax2+bx+c(a≠0)的顶点坐标为(?1,n),其部分图象如图所示.以下结论错误的是(????)
A. abc>0
B. 4ac?b2<0
C. 3a+c>0
D. 关于x的方程ax2+bx+c=n+1无实数根
如图所示为二次函数y=ax2+bx+c(a≠0)图象一部分,则以下正确的有:①b>2a;②ax2+bx+c=0的两根分别为?3和1;③a?2b+c<0;④a+b+c=0;⑤8a+c>0,其中正确的有(????)
A. ①②
B. ②③
C. ②③④
D. ②③④⑤
如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(?2,0)、B(1,0)两点.则以下结论:①ac>0;②二次函数y=ax2+bx+c的图象的对称轴为x=?1;③2a+c=0;④a?b+c>0.其中正确的有(????)个.
A. 0 B. 1 C. 2 D. 3
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(?1,0)和B,与y轴交于点C.下列结论:①abc<0,②2a+b<0,③4a?2b+c>0,④3a+c>0,其中正确的结论个数为(????)
A. 1个
B. 2个
C. 3个
D. 4个
已知:抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(?1,0),其部分图象如图所示,下列结论:
①4ac
⑤当x<0时,y随x增大而增大
其中正确的结论有(????)
A. 4个 B. 3个 C. 2个 D. 1个
二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的部分图象如图所示,图象顶点的坐标为(2,1),与x轴的一个交点在点(3,0)和点(4,0)之间,有下列结论:①abc<0;②a?b+c>0;③c?4a=1;④b2>4ac;⑤am2+bm+c≤1(m为任意实数).其中正确的有(????)
A. 2个 B. 3个 C. 4个 D. 5个
二次函数y=ax2+bx+c的图象过点(?1,0),对称轴为直线x=2,若a>0,则下列结论错误的是(????)
A. 当x>2时,y随着x的增大而增大
B. (a+c)2=b2
C. 若A(x1,m)、B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c
D. 若方程a(x+1)(5?x)=?1的两根为x1、x2,且x1
A. 5 B. ?1 C. 5或1 D. ?5或?1
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
①ac>0;②a?b+c<0;③当x<0时,y<0;
④方程ax2+bx+c=0(a≠0)有两个大于?1的实数根.
其中错误的结论有(??? ).
A. ②③ B. ②④ C. ①③ D. ①④
二次函数y=ax2+bx+c的部分图象如图所示,对称轴是直线x=?1.5,与x轴的一个交点在(?4,0)和(?3,0)之间,有以下结论:①abc>0;②b2?4ac>0;③3a?b=0;④4b+3c<0.其中正确结论的个数是(????)
A. 1 B. 2 C. 3 D. 4
如图,抛物线y=?x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个判断:①当x>0时,y>0;②当x>1时,y随x的增大而减少;③m>?1;④当a=?1时,b=3;其中,判断正确的序号是(????)
A. ①② B. ②③ C. ①③ D. ②③④
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点(4,0),其对称轴为直线x=1,结合图象,下列结论:
①ac<0;
②4a?2b+c>0;
③当x>2时,y随x的增大而增大;
④关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根.
其中正确的结论有(????)
A. ①④
B. ③④
C. ①②④
D. ①③④
已知抛物线y=ax2+bx+c(a≠0)经过点(?1,0),(0,3),对称轴在y轴右侧,则下列结论:①a<0;②抛物线经过(1,0);③方程ax2+bx+c=1有两个不相等的实数根;④?3
如图,点A(2.18,?0.51),B(2.68,0.54),在二次函数y=ax2+bx+c(a≠0)的图象上,则方程ax2+bx+c=0的一个近似值可能是(????)
A. 2.18 B. 2.68 C. ?0.51 D. 2.45
答案和解析
1.【答案】C
【解析】
【分析】
本题考查了二次函数图象上点的坐标特征,抛物线与x轴的交点,属于中档题.
先计算自变量为0时对应的函数值得到抛物线与y轴的交点坐标;再把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程,解方程?x2+4x?4=0得抛物线与x轴的交点坐标,从而可对各选项进行判断.
【解答】
解:
当x=0时,y=?x2+4x?4=?4,则抛物线与y轴的交点坐标为(0,?4),
当y=0时,?x2+4x?4=0,解得x1=x2=2,抛物线与x轴的交点坐标为(2,0),
所以抛物线与坐标轴有2个交点.
故选C.??
2.【答案】D
【解析】
【分析】本题主要考查二次函数的对称轴和二次函数与一元二次方程的关系,难度不大.
根据对称轴方程?b2=2,得b=?4,解x2?4x=5即可.
【解答】
解由题意知函数图象的对称轴为直线x=2,
根据对称轴方程?b2=2,得b=?4,
代入方程得x2?4x?5=0,
解得x1=?1,x2=5,
故选D.
??
3.【答案】D
【解析】解:∵二次函数y=kx2?2x?l与x轴有交点,
∴△=(?2)2?4k×(?1)≥0,且k≠0,
解得k≥?1且k≠0,
故选:D.
根据二次函数的定义得到k≠0;根据一元二次方程kx2?2x?l=0的根的判别式的符号列出不等式,通过解不等式即可求得k的取值范围.
本题考查了抛物线与x轴的交点,二次函数的定义.注意二次函数解析式与一元二次方程间的关系.
4.【答案】A
【解析】解:A、由图象可知当x=1时,y>0,则a+b+c>0,故此选项正确;
B、由二次函数的图象开口向下可得a<0,故此选项错误;
C、由抛物线与x轴有两个交点可以看出方程ax2+bx+c=0的根的判别式b2?4ac>0,故此选项错误;
D、根据二次函数的图象与y轴交于负半轴知:c<0,故此选项错误;
故选:A.
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点得出c的值,然后根据抛物线与x轴交点的个数及x=1时二次函数的值的情况进行推理,进而对所得结论进行判断.
本题考查了图象与二次函数系数之间的关系,二次函数与方程之间的转换,根的判别式的熟练运用.会利用特殊值代入法求得特殊的式子,如:y=a+b+c,y=a?b+c,然后根据图象判断其值.
5.【答案】A
【解析】
【分析】
本题考查了抛物线与x轴的交点,二次函数图象上点的坐标特征,利用图象判断是解题的关键.
根据题意画出关于x的二次函数y=?x2?10x+m(m≠0)的图象以及直线y=?2,根据图象即可判断.
【解答】
解:由题意关于x的方程x2+10x?m?2=0有两个不相等的非零实数根x3,x4(x3
∵抛物线的对称轴为直线x=??102×(?1)=?5,
∴x3
6.【答案】C
【解析】解:A.∵抛物线开口向下,
∴a<0,
∵对称轴为直线x=?b2a=?1,
∴b=2a<0,
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc>0,
故A正确;
B.∵抛物线与x轴有两个交点,
∴b2?4ac>0,即4ac?b2<0,
故B正确;
C.∵抛物线的对称轴为直线x=?1,抛物线与x轴的一个交点在(?3,0)和(?2,0)之间,
∴抛物线与x轴的另一个交点在(0,0)和(1,0)之间,
∴x=1时,y<0,
即a+b+c<0,
∵b=2a,
∴3a+c<0,
故C错误;
D.∵抛物线开口向下,顶点为(?1,n),
∴函数有最大值n,
∴抛物线y=ax2+bx+c与直线y=n+1无交点,
∴一元二次方程ax2+bx+c=n+1无实数根,
故D正确.
故选:C.
根据抛物线开口方向,对称轴的位置以及与y轴的交点可以对A进行判断;根据抛物线与x轴的交点情况可对B进行判断;x=1时,y<0,可对C进行判断;根据抛物线y=ax2+bx+c与直线y=n+1无交点,可对D进行判断.
本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质.
7.【答案】D
【解析】解:①∵抛物线的对称轴为直线x=?b2a=?1,
∴b=2a,结论①错误;
②∵抛物线的对称轴为直线x=?1,抛物线与x轴一个交点的坐标为(1,0),
∴抛物线与x轴另一交点的坐标为(?3,0),
∴ax2+bx+c=0的两根分别为?3和1,结论②正确;
③∵抛物线开口向上,与y轴交于负半轴,
∴a>0,c<0,
∴a?2b+c=a?4a+c=?3a+c<0,结论③正确;
④∵当x=1时,y=0,
∴a+b+c=0,结论④正确;
⑤∵当x=2时,y>0,
∴4a+2b+c=8a+c>0,结论⑤正确.
综上所述:正确的结论有②③④⑤.
故选:D.
①由抛物线的对称轴为直线x=?1,可得出b=2a,结论①错误;②由抛物线的对称轴及抛物线与x轴一个交点的坐标,可求出另一交点坐标,进而可得出ax2+bx+c=0的两根分别为?3和1,结论②正确;③由抛物线的开口方向及抛物线与y轴交点的位置可得出a>0,c<0,结合b=2a,即可得出a?2b+c=?3a+c<0,结论③正确;④由当x=1时y=0,可得出a+b+c=0,结论④正确;⑤由当x=2时y>0结合b=2a,可得出4a+2b+c=8a+c>0,结论⑤正确.综上即可得出结论.
本题考查了二次函数图象与系数的关系、二次函数图象上点的坐标特征以及抛物线与x轴的交点,观察函数图象,逐一分析五个结论的正误是解题的关键.
8.【答案】C
【解析】解:对于①:二次函数开口向下,故a<0,与y轴的交点在y的正半轴,故c>0,故ac<0,因此①错误;
对于②:二次函数的图象与x轴相交于A(?2,0)、B(1,0),由对称性可知,其对称轴为:x=?2+12=?12,因此②错误;
对于③:设二次函数y=ax2+bx+c的交点式为y=a(x+2)(x?1)=ax2+ax?2a,比较一般式与交点式的系数可知:b=a,c=?2a,故2a+c=0,因此③正确;
对于④:当x=?1时对应的y=a?b+c,观察图象可知x=?1时对应的函数图象的y值在x轴上方,故a?b+c>0,因此④正确.
∴只有③④是正确的.
故选:C.
根据抛物线的开口方向、对称轴、顶点坐标、增减性以及过特殊点时系数a、b、c满足的关系综合判断即可.
本题考查了二次函数的图象与其系数的关系及二次函数的对称性,熟练掌握二次函数的图象性质是解决此类题的关键.
9.【答案】B
【解析】解:①∵由抛物线的开口向上知a>0,
∵对称轴位于y轴的右侧,
∴b<0.
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc>0;
故错误;
②对称轴为x=?b2a<1,得2a>?b,即2a+b>0,
故错误;
③如图,当x=?2时,y>0,4a?2b+c>0,
故正确;
④∵当x=?1时,y=0,
∴0=a?b+c
故正确.
综上所述,有2个结论正确.
故选:B.
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴求出2a与b的关系.
本题主要考查抛物线与x轴的交点坐标,二次函数图象与函数系数之间的关系,解题的关键是掌握数形结合思想的应用,注意掌握二次函数图象与系数的关系.
10.【答案】B
【解析】解:①∵抛物线与x轴有2个交点,
∴b2?4ac>0,即4ac
而点(?1,0)关于直线x=1的对称点的坐标为(3,0),
∴方程ax2+bx+c=0的两个根是x1=?1,x2=3,所以②正确;
③∵抛物线y=ax2+bx+c(a≠0)经过点(?1,0),
∴a?b+c=0,所以③错误;
④∵抛物线与x轴的两点坐标为(?1,0),(3,0),
∴当?1
⑤∵抛物线的对称轴为直线x=1,
∴当x<1时,y随x增大而增大,所以⑤正确.
故选B.
利用抛物线与x轴的交点个数可对①进行判断;利用抛物线的对称性得到抛物线与x轴的一个交点坐标为(3,0),则可对②进行判断;根据抛物线过点(?1,0),则可对③进行判断;根据抛物线在x轴上方所对应的自变量的范围可对④进行判断;根据二次函数的性质对⑤进行判断.
本题考查了二次函数图象与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点位置:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2?4ac>0时,抛物线与x轴有2个交点;△=b2?4ac=0时,抛物线与x轴有1个交点;△=b2?4ac<0时,抛物线与x轴没有交点.
11.【答案】B
【解析】解:由图象可知,抛物线开口向下,对称轴在y轴的右侧,与y轴的交点在y轴的负半轴,
∴a<0,b>0,c<0,
∴abc>0,故①错误;
由图象可知,x=?1时,y<0,
∴a?b+c<0,故②错误;
∵抛物线的顶点坐标为(2,1),
∴?b2a=2,b=?4a,
∵4a+2b+c=1,
∴4a?8a+c=1,即c?4a=1,故③正确;
∵抛物线与x轴有两个交点,
∴△>0,
∴b2?4ac>0,即b2>4ac,故④正确.
∵抛物线的开口向下,顶点坐标为(2,1),
∴am2+bm+c≤1(m为任意实数),故⑤正确.
故选:B.
①抛物线的开口方向,对称轴以及与y轴的交点即可判断;
②根据x=?1时,y<0,即可判断.
③根据对称轴x=?b2a=2,即可判断.
③根据抛物线与x轴有两个交点,可知△>0,即可判断.
④根据抛物线的顶点坐标为(2,1),函数有最大值,由此即可判断.
本题考查二次函数与x轴的交点、二次函数的图象与系数的关系等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
12.【答案】D
【解析】解:∵二次函数y=ax2+bx+c中,a>0,对称轴为直线x=2,
∴当x>2时,y随着x的增大而增大,故A正确;
∵?b2a=2,
∴b=?4a,
∵二次函数y=ax2+bx+c的图象过点(?1,0),
∴a?b+c=0,即a+4a+c=0,
∴c=?5a,
∴a+c=?4a,
∴(a+c)2=b2,故B正确;
∵A(x1,m)、B(x2,m)是抛物线上的两点,
∴抛物线对称轴x=x1+x22,
∴2x=x1+x2,
∵x=x1+x2,
∴2x=x,
∴x=0,
∴此时,y=ax2+bx+c=c,故C正确;
∵抛物线的对称轴为直线x=2,图象与x轴交于(?1,0),
∴抛物线x轴的另一个交点是(5,0),
∴抛物线与直线y=?1的交点横坐标x1>?1,x2<5,如图,
∴方程a(x+1)(x?5)=?1的两根为x1和x2,且x1
根据二次函数的性质即可判断A;根据对称轴得到b=?4a,经过点(?1,0)得到c=?5a,从而求得a+c=?4a,即可判断B;由抛物线的对称性得到x=x1+x22,结合x=x1+x2,即可判断C;利用二次函数与一元二次方程的关系即可判断D.
本题考查了二次函数图象与系数的关系,二次函数图象上点的坐标特征,二次函数的性质,抛物线与x轴的交点,熟练掌握二次函数的性质是解题的关键.
13.【答案】B
【解析】解:∵对称轴为直线x=2,
∴b=?4,
∴y=x2?4x,
关于x的一元二次方程x2+bx?t=0的解可以看成二次函数y=x2?4x与直线y=t的交点,
∵?1
∴?4≤t<5;
故选:B.
先求出b,确定二次函数解析式,关于x的一元二次方程x2+bx?t=0的解可以看成二次函数y=x2?4x与直线y=t的交点,?1
14.【答案】C
【解析】解:∵抛物线y=a(x??)2+k的对称轴为直线x=?,抛物线y=a(x???m)2+k的对称轴为直线x=?+m,
∴当点A(?1,0)平移后的对应点为(4,0),则m=4?(?1)=5;
当点B(3,0)平移后的对应点为(4,0),则m=4?3=1,
即m的值为5或1.
故选:C.
先利用二次函数的性质得到两抛物线的对称轴,然后利用A点或B点向右平移得到点(4,0)得到m的值.
本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质.
15.【答案】C
【解析】
【分析】
此题主要考查了二次函数图像与系数的关系,二次函数性质等内容,解题关键是利用图象求出a,b,c的范围,以及特殊值的代入能得到特殊的式子,如:当x=1时,y>0,a+b+c>0;x=?1时,y<0,a?b+c<0.
①由二次函数y=ax2+bx+c(a≠0)的图象开口方向知道a<0,与y轴交点知道c>0,由此即可确定ac的符号;
②由于当x=?1时,y=a?b+c,而根据图象知道当x=?1时y<0,由此即可判定a?b+c的符号;
③根据图象知道当x<0时,y
【解答】
解:∵图象开口向下,∴a<0,
∵图象与y轴交于正半轴,则c>0,
∴ac<0,故选项①错误;
∵当x=?1时,对应y值小于0,即a?b+c<0,故选项②正确;
当x<0时,y
故选;C.??
16.【答案】D
【解析】解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线x=?b2a=?1.5,
∴b=3a<0,
∴3a?b=0,所以③正确;
∵抛物线交y的正半轴,
∴c>0,
∴abc>0,所以①正确;
∵抛物线与x轴有两个交点,
∴b2?4ac>0,所以②正确;
由图象可知,x=1时y<0,且b=3a,
即a+b+c=13b+b+c=43b+c<0,
即4b+3c<0,故④正确;
故选:D.
根据抛物线开口方向,对称轴以及与y轴的交点即可判断①③;根据抛物线与x轴的交点即可判断②;由图象可知,x=1时y<0,且b=3a,即可得到a+b+c=13b+b+c=43b+c<0,即可判断④.
本题考查了二次函数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab<0),对称轴在y轴右.常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由Δ决定:Δ=b2?4ac>0时,抛物线与x轴有2个交点;Δ=b2?4ac=0时,抛物线与x轴有1个交点;Δ=b2?4ac<0时,抛物线与x轴没有交点.
17.【答案】D
【解析】解:①由图象可知,当x>0时,y可以小于0,故①错误;
②∵抛物线的对称轴为x=?22×(?1)=1,
∴当x>1时,y随x的增大而减少,故②正确;
③由图象可知m+1>0,
∴m>?1,故③正确;
④若a=?1,则A(?1,0),抛物线的对称轴为x=1,
∴B(3,0),
∴b=3,故④正确;
故选:D.
根据函数图象即可判断①;求得对称轴为直线x=1,观察图象即可判断②;由抛物线与y轴的交点即可判断③;根据抛物线的对称性即可判断④.
本题考查了二次函数图象与系数的关系,二次函数的性质,数形结合是解题的关键.
18.【答案】D
【解析】解:抛物线开口向上,因此a>0,与y轴交于负半轴,因此c<0,故ac<0,所以①正确;
抛物线对称轴为x=1,与x轴的一个交点为(4,0),则另一个交点为(?2,0),于是有4a?2b+c=0,所以②不正确;
x>1时,y随x的增大而增大,所以③正确;
抛物线与x轴有两个不同交点,因此关于x的一元二次方程ax2+bx+c=0有两个不相等的实数根,所以④正确;
综上所述,正确的结论有:①③④,
故选:D.
根据抛物线的开口方向、对称轴、顶点坐标、增减性以及与x轴y轴的交点,综合判断即可.
本题考查二次函数的图象和性质,掌握二次函数的图象与系数之间的关系是正确判断的前提.
19.【答案】C
【解析】解:①∵抛物线y=ax2+bx+c(a≠0)经过点(?1,0),(0,3),对称轴在y轴右侧,
∴抛物线开口向下,
∴a<0,结论①正确;
②∵抛物线过点(?1,0),对称轴在y轴右侧,
∴当x=1时y>0,结论②错误;
③∵顶点的纵坐标大于3,
∴过点(0,1)作x轴的平行线与抛物线有两个交点,
∴方程ax2+bx+c=1有两个不相等的实数根,结论③正确;
④∵当x=1时y=a+b+c>0,
∴a+b>?c.
∵抛物线y=ax2+bx+c(a,b,c为常数,a≠0)经过点(0,3),
∴c=3,
∴a+b>?3.
∵当x=?1时,y=0,即a?b+c=0,
∴b=a+c,
∴a+b=2a+c.
∵抛物线开口向下,
∴a<0,
∴a+b
①由抛物线y=ax2+bx+c(a≠0)经过点(?1,0),(0,3),对称轴在y轴右侧,即可判断开口向下,结论①正确;
②由抛物线过点(?1,0),对称轴在y轴右侧,即可得出当x=1时y>0,结论①错误;
②过点(0,1)作x轴的平行线,由该直线与抛物线有两个交点,可得出方程ax2+bx+c=1有两个不相等的实数根,结论③正确;
④由当x=1时y>0,可得出a+b>?c,由抛物线与y轴交于点(0,3)可得出c=3,进而即可得出a+b>?3,由抛物线过点(?1,0)可得出a+b=2a+c,结合a<0、c=3可得出a+b<3,综上可得出?3
20.【答案】D
【解析】解:∵图象上有两点分别为A(2.18,?0.51)、B(2.68,0.54),
∴当x=2.18时,y=?0.51;x=2.68时,y=0.54,
∴当y=0时,2.18
故选:D.
根据自变量两个取值所对应的函数值是?0.51和0.54,可得当函数值为0时,x的取值应在所给的自变量两个值之间.
本题考查了图象法求一元二次方程的近似值,用到的知识点为:点在函数解析式上,点的横纵坐标适合这个函数解析式;二次函数值为0,就是函数图象与x轴的交点,跟所给的接近的函数值对应的自变量相关.
同课章节目录
