3.3 勾股定理的应用举例 课件(共21张PPT)
文档属性
| 名称 | 3.3 勾股定理的应用举例 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 00:00:00 | ||
图片预览







文档简介
第三章 勾股定理
3 勾股定理的应用举例
知识点一 确定几何体上的最短路线
在平面上寻找两点之间最短路线的依据是线段公理:两点之间,线段最短在立体图形上,由于受物体和空间的阻隔,两点间的最短路线不一定是连接两点的线段,应将立体图形展开成平面图形,然后确定最短路线步骤如下.
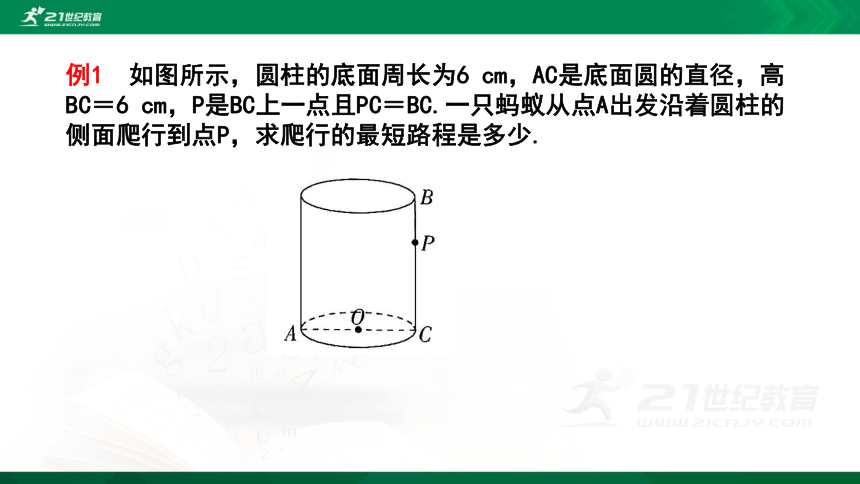
例1 如图所示,圆柱的底面周长为6 cm,AC是底面圆的直径,高BC=6 cm,P是BC上一点且PC=BC.一只蚂蚁从点A出发沿着圆柱的侧面爬行到点P,求爬行的最短路程是多少.
知识点二 利用直角三角形的判别条件
在实际生活中,常判断两直线是否垂直,解决此类问题的一般方法是将实际问题转化为数学问题,先结合题意画出符合要求的三角形,再利用直角三角形的判别条件判断是否垂直.
例2 下图是一农民建房时挖地基的平面图,按标准,四边形ABCD应为长方形,他在挖完后测得AB=CD=6 m,AD=BC=8 m,AC=9 m,请你帮他检查一下挖的地基是否合格.
例2 下图是一农民建房时挖地基的平面图,按标准,四边形ABCD应为长方形,他在挖完后测得AB=CD=6 m,AD=BC=8 m,AC=9 m,请你帮他检查一下挖的地基是否合格.
解析: AD2+DC2=82+62=100,AC2=92=81,
∴AD2+DC2≠AC2,∴△ADC不是直角三角形,∴∠ADC≠90°.
∵四边形ABCD应为长方形,∴四个角应为直角,
∴该农民挖的地基不合格.
知识点三 应用勾股定理
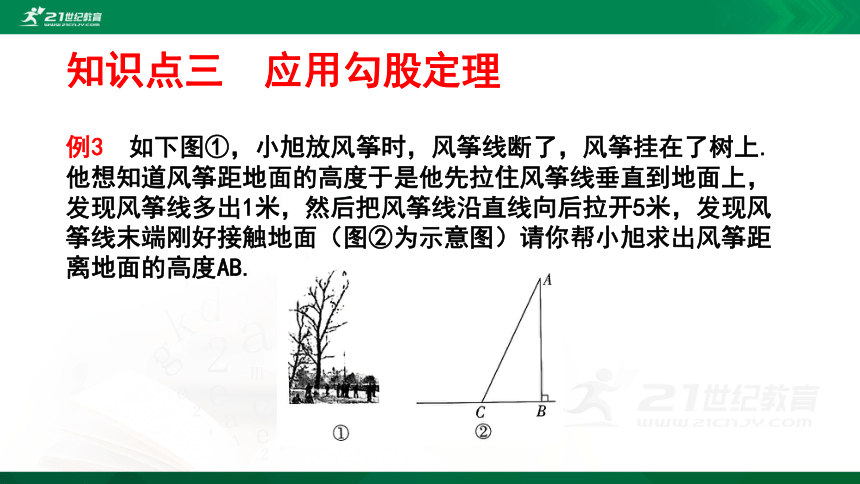
例3 如下图①,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度于是他先拉住风筝线垂直到地面上,发现风筝线多出1米,然后把风筝线沿直线向后拉开5米,发现风筝线末端刚好接触地面(图②为示意图)请你帮小旭求出风筝距离地面的高度AB.
解析 设AB=x,则AC=x+1,
由题意可得∠ABC=90°,BC=5,
在Rt△ABC中,AB2+BC2=AC2,即x2+52=(x+1)2,解得x=12.
答:风筝距离地面的高度AB为12米.
解析 设AB=x,则AC=x+1,
由题意可得∠ABC=90°,BC=5,
在Rt△ABC中,AB2+BC2=AC2,即x2+52=(x+1)2,解得x=12.
答:风筝距离地面的高度AB为12米.
点拨 在应用勾股定理解决实际问题时,勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出直角三角形这一数学模型,画出准确的示意图.
经典例题
题型 勾股定理在折叠问题中的应用
例题 下图①是一个直角三角形纸片,∠C=90°,AB=13cm,BC=5cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD(如图②),求DC的长.
易错易混
易错点 将长方体展开时,考虑不全
对长方体来说,一般情况下,展开的方法不同,展开得到的两点间的距离也不相同,故对此问题应把可能出现的情况考虑全,分别计算,经过比较求出最短距离.
例题 如图所示,长方体ABCD-A′B′C′D′中,AB=BB′=2,AD=3,一只蚂蚁从A点出发,沿长方体表面爬到C′点,最短路程是多少?
(2)如下图,将长方体的前面和上面展开至同一平面,得长方形ADC′B′,AD=3,C′D=DD′+D′C′=2+2=4,连接AC′,则△ADC′为直角三角形,由勾股定理得AC′2=C′D2+AD2=42+32=25. ∴AC′=5.
易错分析
本题易出现只考虑其中一种情况,而忽视其他情况的错误.
3 勾股定理的应用举例
知识点一 确定几何体上的最短路线
在平面上寻找两点之间最短路线的依据是线段公理:两点之间,线段最短在立体图形上,由于受物体和空间的阻隔,两点间的最短路线不一定是连接两点的线段,应将立体图形展开成平面图形,然后确定最短路线步骤如下.
例1 如图所示,圆柱的底面周长为6 cm,AC是底面圆的直径,高BC=6 cm,P是BC上一点且PC=BC.一只蚂蚁从点A出发沿着圆柱的侧面爬行到点P,求爬行的最短路程是多少.
知识点二 利用直角三角形的判别条件
在实际生活中,常判断两直线是否垂直,解决此类问题的一般方法是将实际问题转化为数学问题,先结合题意画出符合要求的三角形,再利用直角三角形的判别条件判断是否垂直.
例2 下图是一农民建房时挖地基的平面图,按标准,四边形ABCD应为长方形,他在挖完后测得AB=CD=6 m,AD=BC=8 m,AC=9 m,请你帮他检查一下挖的地基是否合格.
例2 下图是一农民建房时挖地基的平面图,按标准,四边形ABCD应为长方形,他在挖完后测得AB=CD=6 m,AD=BC=8 m,AC=9 m,请你帮他检查一下挖的地基是否合格.
解析: AD2+DC2=82+62=100,AC2=92=81,
∴AD2+DC2≠AC2,∴△ADC不是直角三角形,∴∠ADC≠90°.
∵四边形ABCD应为长方形,∴四个角应为直角,
∴该农民挖的地基不合格.
知识点三 应用勾股定理
例3 如下图①,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度于是他先拉住风筝线垂直到地面上,发现风筝线多出1米,然后把风筝线沿直线向后拉开5米,发现风筝线末端刚好接触地面(图②为示意图)请你帮小旭求出风筝距离地面的高度AB.
解析 设AB=x,则AC=x+1,
由题意可得∠ABC=90°,BC=5,
在Rt△ABC中,AB2+BC2=AC2,即x2+52=(x+1)2,解得x=12.
答:风筝距离地面的高度AB为12米.
解析 设AB=x,则AC=x+1,
由题意可得∠ABC=90°,BC=5,
在Rt△ABC中,AB2+BC2=AC2,即x2+52=(x+1)2,解得x=12.
答:风筝距离地面的高度AB为12米.
点拨 在应用勾股定理解决实际问题时,勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出直角三角形这一数学模型,画出准确的示意图.
经典例题
题型 勾股定理在折叠问题中的应用
例题 下图①是一个直角三角形纸片,∠C=90°,AB=13cm,BC=5cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD(如图②),求DC的长.
易错易混
易错点 将长方体展开时,考虑不全
对长方体来说,一般情况下,展开的方法不同,展开得到的两点间的距离也不相同,故对此问题应把可能出现的情况考虑全,分别计算,经过比较求出最短距离.
例题 如图所示,长方体ABCD-A′B′C′D′中,AB=BB′=2,AD=3,一只蚂蚁从A点出发,沿长方体表面爬到C′点,最短路程是多少?
(2)如下图,将长方体的前面和上面展开至同一平面,得长方形ADC′B′,AD=3,C′D=DD′+D′C′=2+2=4,连接AC′,则△ADC′为直角三角形,由勾股定理得AC′2=C′D2+AD2=42+32=25. ∴AC′=5.
易错分析
本题易出现只考虑其中一种情况,而忽视其他情况的错误.
