7.3.1 圆的标准方程课件-湘教版必修3(19张PPT)
文档属性
| 名称 | 7.3.1 圆的标准方程课件-湘教版必修3(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 412.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 00:00:00 | ||
图片预览





文档简介
7.3.1 圆的标准方程
4.1.1 圆的标准方程
我们在前面学过,在平面直角坐标系中,两点确定一条直线,一点和倾斜角也能确定一条直线.在平面直角坐标系中,如何确定一个圆呢?
复习引入
问题1
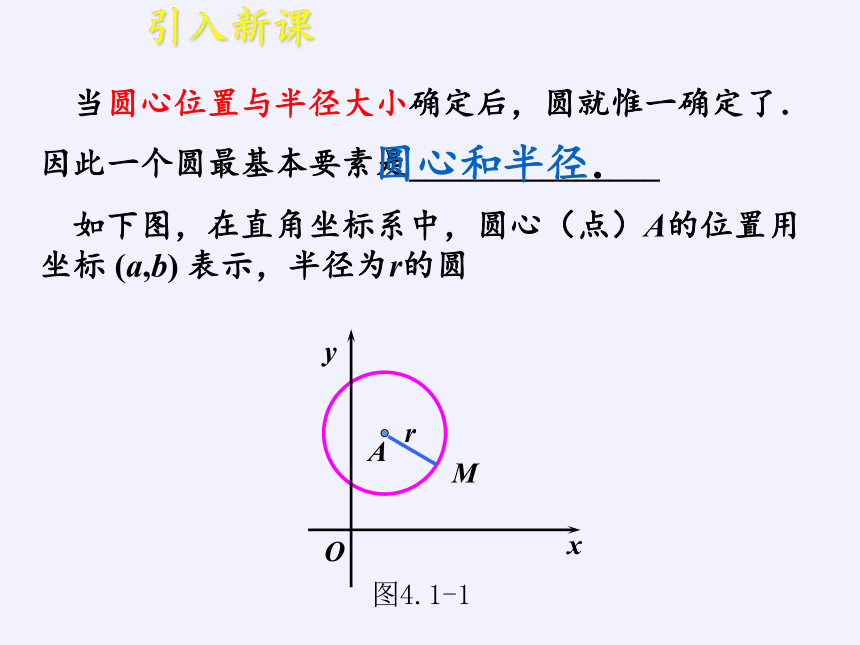
当圆心位置与半径大小确定后,圆就惟一确定了.
因此一个圆最基本要素是_______________
引入新课
如下图,在直角坐标系中,圆心(点)A的位置用坐标 (a,b) 表示,半径为r的圆
x
O
y
A
M
r
图4.1-1
圆心和半径.
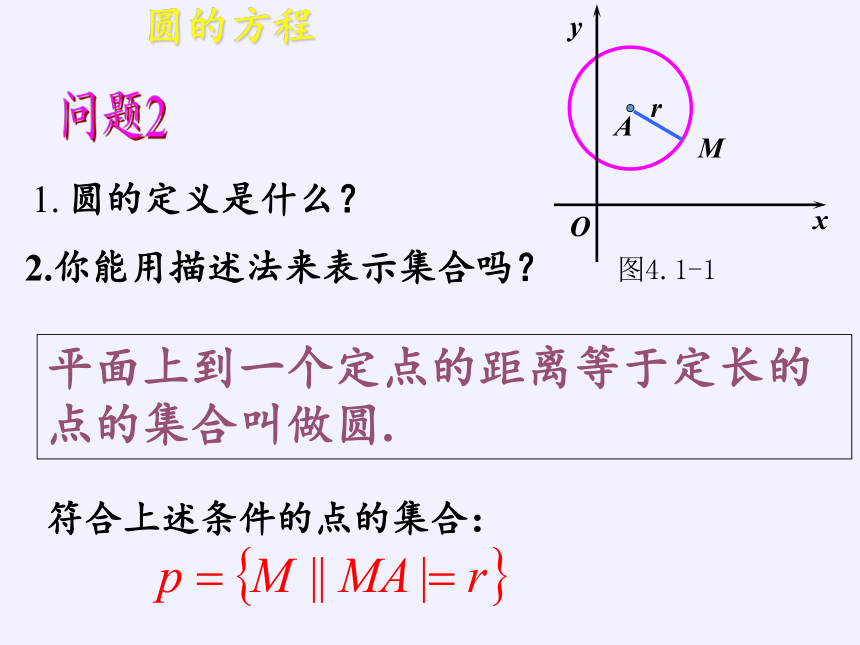
1. 圆的定义是什么?
2.你能用描述法来表示集合吗?
符合上述条件的点的集合:
圆的方程
问题2
x
O
y
A
M
r
图4.1-1
平面上到一个定点的距离等于定长的点的集合叫做圆.
圆的方程
1.两点间距离公式如何表示?
则点M、A间的距离为:
由:
2.圆上任意点M(x, y)与圆心A (a,b)之间的距离怎样表示?
问题3
圆的标准方程
点M(x, y)在圆上,由前面讨论可知,点M的坐标适合方程;反之,若点M(x, y)的坐标适合方程,这就说明点 M与圆心的距离是 r ,即点M在圆心为A (a, b),半径为r的圆上.
把这个方程称为圆心为A(a, b),半径长为r 的圆的方程,把它叫做圆的标准方程.
明确:三个条件a、b、r确定一个圆
特殊位置的圆方程
因为圆心是原点O(0, 0),将a=0,b=0和半径 r 带入圆的标准方程:
问题4
圆心在坐标原点,半径长为r 的圆的方程是什么?
得:
整理得:
1 (口答) 、求圆的圆心及半径
(1)、x2+y2=4 (2)、(x+1)2+y2=1
热身练习
X
y
0
+2
-2
C(0、0) r=2
X
Y
0
-1
C(-1、0) r=1
(1) x2+y2=9
(2) (x+3)2+(y-4)2=5
热身练习
2、写出下列圆的方程
(1)、圆心在原点,半径为3;
(2)、圆心在(-3、4),半径为 .
例1 写出圆心为 ,半径长等于5的圆的方程,并判断点 , 是否在这个圆上.
解:圆心是 ,半径长等于5的圆的标准
方程是:
典型例题(点和圆的位置关系)
把 的坐标代入方程 左右两边相等,点 的坐标适合圆的方程,所以点 在这个圆上;
把点 的坐标代入此方程,左右两边不相等,点 的坐标不适合圆的方程,所以点 不在这个圆上.
从上题知道,判断一个点在不在某个圆上,只需将这个点的坐标带入这个圆的方程,如果能使圆的方程成立,则在这个圆上,反之如果不成立则不在这个圆上.
例2 的三个顶点的坐标分别A(5,1),
B(7,-3),C(2, -8),求它的外接圆的方程.
分析:不在同一条直线上的三个点可以确定一个圆,三角形有唯一的外接圆.
解:设所求圆的方程是 (1)
因为A(5,1), B(7,-3),C(2, -8) 都在圆上,所以它们的坐标都满足方程(1).
典型例题(求圆的方程)
所以, 的外接圆的方程为 .
典型例题
解此方程组,得:
于是有
有无其他方法?
待定系数法
数形结合法
训练 已知圆心为C 的圆经过点A(1, 1)和B(2, -2),且圆心C 在直线上l:x-y+1=0,求圆心为C 的圆的标准方程.
x
y
O
l
●
B
A
C
l’
图4.1-3
典型例题(求圆的方程)
因此线段AB的垂直平分线 的方程是
即
圆心C 的坐标是方程组
的解,
典型例题
直线AB 的斜率:
解:因为A(1, 1)和B(2, -2),所以线段AB 的中点D 的
坐标为
所以圆心C 的坐标是
圆心为C 的圆的半径长
所以,圆心为C 的圆的标准方程是:
典型例题
解此方程组,得
数形结合法
牢记:1. 圆的标准方程:(x-a)2+(y-b)2=r2;
2.圆心在原点:x2+y2=r2;
明确:三个条件a、b、r确定一个圆;
方法:①代数法(待定系数法)
②几何法(数形结合法)
知识小结
结束
谢 谢
4.1.1 圆的标准方程
我们在前面学过,在平面直角坐标系中,两点确定一条直线,一点和倾斜角也能确定一条直线.在平面直角坐标系中,如何确定一个圆呢?
复习引入
问题1
当圆心位置与半径大小确定后,圆就惟一确定了.
因此一个圆最基本要素是_______________
引入新课
如下图,在直角坐标系中,圆心(点)A的位置用坐标 (a,b) 表示,半径为r的圆
x
O
y
A
M
r
图4.1-1
圆心和半径.
1. 圆的定义是什么?
2.你能用描述法来表示集合吗?
符合上述条件的点的集合:
圆的方程
问题2
x
O
y
A
M
r
图4.1-1
平面上到一个定点的距离等于定长的点的集合叫做圆.
圆的方程
1.两点间距离公式如何表示?
则点M、A间的距离为:
由:
2.圆上任意点M(x, y)与圆心A (a,b)之间的距离怎样表示?
问题3
圆的标准方程
点M(x, y)在圆上,由前面讨论可知,点M的坐标适合方程;反之,若点M(x, y)的坐标适合方程,这就说明点 M与圆心的距离是 r ,即点M在圆心为A (a, b),半径为r的圆上.
把这个方程称为圆心为A(a, b),半径长为r 的圆的方程,把它叫做圆的标准方程.
明确:三个条件a、b、r确定一个圆
特殊位置的圆方程
因为圆心是原点O(0, 0),将a=0,b=0和半径 r 带入圆的标准方程:
问题4
圆心在坐标原点,半径长为r 的圆的方程是什么?
得:
整理得:
1 (口答) 、求圆的圆心及半径
(1)、x2+y2=4 (2)、(x+1)2+y2=1
热身练习
X
y
0
+2
-2
C(0、0) r=2
X
Y
0
-1
C(-1、0) r=1
(1) x2+y2=9
(2) (x+3)2+(y-4)2=5
热身练习
2、写出下列圆的方程
(1)、圆心在原点,半径为3;
(2)、圆心在(-3、4),半径为 .
例1 写出圆心为 ,半径长等于5的圆的方程,并判断点 , 是否在这个圆上.
解:圆心是 ,半径长等于5的圆的标准
方程是:
典型例题(点和圆的位置关系)
把 的坐标代入方程 左右两边相等,点 的坐标适合圆的方程,所以点 在这个圆上;
把点 的坐标代入此方程,左右两边不相等,点 的坐标不适合圆的方程,所以点 不在这个圆上.
从上题知道,判断一个点在不在某个圆上,只需将这个点的坐标带入这个圆的方程,如果能使圆的方程成立,则在这个圆上,反之如果不成立则不在这个圆上.
例2 的三个顶点的坐标分别A(5,1),
B(7,-3),C(2, -8),求它的外接圆的方程.
分析:不在同一条直线上的三个点可以确定一个圆,三角形有唯一的外接圆.
解:设所求圆的方程是 (1)
因为A(5,1), B(7,-3),C(2, -8) 都在圆上,所以它们的坐标都满足方程(1).
典型例题(求圆的方程)
所以, 的外接圆的方程为 .
典型例题
解此方程组,得:
于是有
有无其他方法?
待定系数法
数形结合法
训练 已知圆心为C 的圆经过点A(1, 1)和B(2, -2),且圆心C 在直线上l:x-y+1=0,求圆心为C 的圆的标准方程.
x
y
O
l
●
B
A
C
l’
图4.1-3
典型例题(求圆的方程)
因此线段AB的垂直平分线 的方程是
即
圆心C 的坐标是方程组
的解,
典型例题
直线AB 的斜率:
解:因为A(1, 1)和B(2, -2),所以线段AB 的中点D 的
坐标为
所以圆心C 的坐标是
圆心为C 的圆的半径长
所以,圆心为C 的圆的标准方程是:
典型例题
解此方程组,得
数形结合法
牢记:1. 圆的标准方程:(x-a)2+(y-b)2=r2;
2.圆心在原点:x2+y2=r2;
明确:三个条件a、b、r确定一个圆;
方法:①代数法(待定系数法)
②几何法(数形结合法)
知识小结
结束
谢 谢
