7.3.1 圆的标准方程(1)课件-湘教版必修3(27张PPT)
文档属性
| 名称 | 7.3.1 圆的标准方程(1)课件-湘教版必修3(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 523.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 00:00:00 | ||
图片预览








文档简介
7.3.1 圆的标准方程
1.会用定义推导圆的标准方程;掌握圆的标准方程的特点.
2.会根据已知条件求圆的标准方程.
3.能准确判断点与圆的位置关系.
重点:圆的标准方程理解及运用
难点:根据不同条件,利用待定系数求圆的标准方程。
一、学习目标:
二、重点、难点:
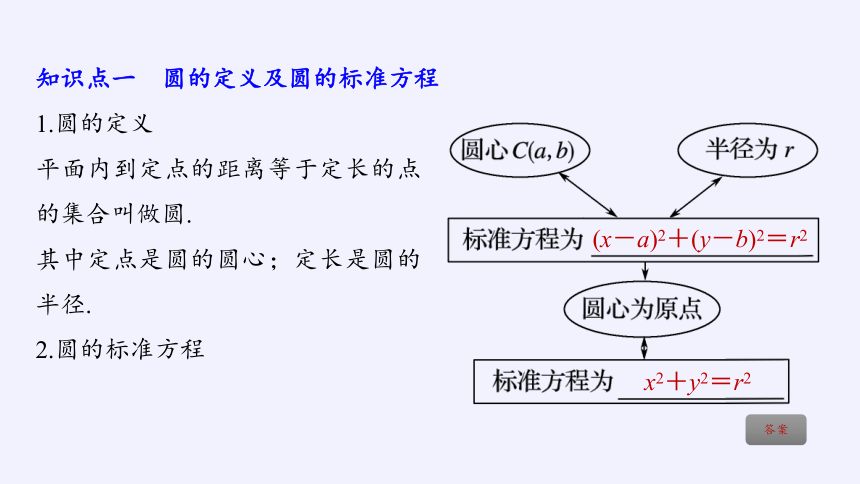
知识点一 圆的定义及圆的标准方程
1.圆的定义
答案
(x-a)2+(y-b)2=r2
x2+y2=r2
平面内到定点的距离等于定长的点的集合叫做圆.
其中定点是圆的圆心;定长是圆的半径.
2.圆的标准方程
知识点二 点与圆的位置关系
点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2的位置关系及判断方法
位置关系
利用距离判断
利用方程判断
点M在圆上
点M在圆外
点M在圆内
B
C
3.圆心在直线x=2上的圆C与y轴交于两点A(0,-4),B(0,-2),则圆C的方程为__________________.
(x-2)2+(y+3)2=5
探究一:
在平面直角坐标系中,如何确定一个圆呢?
在直角坐标系中,圆心A(a,b) ,半径r等于圆上任意点M(x, y)与圆心A (a,b) 的距离.
符合上述条件的点M(x, y)集合是什么?你能用描述法来表示这个集合吗?
x
O
y
M
r
(x, y)
A
(a,b)
探究二:
圆上任意点M(x, y)与圆心A (a,b)之间的距离能用什么公式表示?
根据两点间距离公式:
则点M、A间的距离为:
即:
问:方程 一定表示圆吗?
方程有什么特点呢?
圆心在坐标原点,半径长为r 的圆的方程是什么?
因为圆心是原点O(0, 0),将x=0,y=0和半径 r 带入圆的标准方程:
得:
整理得:
探究三:
怎样判断点 在圆 内呢?还是在圆外呢?
可以看到:点在圆外——点到圆心的距离大于半径 r ;
点在圆内——点到圆心的距离小于半径 r .
x
y
o
M2
M1
M3
A
探究三:
点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2的位置关系
位置关系
利用距离判断
利用方程判断
点M在圆上
|CM|=r
(x0-a)2+(y0-b)2=r2
点M在圆外
|CM|>r
(x0-a)2+(y0-b)2>r2
点M在圆内
|CM|(x0-a)2+(y0-b)2 例1 写出圆心为 ,半径长等于5的圆的方程,并判断点 , 是否在这个圆上。
解:圆心是 ,半径长等于5的圆的标准方程是:
把 的坐标代入方程 左右两边相等,点 的坐标适合圆的方程,所以点
在这个圆上;
把点 的坐标代入此方程,左右两边不相等,点 的坐标不适合圆的方程,所以点 不在这个圆上.
待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
例2 ⊿ABC的三个顶点的坐标分别是A(5,1),
B(7,-3),C(2,-8),求它的外接圆的方程。
例3 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.
B
x
o
y
A
C
l
解:∵A(1,1),B(2,-2)
例3 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.
即:x-3y-3=0
∴圆心C(-3,-2)
方法2 设所求圆的标准方程为(x-a)2+(y-b)2=r2,
方法3 因为圆心在直线x-y+1=0上,
所以可设圆心C的坐标为(a,a+1).又因为|CA|=|CB|,
解得a=-3.
当堂检测
1
2
3
4
5
解析答案
C
解析答案
2.圆心是O(-3,4),半径长为5的圆的方程为( )
A.(x-3)2+(y+4)2=5
B.(x-3)2+(y+4)2=25
C.(x+3)2+(y-4)2=5
D.(x+3)2+(y-4)2=25
D
解析 将O(-3,4),r=5代入圆的标准方程可得.
1
2
3
4
5
1
2
3
4
5
解析答案
3.经过点(2,2),圆心为C(1,1)的圆的方程是( )
A.(x+1)2+(y+1)2=2
B.(x-1)2+(y-1)2=2
C.(x+1)2+(y+1)2=2
D.(x-1)2+(y-1)2=2
?
B
故圆的标准方程为(x-1)2+(y-1)2=2.
解析答案
4.点P(5a+1,12a)在圆(x-1)2+y2=1的外部,则a的取值范围为( )
D
1
2
3
4
5
1
2
3
4
5
解析答案
解析 由题意知圆C的圆心为(0,1),半径为1,
所以圆C的标准方程为x2+(y-1)2=1.
5.若圆C的半径为1,其圆心与点(1,0)关于直线y=x对称,则圆C的标准方程为_______________.
x2+(y-1)2=1
题型探究 重点突破
6.已知圆过两点A(3,1),B(-1,3),且它的圆心在直线3x-y-2=0上,求此圆的标准方程.
解析答案
反思与感悟
解 方法一 设所求圆的标准方程为(x-a)2+(y-b)2=r2,
解析答案
反思与感悟
故所求圆的标准方程为(x-2)2+(y-4)2=10.
所以线段AB的垂直平分线m的斜率为2.
解析答案
反思与感悟
因此直线m的方程为y-2=2(x-1),
即2x-y=0.
又因为圆心在直线3x-y-2=0上,
所以圆心是这两条直线的交点.
设圆心为C,所以圆心坐标为(2,4).
反思与感悟
所以所求圆的标准方程为(x-2)2+(y-4)2=10.
方法三 设圆心为C.
因为圆心在直线3x-y-2=0上,
所以可设圆心C的坐标为(a,3a-2).
又因为|CA|=|CB|,
解得a=2.
故所求圆的标准方程为(x-2)2+(y-4)2=10.
课堂小结
1.确定圆的方程主要方法是待定系数法,即列出关于a,b,r的方程组求a,b,r或直接求出圆心(a,b)和半径r.另外依据题意适时运用圆的几何性质解题可以化繁为简,提高解题效率.
2.讨论点与圆的位置关系可以从代数特征(点的坐标是否满足圆的方程)或几何特征(点到圆心的距离与半径的关系)去考虑,其中利用几何特征较为直观、快捷.
返回
谢 谢
1.会用定义推导圆的标准方程;掌握圆的标准方程的特点.
2.会根据已知条件求圆的标准方程.
3.能准确判断点与圆的位置关系.
重点:圆的标准方程理解及运用
难点:根据不同条件,利用待定系数求圆的标准方程。
一、学习目标:
二、重点、难点:
知识点一 圆的定义及圆的标准方程
1.圆的定义
答案
(x-a)2+(y-b)2=r2
x2+y2=r2
平面内到定点的距离等于定长的点的集合叫做圆.
其中定点是圆的圆心;定长是圆的半径.
2.圆的标准方程
知识点二 点与圆的位置关系
点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2的位置关系及判断方法
位置关系
利用距离判断
利用方程判断
点M在圆上
点M在圆外
点M在圆内
B
C
3.圆心在直线x=2上的圆C与y轴交于两点A(0,-4),B(0,-2),则圆C的方程为__________________.
(x-2)2+(y+3)2=5
探究一:
在平面直角坐标系中,如何确定一个圆呢?
在直角坐标系中,圆心A(a,b) ,半径r等于圆上任意点M(x, y)与圆心A (a,b) 的距离.
符合上述条件的点M(x, y)集合是什么?你能用描述法来表示这个集合吗?
x
O
y
M
r
(x, y)
A
(a,b)
探究二:
圆上任意点M(x, y)与圆心A (a,b)之间的距离能用什么公式表示?
根据两点间距离公式:
则点M、A间的距离为:
即:
问:方程 一定表示圆吗?
方程有什么特点呢?
圆心在坐标原点,半径长为r 的圆的方程是什么?
因为圆心是原点O(0, 0),将x=0,y=0和半径 r 带入圆的标准方程:
得:
整理得:
探究三:
怎样判断点 在圆 内呢?还是在圆外呢?
可以看到:点在圆外——点到圆心的距离大于半径 r ;
点在圆内——点到圆心的距离小于半径 r .
x
y
o
M2
M1
M3
A
探究三:
点M(x0,y0)与圆C:(x-a)2+(y-b)2=r2的位置关系
位置关系
利用距离判断
利用方程判断
点M在圆上
|CM|=r
(x0-a)2+(y0-b)2=r2
点M在圆外
|CM|>r
(x0-a)2+(y0-b)2>r2
点M在圆内
|CM|
解:圆心是 ,半径长等于5的圆的标准方程是:
把 的坐标代入方程 左右两边相等,点 的坐标适合圆的方程,所以点
在这个圆上;
把点 的坐标代入此方程,左右两边不相等,点 的坐标不适合圆的方程,所以点 不在这个圆上.
待定系数法
解:设所求圆的方程为:
因为A(5,1),B (7,-3),C(2,8)都在圆上
所求圆的方程为
例2 ⊿ABC的三个顶点的坐标分别是A(5,1),
B(7,-3),C(2,-8),求它的外接圆的方程。
例3 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.
B
x
o
y
A
C
l
解:∵A(1,1),B(2,-2)
例3 己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的标准方程.
即:x-3y-3=0
∴圆心C(-3,-2)
方法2 设所求圆的标准方程为(x-a)2+(y-b)2=r2,
方法3 因为圆心在直线x-y+1=0上,
所以可设圆心C的坐标为(a,a+1).又因为|CA|=|CB|,
解得a=-3.
当堂检测
1
2
3
4
5
解析答案
C
解析答案
2.圆心是O(-3,4),半径长为5的圆的方程为( )
A.(x-3)2+(y+4)2=5
B.(x-3)2+(y+4)2=25
C.(x+3)2+(y-4)2=5
D.(x+3)2+(y-4)2=25
D
解析 将O(-3,4),r=5代入圆的标准方程可得.
1
2
3
4
5
1
2
3
4
5
解析答案
3.经过点(2,2),圆心为C(1,1)的圆的方程是( )
A.(x+1)2+(y+1)2=2
B.(x-1)2+(y-1)2=2
C.(x+1)2+(y+1)2=2
D.(x-1)2+(y-1)2=2
?
B
故圆的标准方程为(x-1)2+(y-1)2=2.
解析答案
4.点P(5a+1,12a)在圆(x-1)2+y2=1的外部,则a的取值范围为( )
D
1
2
3
4
5
1
2
3
4
5
解析答案
解析 由题意知圆C的圆心为(0,1),半径为1,
所以圆C的标准方程为x2+(y-1)2=1.
5.若圆C的半径为1,其圆心与点(1,0)关于直线y=x对称,则圆C的标准方程为_______________.
x2+(y-1)2=1
题型探究 重点突破
6.已知圆过两点A(3,1),B(-1,3),且它的圆心在直线3x-y-2=0上,求此圆的标准方程.
解析答案
反思与感悟
解 方法一 设所求圆的标准方程为(x-a)2+(y-b)2=r2,
解析答案
反思与感悟
故所求圆的标准方程为(x-2)2+(y-4)2=10.
所以线段AB的垂直平分线m的斜率为2.
解析答案
反思与感悟
因此直线m的方程为y-2=2(x-1),
即2x-y=0.
又因为圆心在直线3x-y-2=0上,
所以圆心是这两条直线的交点.
设圆心为C,所以圆心坐标为(2,4).
反思与感悟
所以所求圆的标准方程为(x-2)2+(y-4)2=10.
方法三 设圆心为C.
因为圆心在直线3x-y-2=0上,
所以可设圆心C的坐标为(a,3a-2).
又因为|CA|=|CB|,
解得a=2.
故所求圆的标准方程为(x-2)2+(y-4)2=10.
课堂小结
1.确定圆的方程主要方法是待定系数法,即列出关于a,b,r的方程组求a,b,r或直接求出圆心(a,b)和半径r.另外依据题意适时运用圆的几何性质解题可以化繁为简,提高解题效率.
2.讨论点与圆的位置关系可以从代数特征(点的坐标是否满足圆的方程)或几何特征(点到圆心的距离与半径的关系)去考虑,其中利用几何特征较为直观、快捷.
返回
谢 谢
