6.1.3 面积和体积公式课件-湘教版必修3(19张PPT)
文档属性
| 名称 | 6.1.3 面积和体积公式课件-湘教版必修3(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 185.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 00:00:00 | ||
图片预览




文档简介
6.1.3 面积和体积公式
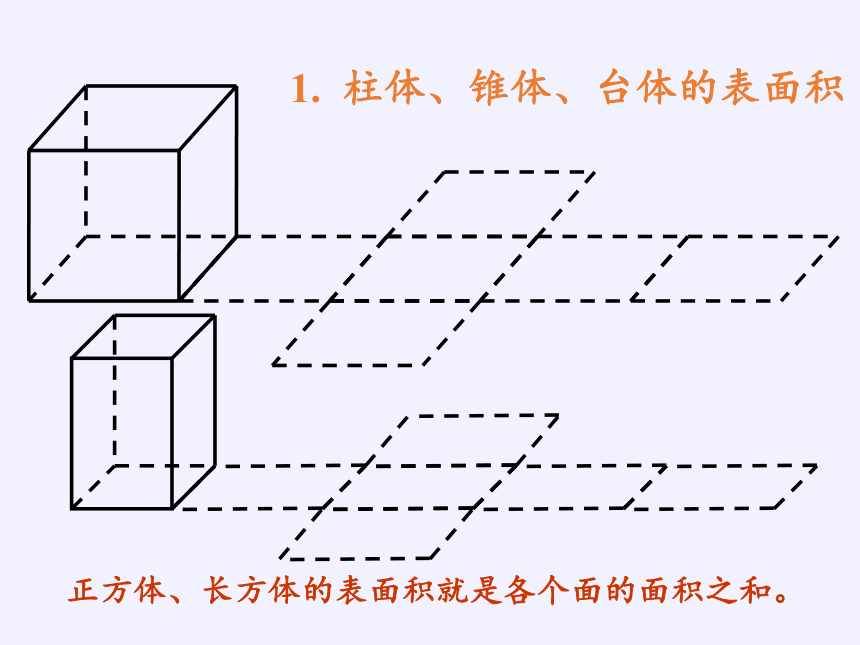
1. 柱体、锥体、台体的表面积
正方体、长方体的表面积就是各个面的面积之和。
探究
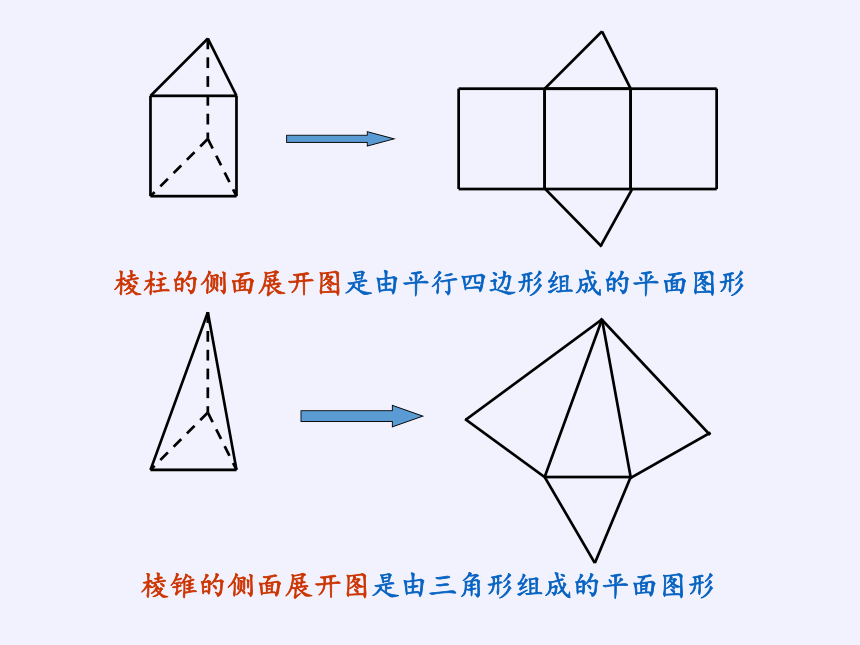
棱柱、棱锥、棱台也是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
棱柱的侧面展开图是由平行四边形组成的平面图形
棱锥的侧面展开图是由三角形组成的平面图形
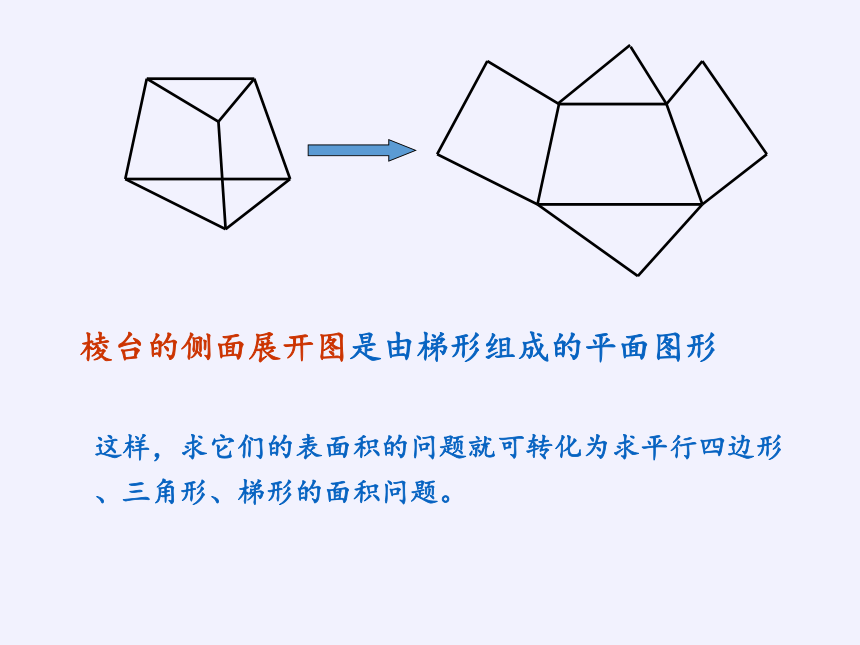
棱台的侧面展开图是由梯形组成的平面图形
这样,求它们的表面积的问题就可转化为求平行四边形、三角形、梯形的面积问题。
S
B
A
C
D
圆柱的侧面展开图是一个矩形:
如果圆柱的底面半径为 ,母线为 ,那么圆柱的底面积为 ,侧面积为 。因此圆柱的表面积为
O`
O
圆锥的侧面展开图是一个扇形:
如果圆柱的底面半径为 ,母线为
O
S
圆锥的表面积为:
那么圆锥的侧面积为:
圆台的侧面展开图是一个扇环,它的表面积等于上、下两个底面和加上侧面的面积,即
O`
O
思考:圆柱、圆锥、圆台的侧面积公式间的联系与区别
S圆柱侧= 2πrl
S圆锥侧= πrl
S圆台侧=π(r1+r2)l
r1=0
r1=r2
设球的半径为r,则表面积为:
球
例1:已知一个圆锥的底面半径为2,高为 。求圆锥的侧面积。
S
O
A
2
例2:以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于( )
A.2π B.π C.2 D.1
A
练习:如图是一个几何体的三视图,其中正视图和左视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
A.6π B.12π C.18π D.24π
B
15cm
10cm
7.5cm
小结:
这节课你收获了什么?
作业:
课本第21页练习题第1,2题
谢 谢
1. 柱体、锥体、台体的表面积
正方体、长方体的表面积就是各个面的面积之和。
探究
棱柱、棱锥、棱台也是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?
棱柱的侧面展开图是由平行四边形组成的平面图形
棱锥的侧面展开图是由三角形组成的平面图形
棱台的侧面展开图是由梯形组成的平面图形
这样,求它们的表面积的问题就可转化为求平行四边形、三角形、梯形的面积问题。
S
B
A
C
D
圆柱的侧面展开图是一个矩形:
如果圆柱的底面半径为 ,母线为 ,那么圆柱的底面积为 ,侧面积为 。因此圆柱的表面积为
O`
O
圆锥的侧面展开图是一个扇形:
如果圆柱的底面半径为 ,母线为
O
S
圆锥的表面积为:
那么圆锥的侧面积为:
圆台的侧面展开图是一个扇环,它的表面积等于上、下两个底面和加上侧面的面积,即
O`
O
思考:圆柱、圆锥、圆台的侧面积公式间的联系与区别
S圆柱侧= 2πrl
S圆锥侧= πrl
S圆台侧=π(r1+r2)l
r1=0
r1=r2
设球的半径为r,则表面积为:
球
例1:已知一个圆锥的底面半径为2,高为 。求圆锥的侧面积。
S
O
A
2
例2:以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于( )
A.2π B.π C.2 D.1
A
练习:如图是一个几何体的三视图,其中正视图和左视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
A.6π B.12π C.18π D.24π
B
15cm
10cm
7.5cm
小结:
这节课你收获了什么?
作业:
课本第21页练习题第1,2题
谢 谢
