6.2.1 点、线、面的位置关系课件-湘教版必修3(28张PPT)
文档属性
| 名称 | 6.2.1 点、线、面的位置关系课件-湘教版必修3(28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 12:25:12 | ||
图片预览








文档简介
6.2.1 点、线、面的位置关系
1.了解直线与平面之间的三种位置关系,会用符号语言和图形语言表示三种位置关系.(重点)
2.能用公理3解决一些简单的相关问题.
3.能用图形、文字、符号三种语言描述公理4.理解公理4的地位和作用.(难点)
4.了解定理1.(等角定理)(重点)
1.直线与平面的位置关系
有无数个公共点
a?α
有且只有一个公共点
a∩α=A
没有公共点
a∥α
平行
传递性
a∥c
3.公理4
(1)文字语言:如果两个不重合的平面有一个公共点,那么它们的交集是____________________.
(2)符号语言:P___α,且P∈β?α∩β=l,且P____l.
一条过该点的直线
∈
∈
4.定理1(等角定理)
(1)文字语言:空间中如果两个角的两条边分别对应________,那么这两个角相等或________.
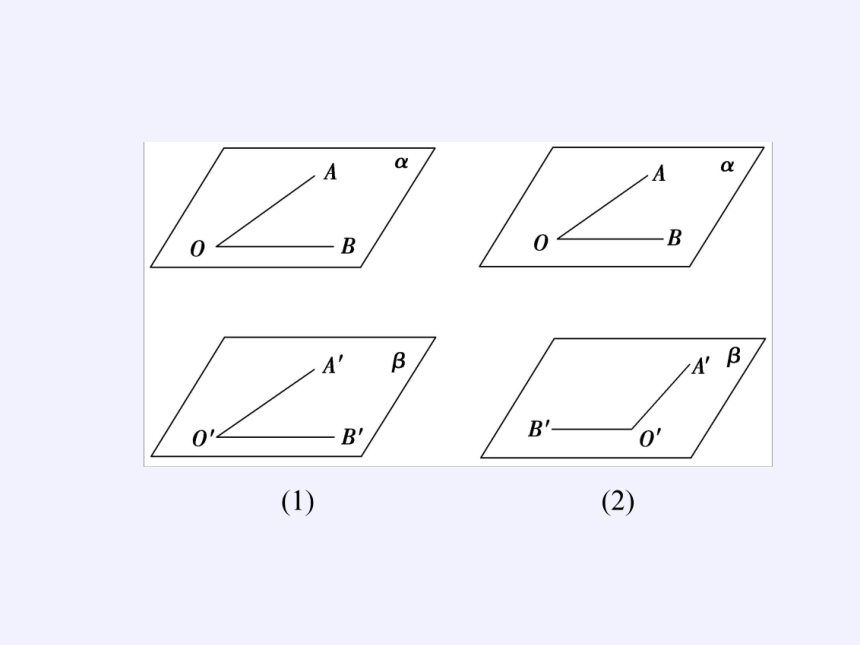
(2)符号语言:已知在∠AOB和∠A′O′B′中,AO∥A′O′,BO∥B′O′,则∠AOB=∠A′O′B′或∠AOB+∠A′O′B′=180°.如图(1)、(2)所示.
平行
互补
以下命题(其中a,b表示直线,α表示平面)①若a∥b,b?α,则a∥α;②若a∥α,b∥α,则a∥b;③若a∥b,b∥α,则a∥α;④若a∥α,b?α,则a∥b.其中正确命题的个数是( )
A.0个 B.1个
C.2个 D.3个
直线和平面的位置关系
解析:如图,在长方体ABCD—A′B′C′D′中,AB∥CD,AB?平面ABCD,但CD?平面ABCD,故①错误;
A′B′∥平面ABCD,B′C′∥平面ABCD,但A′B′与B′C′相交,故②错误;
AB∥A′B′,A′B′∥平面ABCD,但AB?平面ABCD,故③错误;
A′B′∥平面ABCD,BC?平面ABCD,但A′B′与BC异面,故④错误.
答案:A
空间直线与平面的位置关系的分类是问题求解的突破口,这类判断问题,常用分类讨论的方法解决.另外,借助模型(如长方体)也是解决这类问题的有效方法.
1.对于任意的直线l和平面α,在平面α内必有直线m,使m和l( )
A.平行 B.相交
C.垂直 D.异面
解析:若l∥α,则直线l与平面α无公共点,因此,直线l与平面α内的直线无公共点,即直线l与平面α内的所有直线均不相交;若l?α,则直线l和平面α内的直线共面,因此,直线l与平面α内的所有直线不能是异面直线;若l∩α=A,则直线l和平面α内的直线相交或异面,因此,直线l与平面α内的所有直线不平行.所以选项A,B,D都不正确.故选C.
答案:C
已知棱长为a的正方体ABCD-A′B′C′D′中,M,N分别为CD、AD的中点.求证:四边形MNA′C′是梯形.
公理3的应用
1.解答本题易出现“只证MN∥A′C′”,而忽视“证明MN≠A′C′”的错误.
2.公理3是证明两直线平行的重要方法,应用的关键在于寻找与所证直线平行的“中间直线”.
如图所示,已知E,E1分别是正方体ABCD-A1B1C1D1的棱AD,A1D1的中点,
求证:∠C1E1B1=∠CEB.
等角定理的应用
∴四边形E1EBB1为平行四边形,
∴E1B1∥EB.
同理E1C1∥EC.
又∠C1E1B1与∠CEB的对应边方向相同,
∴∠C1E1B1=∠CEB.
1.本题易出现漏掉“对应边方向相同”这样的错误.
2.利用空间等角定理证明两角相等时,一要说明两角的对应边分别平行;二要说明两角的方向相同.
正方体ABCD-A1B1C1D1不变,其他条件改为E、F、G分别是棱CC1、BB1、DD1中点.求证:∠BGC=∠FD1E.
1.直线与平面的位置关系有且只有三种:
直线在平面内、直线与平面相交、直线与平面平行.
后面两种关系又统称为直线在平面外.
2.证明空间两条直线平行的方法有两个:一是利用平面几何知识(三角形、梯形的中位线、平行四边形性质、平行线分线段成比例定理等)证明;二是利用公理3,就是需要找到第三条直线c,证a∥c,b∥c,由公理3得到a∥b.
3.证明两角相等,一般采用下面三种途径:
(1)三角形全等与相似.
(2)平行四边形的对角线或平行线与第三条直线相交所得内错角、同位角.
(3)等角定理.
谢 谢
1.了解直线与平面之间的三种位置关系,会用符号语言和图形语言表示三种位置关系.(重点)
2.能用公理3解决一些简单的相关问题.
3.能用图形、文字、符号三种语言描述公理4.理解公理4的地位和作用.(难点)
4.了解定理1.(等角定理)(重点)
1.直线与平面的位置关系
有无数个公共点
a?α
有且只有一个公共点
a∩α=A
没有公共点
a∥α
平行
传递性
a∥c
3.公理4
(1)文字语言:如果两个不重合的平面有一个公共点,那么它们的交集是____________________.
(2)符号语言:P___α,且P∈β?α∩β=l,且P____l.
一条过该点的直线
∈
∈
4.定理1(等角定理)
(1)文字语言:空间中如果两个角的两条边分别对应________,那么这两个角相等或________.
(2)符号语言:已知在∠AOB和∠A′O′B′中,AO∥A′O′,BO∥B′O′,则∠AOB=∠A′O′B′或∠AOB+∠A′O′B′=180°.如图(1)、(2)所示.
平行
互补
以下命题(其中a,b表示直线,α表示平面)①若a∥b,b?α,则a∥α;②若a∥α,b∥α,则a∥b;③若a∥b,b∥α,则a∥α;④若a∥α,b?α,则a∥b.其中正确命题的个数是( )
A.0个 B.1个
C.2个 D.3个
直线和平面的位置关系
解析:如图,在长方体ABCD—A′B′C′D′中,AB∥CD,AB?平面ABCD,但CD?平面ABCD,故①错误;
A′B′∥平面ABCD,B′C′∥平面ABCD,但A′B′与B′C′相交,故②错误;
AB∥A′B′,A′B′∥平面ABCD,但AB?平面ABCD,故③错误;
A′B′∥平面ABCD,BC?平面ABCD,但A′B′与BC异面,故④错误.
答案:A
空间直线与平面的位置关系的分类是问题求解的突破口,这类判断问题,常用分类讨论的方法解决.另外,借助模型(如长方体)也是解决这类问题的有效方法.
1.对于任意的直线l和平面α,在平面α内必有直线m,使m和l( )
A.平行 B.相交
C.垂直 D.异面
解析:若l∥α,则直线l与平面α无公共点,因此,直线l与平面α内的直线无公共点,即直线l与平面α内的所有直线均不相交;若l?α,则直线l和平面α内的直线共面,因此,直线l与平面α内的所有直线不能是异面直线;若l∩α=A,则直线l和平面α内的直线相交或异面,因此,直线l与平面α内的所有直线不平行.所以选项A,B,D都不正确.故选C.
答案:C
已知棱长为a的正方体ABCD-A′B′C′D′中,M,N分别为CD、AD的中点.求证:四边形MNA′C′是梯形.
公理3的应用
1.解答本题易出现“只证MN∥A′C′”,而忽视“证明MN≠A′C′”的错误.
2.公理3是证明两直线平行的重要方法,应用的关键在于寻找与所证直线平行的“中间直线”.
如图所示,已知E,E1分别是正方体ABCD-A1B1C1D1的棱AD,A1D1的中点,
求证:∠C1E1B1=∠CEB.
等角定理的应用
∴四边形E1EBB1为平行四边形,
∴E1B1∥EB.
同理E1C1∥EC.
又∠C1E1B1与∠CEB的对应边方向相同,
∴∠C1E1B1=∠CEB.
1.本题易出现漏掉“对应边方向相同”这样的错误.
2.利用空间等角定理证明两角相等时,一要说明两角的对应边分别平行;二要说明两角的方向相同.
正方体ABCD-A1B1C1D1不变,其他条件改为E、F、G分别是棱CC1、BB1、DD1中点.求证:∠BGC=∠FD1E.
1.直线与平面的位置关系有且只有三种:
直线在平面内、直线与平面相交、直线与平面平行.
后面两种关系又统称为直线在平面外.
2.证明空间两条直线平行的方法有两个:一是利用平面几何知识(三角形、梯形的中位线、平行四边形性质、平行线分线段成比例定理等)证明;二是利用公理3,就是需要找到第三条直线c,证a∥c,b∥c,由公理3得到a∥b.
3.证明两角相等,一般采用下面三种途径:
(1)三角形全等与相似.
(2)平行四边形的对角线或平行线与第三条直线相交所得内错角、同位角.
(3)等角定理.
谢 谢
