6.1.1几类简单的几何体_课件-湘教版必修3(34张PPT)
文档属性
| 名称 | 6.1.1几类简单的几何体_课件-湘教版必修3(34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 00:00:00 | ||
图片预览




文档简介
几类简单的几何体
【课标要求】
1.通过观察实例,了解柱、锥、台、球的定义,掌握柱、锥、台、球的结构特征及其关系.
2.在描述和判断几何结构特征的过程中,培养学生的观察能力和空间想象能力.
平面多边形
多边形
公共边
公共点
定直线
多面体
结构特征
图形
表示法
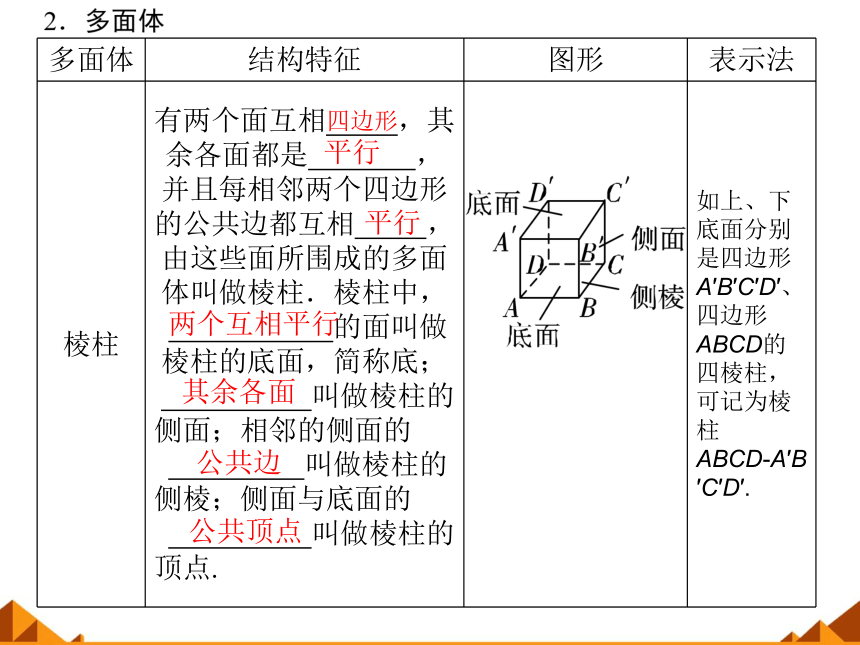
棱柱
有两个面互相 ,其余各面都是 ,并且每相邻两个四边形的公共边都互相 ,由这些面所围成的多面体叫做棱柱.棱柱中, . 的面叫做棱柱的底面,简称底;
. 叫做棱柱的侧面;相邻的侧面的 . . 叫做棱柱的侧棱;侧面与底面的 . 叫做棱柱的顶点.
如上、下底面分别是四边形A′B′C′D′、四边形ABCD的四棱柱,可记为棱柱ABCD?A′B′C′D′.
平行
四边形
平行
两个互相平行
其余各面
公共边
公共顶点
多面体
结构特征
图形
表示法
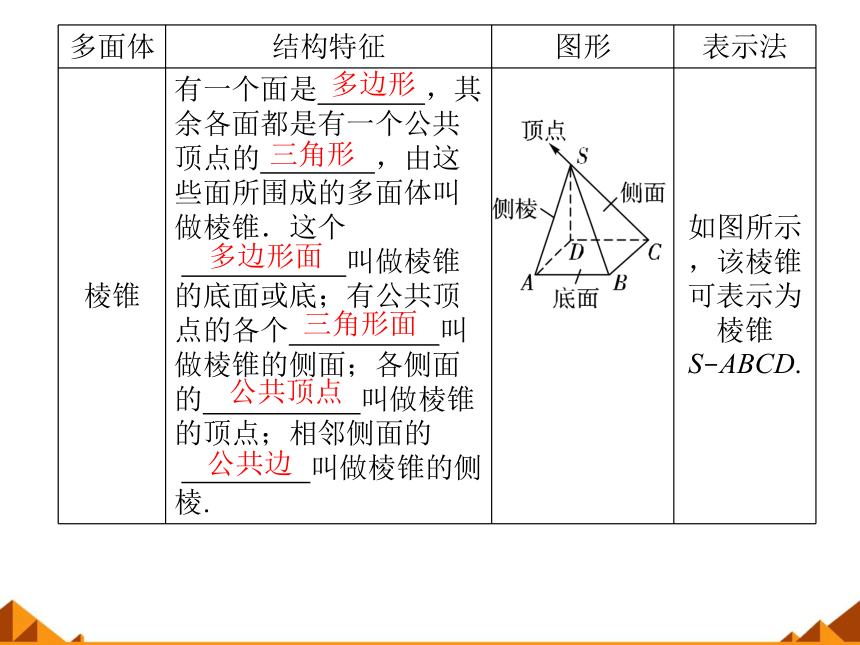
棱锥
有一个面是 ,其余各面都是有一个公共顶点的 ,由这些面所围成的多面体叫做棱锥.这个 . 叫做棱锥的底面或底;有公共顶点的各个 叫做棱锥的侧面;各侧面的 叫做棱锥的顶点;相邻侧面的 . 叫做棱锥的侧棱.
如图所示,该棱锥可表示为棱锥S?ABCD.
多边形
三角形
多边形面
三角形面
公共顶点
公共边
续表
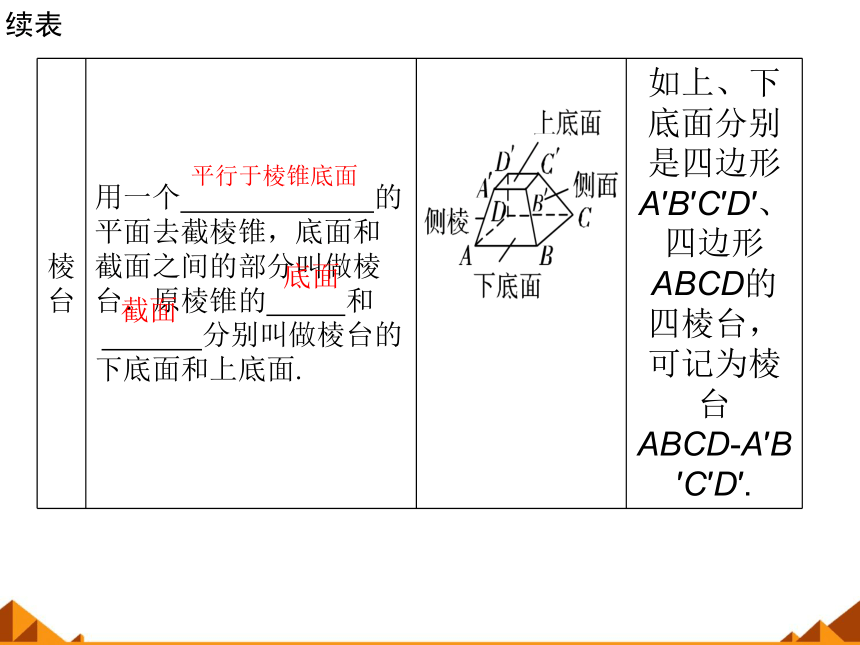
棱台
用一个 的平面去截棱锥,底面和截面之间的部分叫做棱台.原棱锥的 和 . 分别叫做棱台的下底面和上底面.
如上、下底面分别是四边形A′B′C′D′、四边形ABCD的四棱台,可记为棱台ABCD?A′B′C′D′.
平行于棱锥底面
底面
截面
3.旋转体
旋转体
结构特征
图形
表示法
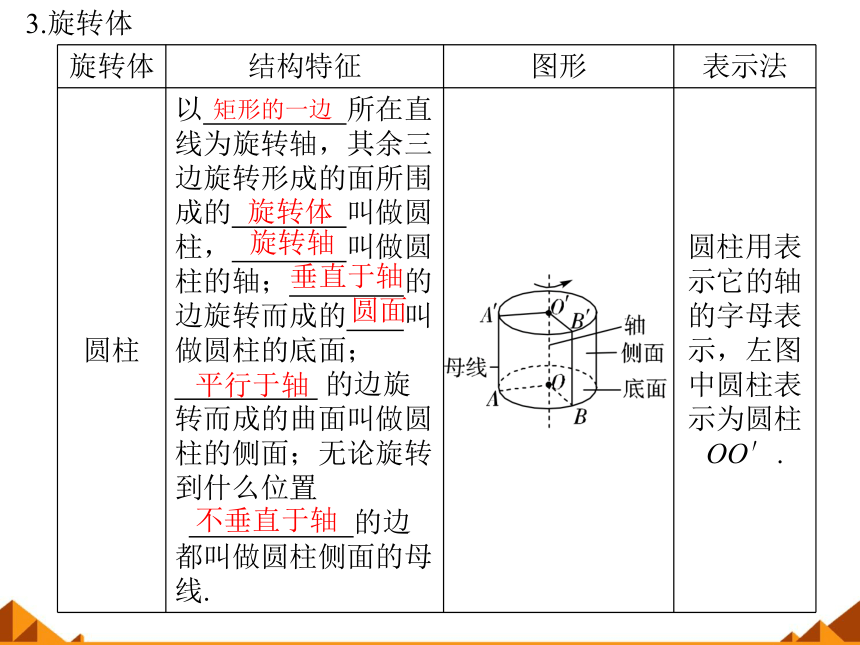
圆柱
以 所在直线为旋转轴,其余三边旋转形成的面所围成的 叫做圆柱, 叫做圆柱的轴; 的边旋转而成的 叫做圆柱的底面;
.的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置 . 的边都叫做圆柱侧面的母线.
圆柱用表示它的轴的字母表示,左图中圆柱表示为圆柱OO′.
矩形的一边
旋转体
旋转轴
垂直于轴
圆面
平行于轴
不垂直于轴
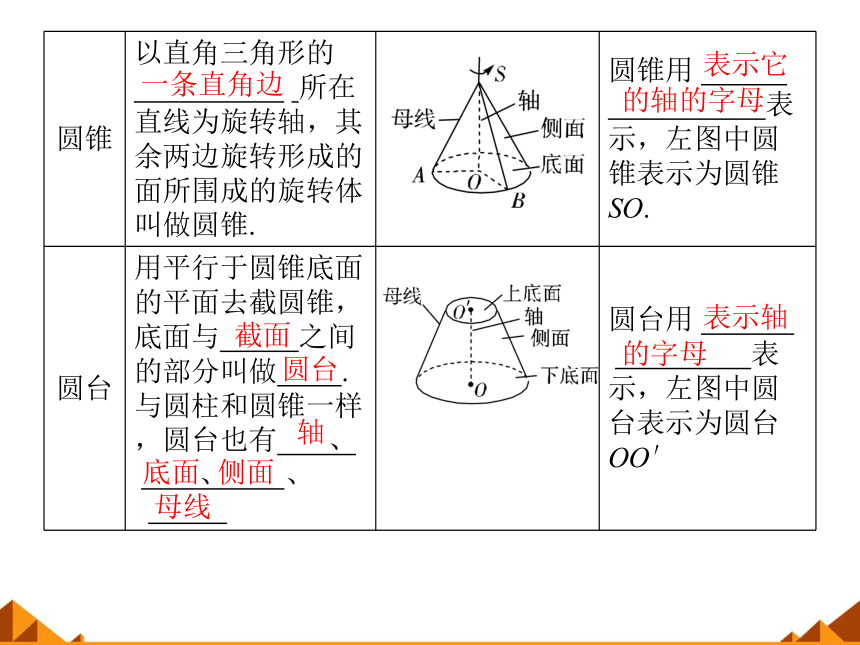
圆锥
以直角三角形的
. 所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥.
圆锥用. .
表示,左图中圆锥表示为圆锥SO.
圆台
用平行于圆锥底面的平面去截圆锥,底面与 之间的部分叫做 . 与圆柱和圆锥一样,圆台也有 、 . 、 、 . ..
圆台用. .
. 表示,左图中圆台表示为圆台OO′
一条直角边
截面
圆台
底面
侧面
母线
表示它
的轴的字母
表示轴
的字母
轴
续表
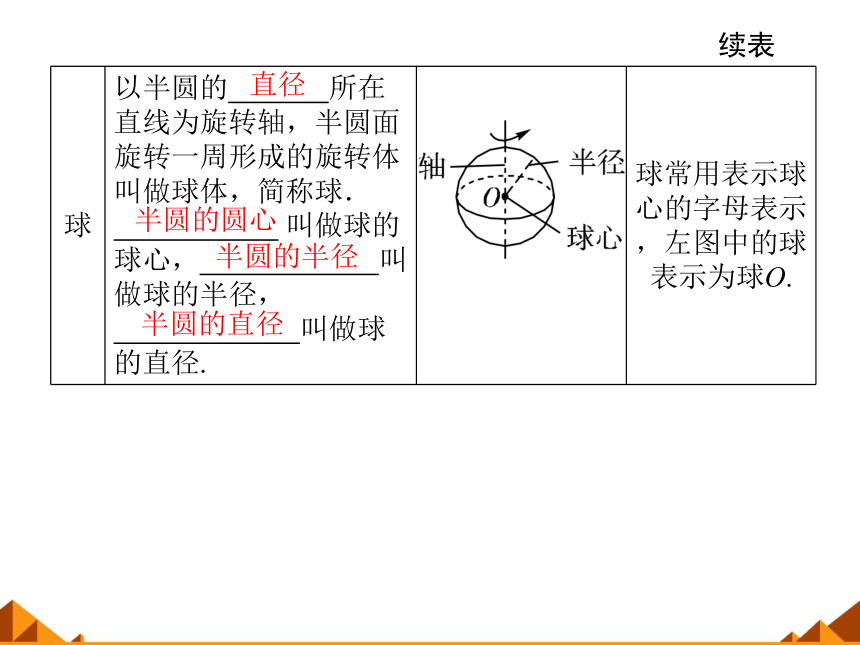
球
以半圆的 所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球.
.叫做球的球心, 叫做球的半径,
叫做球的直径.
球常用表示球心的字母表示,左图中的球表示为球O.
直径
半圆的圆心
半圆的半径
半圆的直径
自主探究
2.以钝角三角形的较小边所在直线为轴,其他两边旋转一周所得到的几何体是( ).
A.两个圆锥拼接而成的组合体
B.一个圆台
C.一个圆锥
D.一个圆锥挖去一个同底的小圆锥
3.一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为________ cm.
解析 n棱柱有2n个顶点,于是知此棱柱为五棱柱,故有5条侧棱.又每条侧棱长都相等,且和为60 cm,可知每条侧棱长为12 cm.
答案 12
4.在正方体上任意选择4个顶点,它们可能是如下各种几何体的4个顶点,这些几何体是________(写出所有正确结论的编号).
①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体.
解析 根据正方体的特点可知①③④正确,②不正确.
答案 ①③④
2.正棱锥中的有关概念
(1)正棱锥是指底面是正多边形,顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥,正棱锥的各个侧面都是等腰三角形,如图所示,为正四棱锥V—ABCD.
【训练2】 以下命题正确的是( ).
A.直角三角形绕一边所在直线旋转得到的旋转体是圆锥
B.夹在圆柱的两个平行截面间的几何体还是圆柱
C.圆锥截去一个小圆锥后剩余部分是圆台
D.绕直角梯形一腰所在直线旋转一周所得的几何体是圆台
解析 由圆锥、圆柱、圆台的形成过程可知,A、B、D不正确,C正确.
答案 C
解析 由图形旋转可得一个球体中间挖去一个圆柱.
答案 B
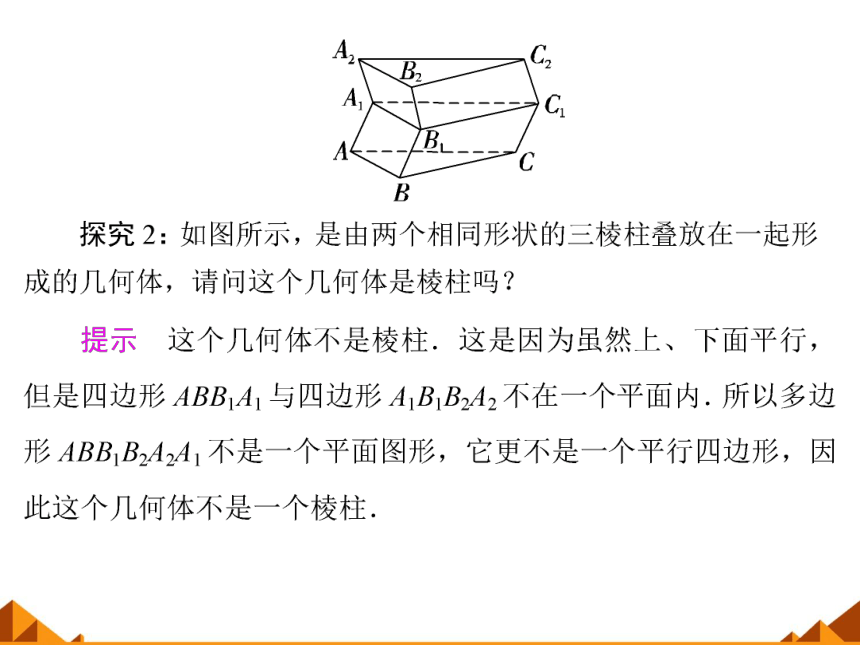
[正解] 图甲中的六个三角形没有一个公共点,故不是棱锥,只是一个多面体;图乙不是棱台,因为侧棱的延长线不能相交于同一点;图丙不是圆柱,因为上、下两面不平行(或不是由一个矩形旋转而成);图丁不是由一个直角三角形旋转而成,故不是圆锥.
纠错心得 解此类问题应结合常见几何体的定义和特征,分析所给几何体的结构特征,这就要求我们掌握常见几何体的结构特征.
3.要正确区分斜棱柱、直棱柱和正棱柱、长方体与正方体的关系,正确区分正三棱锥与正四面体的关系.
【课标要求】
1.通过观察实例,了解柱、锥、台、球的定义,掌握柱、锥、台、球的结构特征及其关系.
2.在描述和判断几何结构特征的过程中,培养学生的观察能力和空间想象能力.
平面多边形
多边形
公共边
公共点
定直线
多面体
结构特征
图形
表示法
棱柱
有两个面互相 ,其余各面都是 ,并且每相邻两个四边形的公共边都互相 ,由这些面所围成的多面体叫做棱柱.棱柱中, . 的面叫做棱柱的底面,简称底;
. 叫做棱柱的侧面;相邻的侧面的 . . 叫做棱柱的侧棱;侧面与底面的 . 叫做棱柱的顶点.
如上、下底面分别是四边形A′B′C′D′、四边形ABCD的四棱柱,可记为棱柱ABCD?A′B′C′D′.
平行
四边形
平行
两个互相平行
其余各面
公共边
公共顶点
多面体
结构特征
图形
表示法
棱锥
有一个面是 ,其余各面都是有一个公共顶点的 ,由这些面所围成的多面体叫做棱锥.这个 . 叫做棱锥的底面或底;有公共顶点的各个 叫做棱锥的侧面;各侧面的 叫做棱锥的顶点;相邻侧面的 . 叫做棱锥的侧棱.
如图所示,该棱锥可表示为棱锥S?ABCD.
多边形
三角形
多边形面
三角形面
公共顶点
公共边
续表
棱台
用一个 的平面去截棱锥,底面和截面之间的部分叫做棱台.原棱锥的 和 . 分别叫做棱台的下底面和上底面.
如上、下底面分别是四边形A′B′C′D′、四边形ABCD的四棱台,可记为棱台ABCD?A′B′C′D′.
平行于棱锥底面
底面
截面
3.旋转体
旋转体
结构特征
图形
表示法
圆柱
以 所在直线为旋转轴,其余三边旋转形成的面所围成的 叫做圆柱, 叫做圆柱的轴; 的边旋转而成的 叫做圆柱的底面;
.的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置 . 的边都叫做圆柱侧面的母线.
圆柱用表示它的轴的字母表示,左图中圆柱表示为圆柱OO′.
矩形的一边
旋转体
旋转轴
垂直于轴
圆面
平行于轴
不垂直于轴
圆锥
以直角三角形的
. 所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥.
圆锥用. .
表示,左图中圆锥表示为圆锥SO.
圆台
用平行于圆锥底面的平面去截圆锥,底面与 之间的部分叫做 . 与圆柱和圆锥一样,圆台也有 、 . 、 、 . ..
圆台用. .
. 表示,左图中圆台表示为圆台OO′
一条直角边
截面
圆台
底面
侧面
母线
表示它
的轴的字母
表示轴
的字母
轴
续表
球
以半圆的 所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球.
.叫做球的球心, 叫做球的半径,
叫做球的直径.
球常用表示球心的字母表示,左图中的球表示为球O.
直径
半圆的圆心
半圆的半径
半圆的直径
自主探究
2.以钝角三角形的较小边所在直线为轴,其他两边旋转一周所得到的几何体是( ).
A.两个圆锥拼接而成的组合体
B.一个圆台
C.一个圆锥
D.一个圆锥挖去一个同底的小圆锥
3.一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为________ cm.
解析 n棱柱有2n个顶点,于是知此棱柱为五棱柱,故有5条侧棱.又每条侧棱长都相等,且和为60 cm,可知每条侧棱长为12 cm.
答案 12
4.在正方体上任意选择4个顶点,它们可能是如下各种几何体的4个顶点,这些几何体是________(写出所有正确结论的编号).
①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体.
解析 根据正方体的特点可知①③④正确,②不正确.
答案 ①③④
2.正棱锥中的有关概念
(1)正棱锥是指底面是正多边形,顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥,正棱锥的各个侧面都是等腰三角形,如图所示,为正四棱锥V—ABCD.
【训练2】 以下命题正确的是( ).
A.直角三角形绕一边所在直线旋转得到的旋转体是圆锥
B.夹在圆柱的两个平行截面间的几何体还是圆柱
C.圆锥截去一个小圆锥后剩余部分是圆台
D.绕直角梯形一腰所在直线旋转一周所得的几何体是圆台
解析 由圆锥、圆柱、圆台的形成过程可知,A、B、D不正确,C正确.
答案 C
解析 由图形旋转可得一个球体中间挖去一个圆柱.
答案 B
[正解] 图甲中的六个三角形没有一个公共点,故不是棱锥,只是一个多面体;图乙不是棱台,因为侧棱的延长线不能相交于同一点;图丙不是圆柱,因为上、下两面不平行(或不是由一个矩形旋转而成);图丁不是由一个直角三角形旋转而成,故不是圆锥.
纠错心得 解此类问题应结合常见几何体的定义和特征,分析所给几何体的结构特征,这就要求我们掌握常见几何体的结构特征.
3.要正确区分斜棱柱、直棱柱和正棱柱、长方体与正方体的关系,正确区分正三棱锥与正四面体的关系.
