6.2.1点、线、面的位置关系_课件1(1)-湘教版必修3(32张PPT)
文档属性
| 名称 | 6.2.1点、线、面的位置关系_课件1(1)-湘教版必修3(32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 12:26:19 | ||
图片预览











文档简介
点、线、面的位置关系
有无数个公共点
有且只有一个
公共点
a?α
a∩α=A
没有公共点
a∥α
平行
传递性
a∥c
公共直线
∈
l
∈
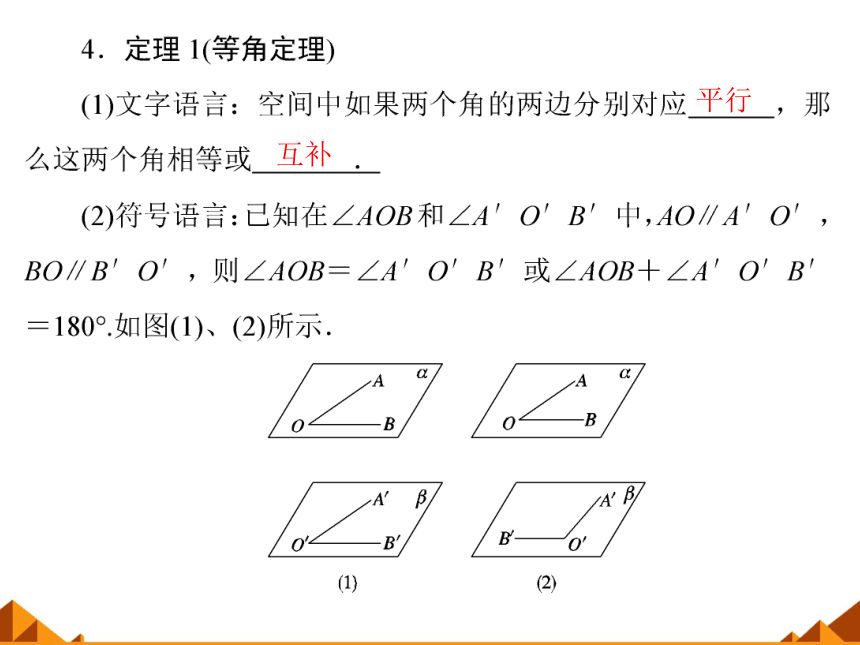
平行
互补
预习测评
1.过平面外一点,可作这个平面的平行线条数为( ).
A.1条 B.2条
C.无数条 D.不确定
解析 两平行平面,过其一平面内任一点可作无数条直
线与另一平面无交点,即平行.
答案 C
2.将“如果两个不重合的平面α、β有一个公共点P,那么它们有且只有一条过该点的公共直线l.”改写成符号语言表述应为________.
解析 ∵两个不重合的平面α,β有一个公共点P,
∴P∈α∩β,又P点在平面α、β的交线l上,
∴α∩β=l且P∈l.
答案 P∈α∩β?α∩β=l且P∈l
3.在四面体ABCD的边AB、BC、CD、DA上分别取E、F、G、H四点,如果EF∩GH=P,则点P一定在直线________上.
解析 ∵EF∩GH=P,EF?平面ABC,
∴P∈平面ABC.
又GH?平面ACD,∴P∈平面ACD.
∵平面ABC∩平面ACD=AC,
∴P∈AC.
答案 AC
解析 (1)B1D1∥BD,B1C1∥BC并且方向相同,所以∠DBC的两边与∠D1B1C1的两边分别对应平行且方向相同.
(2)D1B1∥BD,D1A1∥BC并且方向相反,所以∠DBC的两边与∠B1D1A1的两边分别对应平行且方向相反.
答案 (1)D1B1C1 (2)B1D1A1
2.公理3
(1)公理3是用来证明两条直线平行的依据之一.
(2)公理3可理解为直线间平行关系的传递性.
3.公理4
公理4的作用:公理4主要说明了两个相交平面的特征,对我们确定两个平面的交线有着重要的作用.
其一,它是判定两个平面是否相交的依据,也就是说,只要两个平面有公共点,则这两个平面就相交;其二,它可以证多点共线的问题.若点是某两个平面的公共点,则该点必定在这两个平面的交线上.
(2)在画直线a与平面α相交时,表示直线a的直线必须有部分在表示平面α的平行四边形之外,这样做既能与表示直线在平面内的图形区分开来,又使之具有较强的立体感,注意此时被平面遮住的部分必须画成虚线.
(3)画直线与平面平行时,最直观的图形是表示直线的直线画在表示平面的平行四边形之外,且与某一边平行.
【训练1】 作出下列各小题的图形.
(1)画直线a、b,使a∩α=A,b∥α;
(2)画平面α、β,直线a、b,使α∩β=l,a?α,b?β,且a∥β,b∩α=B.
方法点评 证明两直线平行的方法:
①平行线的定义:在同一平面内没有公共点的两直线是平行直线.
②利用三角形中位线平行于底边这一性质.
③利用公理4.
④利用平行四边形对边互相平行的性质.
[正解] A
纠错心得 在研究直线与平面的位置关系时,一定要真正理解相关概念.实际上,直线与平面相交,要求直线与平面有且只有一个公共点,即直线与平面有一个公共点且直线不在平面内,也即直线既不与平面平行,又不在平面内.直线与平面不相交,即直线与平面平行,或者直线在平面内.
有无数个公共点
有且只有一个
公共点
a?α
a∩α=A
没有公共点
a∥α
平行
传递性
a∥c
公共直线
∈
l
∈
平行
互补
预习测评
1.过平面外一点,可作这个平面的平行线条数为( ).
A.1条 B.2条
C.无数条 D.不确定
解析 两平行平面,过其一平面内任一点可作无数条直
线与另一平面无交点,即平行.
答案 C
2.将“如果两个不重合的平面α、β有一个公共点P,那么它们有且只有一条过该点的公共直线l.”改写成符号语言表述应为________.
解析 ∵两个不重合的平面α,β有一个公共点P,
∴P∈α∩β,又P点在平面α、β的交线l上,
∴α∩β=l且P∈l.
答案 P∈α∩β?α∩β=l且P∈l
3.在四面体ABCD的边AB、BC、CD、DA上分别取E、F、G、H四点,如果EF∩GH=P,则点P一定在直线________上.
解析 ∵EF∩GH=P,EF?平面ABC,
∴P∈平面ABC.
又GH?平面ACD,∴P∈平面ACD.
∵平面ABC∩平面ACD=AC,
∴P∈AC.
答案 AC
解析 (1)B1D1∥BD,B1C1∥BC并且方向相同,所以∠DBC的两边与∠D1B1C1的两边分别对应平行且方向相同.
(2)D1B1∥BD,D1A1∥BC并且方向相反,所以∠DBC的两边与∠B1D1A1的两边分别对应平行且方向相反.
答案 (1)D1B1C1 (2)B1D1A1
2.公理3
(1)公理3是用来证明两条直线平行的依据之一.
(2)公理3可理解为直线间平行关系的传递性.
3.公理4
公理4的作用:公理4主要说明了两个相交平面的特征,对我们确定两个平面的交线有着重要的作用.
其一,它是判定两个平面是否相交的依据,也就是说,只要两个平面有公共点,则这两个平面就相交;其二,它可以证多点共线的问题.若点是某两个平面的公共点,则该点必定在这两个平面的交线上.
(2)在画直线a与平面α相交时,表示直线a的直线必须有部分在表示平面α的平行四边形之外,这样做既能与表示直线在平面内的图形区分开来,又使之具有较强的立体感,注意此时被平面遮住的部分必须画成虚线.
(3)画直线与平面平行时,最直观的图形是表示直线的直线画在表示平面的平行四边形之外,且与某一边平行.
【训练1】 作出下列各小题的图形.
(1)画直线a、b,使a∩α=A,b∥α;
(2)画平面α、β,直线a、b,使α∩β=l,a?α,b?β,且a∥β,b∩α=B.
方法点评 证明两直线平行的方法:
①平行线的定义:在同一平面内没有公共点的两直线是平行直线.
②利用三角形中位线平行于底边这一性质.
③利用公理4.
④利用平行四边形对边互相平行的性质.
[正解] A
纠错心得 在研究直线与平面的位置关系时,一定要真正理解相关概念.实际上,直线与平面相交,要求直线与平面有且只有一个公共点,即直线与平面有一个公共点且直线不在平面内,也即直线既不与平面平行,又不在平面内.直线与平面不相交,即直线与平面平行,或者直线在平面内.
