6.2.3直线与平面垂直的判定课件-湘教版必修3(24张PPT)
文档属性
| 名称 | 6.2.3直线与平面垂直的判定课件-湘教版必修3(24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 12:32:32 | ||
图片预览





文档简介
我们来感受
我们来回顾
我们来回顾
直线与平面垂直的判定
忠心爱国 精心求知诚心待人 恒心健体
目
标
Learning Target
知识与技能
通过直观感知、操作确认,理解线面垂直的定义,归纳线面垂直的判定定理, 并能运用定义和定理证明一些空间位置关系的简单命题。
过程与方法
通过线面垂直定义及定理的探究过程,感知几何直观能力和抽象概括能力,体会转化思想在解决问题中的运用。
情感、态度与价值观
通过线面垂直定义及定理的探究,让学生亲身经历数学研究的过程,体验探索的乐趣,增强学习数学的兴趣。
【思考】如何定义“直线与平面垂直”?
我们来感受
垂直
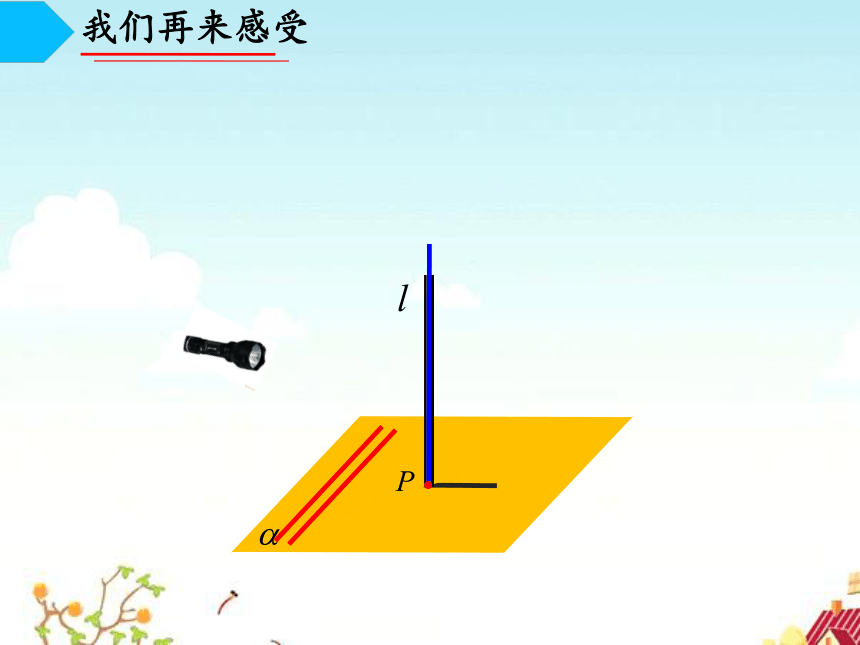
我们再来感受
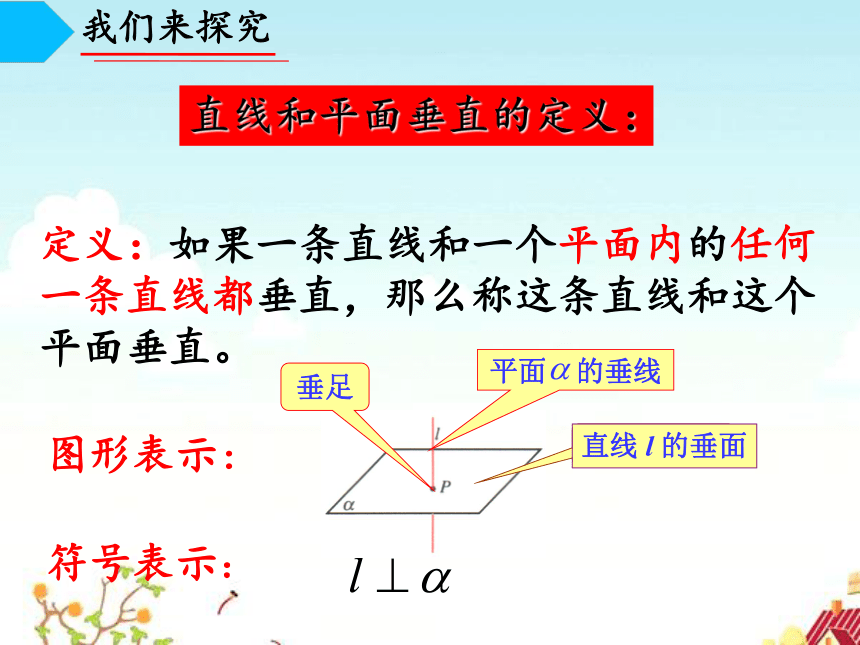
直线和平面垂直的定义:
定义:如果一条直线和一个平面内的任何一条直线都垂直,那么称这条直线和这个平面垂直。
符号表示:
图形表示:
平面 的垂线
直线 l 的垂面
垂足
我们来探究
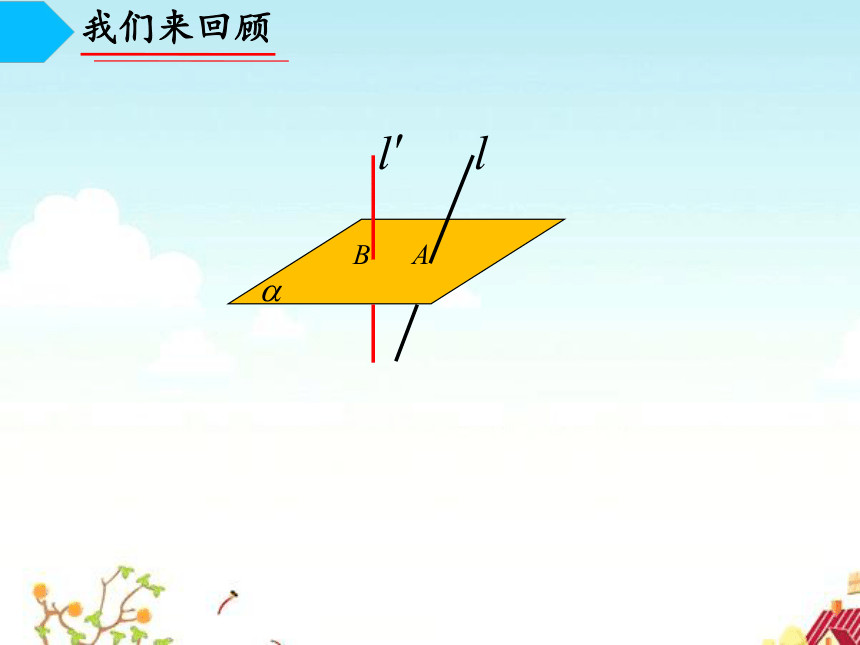
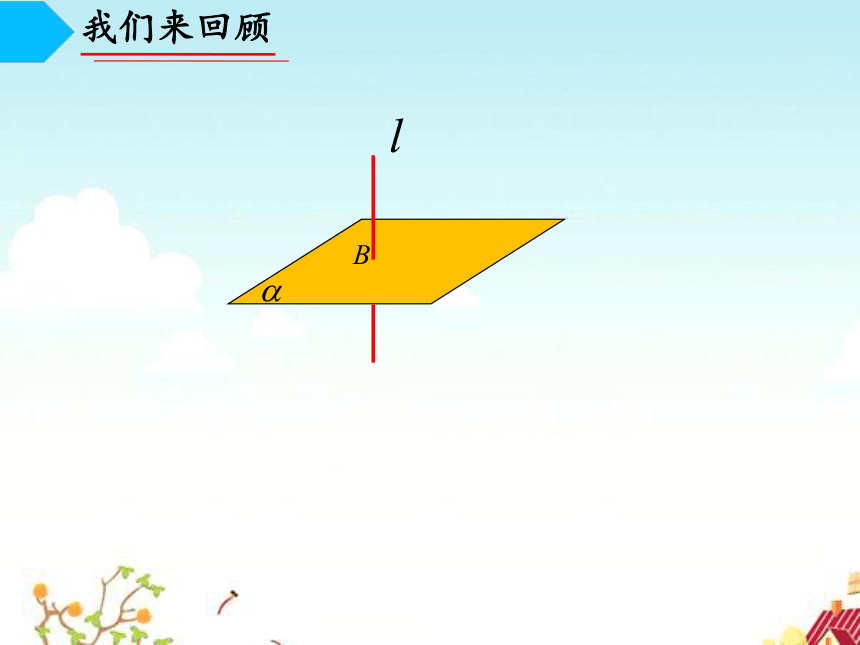
问题一:如果一条直线 垂直于一个平面 内的一条直线,能确定 吗 ?
我们来探究
问题二:如果一条直线 垂直于一个平面 内的两条直线,能确定 吗 ?
我们来探究
问题三:如果一条直线 垂直于一个平面 内的无数条直线,能确定 吗 ?
我们来探究
请准备一块三角形的纸片,过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触),请问:折痕AD与桌面垂直吗?
A
B
D
C
如何翻折才能使折痕AD与桌面垂直?
我们来探究
A
B
D
C
A
B
C
D
A
B
D
C
A
B
C
D
图1
图2
A
B
C
我们来探究
D
判定定理:
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
我们来发现
A
B
C
D
A1
B1
C1
D1
如图,在正方体 中
(1)你能找出与平面 垂直的直线吗?
(2)你能找出与直线 垂直的平面吗?
(3)你还能找出与平面 垂直的直线吗?
我们练一练
例1 如图, 是菱形 所在平面外一点, 为 与 的交点, ,求证:
证明:
M
A
B
C
D
O
连结
我们来巩固
A
B
C
D
E
例2 在三棱锥 中, 和 是边长 为2的正三角形, , 为 的中点,求证:
我们来巩固
A
B
C
D
E
例3(追问)在三棱锥 中, 和 是边长为2的正三角形, , 为 的中点,求证:
你还能发现其它的线面垂直关系吗?
我们来巩固
如图,直四棱柱 (侧棱与 底面垂直的棱柱成为直棱柱)中,底面四边形
满足什么条件时, ?(只能添加一个合适的条件)
解:底面ABCD可以是菱形,正方形, 或者是对角线相互垂直的任意四边形.
我们想一想
生活
现象
数学
知识
抽象
( 核 心 素 养 )
生活
运用
模型
?推理
我们共提高
2.判定线面垂直的方法:
(1)利用定义,证明这条直线和平面内的任
何一条直线垂直;
(2)利用判定定理,证明这条直线和平面内的两条相交直线垂直;
1.线面垂直的定义
共同点:
线线垂直
线面垂直
我们来小结
作
业
Homework
我们共努力
2.(选做)探究直线与平面
垂直的性质;
3.(校本)查阅资料,了解
直线与平面垂直的判定定理
的证明方法.
1.(必做)本P42第4,5题;
我们来回顾
我们来回顾
直线与平面垂直的判定
忠心爱国 精心求知诚心待人 恒心健体
目
标
Learning Target
知识与技能
通过直观感知、操作确认,理解线面垂直的定义,归纳线面垂直的判定定理, 并能运用定义和定理证明一些空间位置关系的简单命题。
过程与方法
通过线面垂直定义及定理的探究过程,感知几何直观能力和抽象概括能力,体会转化思想在解决问题中的运用。
情感、态度与价值观
通过线面垂直定义及定理的探究,让学生亲身经历数学研究的过程,体验探索的乐趣,增强学习数学的兴趣。
【思考】如何定义“直线与平面垂直”?
我们来感受
垂直
我们再来感受
直线和平面垂直的定义:
定义:如果一条直线和一个平面内的任何一条直线都垂直,那么称这条直线和这个平面垂直。
符号表示:
图形表示:
平面 的垂线
直线 l 的垂面
垂足
我们来探究
问题一:如果一条直线 垂直于一个平面 内的一条直线,能确定 吗 ?
我们来探究
问题二:如果一条直线 垂直于一个平面 内的两条直线,能确定 吗 ?
我们来探究
问题三:如果一条直线 垂直于一个平面 内的无数条直线,能确定 吗 ?
我们来探究
请准备一块三角形的纸片,过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触),请问:折痕AD与桌面垂直吗?
A
B
D
C
如何翻折才能使折痕AD与桌面垂直?
我们来探究
A
B
D
C
A
B
C
D
A
B
D
C
A
B
C
D
图1
图2
A
B
C
我们来探究
D
判定定理:
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.
我们来发现
A
B
C
D
A1
B1
C1
D1
如图,在正方体 中
(1)你能找出与平面 垂直的直线吗?
(2)你能找出与直线 垂直的平面吗?
(3)你还能找出与平面 垂直的直线吗?
我们练一练
例1 如图, 是菱形 所在平面外一点, 为 与 的交点, ,求证:
证明:
M
A
B
C
D
O
连结
我们来巩固
A
B
C
D
E
例2 在三棱锥 中, 和 是边长 为2的正三角形, , 为 的中点,求证:
我们来巩固
A
B
C
D
E
例3(追问)在三棱锥 中, 和 是边长为2的正三角形, , 为 的中点,求证:
你还能发现其它的线面垂直关系吗?
我们来巩固
如图,直四棱柱 (侧棱与 底面垂直的棱柱成为直棱柱)中,底面四边形
满足什么条件时, ?(只能添加一个合适的条件)
解:底面ABCD可以是菱形,正方形, 或者是对角线相互垂直的任意四边形.
我们想一想
生活
现象
数学
知识
抽象
( 核 心 素 养 )
生活
运用
模型
?推理
我们共提高
2.判定线面垂直的方法:
(1)利用定义,证明这条直线和平面内的任
何一条直线垂直;
(2)利用判定定理,证明这条直线和平面内的两条相交直线垂直;
1.线面垂直的定义
共同点:
线线垂直
线面垂直
我们来小结
作
业
Homework
我们共努力
2.(选做)探究直线与平面
垂直的性质;
3.(校本)查阅资料,了解
直线与平面垂直的判定定理
的证明方法.
1.(必做)本P42第4,5题;
