第7章 解析几何初步 复习课件-湘教版必修3(46张PPT)
文档属性
| 名称 | 第7章 解析几何初步 复习课件-湘教版必修3(46张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 00:00:00 | ||
图片预览










文档简介
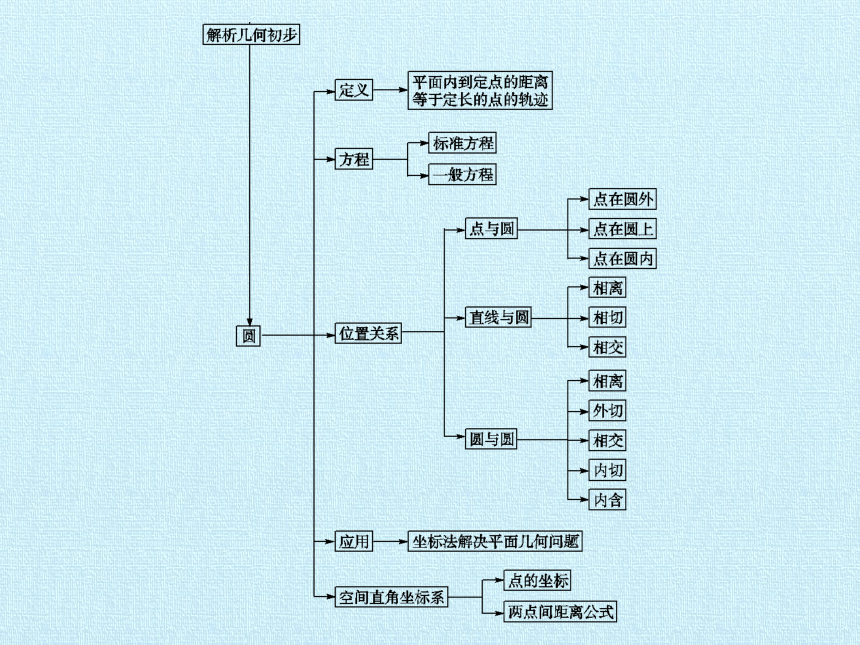
第7章 解析几何初步 复习课件
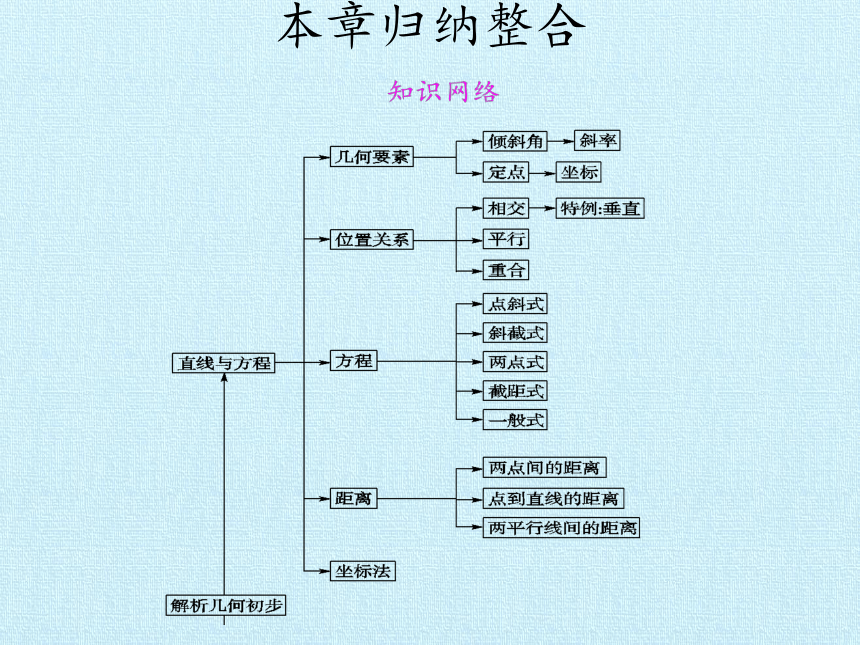
本章归纳整合
名称
方程
常数的几何意义
适用条件
点斜
式
y-y0=k(x-x0)
(x0,y0)是直线上的一个定点,k是斜率
直线不垂直于x轴
斜截
式
y=kx+b
k是斜率,b是直线在y轴上的截距
直线不垂直于x轴
两点
式
(y2-y1)(x-x1)-(x2-x1)·(y-y1)=0
(x1,y1),(x2,y2)是直线上的两个定点
任何情况
截距
式
a,b分别是直线在x轴,y轴上的非零截距
直线不垂直于x轴和y轴,且不过原点
一般
式
Ax+By+C=0,(A,B不同时为0)
A,B,C为系数
任何情况
名称
方程
常数的几何意义
适用条件
点斜
式
y-y0=k(x-x0)
(x0,y0)是直线上的一个定点,k是斜率
直线不垂直于x轴
斜截
式
y=kx+b
k是斜率,b是直线在y轴上的截距
直线不垂直于x轴
两点
式
(y2-y1)(x-x1)-(x2-x1)·(y-y1)=0
(x1,y1),(x2,y2)是直线上的两个定点
任何情况
位置关系
文字表示
符号表示
l1:y=k1x+b1
l2:y=k2x+b2
l1:A1x+B1y+C1=0
l2:A2x+B2y+C2=0
平行
斜率存在且不重合的两直线,如果它们的斜率相等,那么它们平行;反之亦然
l1∥l2?k1=k2,且b1≠b2
l1∥l2?
垂直
斜率存在的两直线,如果它们的斜率互为负倒数,那么它们垂直;反之亦然
l1⊥l2?k1k2=-1
l1⊥l2?A1A2+B1B2=0
谢 谢
本章归纳整合
名称
方程
常数的几何意义
适用条件
点斜
式
y-y0=k(x-x0)
(x0,y0)是直线上的一个定点,k是斜率
直线不垂直于x轴
斜截
式
y=kx+b
k是斜率,b是直线在y轴上的截距
直线不垂直于x轴
两点
式
(y2-y1)(x-x1)-(x2-x1)·(y-y1)=0
(x1,y1),(x2,y2)是直线上的两个定点
任何情况
截距
式
a,b分别是直线在x轴,y轴上的非零截距
直线不垂直于x轴和y轴,且不过原点
一般
式
Ax+By+C=0,(A,B不同时为0)
A,B,C为系数
任何情况
名称
方程
常数的几何意义
适用条件
点斜
式
y-y0=k(x-x0)
(x0,y0)是直线上的一个定点,k是斜率
直线不垂直于x轴
斜截
式
y=kx+b
k是斜率,b是直线在y轴上的截距
直线不垂直于x轴
两点
式
(y2-y1)(x-x1)-(x2-x1)·(y-y1)=0
(x1,y1),(x2,y2)是直线上的两个定点
任何情况
位置关系
文字表示
符号表示
l1:y=k1x+b1
l2:y=k2x+b2
l1:A1x+B1y+C1=0
l2:A2x+B2y+C2=0
平行
斜率存在且不重合的两直线,如果它们的斜率相等,那么它们平行;反之亦然
l1∥l2?k1=k2,且b1≠b2
l1∥l2?
垂直
斜率存在的两直线,如果它们的斜率互为负倒数,那么它们垂直;反之亦然
l1⊥l2?k1k2=-1
l1⊥l2?A1A2+B1B2=0
谢 谢
