对数与对数运算第一课时
图片预览




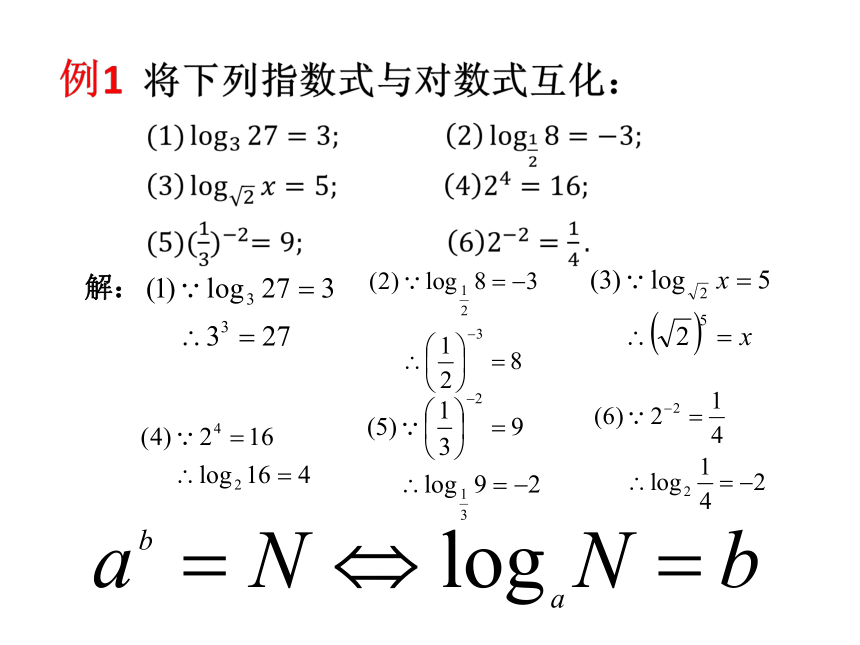

文档简介
(共19张PPT)
问题1:庄子:一尺之棰,日取其半,万世不竭,
①取4次还有多长?怎样计算?
②取多少次还有0.125尺
解:
假设2002年我国国民生产总值为a
亿元,如果每年平均增长8%,那么经
过多少年国民生产总值是2002年的2倍?
问题2
如何列方程?
如何求出x的值
即
这是已知底数和幂的值,求指数的问题。即指数式 中,已知a 和N.求b的问题。(这里 a>0且a≠1 )
一般地,如果a(a>0, 且a≠1)的b次幂
等于N,就是ab=N ,那么数b叫做以a为底
N的对数,记作logaN=b.其中a叫底数,
N叫真数.即
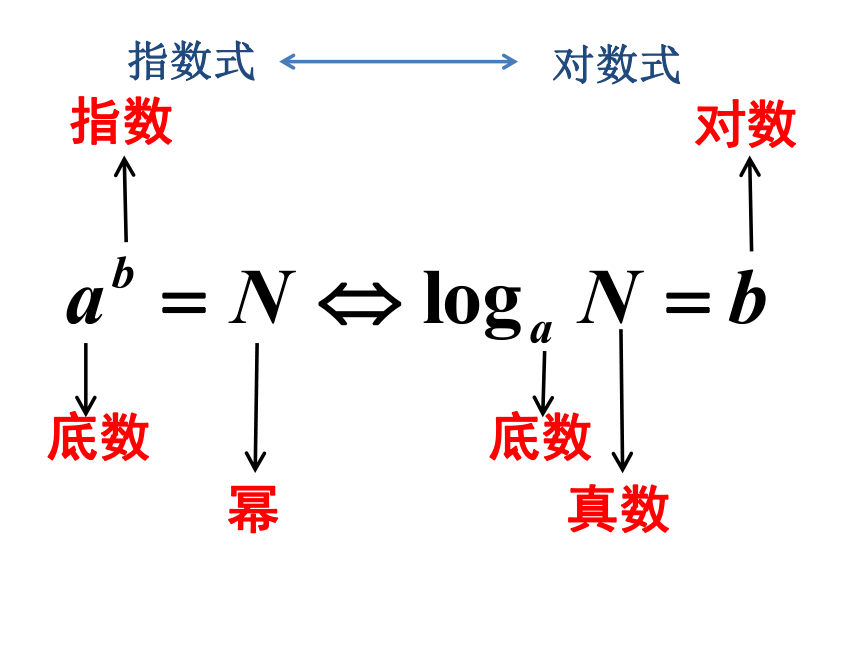
定义:
指数
真数
底数
对数
幂
底数
指数式
对数式
解:
1. 我们通常将以10为底的对数叫做常用对数. 为了简便,N的常用对数log10N简记作lgN.
2. 在科学技术中常常使用以无理数
e=2.71828……为底的对数,以e为底的对数叫自然对数,为了简便,N的自然对数logeN简记作lnN.
试试:分别说说lg5 、lg3.5、ln10、ln3的意义.
两种特殊的对数
(1)若a<0,则N取某些数值时,logaN不存在
因此,规定a不能小于0.
1.为什么对数logaN只有在a>0且a≠1时才有意义呢?
因此,规定a≠0.
探究一:
因此,规定a≠1
综上所述,对数符号logaN只有在a>0且a≠1时才有意义
由于正数的任何次幂都是正数,即ab>0
因此N>0.
底数a的取值范围(0, 1)∪(1, +∞);
真数N的取值范围(0, +∞).
2.负数和0有没有对数?
即 负数和0没有对数
探究一:
求log(1-x)(x+2)中的x的取值范围.
练习:
例2 求出下列各式中 x 值:
解:(1)
解:(2)
例2 求出下列各式中 x 值:
探究二:
loga1=?,logaa=?
loga1=0,logaa=1
练习:求下列各式x的值
解:
小结:
1.对数的定义(注意字母取值范围a>0,a≠1,N>0)
2.两个特殊对数(lgN,lnN)
3.两个等式: loga1=0,logaa=1
通过本节课的学习,你们有哪些收获?
4.应用指对数互化求值
思考:
作业:
1.必做题:第74页A组1,2
2.选做题:
(1)求对数式 中X的取值范围
(2)若 ,则X= 。
(3)计算: (a>0,b>0,c>0,N>0)
3.请同学们阅读课本,搜集有关对数发展材料,寻找有关换底公式材料,为下一步学习打基础。
谢谢!
思考:
解:成立。此式为对数恒等式。
练习:求值
解:
问题1:庄子:一尺之棰,日取其半,万世不竭,
①取4次还有多长?怎样计算?
②取多少次还有0.125尺
解:
假设2002年我国国民生产总值为a
亿元,如果每年平均增长8%,那么经
过多少年国民生产总值是2002年的2倍?
问题2
如何列方程?
如何求出x的值
即
这是已知底数和幂的值,求指数的问题。即指数式 中,已知a 和N.求b的问题。(这里 a>0且a≠1 )
一般地,如果a(a>0, 且a≠1)的b次幂
等于N,就是ab=N ,那么数b叫做以a为底
N的对数,记作logaN=b.其中a叫底数,
N叫真数.即
定义:
指数
真数
底数
对数
幂
底数
指数式
对数式
解:
1. 我们通常将以10为底的对数叫做常用对数. 为了简便,N的常用对数log10N简记作lgN.
2. 在科学技术中常常使用以无理数
e=2.71828……为底的对数,以e为底的对数叫自然对数,为了简便,N的自然对数logeN简记作lnN.
试试:分别说说lg5 、lg3.5、ln10、ln3的意义.
两种特殊的对数
(1)若a<0,则N取某些数值时,logaN不存在
因此,规定a不能小于0.
1.为什么对数logaN只有在a>0且a≠1时才有意义呢?
因此,规定a≠0.
探究一:
因此,规定a≠1
综上所述,对数符号logaN只有在a>0且a≠1时才有意义
由于正数的任何次幂都是正数,即ab>0
因此N>0.
底数a的取值范围(0, 1)∪(1, +∞);
真数N的取值范围(0, +∞).
2.负数和0有没有对数?
即 负数和0没有对数
探究一:
求log(1-x)(x+2)中的x的取值范围.
练习:
例2 求出下列各式中 x 值:
解:(1)
解:(2)
例2 求出下列各式中 x 值:
探究二:
loga1=?,logaa=?
loga1=0,logaa=1
练习:求下列各式x的值
解:
小结:
1.对数的定义(注意字母取值范围a>0,a≠1,N>0)
2.两个特殊对数(lgN,lnN)
3.两个等式: loga1=0,logaa=1
通过本节课的学习,你们有哪些收获?
4.应用指对数互化求值
思考:
作业:
1.必做题:第74页A组1,2
2.选做题:
(1)求对数式 中X的取值范围
(2)若 ,则X= 。
(3)计算: (a>0,b>0,c>0,N>0)
3.请同学们阅读课本,搜集有关对数发展材料,寻找有关换底公式材料,为下一步学习打基础。
谢谢!
思考:
解:成立。此式为对数恒等式。
练习:求值
解:
