圆的标准方程说课课件
图片预览










文档简介
(共41张PPT)
教材结构分析
《圆的方程》安排在高中数学必修二第四章第一节.圆作为常见的简单几何图形,在实际生活和生产实践中有着广泛的应用.圆的方程属于解析几何学的基础知识,是研究二次曲线的开始,对后续直线与圆的位置关系、圆锥曲线等内容的学习,无论在知识上还是方法上都有着积极的意义,所以本节内容在整个解析几何中起着承前启后的作用.
教学目标
知识与技能
1.掌握圆的标准方程;
2.会由圆的标准方程写出圆的半径和圆心坐标,能根据条件写出圆的标准方程;
3.利用圆的标准方程解决简单的实际问题.
教学目标
过程与方法
1.进一步培养学生用代数方法研究几何问题的能力;
2.加深对数形结合思想的理解以及对待定系数法的运用;
3.通过圆的方程在实际中的应用,增强学生用数学的意识.
教学目标
情感、态度与价值观
1.培养学生主动探究知识、合作交流的意识;
2.通过圆的方程在实际中的应用,体验数学与生活的联系,培养学生用数学的眼光审视现实生活问题的意识。
教学重点与难点
重点:
圆的标准方程的求法及其应用.
难点:
1.会根据不同的已知条件求圆的标准方程;
2.选择恰当的坐标系解决与圆有关的实际问题.
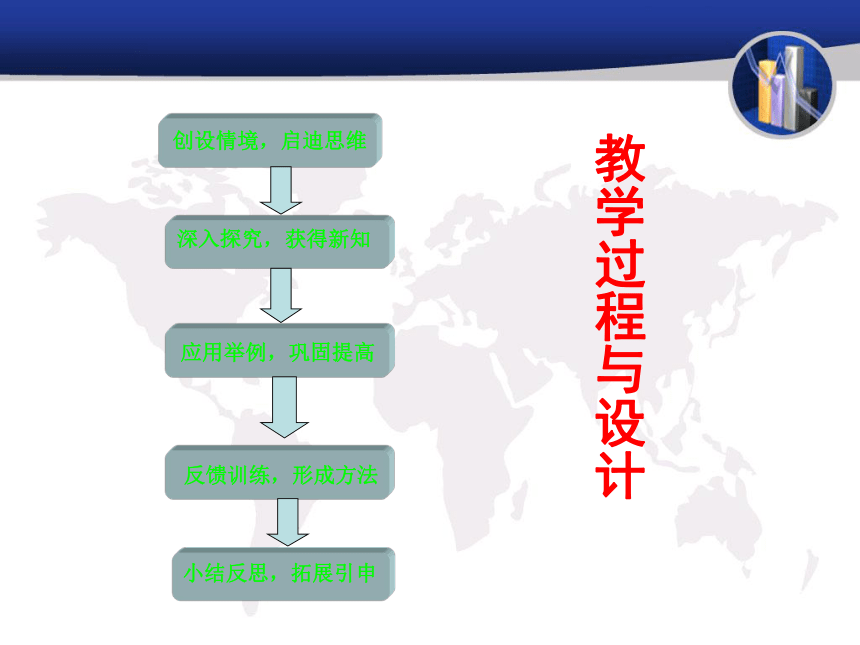
教学过程与设计
创设情境,启迪思维
深入探究,获得新知
应用举例,巩固提高
反馈训练,形成方法
小结反思,拓展引申
创设情境,启迪思维
问题一:最著名的古桥要数我国河北赵县建于1500年前的单拱石桥——赵州桥,它的设计思想和建造工艺师世界石拱桥的卓越典范,对直接后代的桥梁建筑有着十分深远的影响。它全长64.40米,最大圆拱跨径37.4米,拱高7.2米。这座桥建得科学合理精巧新奇,造型优美,通体为巨大花岗岩石块组成,很像天上的长虹,如此雄伟秀逸的圆拱形的建筑,是著名匠师李春建造的。它的建造应该说是中国古代数学、物理学、工程学融合的结晶,体现了中国古代劳动人民的智慧和力量。在赞叹之余,我们能否确定出圆拱所属圆的大小和中心呢?
什么叫做圆?
深入探究 获得新知
圆的定义:平面内与定点距离等于定长的点的集合(轨迹)是圆。
定点就是圆心,定长就是半径
哪几个要素定圆?
圆心定位
半径定形
深入探究,获得新知
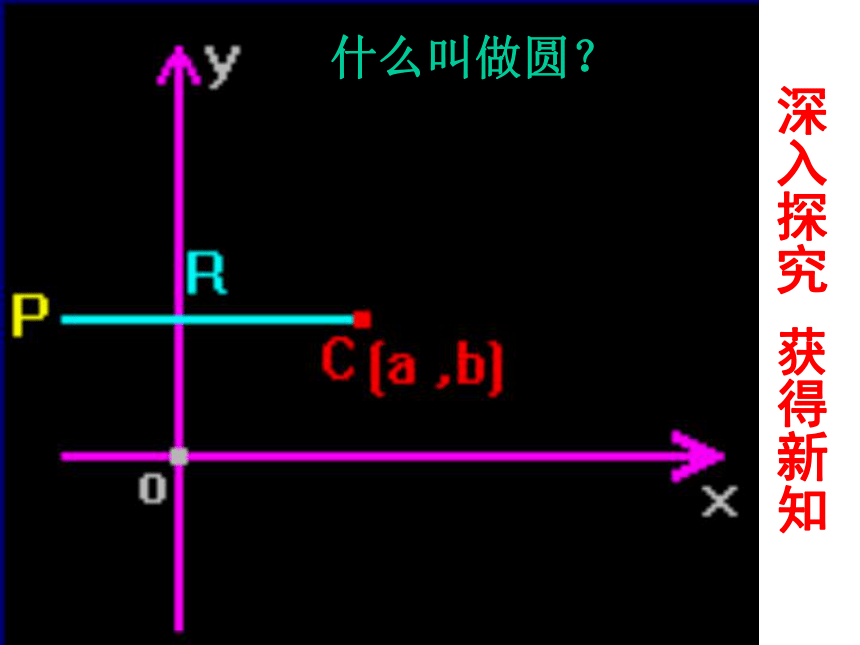
问题二 :
1.你能得到圆心在原点,半径为r的圆的方程?
2.如果圆心在C(a,b),半径为r时又如何呢?
O
A (-r,0)
P(x,y)
B (r,0)
Y
X
取圆上任意一点P(x,y),则:OP=r
即:
于是
这就是圆心在原点、半径为r的圆的方程
如果一个圆的圆心不在原点,而在点
C(ɑ,b)上,且半径为r,求此圆的方程。
X
0
根椐两点间的距离公式得:
即:
现在让我们来看看这个问题:
Y
X
0
Y
应用举例,巩固提高
直接应用 内化新知
问题三:写出圆心为 ,半径长等于5的圆的方程,并判断点 , 是否在这个圆上.
解:圆心是 ,半径长等于5的圆的标准方程是:
把 的坐标代入方程 左右两边相等,点 的坐标适合圆的方程,所以点 在这个圆上;
把点 的坐标代入此方程,左右两边不相等,点M2 的坐标不适合圆的方程,所以点M2 不在这个圆上.
怎样判断点 在圆 内呢?还是在圆外呢?
点与圆的位置关系
A
x
y
o
M1
M3
M2
从上题知道,判断一个点在不在某个圆上,只需将这个点的坐标代入这个圆的方程,如果能使圆的方程成立,则在这个圆上,反之如果不成立则不在这个圆上.
如果设点M到圆心的距离为d,则可以看到:
点在圆上 d =r ;
点在圆外 d > r ;
点在圆内 d问题四: 的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程.
待定系数法
解法一解:设所求圆的方程是 (1)
因为A(5,1), B(7,-3),C(2, -8) 都在圆上,所以它们的坐标都满足方程(1).于是
所求圆的方程为
灵活应用 提升能力
应用举例,巩固提高
确定圆的方程的方法和步骤
1.圆的标准方程中含有三个参变数,必须具备三个独立的条件;才能定出一个圆的方程,当已知曲线为圆时,一般采用待定系数法求圆的方程。
2.求圆的标准方程的一般步骤为:
(1)根据题意,设所求的圆的标准方程 为: (x-a)2+(y-b)2=r2;
(2)根据已知条件,建立关于a、b、r的方程组;
(3)解此方程组,求出a、b、r的值;
(4)将所得的a、b、r的值代回所设的圆的方程中,就得到所求的圆的标准方程.
“设”、“列”、“求”
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点
x
y
O
A(5,1)
B(7,-3)
C(2,-8)
G
问题四: 的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程.
D
E
灵活应用 提升能力
应用举例,巩固提高
问题五 : 如图是某圆拱桥的一孔圆拱的示意图,该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱的长度(精确到0.01m).
实际运用,回归自然
A
1
A
2
A
3
A
4
A
B
O
P
P
2
x
y
解:建立如图所示的坐标系,设圆心坐标是(0,b)圆的半径是r ,则圆的方程是x2+(y-b)2=r2 。
把P(0,4) B(10,0)代入圆的方程得方程组:
02+(4-b)2= r2
102+(0-b)2=r2
解得:b= -10.5 r2=14.52
所以圆的方程是: x2+(y+10.5)2=14.52
把点P2的横坐标x= -2 代入圆的方程,得
(-2)2+(y+10.5)2=14.52
因为y>0,所以y=
14.52-(-2)2 -10.5≈14.36-10.5=3.86(m)
答:支柱A2P2的长度约为3.86m。
反馈训练,形成方法
问题六 :
1.写出下列各圆的标准方程:
(1)圆心在原点,半径为3;
(2)经过点 P(5,1) ,圆心在点C(8,-3)。
2.写出下列各圆的圆心坐标和半径.
(1)(x+2)2+y2=(-2)2
(2)(x-4)2+(y+3)2=5
(3)(x+a)2+y2=a2
3.已知三角形AOB的顶点坐标分别是A(4,0),B(0,3),O(0,0),求三角形AOB的外接圆方程。
解:设所求外接圆的方程为
所求圆的方程为
P121 练习 3
圆心:直径的中点
半径:直径的一半
解:设点C(a,b)为直径
的中点,则
圆的方程为
因此点M在圆上,点N在圆外,点Q在圆内。
圆心坐标为(5,6)
小结反思,拓展引申
圆心C(a,b),半径r
x
y
O
G
A
B
C
1.圆的标准方程
2.圆心
①两条直线的交点
(弦的垂直平分线)
②直径的中点
3.会用待定系数法求圆的方程
小结反思,拓展引申
分层作业
(A)巩固型作业:教材P124:(习题4.1)1,2,3.
(B)思维拓展型作业:
试推导过圆x2+y2=r2 上一点M(xo,yo) 的切线方程
小结反思,拓展引申
激发新疑
课后练习:
1.把圆的标准方程展开后是什么形式?
2.方程 表示什么图形?
学情分析
圆的方程是学生在初中学习了圆的概念和基本性质的基础上进行研究的. 但由于学生学习解析几何的时间还不长、学习程度较浅,且对坐标法的运用还不够熟练,在学习过程中难免会出现困难.另外学生在探究问题的能力,合作交流的意识等方面有待加强.
——“启发式”问题教学法
学法分析
1.坐标法
2.三个独立条件确定圆
3.求a,b,r时可用待定系数法
教学评价
(一)突出重点 抓住关键 突破难点
(二)学生主体 教师主导 探究主线
(三)培养思维 提升能力 激励创新
直接运用
灵活运用
实际运用
a,b,r与圆的标准方程的关系
待定系数法求a,b,r
应用举例,巩固提高
问题五 : 如图是某圆拱桥的一孔圆拱的示意图,该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱的长度(精确到0.01m).
实际运用,回归自然
A
1
A
2
A
3
A
4
A
B
O
P
P
2
x
y
问题二 : 1.根据问题一的探究能不能得到圆心在原点,半径为r的圆的方程?
2.如果圆心在C(a,b),半径为r时又如何呢?
1.一般思路:坐标法
2.利用图形变换(平移)。
问题四: 的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程.
1.待定系数法;
2.通过求圆心、半径写出圆的标准方程。
由特殊到一般
归纳一般性结论
圆心在原点时,半径为r 的圆的标准方程为: x2+y2=r2 (特殊) .
圆心为C(a,b),半径为r 的圆的标准方程为:
(x-a)2+(y-b)2=r2(一般)
问题三
点与圆的位置关系
问题四
求圆的标准方程的一般步骤
附:板书设计
圆心为C(a,b),半径为r 的圆的标准方程为:
(x-a)2+(y-b)2=r2 ;
圆心在原点时,半径为r 的圆的标准方程为:x2+y2=r2 .
问题1
问题2
问题3
问题4
问题5
问题6
小结
作业
使教育过程成为一种艺术的事业——赫尔巴特
谢谢大家!
教材结构分析
《圆的方程》安排在高中数学必修二第四章第一节.圆作为常见的简单几何图形,在实际生活和生产实践中有着广泛的应用.圆的方程属于解析几何学的基础知识,是研究二次曲线的开始,对后续直线与圆的位置关系、圆锥曲线等内容的学习,无论在知识上还是方法上都有着积极的意义,所以本节内容在整个解析几何中起着承前启后的作用.
教学目标
知识与技能
1.掌握圆的标准方程;
2.会由圆的标准方程写出圆的半径和圆心坐标,能根据条件写出圆的标准方程;
3.利用圆的标准方程解决简单的实际问题.
教学目标
过程与方法
1.进一步培养学生用代数方法研究几何问题的能力;
2.加深对数形结合思想的理解以及对待定系数法的运用;
3.通过圆的方程在实际中的应用,增强学生用数学的意识.
教学目标
情感、态度与价值观
1.培养学生主动探究知识、合作交流的意识;
2.通过圆的方程在实际中的应用,体验数学与生活的联系,培养学生用数学的眼光审视现实生活问题的意识。
教学重点与难点
重点:
圆的标准方程的求法及其应用.
难点:
1.会根据不同的已知条件求圆的标准方程;
2.选择恰当的坐标系解决与圆有关的实际问题.
教学过程与设计
创设情境,启迪思维
深入探究,获得新知
应用举例,巩固提高
反馈训练,形成方法
小结反思,拓展引申
创设情境,启迪思维
问题一:最著名的古桥要数我国河北赵县建于1500年前的单拱石桥——赵州桥,它的设计思想和建造工艺师世界石拱桥的卓越典范,对直接后代的桥梁建筑有着十分深远的影响。它全长64.40米,最大圆拱跨径37.4米,拱高7.2米。这座桥建得科学合理精巧新奇,造型优美,通体为巨大花岗岩石块组成,很像天上的长虹,如此雄伟秀逸的圆拱形的建筑,是著名匠师李春建造的。它的建造应该说是中国古代数学、物理学、工程学融合的结晶,体现了中国古代劳动人民的智慧和力量。在赞叹之余,我们能否确定出圆拱所属圆的大小和中心呢?
什么叫做圆?
深入探究 获得新知
圆的定义:平面内与定点距离等于定长的点的集合(轨迹)是圆。
定点就是圆心,定长就是半径
哪几个要素定圆?
圆心定位
半径定形
深入探究,获得新知
问题二 :
1.你能得到圆心在原点,半径为r的圆的方程?
2.如果圆心在C(a,b),半径为r时又如何呢?
O
A (-r,0)
P(x,y)
B (r,0)
Y
X
取圆上任意一点P(x,y),则:OP=r
即:
于是
这就是圆心在原点、半径为r的圆的方程
如果一个圆的圆心不在原点,而在点
C(ɑ,b)上,且半径为r,求此圆的方程。
X
0
根椐两点间的距离公式得:
即:
现在让我们来看看这个问题:
Y
X
0
Y
应用举例,巩固提高
直接应用 内化新知
问题三:写出圆心为 ,半径长等于5的圆的方程,并判断点 , 是否在这个圆上.
解:圆心是 ,半径长等于5的圆的标准方程是:
把 的坐标代入方程 左右两边相等,点 的坐标适合圆的方程,所以点 在这个圆上;
把点 的坐标代入此方程,左右两边不相等,点M2 的坐标不适合圆的方程,所以点M2 不在这个圆上.
怎样判断点 在圆 内呢?还是在圆外呢?
点与圆的位置关系
A
x
y
o
M1
M3
M2
从上题知道,判断一个点在不在某个圆上,只需将这个点的坐标代入这个圆的方程,如果能使圆的方程成立,则在这个圆上,反之如果不成立则不在这个圆上.
如果设点M到圆心的距离为d,则可以看到:
点在圆上 d =r ;
点在圆外 d > r ;
点在圆内 d
待定系数法
解法一解:设所求圆的方程是 (1)
因为A(5,1), B(7,-3),C(2, -8) 都在圆上,所以它们的坐标都满足方程(1).于是
所求圆的方程为
灵活应用 提升能力
应用举例,巩固提高
确定圆的方程的方法和步骤
1.圆的标准方程中含有三个参变数,必须具备三个独立的条件;才能定出一个圆的方程,当已知曲线为圆时,一般采用待定系数法求圆的方程。
2.求圆的标准方程的一般步骤为:
(1)根据题意,设所求的圆的标准方程 为: (x-a)2+(y-b)2=r2;
(2)根据已知条件,建立关于a、b、r的方程组;
(3)解此方程组,求出a、b、r的值;
(4)将所得的a、b、r的值代回所设的圆的方程中,就得到所求的圆的标准方程.
“设”、“列”、“求”
圆心:两条弦的中垂线的交点
半径:圆心到圆上一点
x
y
O
A(5,1)
B(7,-3)
C(2,-8)
G
问题四: 的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程.
D
E
灵活应用 提升能力
应用举例,巩固提高
问题五 : 如图是某圆拱桥的一孔圆拱的示意图,该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱的长度(精确到0.01m).
实际运用,回归自然
A
1
A
2
A
3
A
4
A
B
O
P
P
2
x
y
解:建立如图所示的坐标系,设圆心坐标是(0,b)圆的半径是r ,则圆的方程是x2+(y-b)2=r2 。
把P(0,4) B(10,0)代入圆的方程得方程组:
02+(4-b)2= r2
102+(0-b)2=r2
解得:b= -10.5 r2=14.52
所以圆的方程是: x2+(y+10.5)2=14.52
把点P2的横坐标x= -2 代入圆的方程,得
(-2)2+(y+10.5)2=14.52
因为y>0,所以y=
14.52-(-2)2 -10.5≈14.36-10.5=3.86(m)
答:支柱A2P2的长度约为3.86m。
反馈训练,形成方法
问题六 :
1.写出下列各圆的标准方程:
(1)圆心在原点,半径为3;
(2)经过点 P(5,1) ,圆心在点C(8,-3)。
2.写出下列各圆的圆心坐标和半径.
(1)(x+2)2+y2=(-2)2
(2)(x-4)2+(y+3)2=5
(3)(x+a)2+y2=a2
3.已知三角形AOB的顶点坐标分别是A(4,0),B(0,3),O(0,0),求三角形AOB的外接圆方程。
解:设所求外接圆的方程为
所求圆的方程为
P121 练习 3
圆心:直径的中点
半径:直径的一半
解:设点C(a,b)为直径
的中点,则
圆的方程为
因此点M在圆上,点N在圆外,点Q在圆内。
圆心坐标为(5,6)
小结反思,拓展引申
圆心C(a,b),半径r
x
y
O
G
A
B
C
1.圆的标准方程
2.圆心
①两条直线的交点
(弦的垂直平分线)
②直径的中点
3.会用待定系数法求圆的方程
小结反思,拓展引申
分层作业
(A)巩固型作业:教材P124:(习题4.1)1,2,3.
(B)思维拓展型作业:
试推导过圆x2+y2=r2 上一点M(xo,yo) 的切线方程
小结反思,拓展引申
激发新疑
课后练习:
1.把圆的标准方程展开后是什么形式?
2.方程 表示什么图形?
学情分析
圆的方程是学生在初中学习了圆的概念和基本性质的基础上进行研究的. 但由于学生学习解析几何的时间还不长、学习程度较浅,且对坐标法的运用还不够熟练,在学习过程中难免会出现困难.另外学生在探究问题的能力,合作交流的意识等方面有待加强.
——“启发式”问题教学法
学法分析
1.坐标法
2.三个独立条件确定圆
3.求a,b,r时可用待定系数法
教学评价
(一)突出重点 抓住关键 突破难点
(二)学生主体 教师主导 探究主线
(三)培养思维 提升能力 激励创新
直接运用
灵活运用
实际运用
a,b,r与圆的标准方程的关系
待定系数法求a,b,r
应用举例,巩固提高
问题五 : 如图是某圆拱桥的一孔圆拱的示意图,该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱的长度(精确到0.01m).
实际运用,回归自然
A
1
A
2
A
3
A
4
A
B
O
P
P
2
x
y
问题二 : 1.根据问题一的探究能不能得到圆心在原点,半径为r的圆的方程?
2.如果圆心在C(a,b),半径为r时又如何呢?
1.一般思路:坐标法
2.利用图形变换(平移)。
问题四: 的三个顶点的坐标分别A(5,1), B(7,-3),C(2, -8),求它的外接圆的方程.
1.待定系数法;
2.通过求圆心、半径写出圆的标准方程。
由特殊到一般
归纳一般性结论
圆心在原点时,半径为r 的圆的标准方程为: x2+y2=r2 (特殊) .
圆心为C(a,b),半径为r 的圆的标准方程为:
(x-a)2+(y-b)2=r2(一般)
问题三
点与圆的位置关系
问题四
求圆的标准方程的一般步骤
附:板书设计
圆心为C(a,b),半径为r 的圆的标准方程为:
(x-a)2+(y-b)2=r2 ;
圆心在原点时,半径为r 的圆的标准方程为:x2+y2=r2 .
问题1
问题2
问题3
问题4
问题5
问题6
小结
作业
使教育过程成为一种艺术的事业——赫尔巴特
谢谢大家!
