第五章 §2 2.1 实际问题的函数刻画 2.2 用函数模型解决实际问题-【新教材】北师大版(2019)高中数学必修第一册练习(Word含答解析案)
文档属性
| 名称 | 第五章 §2 2.1 实际问题的函数刻画 2.2 用函数模型解决实际问题-【新教材】北师大版(2019)高中数学必修第一册练习(Word含答解析案) |

|
|
| 格式 | docx | ||
| 文件大小 | 130.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 00:00:00 | ||
图片预览




文档简介
1151890011303000第五章函数应用
§2 实际问题中的函数模型
2.1 实际问题的函数刻画
2.2 用函数模型解决实际问题
课后篇巩固提升
基础达标练
1.某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况.
加油时间
加油量/升
加油时的累计里程/千米
2019年5月1日
12
35 000
2019年5月15日
48
35 600
注:“累计里程”指汽车从出厂开始累计行驶的路程.
在这段时间内,该车每100千米平均耗油量为( )
A.6升 B.8升 C.10升 D.12升
2.某林区的森林蓄积量每年比上一年平均增长10.4%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图象大致是( )
3.(多选题)某工厂生产一种溶液,按市场要求杂质含量不得超过0.1%,而这种溶液最初的杂质含量为2%,现进行过滤,已知每过滤一次杂质含量减少13,则使产品达到市场要求的过滤次数可以为(参考数据:lg 2≈0.301,lg 3≈0.477)( )
A.6 B.9 C.8 D.7
4.已知某个病毒经30分钟可繁殖为原来的2倍,且病毒的繁殖规律为y=ekt(其中k为常数,t表示时间,单位:小时,y表示病毒个数),则k= ,经过5小时,1个病毒能繁殖 个.?
5.在一场足球比赛中,一球员从球门正前方10 m处将球踢起射向球门,当球飞行的水平距离是6 m时,球到达最高点,此时球高3 m,已知球门高2.44 m并且球按抛物线飞行, 踢进球门(填“能”或“不能”).?
6.每年的3月12日是植树节,全国各地在这一天都会开展各种形式、各种规模的义务植树活动.某市现有树木面积10万平方米,计划今后5年内扩大树木面积,有两种方案如下:
方案一:每年植树1万平方米;
方案二:每年树木面积比上年增加9%.
你觉得哪个方案较好?
7.某市电力公司在电力供不应求时期,为了让居民节约用电,采用“阶梯电价”方法计算电价,每月用电不超过100度时,按每度0.5元计费,每月用电超过100度时,超过部分按每度0.6元计费,每月用电超过150度时,超过部分按每度0.7元计费.
(1)设每月用电x度,应交电费y元,写出y关于x的函数;
(2)已知小王家第一季度缴费情况如下:
月 份
1
2
3
合 计
缴费金额
87元
62元
45元8角
194元8角
问:小王家第一季度共用了多少度电?
8.有关数据显示,中国快递行业产生的包装垃圾在2015年约为400万吨,2016年的年增长率为50%,有专家预测,如果不采取措施,未来包装垃圾还将以此增长率增长,从第几年开始,快递行业产生的包装垃圾会超过4 000万吨.(参考数据:lg 2≈0.301 0,lg 3≈0.477 1)
9.某跨国饮料公司在对全世界所有人均GDP在0.5千美元~8千美元的地区销售该公司A饮料的情况的调查中发现:人均GDP处在中等的地区对该饮料的销售量最多,然后向两边递减.
(1)下列几个模拟函数:y=ax2+bx,y=kx+b,y=logax,y=ax+b(x表示人均GDP,单位:千美元,y表示A饮料的年人均销量,单位:升),用哪个模拟函数来描述A饮料的年人均销量与地区的人均GDP关系更合适?说明理由.
(2)若人均GDP为1千美元时,A饮料的年人均销量为2升;若人均GDP为4千美元时,A饮料的年人均销量为5升,把(1)中你所选的模拟函数求出来,并求出各个地区中,A饮料的年人均销量最多是多少?
能力提升练
1.(多选题)某市出租车收费标准如下:起步价为8元,起步里程为3 km(不超过3 km按起步价付费);超过3 km但不超过8 km时,超过部分按每千米2.15元收费:超过8 km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.下列结论正确的是( )
A.出租车行驶4 km,乘客需付费9.6元
B.出租车行驶10 km,乘客需付费25.45元
C.某人乘出租车行驶5 km两次的费用超过他乘出租车行驶10 km一次的费用
D.某人乘坐一次出租车付费22.6元,则此次出租车行驶了9 km
2.某工厂生产A,B两种成本不同的产品,用于市场销售,A产品连续两次提价20%,同时B产品连续两次降价20%,结果都以每件23.04元售出,此时厂家同时出售A,B产品各一件,则盈亏情况为( )
A.亏5.20元 B.亏5.92元
C.盈6元 D.盈5元
3.已知有A,B两个水桶,桶A中开始有a L水,桶A中的水不断流入桶B,t min后,桶A中剩余的水符合指数衰减曲线y1=ae-nt,那么桶B中的水就是y2=a-ae-nt(n为常数).假设5 min时,桶A和桶B中的水量相等,再过 min,桶A中的水只有a8 L.?
4.某地区发生里氏8.0级特大地震.地震专家对发生的余震进行了监测,记录的部分数据如下表:
强度(J)
1.6×1019
3.2×1019
4.5×1019
6.4×1019
震级(里氏)
5.0
5.2
5.3
5.4
注:地震强度是指地震时释放的能量.
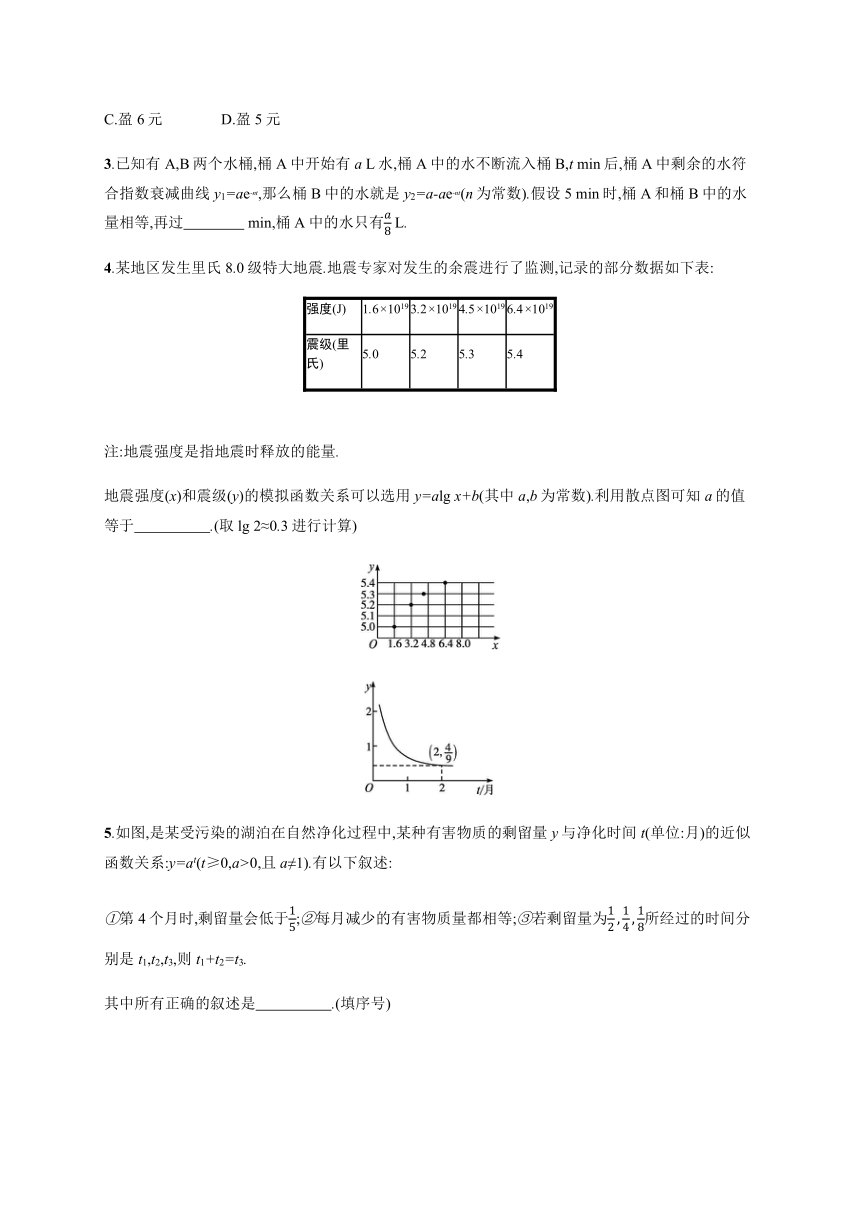
地震强度(x)和震级(y)的模拟函数关系可以选用y=alg x+b(其中a,b为常数).利用散点图可知a的值等于 .(取lg 2≈0.3进行计算)?
5.如图,是某受污染的湖泊在自然净化过程中,某种有害物质的剩留量y与净化时间t(单位:月)的近似函数关系:y=at(t≥0,a>0,且a≠1).有以下叙述:
①第4个月时,剩留量会低于15;②每月减少的有害物质量都相等;③若剩留量为12,14,18所经过的时间分别是t1,t2,t3,则t1+t2=t3.
其中所有正确的叙述是 .(填序号)?
6.某公司生产一种产品,每年投入固定成本0.5万元,此外每生产100件这种产品还需要增加投资0.25万元,经预测可知,市场对这种产品的年需求量为500件,当出售的这种产品的数量为t(单位:百件)时,销售所得的收入约为5t-12t2万元.
(1)若该公司的年产量为x(单位:百件),试把该公司生产并销售这种产品所得的年利润表示为年产量x的函数;
(2)当这种产品的年产量为多少时,当年所得利润最大?
7.科学研究表明:人类对声音有不一样的感觉,这与声音的强度I(单位:瓦/平方米)有关.在实际测量时,常用L(单位:分贝)来表示声音强弱的等级,它与声音的强度I满足关系式:L=a·lg II0(a是常数),其中I0=1×10-12瓦/平方米.如风吹落叶沙沙声的强度I=1×10-11瓦/平方米,它的强弱等级L=10分贝.
(1)已知生活中几种声音的强度如下表:
风吹落叶
沙沙声
轻声耳语
很嘈杂
的马路
强度I(瓦/
平方米)
1×10-11
1×10-10
1×10-3
强弱等级L
(分贝)
10
m
90
求a和m的值;
(2)为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
素养培优练
为减轻手术给病人带来的痛苦,麻醉师要给病人注射一定量的麻醉剂,某医院决定在某小型手术中为病人采用一种新型的麻醉剂,已知这种麻醉剂释放过程中血液中的含量y(毫克)与时间t(小时)成正比,麻醉剂释放完毕后,y与t的函数解析式为y=18t-a(a为常数),如图所示.
(1)试求从麻醉剂释放开始,血液中的麻醉剂含量y(毫克)与时间t(小时)之间的解析式;
(2)根据麻醉师的统计,当人体内血液中每升的麻醉剂含量降低到0.125毫克以下时,病人才能清醒过来,那么实施麻醉开始,至少需要经过多长时间,病人才能清醒过来?
1151890011303000第五章函数应用
§2 实际问题中的函数模型
2.1 实际问题的函数刻画
2.2 用函数模型解决实际问题
课后篇巩固提升
基础达标练
1.某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况.
加油时间
加油量/升
加油时的累计里程/千米
2019年5月1日
12
35 000
2019年5月15日
48
35 600
注:“累计里程”指汽车从出厂开始累计行驶的路程.
在这段时间内,该车每100千米平均耗油量为( )
A.6升 B.8升 C.10升 D.12升
解析因为第一次(即5月1日)把油加满,而第二次把油加满加了48升,35 600-35 000=600(千米),即汽车行驶600千米耗油48升,所以每100千米平均耗油量为8升.
答案B
2.某林区的森林蓄积量每年比上一年平均增长10.4%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图象大致是( )
解析设该林区的森林原有蓄积量为a,由题意知ax=a(1+0.104)y,即y=log1.104x(x≥1),所以y=f(x)的图象大致为D中图象.
答案D
3.(多选题)某工厂生产一种溶液,按市场要求杂质含量不得超过0.1%,而这种溶液最初的杂质含量为2%,现进行过滤,已知每过滤一次杂质含量减少13,则使产品达到市场要求的过滤次数可以为(参考数据:lg 2≈0.301,lg 3≈0.477)( )
A.6 B.9 C.8 D.7
解析设经过n次过滤,产品达到市场要求,则2100×23n≤11 000,即23n≤120,由nlg 23≤-lg 20,即n(lg 2-lg 3)≤-(1+lg 2),得n≥1+lg2lg3-lg2≈7.4.
答案BC
4.已知某个病毒经30分钟可繁殖为原来的2倍,且病毒的繁殖规律为y=ekt(其中k为常数,t表示时间,单位:小时,y表示病毒个数),则k= ,经过5小时,1个病毒能繁殖 个.?
解析当t=0.5时,y=2,∴2=e12k,∴k=2ln 2,
∴y=e2tln 2.当t=5时,y=e10ln 2=210=1 024.
答案2ln 2 1 024
5.在一场足球比赛中,一球员从球门正前方10 m处将球踢起射向球门,当球飞行的水平距离是6 m时,球到达最高点,此时球高3 m,已知球门高2.44 m并且球按抛物线飞行, 踢进球门(填“能”或“不能”).?
解析
建立如图所示的坐标系,拋物线经过点(0,0),顶点为(6,3).
设其解析式为y=a(x-6)2+3,把x=0,y=0代入,得a=-112,
∴y=-112(x-6)2+3.
当x=10时,y=-112(10-6)2+3=53<2.44.
∴球能射进球门.
答案能
6.每年的3月12日是植树节,全国各地在这一天都会开展各种形式、各种规模的义务植树活动.某市现有树木面积10万平方米,计划今后5年内扩大树木面积,有两种方案如下:
方案一:每年植树1万平方米;
方案二:每年树木面积比上年增加9%.
你觉得哪个方案较好?
解(方案一)5年后树木面积是10+1×5=15(万平方米).
(方案二)5年后树木面积是10(1+9%)5≈15.386(万平方米).∵15.386>15,∴方案二较好.
7.某市电力公司在电力供不应求时期,为了让居民节约用电,采用“阶梯电价”方法计算电价,每月用电不超过100度时,按每度0.5元计费,每月用电超过100度时,超过部分按每度0.6元计费,每月用电超过150度时,超过部分按每度0.7元计费.
(1)设每月用电x度,应交电费y元,写出y关于x的函数;
(2)已知小王家第一季度缴费情况如下:
月 份
1
2
3
合 计
缴费金额
87元
62元
45元8角
194元8角
问:小王家第一季度共用了多少度电?
解(1)依题意,当0≤x≤100时,y=0.5x,当100150时,y=0.5×100+0.6×50+0.7(x-150)=0.7x-25,所以y关于x的函数为y=0.5x,0≤x≤100,0.6x-10,100150.
(2)小王家一月份缴费87元>80元,令0.7x-25=87,得x=160,二月份缴费62元>50元,且62元<80元,
令0.6x-10=62,得x=120,
三月份缴费45.8元<50元,令0.5x=45.8,得x=91.6,
以上三个月相加得160+120+91.6=371.6(度),
所以小王家第一季度共用了371.6度电.
8.有关数据显示,中国快递行业产生的包装垃圾在2015年约为400万吨,2016年的年增长率为50%,有专家预测,如果不采取措施,未来包装垃圾还将以此增长率增长,从第几年开始,快递行业产生的包装垃圾会超过4 000万吨.(参考数据:lg 2≈0.301 0,lg 3≈0.477 1)
解设快递行业产生的包装垃圾为y万吨,n表示从2015年开始增加的年份的数量,
由题意可得y=400×(1+50%)n=400×32n,
当y=4 000时,有32n=10,两边取对数可得n(lg 3-lg 2)=1,∴n(0.477 1-0.301 0)=1,0.176 1n=1,解得n≈6,
∴从2015+6=2021年开始,快递行业产生的包装垃圾会超过4 000万吨.
9.某跨国饮料公司在对全世界所有人均GDP在0.5千美元~8千美元的地区销售该公司A饮料的情况的调查中发现:人均GDP处在中等的地区对该饮料的销售量最多,然后向两边递减.
(1)下列几个模拟函数:y=ax2+bx,y=kx+b,y=logax,y=ax+b(x表示人均GDP,单位:千美元,y表示A饮料的年人均销量,单位:升),用哪个模拟函数来描述A饮料的年人均销量与地区的人均GDP关系更合适?说明理由.
(2)若人均GDP为1千美元时,A饮料的年人均销量为2升;若人均GDP为4千美元时,A饮料的年人均销量为5升,把(1)中你所选的模拟函数求出来,并求出各个地区中,A饮料的年人均销量最多是多少?
解(1)用函数y=ax2+bx来描述A饮料的年人均销量与地区的人均GDP的关系更合适.因为函数y=kx+b,y=logax,y=ax+b在其定义域内都是单调函数,不具备先递增后递减的特征.
(2)依题意知函数过点(1,2)和(4,5),
则有a+b=2,16a+4b=5,解得a=-14,b=94,
所以y=-14x2+94x(0.5≤x≤8).
因为y=-14x2+94x=-14x-922+8116≤8116,
所以在各地区中,当x=92时,A饮料的年人均销量最多是8116升.
能力提升练
1.(多选题)某市出租车收费标准如下:起步价为8元,起步里程为3 km(不超过3 km按起步价付费);超过3 km但不超过8 km时,超过部分按每千米2.15元收费:超过8 km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.下列结论正确的是( )
A.出租车行驶4 km,乘客需付费9.6元
B.出租车行驶10 km,乘客需付费25.45元
C.某人乘出租车行驶5 km两次的费用超过他乘出租车行驶10 km一次的费用
D.某人乘坐一次出租车付费22.6元,则此次出租车行驶了9 km
解析在A中,出租车行驶4 km,乘客需付费8+1×2.15+1=11.15元,A错误;在B中,出租车行驶10 km,乘客需付费8+2.15×5+2.85×(10-8)+1=25.45元,B正确;在C中,乘出租车行驶5 km,乘客需付费8+2×2.15+1=13.30元,乘坐两次需付费26.6元,26.6>25.45,C正确;在D中,设出租车行驶x km时,付费y元,由8+5×2.15+1=19.75<22.6知x>8,因此由y=8+2.15×5+2.85(x-8)+1=22.6,解得x=9,D正确.
答案BCD
2.某工厂生产A,B两种成本不同的产品,用于市场销售,A产品连续两次提价20%,同时B产品连续两次降价20%,结果都以每件23.04元售出,此时厂家同时出售A,B产品各一件,则盈亏情况为( )
A.亏5.20元 B.亏5.92元
C.盈6元 D.盈5元
解析可设A,B的成本价分别为x元、y元,则(1+20%)2×x=23.04,(1-20%)2×y=23.04,所以x=16,y=36.成本价为x+y=52(元),实际销售额为2×23.04=46.08(元),显然亏损额为52-46.08=5.92(元).故选B.
答案B
3.已知有A,B两个水桶,桶A中开始有a L水,桶A中的水不断流入桶B,t min后,桶A中剩余的水符合指数衰减曲线y1=ae-nt,那么桶B中的水就是y2=a-ae-nt(n为常数).假设5 min时,桶A和桶B中的水量相等,再过 min,桶A中的水只有a8 L.?
解析因为5 min时,桶A和桶B中的水量相等,
所以a·e-5n=a-a·e-5n,
所以e-5n=12.令a·e-nt=a8,
则e-nt=18=123=e-15n,故有t=15.
所以再过10 min,桶A中的水只有a8 L.
答案10
4.某地区发生里氏8.0级特大地震.地震专家对发生的余震进行了监测,记录的部分数据如下表:
强度(J)
1.6×1019
3.2×1019
4.5×1019
6.4×1019
震级(里氏)
5.0
5.2
5.3
5.4
注:地震强度是指地震时释放的能量.
地震强度(x)和震级(y)的模拟函数关系可以选用y=alg x+b(其中a,b为常数).利用散点图可知a的值等于 .(取lg 2≈0.3进行计算)?
解析由记录的部分数据可知x=1.6×1019时,y=5.0,x=3.2×1019时,y=5.2.
所以5.0=alg(1.6×1019)+b,5.2=alg(3.2×1019)+b,①②
②-①,得0.2=alg3.2×10191.6×1019,0.2=alg 2.
所以a=0.2lg2=0.20.3=23.
答案23
5.如图,是某受污染的湖泊在自然净化过程中,某种有害物质的剩留量y与净化时间t(单位:月)的近似函数关系:y=at(t≥0,a>0,且a≠1).有以下叙述:
①第4个月时,剩留量会低于15;②每月减少的有害物质量都相等;③若剩留量为12,14,18所经过的时间分别是t1,t2,t3,则t1+t2=t3.
其中所有正确的叙述是 .(填序号)?
解析由图象可得,当t=2时,y=49,即a2=49,
解得a=23.故y=23t.
所以当t=4时,有害物质的剩余量为y=234=1681<15,所以①正确;
第一个月的减少量为1-231=13;
第二个月的减少量为23?232=29,显然两者不同,所以②错误;
③由已知23t1=12,23t2=14,23t3=18,所以23t1+t2=23t1×23t2=12×14=18,即23t1+t2=23t3,所以t1+t2=t3,故③正确.
答案①③
6.某公司生产一种产品,每年投入固定成本0.5万元,此外每生产100件这种产品还需要增加投资0.25万元,经预测可知,市场对这种产品的年需求量为500件,当出售的这种产品的数量为t(单位:百件)时,销售所得的收入约为5t-12t2万元.
(1)若该公司的年产量为x(单位:百件),试把该公司生产并销售这种产品所得的年利润表示为年产量x的函数;
(2)当这种产品的年产量为多少时,当年所得利润最大?
解(1)当0 当x>5时,产品只能售出500件.
所以,f(x)=5x-12x2-(0.5+0.25x),05,
即f(x)=-12x2+4.75x-0.5,05.
(2)当0 所以当x=4.75时,f(x)有最大值,f(x)max=10.781 25.
当x>5时,f(x)<12-0.25×5=10.75(万元).
故当年产量为475件时,当年所得利润最大.
7.科学研究表明:人类对声音有不一样的感觉,这与声音的强度I(单位:瓦/平方米)有关.在实际测量时,常用L(单位:分贝)来表示声音强弱的等级,它与声音的强度I满足关系式:L=a·lg II0(a是常数),其中I0=1×10-12瓦/平方米.如风吹落叶沙沙声的强度I=1×10-11瓦/平方米,它的强弱等级L=10分贝.
(1)已知生活中几种声音的强度如下表:
风吹落叶
沙沙声
轻声耳语
很嘈杂
的马路
强度I(瓦/
平方米)
1×10-11
1×10-10
1×10-3
强弱等级L
(分贝)
10
m
90
求a和m的值;
(2)为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
解(1)将I0=1×10-12瓦/平方米,I=1×10-11瓦/平方米代入L=a·lg II0,
得10=alg1×10-111×10-12=alg 10=a,
即a=10,m=10lg1×10-101×10-12=10lg 100=20.
(2)由题意得L≤50,得10lg I1×10-12≤50,
得lgI1×10-12≤5,即I1×10-12≤105,即I≤105×10-12=10-7.所以此时声音强度I的最大值为10-7瓦/平方米.
素养培优练
为减轻手术给病人带来的痛苦,麻醉师要给病人注射一定量的麻醉剂,某医院决定在某小型手术中为病人采用一种新型的麻醉剂,已知这种麻醉剂释放过程中血液中的含量y(毫克)与时间t(小时)成正比,麻醉剂释放完毕后,y与t的函数解析式为y=18t-a(a为常数),如图所示.
(1)试求从麻醉剂释放开始,血液中的麻醉剂含量y(毫克)与时间t(小时)之间的解析式;
(2)根据麻醉师的统计,当人体内血液中每升的麻醉剂含量降低到0.125毫克以下时,病人才能清醒过来,那么实施麻醉开始,至少需要经过多长时间,病人才能清醒过来?
解(1)根据题中所述,由题图可知,血液中麻醉剂的含量y(毫克)是关于时间t(小时)的一个分段函数:
当0≤t≤0.1时,函数的图象是一条经过O(0,0)的线段,设其方程为y=kt(k为待定系数),
又因为A(0.1,1)是这条线段的一个端点,代入点A的坐标得k=10,所以当0≤t≤0.1时,y=10t.
当t>0.1时,函数解析式为y=18t-a,
而A(0.1,1)在这段函数图象上,代入得:1=180.1-a,所以有0.1-a=0,解得a=0.1.故当t>0.1时,y=18t-0.1.
综上,血液中麻醉剂的含量y(毫克)与时间t(小时)之间的解析式为y=10t,0≤t≤0.1,18t-0.1,t>0.1.
(2)要使手术后的病人能清醒过来,需要麻醉剂含量降低到0.125毫克以下,此时t>0.1,且y≤0.125=18.
当t>0.1时,由18t-0.1≤18,得t-0.1≥1,解得t≥1.1.
所以至少需要经过1.1小时后病人才能清醒.
§2 实际问题中的函数模型
2.1 实际问题的函数刻画
2.2 用函数模型解决实际问题
课后篇巩固提升
基础达标练
1.某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况.
加油时间
加油量/升
加油时的累计里程/千米
2019年5月1日
12
35 000
2019年5月15日
48
35 600
注:“累计里程”指汽车从出厂开始累计行驶的路程.
在这段时间内,该车每100千米平均耗油量为( )
A.6升 B.8升 C.10升 D.12升
2.某林区的森林蓄积量每年比上一年平均增长10.4%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图象大致是( )
3.(多选题)某工厂生产一种溶液,按市场要求杂质含量不得超过0.1%,而这种溶液最初的杂质含量为2%,现进行过滤,已知每过滤一次杂质含量减少13,则使产品达到市场要求的过滤次数可以为(参考数据:lg 2≈0.301,lg 3≈0.477)( )
A.6 B.9 C.8 D.7
4.已知某个病毒经30分钟可繁殖为原来的2倍,且病毒的繁殖规律为y=ekt(其中k为常数,t表示时间,单位:小时,y表示病毒个数),则k= ,经过5小时,1个病毒能繁殖 个.?
5.在一场足球比赛中,一球员从球门正前方10 m处将球踢起射向球门,当球飞行的水平距离是6 m时,球到达最高点,此时球高3 m,已知球门高2.44 m并且球按抛物线飞行, 踢进球门(填“能”或“不能”).?
6.每年的3月12日是植树节,全国各地在这一天都会开展各种形式、各种规模的义务植树活动.某市现有树木面积10万平方米,计划今后5年内扩大树木面积,有两种方案如下:
方案一:每年植树1万平方米;
方案二:每年树木面积比上年增加9%.
你觉得哪个方案较好?
7.某市电力公司在电力供不应求时期,为了让居民节约用电,采用“阶梯电价”方法计算电价,每月用电不超过100度时,按每度0.5元计费,每月用电超过100度时,超过部分按每度0.6元计费,每月用电超过150度时,超过部分按每度0.7元计费.
(1)设每月用电x度,应交电费y元,写出y关于x的函数;
(2)已知小王家第一季度缴费情况如下:
月 份
1
2
3
合 计
缴费金额
87元
62元
45元8角
194元8角
问:小王家第一季度共用了多少度电?
8.有关数据显示,中国快递行业产生的包装垃圾在2015年约为400万吨,2016年的年增长率为50%,有专家预测,如果不采取措施,未来包装垃圾还将以此增长率增长,从第几年开始,快递行业产生的包装垃圾会超过4 000万吨.(参考数据:lg 2≈0.301 0,lg 3≈0.477 1)
9.某跨国饮料公司在对全世界所有人均GDP在0.5千美元~8千美元的地区销售该公司A饮料的情况的调查中发现:人均GDP处在中等的地区对该饮料的销售量最多,然后向两边递减.
(1)下列几个模拟函数:y=ax2+bx,y=kx+b,y=logax,y=ax+b(x表示人均GDP,单位:千美元,y表示A饮料的年人均销量,单位:升),用哪个模拟函数来描述A饮料的年人均销量与地区的人均GDP关系更合适?说明理由.
(2)若人均GDP为1千美元时,A饮料的年人均销量为2升;若人均GDP为4千美元时,A饮料的年人均销量为5升,把(1)中你所选的模拟函数求出来,并求出各个地区中,A饮料的年人均销量最多是多少?
能力提升练
1.(多选题)某市出租车收费标准如下:起步价为8元,起步里程为3 km(不超过3 km按起步价付费);超过3 km但不超过8 km时,超过部分按每千米2.15元收费:超过8 km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.下列结论正确的是( )
A.出租车行驶4 km,乘客需付费9.6元
B.出租车行驶10 km,乘客需付费25.45元
C.某人乘出租车行驶5 km两次的费用超过他乘出租车行驶10 km一次的费用
D.某人乘坐一次出租车付费22.6元,则此次出租车行驶了9 km
2.某工厂生产A,B两种成本不同的产品,用于市场销售,A产品连续两次提价20%,同时B产品连续两次降价20%,结果都以每件23.04元售出,此时厂家同时出售A,B产品各一件,则盈亏情况为( )
A.亏5.20元 B.亏5.92元
C.盈6元 D.盈5元
3.已知有A,B两个水桶,桶A中开始有a L水,桶A中的水不断流入桶B,t min后,桶A中剩余的水符合指数衰减曲线y1=ae-nt,那么桶B中的水就是y2=a-ae-nt(n为常数).假设5 min时,桶A和桶B中的水量相等,再过 min,桶A中的水只有a8 L.?
4.某地区发生里氏8.0级特大地震.地震专家对发生的余震进行了监测,记录的部分数据如下表:
强度(J)
1.6×1019
3.2×1019
4.5×1019
6.4×1019
震级(里氏)
5.0
5.2
5.3
5.4
注:地震强度是指地震时释放的能量.
地震强度(x)和震级(y)的模拟函数关系可以选用y=alg x+b(其中a,b为常数).利用散点图可知a的值等于 .(取lg 2≈0.3进行计算)?
5.如图,是某受污染的湖泊在自然净化过程中,某种有害物质的剩留量y与净化时间t(单位:月)的近似函数关系:y=at(t≥0,a>0,且a≠1).有以下叙述:
①第4个月时,剩留量会低于15;②每月减少的有害物质量都相等;③若剩留量为12,14,18所经过的时间分别是t1,t2,t3,则t1+t2=t3.
其中所有正确的叙述是 .(填序号)?
6.某公司生产一种产品,每年投入固定成本0.5万元,此外每生产100件这种产品还需要增加投资0.25万元,经预测可知,市场对这种产品的年需求量为500件,当出售的这种产品的数量为t(单位:百件)时,销售所得的收入约为5t-12t2万元.
(1)若该公司的年产量为x(单位:百件),试把该公司生产并销售这种产品所得的年利润表示为年产量x的函数;
(2)当这种产品的年产量为多少时,当年所得利润最大?
7.科学研究表明:人类对声音有不一样的感觉,这与声音的强度I(单位:瓦/平方米)有关.在实际测量时,常用L(单位:分贝)来表示声音强弱的等级,它与声音的强度I满足关系式:L=a·lg II0(a是常数),其中I0=1×10-12瓦/平方米.如风吹落叶沙沙声的强度I=1×10-11瓦/平方米,它的强弱等级L=10分贝.
(1)已知生活中几种声音的强度如下表:
风吹落叶
沙沙声
轻声耳语
很嘈杂
的马路
强度I(瓦/
平方米)
1×10-11
1×10-10
1×10-3
强弱等级L
(分贝)
10
m
90
求a和m的值;
(2)为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
素养培优练
为减轻手术给病人带来的痛苦,麻醉师要给病人注射一定量的麻醉剂,某医院决定在某小型手术中为病人采用一种新型的麻醉剂,已知这种麻醉剂释放过程中血液中的含量y(毫克)与时间t(小时)成正比,麻醉剂释放完毕后,y与t的函数解析式为y=18t-a(a为常数),如图所示.
(1)试求从麻醉剂释放开始,血液中的麻醉剂含量y(毫克)与时间t(小时)之间的解析式;
(2)根据麻醉师的统计,当人体内血液中每升的麻醉剂含量降低到0.125毫克以下时,病人才能清醒过来,那么实施麻醉开始,至少需要经过多长时间,病人才能清醒过来?
1151890011303000第五章函数应用
§2 实际问题中的函数模型
2.1 实际问题的函数刻画
2.2 用函数模型解决实际问题
课后篇巩固提升
基础达标练
1.某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况.
加油时间
加油量/升
加油时的累计里程/千米
2019年5月1日
12
35 000
2019年5月15日
48
35 600
注:“累计里程”指汽车从出厂开始累计行驶的路程.
在这段时间内,该车每100千米平均耗油量为( )
A.6升 B.8升 C.10升 D.12升
解析因为第一次(即5月1日)把油加满,而第二次把油加满加了48升,35 600-35 000=600(千米),即汽车行驶600千米耗油48升,所以每100千米平均耗油量为8升.
答案B
2.某林区的森林蓄积量每年比上一年平均增长10.4%,要增长到原来的x倍,需经过y年,则函数y=f(x)的图象大致是( )
解析设该林区的森林原有蓄积量为a,由题意知ax=a(1+0.104)y,即y=log1.104x(x≥1),所以y=f(x)的图象大致为D中图象.
答案D
3.(多选题)某工厂生产一种溶液,按市场要求杂质含量不得超过0.1%,而这种溶液最初的杂质含量为2%,现进行过滤,已知每过滤一次杂质含量减少13,则使产品达到市场要求的过滤次数可以为(参考数据:lg 2≈0.301,lg 3≈0.477)( )
A.6 B.9 C.8 D.7
解析设经过n次过滤,产品达到市场要求,则2100×23n≤11 000,即23n≤120,由nlg 23≤-lg 20,即n(lg 2-lg 3)≤-(1+lg 2),得n≥1+lg2lg3-lg2≈7.4.
答案BC
4.已知某个病毒经30分钟可繁殖为原来的2倍,且病毒的繁殖规律为y=ekt(其中k为常数,t表示时间,单位:小时,y表示病毒个数),则k= ,经过5小时,1个病毒能繁殖 个.?
解析当t=0.5时,y=2,∴2=e12k,∴k=2ln 2,
∴y=e2tln 2.当t=5时,y=e10ln 2=210=1 024.
答案2ln 2 1 024
5.在一场足球比赛中,一球员从球门正前方10 m处将球踢起射向球门,当球飞行的水平距离是6 m时,球到达最高点,此时球高3 m,已知球门高2.44 m并且球按抛物线飞行, 踢进球门(填“能”或“不能”).?
解析
建立如图所示的坐标系,拋物线经过点(0,0),顶点为(6,3).
设其解析式为y=a(x-6)2+3,把x=0,y=0代入,得a=-112,
∴y=-112(x-6)2+3.
当x=10时,y=-112(10-6)2+3=53<2.44.
∴球能射进球门.
答案能
6.每年的3月12日是植树节,全国各地在这一天都会开展各种形式、各种规模的义务植树活动.某市现有树木面积10万平方米,计划今后5年内扩大树木面积,有两种方案如下:
方案一:每年植树1万平方米;
方案二:每年树木面积比上年增加9%.
你觉得哪个方案较好?
解(方案一)5年后树木面积是10+1×5=15(万平方米).
(方案二)5年后树木面积是10(1+9%)5≈15.386(万平方米).∵15.386>15,∴方案二较好.
7.某市电力公司在电力供不应求时期,为了让居民节约用电,采用“阶梯电价”方法计算电价,每月用电不超过100度时,按每度0.5元计费,每月用电超过100度时,超过部分按每度0.6元计费,每月用电超过150度时,超过部分按每度0.7元计费.
(1)设每月用电x度,应交电费y元,写出y关于x的函数;
(2)已知小王家第一季度缴费情况如下:
月 份
1
2
3
合 计
缴费金额
87元
62元
45元8角
194元8角
问:小王家第一季度共用了多少度电?
解(1)依题意,当0≤x≤100时,y=0.5x,当100
(2)小王家一月份缴费87元>80元,令0.7x-25=87,得x=160,二月份缴费62元>50元,且62元<80元,
令0.6x-10=62,得x=120,
三月份缴费45.8元<50元,令0.5x=45.8,得x=91.6,
以上三个月相加得160+120+91.6=371.6(度),
所以小王家第一季度共用了371.6度电.
8.有关数据显示,中国快递行业产生的包装垃圾在2015年约为400万吨,2016年的年增长率为50%,有专家预测,如果不采取措施,未来包装垃圾还将以此增长率增长,从第几年开始,快递行业产生的包装垃圾会超过4 000万吨.(参考数据:lg 2≈0.301 0,lg 3≈0.477 1)
解设快递行业产生的包装垃圾为y万吨,n表示从2015年开始增加的年份的数量,
由题意可得y=400×(1+50%)n=400×32n,
当y=4 000时,有32n=10,两边取对数可得n(lg 3-lg 2)=1,∴n(0.477 1-0.301 0)=1,0.176 1n=1,解得n≈6,
∴从2015+6=2021年开始,快递行业产生的包装垃圾会超过4 000万吨.
9.某跨国饮料公司在对全世界所有人均GDP在0.5千美元~8千美元的地区销售该公司A饮料的情况的调查中发现:人均GDP处在中等的地区对该饮料的销售量最多,然后向两边递减.
(1)下列几个模拟函数:y=ax2+bx,y=kx+b,y=logax,y=ax+b(x表示人均GDP,单位:千美元,y表示A饮料的年人均销量,单位:升),用哪个模拟函数来描述A饮料的年人均销量与地区的人均GDP关系更合适?说明理由.
(2)若人均GDP为1千美元时,A饮料的年人均销量为2升;若人均GDP为4千美元时,A饮料的年人均销量为5升,把(1)中你所选的模拟函数求出来,并求出各个地区中,A饮料的年人均销量最多是多少?
解(1)用函数y=ax2+bx来描述A饮料的年人均销量与地区的人均GDP的关系更合适.因为函数y=kx+b,y=logax,y=ax+b在其定义域内都是单调函数,不具备先递增后递减的特征.
(2)依题意知函数过点(1,2)和(4,5),
则有a+b=2,16a+4b=5,解得a=-14,b=94,
所以y=-14x2+94x(0.5≤x≤8).
因为y=-14x2+94x=-14x-922+8116≤8116,
所以在各地区中,当x=92时,A饮料的年人均销量最多是8116升.
能力提升练
1.(多选题)某市出租车收费标准如下:起步价为8元,起步里程为3 km(不超过3 km按起步价付费);超过3 km但不超过8 km时,超过部分按每千米2.15元收费:超过8 km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.下列结论正确的是( )
A.出租车行驶4 km,乘客需付费9.6元
B.出租车行驶10 km,乘客需付费25.45元
C.某人乘出租车行驶5 km两次的费用超过他乘出租车行驶10 km一次的费用
D.某人乘坐一次出租车付费22.6元,则此次出租车行驶了9 km
解析在A中,出租车行驶4 km,乘客需付费8+1×2.15+1=11.15元,A错误;在B中,出租车行驶10 km,乘客需付费8+2.15×5+2.85×(10-8)+1=25.45元,B正确;在C中,乘出租车行驶5 km,乘客需付费8+2×2.15+1=13.30元,乘坐两次需付费26.6元,26.6>25.45,C正确;在D中,设出租车行驶x km时,付费y元,由8+5×2.15+1=19.75<22.6知x>8,因此由y=8+2.15×5+2.85(x-8)+1=22.6,解得x=9,D正确.
答案BCD
2.某工厂生产A,B两种成本不同的产品,用于市场销售,A产品连续两次提价20%,同时B产品连续两次降价20%,结果都以每件23.04元售出,此时厂家同时出售A,B产品各一件,则盈亏情况为( )
A.亏5.20元 B.亏5.92元
C.盈6元 D.盈5元
解析可设A,B的成本价分别为x元、y元,则(1+20%)2×x=23.04,(1-20%)2×y=23.04,所以x=16,y=36.成本价为x+y=52(元),实际销售额为2×23.04=46.08(元),显然亏损额为52-46.08=5.92(元).故选B.
答案B
3.已知有A,B两个水桶,桶A中开始有a L水,桶A中的水不断流入桶B,t min后,桶A中剩余的水符合指数衰减曲线y1=ae-nt,那么桶B中的水就是y2=a-ae-nt(n为常数).假设5 min时,桶A和桶B中的水量相等,再过 min,桶A中的水只有a8 L.?
解析因为5 min时,桶A和桶B中的水量相等,
所以a·e-5n=a-a·e-5n,
所以e-5n=12.令a·e-nt=a8,
则e-nt=18=123=e-15n,故有t=15.
所以再过10 min,桶A中的水只有a8 L.
答案10
4.某地区发生里氏8.0级特大地震.地震专家对发生的余震进行了监测,记录的部分数据如下表:
强度(J)
1.6×1019
3.2×1019
4.5×1019
6.4×1019
震级(里氏)
5.0
5.2
5.3
5.4
注:地震强度是指地震时释放的能量.
地震强度(x)和震级(y)的模拟函数关系可以选用y=alg x+b(其中a,b为常数).利用散点图可知a的值等于 .(取lg 2≈0.3进行计算)?
解析由记录的部分数据可知x=1.6×1019时,y=5.0,x=3.2×1019时,y=5.2.
所以5.0=alg(1.6×1019)+b,5.2=alg(3.2×1019)+b,①②
②-①,得0.2=alg3.2×10191.6×1019,0.2=alg 2.
所以a=0.2lg2=0.20.3=23.
答案23
5.如图,是某受污染的湖泊在自然净化过程中,某种有害物质的剩留量y与净化时间t(单位:月)的近似函数关系:y=at(t≥0,a>0,且a≠1).有以下叙述:
①第4个月时,剩留量会低于15;②每月减少的有害物质量都相等;③若剩留量为12,14,18所经过的时间分别是t1,t2,t3,则t1+t2=t3.
其中所有正确的叙述是 .(填序号)?
解析由图象可得,当t=2时,y=49,即a2=49,
解得a=23.故y=23t.
所以当t=4时,有害物质的剩余量为y=234=1681<15,所以①正确;
第一个月的减少量为1-231=13;
第二个月的减少量为23?232=29,显然两者不同,所以②错误;
③由已知23t1=12,23t2=14,23t3=18,所以23t1+t2=23t1×23t2=12×14=18,即23t1+t2=23t3,所以t1+t2=t3,故③正确.
答案①③
6.某公司生产一种产品,每年投入固定成本0.5万元,此外每生产100件这种产品还需要增加投资0.25万元,经预测可知,市场对这种产品的年需求量为500件,当出售的这种产品的数量为t(单位:百件)时,销售所得的收入约为5t-12t2万元.
(1)若该公司的年产量为x(单位:百件),试把该公司生产并销售这种产品所得的年利润表示为年产量x的函数;
(2)当这种产品的年产量为多少时,当年所得利润最大?
解(1)当0
所以,f(x)=5x-12x2-(0.5+0.25x),0
即f(x)=-12x2+4.75x-0.5,0
(2)当0
当x>5时,f(x)<12-0.25×5=10.75(万元).
故当年产量为475件时,当年所得利润最大.
7.科学研究表明:人类对声音有不一样的感觉,这与声音的强度I(单位:瓦/平方米)有关.在实际测量时,常用L(单位:分贝)来表示声音强弱的等级,它与声音的强度I满足关系式:L=a·lg II0(a是常数),其中I0=1×10-12瓦/平方米.如风吹落叶沙沙声的强度I=1×10-11瓦/平方米,它的强弱等级L=10分贝.
(1)已知生活中几种声音的强度如下表:
风吹落叶
沙沙声
轻声耳语
很嘈杂
的马路
强度I(瓦/
平方米)
1×10-11
1×10-10
1×10-3
强弱等级L
(分贝)
10
m
90
求a和m的值;
(2)为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
解(1)将I0=1×10-12瓦/平方米,I=1×10-11瓦/平方米代入L=a·lg II0,
得10=alg1×10-111×10-12=alg 10=a,
即a=10,m=10lg1×10-101×10-12=10lg 100=20.
(2)由题意得L≤50,得10lg I1×10-12≤50,
得lgI1×10-12≤5,即I1×10-12≤105,即I≤105×10-12=10-7.所以此时声音强度I的最大值为10-7瓦/平方米.
素养培优练
为减轻手术给病人带来的痛苦,麻醉师要给病人注射一定量的麻醉剂,某医院决定在某小型手术中为病人采用一种新型的麻醉剂,已知这种麻醉剂释放过程中血液中的含量y(毫克)与时间t(小时)成正比,麻醉剂释放完毕后,y与t的函数解析式为y=18t-a(a为常数),如图所示.
(1)试求从麻醉剂释放开始,血液中的麻醉剂含量y(毫克)与时间t(小时)之间的解析式;
(2)根据麻醉师的统计,当人体内血液中每升的麻醉剂含量降低到0.125毫克以下时,病人才能清醒过来,那么实施麻醉开始,至少需要经过多长时间,病人才能清醒过来?
解(1)根据题中所述,由题图可知,血液中麻醉剂的含量y(毫克)是关于时间t(小时)的一个分段函数:
当0≤t≤0.1时,函数的图象是一条经过O(0,0)的线段,设其方程为y=kt(k为待定系数),
又因为A(0.1,1)是这条线段的一个端点,代入点A的坐标得k=10,所以当0≤t≤0.1时,y=10t.
当t>0.1时,函数解析式为y=18t-a,
而A(0.1,1)在这段函数图象上,代入得:1=180.1-a,所以有0.1-a=0,解得a=0.1.故当t>0.1时,y=18t-0.1.
综上,血液中麻醉剂的含量y(毫克)与时间t(小时)之间的解析式为y=10t,0≤t≤0.1,18t-0.1,t>0.1.
(2)要使手术后的病人能清醒过来,需要麻醉剂含量降低到0.125毫克以下,此时t>0.1,且y≤0.125=18.
当t>0.1时,由18t-0.1≤18,得t-0.1≥1,解得t≥1.1.
所以至少需要经过1.1小时后病人才能清醒.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
