五年级下册数学教案-6.5 图形与几何-周长、面积、表面积和体积复习教案 沪教版
文档属性
| 名称 | 五年级下册数学教案-6.5 图形与几何-周长、面积、表面积和体积复习教案 沪教版 |

|
|
| 格式 | doc | ||
| 文件大小 | 106.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 00:00:00 | ||
图片预览


文档简介
周长、面积、表面积和体积
知识与技能:
1、通过复习整理各种几何图形的周长、面积、表面积及体积公式,使学生将空间的知识形成网状结构体系。
2、熟练地掌握长度单位、面积单位及体积
单位之间的换算。
3、在复习中能巩固平面图形与立体图形的有关计算公式并能灵活应用。
过程与方法:
1、进一步培养学生的空间观念以及对知识进行分析、比较、归纳、整理的学习能力。
2、灵活运用平面图形的周长面积计算方法和立体图形的表面积体积的计算方法解决实际问题。
情感与态度:
让学生在解决实际问题的过程中,感受数学与生活的联系,体会数学的价值,进一步培养学生的合作意识和创新精神。
教学过程:
我们学过一些基本图形的周长、面积、表面积及体积公式。下面我们就先来整理复习一下这些图形的周长、面积公式。
探究一:
1、填写书本P98
平面图形计算公式
2、整理周长、面积的意义与单位:
周长
意义:图形一周长的长度等于图形所有边的和
单位:米
10
分米
10
厘米
10
毫米
面积
意义:平面图形的大小
单位:平方千米
1000000
平方米
平方米
100
平方分米
100平方厘米
3、练习:
(1)教室里有1块长35dm,宽8dm的黑板,若给它四周嵌上一条铝合金,则需要铝合金多长?要给它重新涂上一层黑漆,需要涂漆多少平方分米?
(35+8)×2
35×8=280(dm2)
=43×2
=86(dm)
答:需要铝合金86dm。需要涂漆280
dm2。
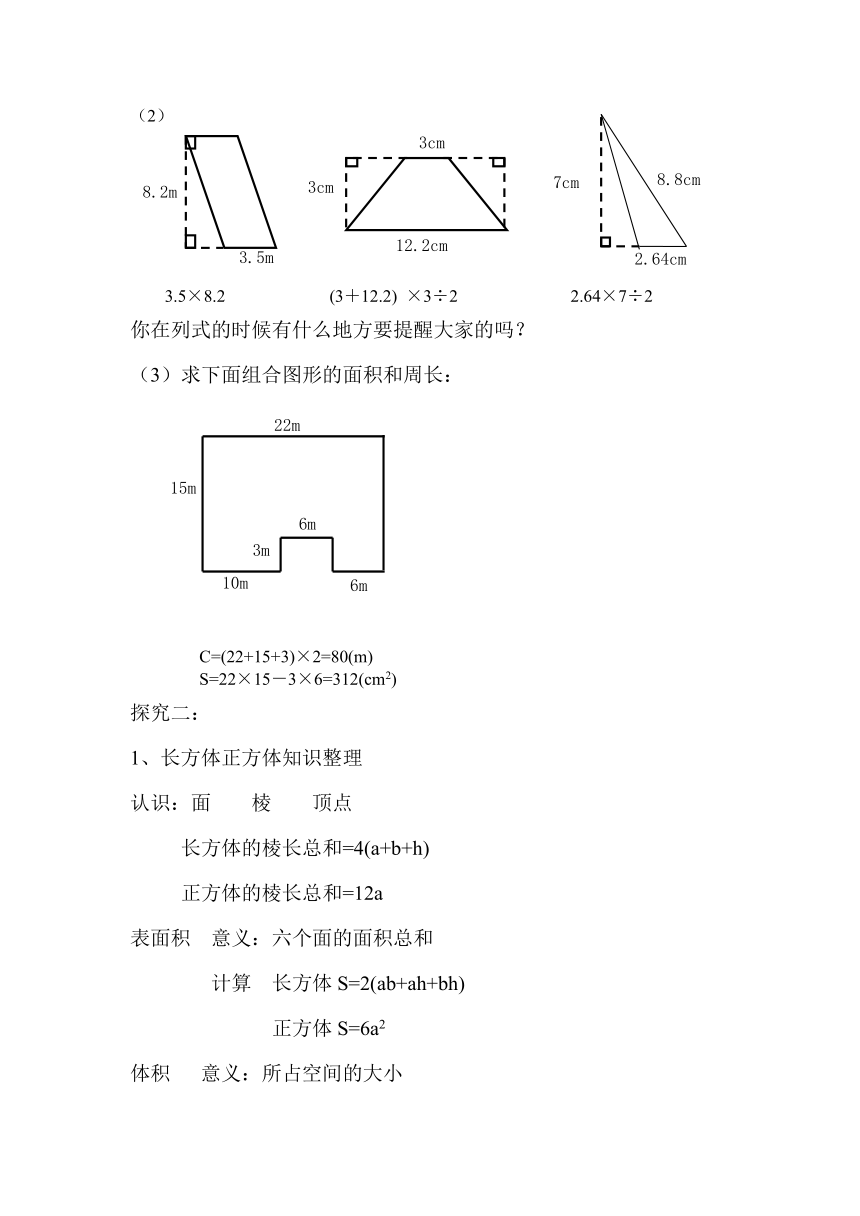
(2)口答:求下面图形的面积
(2)
3.5×8.2
(3+12.2)
×3÷2
2.64×7÷2
你在列式的时候有什么地方要提醒大家的吗?
(3)求下面组合图形的面积和周长:
C=(22+15+3)×2=80(m)
S=22×15-3×6=312(cm2)
探究二:
1、长方体正方体知识整理
认识:面
棱
顶点
长方体的棱长总和=4(a+b+h)
正方体的棱长总和=12a
表面积
意义:六个面的面积总和
计算
长方体S=2(ab+ah+bh)
正方体S=6a2
体积
意义:所占空间的大小
计算:长方体V=abh
正方体V=a3
单位:立方米
1000
立方分米
1000
立方厘米
容积
意义:所容纳物体的体积
单位:升
1000
毫升
测量方法:有(无)壁厚
2、把书本立体图形公式填完整
3、练习:
(1)求下列正方体、长方体的体积和表面积:
要求:只列式不计算
V=7.5×5×4=150(cm3)
S=(7.5×5+7.5×4+5×4)×2
=87.5×2
=175(cm2)
V=9×9×9=27(dm3)
S=9×9×6
=486(dm2)
(2)下面三个算式都是求右图所示图形体积的算式,它们分别是怎样考虑的?从下面a—c是选出对应的图。
(1)
8×4×7+8×6×(7-3)
b
(2)
8×7×(6+4)-8×6×3
c
(3)
8×(6+4)
×(7-3)+8×4×3
a
(3)
a、这个鱼缸占地面积是多少?
b、做10个这样的鱼缸至少需要玻璃多少平方分米?
c、如果鱼缸里水深5分米,1升水的重量是1千克,
这些水的重量是多少千克?
区别这些题目分别求的是什么?
总结:
总板书:
周长、面积、表面积、体积复面图形
周长
意义:图形一周长的长度等于图形所有边的和
单位:米
10
分米
10
厘米
10
毫米
面积
意义:平面图形的大小
单位:平方千米
1000000
平方米
平方米
100
平方分米
100平方厘米
立体图形
认识:面
棱
顶点
长方体的棱长总和=4(a+b+h)
正方体的棱长总和=12a
表面积
意义:六个面的面积总和
计算
长方体S=2(ab+ah+bh)
正方体S=6a2
体积
意义:所占空间的大小
计算:长方体V=abh
正方体V=a3
单位:立方米
1000
立方分米
1000
立方厘米
容积
意义:所容纳物体的体积
单位:升
1000
毫升
测量方法:有壁厚时:从容器里面测量长、宽、高
知识与技能:
1、通过复习整理各种几何图形的周长、面积、表面积及体积公式,使学生将空间的知识形成网状结构体系。
2、熟练地掌握长度单位、面积单位及体积
单位之间的换算。
3、在复习中能巩固平面图形与立体图形的有关计算公式并能灵活应用。
过程与方法:
1、进一步培养学生的空间观念以及对知识进行分析、比较、归纳、整理的学习能力。
2、灵活运用平面图形的周长面积计算方法和立体图形的表面积体积的计算方法解决实际问题。
情感与态度:
让学生在解决实际问题的过程中,感受数学与生活的联系,体会数学的价值,进一步培养学生的合作意识和创新精神。
教学过程:
我们学过一些基本图形的周长、面积、表面积及体积公式。下面我们就先来整理复习一下这些图形的周长、面积公式。
探究一:
1、填写书本P98
平面图形计算公式
2、整理周长、面积的意义与单位:
周长
意义:图形一周长的长度等于图形所有边的和
单位:米
10
分米
10
厘米
10
毫米
面积
意义:平面图形的大小
单位:平方千米
1000000
平方米
平方米
100
平方分米
100平方厘米
3、练习:
(1)教室里有1块长35dm,宽8dm的黑板,若给它四周嵌上一条铝合金,则需要铝合金多长?要给它重新涂上一层黑漆,需要涂漆多少平方分米?
(35+8)×2
35×8=280(dm2)
=43×2
=86(dm)
答:需要铝合金86dm。需要涂漆280
dm2。
(2)口答:求下面图形的面积
(2)
3.5×8.2
(3+12.2)
×3÷2
2.64×7÷2
你在列式的时候有什么地方要提醒大家的吗?
(3)求下面组合图形的面积和周长:
C=(22+15+3)×2=80(m)
S=22×15-3×6=312(cm2)
探究二:
1、长方体正方体知识整理
认识:面
棱
顶点
长方体的棱长总和=4(a+b+h)
正方体的棱长总和=12a
表面积
意义:六个面的面积总和
计算
长方体S=2(ab+ah+bh)
正方体S=6a2
体积
意义:所占空间的大小
计算:长方体V=abh
正方体V=a3
单位:立方米
1000
立方分米
1000
立方厘米
容积
意义:所容纳物体的体积
单位:升
1000
毫升
测量方法:有(无)壁厚
2、把书本立体图形公式填完整
3、练习:
(1)求下列正方体、长方体的体积和表面积:
要求:只列式不计算
V=7.5×5×4=150(cm3)
S=(7.5×5+7.5×4+5×4)×2
=87.5×2
=175(cm2)
V=9×9×9=27(dm3)
S=9×9×6
=486(dm2)
(2)下面三个算式都是求右图所示图形体积的算式,它们分别是怎样考虑的?从下面a—c是选出对应的图。
(1)
8×4×7+8×6×(7-3)
b
(2)
8×7×(6+4)-8×6×3
c
(3)
8×(6+4)
×(7-3)+8×4×3
a
(3)
a、这个鱼缸占地面积是多少?
b、做10个这样的鱼缸至少需要玻璃多少平方分米?
c、如果鱼缸里水深5分米,1升水的重量是1千克,
这些水的重量是多少千克?
区别这些题目分别求的是什么?
总结:
总板书:
周长、面积、表面积、体积复面图形
周长
意义:图形一周长的长度等于图形所有边的和
单位:米
10
分米
10
厘米
10
毫米
面积
意义:平面图形的大小
单位:平方千米
1000000
平方米
平方米
100
平方分米
100平方厘米
立体图形
认识:面
棱
顶点
长方体的棱长总和=4(a+b+h)
正方体的棱长总和=12a
表面积
意义:六个面的面积总和
计算
长方体S=2(ab+ah+bh)
正方体S=6a2
体积
意义:所占空间的大小
计算:长方体V=abh
正方体V=a3
单位:立方米
1000
立方分米
1000
立方厘米
容积
意义:所容纳物体的体积
单位:升
1000
毫升
测量方法:有壁厚时:从容器里面测量长、宽、高
