2020-2021学年四川省成都市武侯区七年级(下)期末数学试卷 (word版含解析)
文档属性
| 名称 | 2020-2021学年四川省成都市武侯区七年级(下)期末数学试卷 (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 698.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-24 07:37:57 | ||
图片预览



文档简介
2020-2021学年四川省成都市武侯区七年级(下)期末数学试卷
一、选择题(共10个小题,每小题3分)
1.下列运算正确的是( )
A.x+x2=x3 B.x8÷x2=x4 C.(3x2)2=9x4 D.x3?x2=x6
2.下列各图是选自历届世界大运会的会徽图案,其中是轴对称图形的是( )
A. B. C. D.
3.2020年国产芯片迎来最好的时刻,中芯国际宣布中芯南方厂第一代14纳米FinFET工艺,即中国首条14纳米芯片生产线已成功投产,月产能为3.5万片.其中14纳米=0.000000014米,将数据0.000000014用科学记数法表示为( )
A.1.4×10﹣8 B.14×10﹣8 C.1.4×10﹣9 D.14×10﹣9
4.掷一枚质地均匀的骰子,前3次都是6点朝上,掷第4次时6点朝上的概率是( )
A.1 B. C. D.
5.如图,AB∥CD,∠CEF=61°,那么∠A的度数为( )
A.29° B.61° C.119° D.129°
6.已知x﹣y=4,xy=2,那么(x+y)2的值为( )
A.24 B.20 C.12 D.8
7.根据下列已知条件,能确定△ABC的形状和大小的是( )
A.∠A=50°,∠B=60°,∠C=70° B.∠A=50°,∠B=50°,AB=5cm
C.AB=5cm,AC=4cm,∠B=30° D.AB=6cm,BC=4cm,∠A=30°
8.若一个长方形的周长为20cm,一条边长为xcm(x>0),面积为ycm2,则y与x之间满足的关系式为( )
A.y=x2 B.y=(20﹣x)2 C.y=x?(20﹣x) D.y=x?(10﹣x)
9.从﹣6,﹣3,0,3,6五个数中任选一个数作为m的值,能使得x2﹣2mx+9是关于x的完全平方式的概率是( )
A. B. C. D.
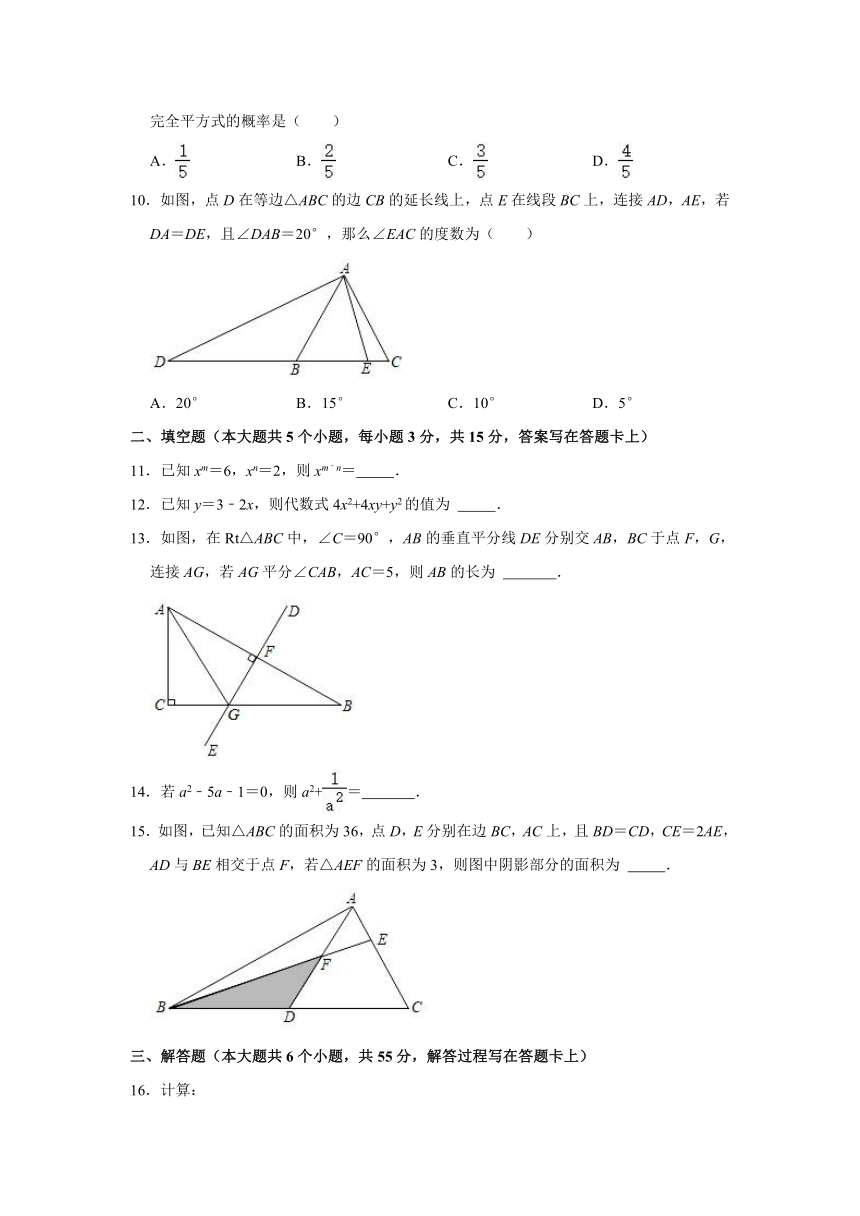
10.如图,点D在等边△ABC的边CB的延长线上,点E在线段BC上,连接AD,AE,若DA=DE,且∠DAB=20°,那么∠EAC的度数为( )
A.20° B.15° C.10° D.5°
二、填空题(本大题共5个小题,每小题3分,共15分,答案写在答题卡上)
11.已知xm=6,xn=2,则xm﹣n= .
12.已知y=3﹣2x,则代数式4x2+4xy+y2的值为 .
13.如图,在Rt△ABC中,∠C=90°,AB的垂直平分线DE分别交AB,BC于点F,G,连接AG,若AG平分∠CAB,AC=5,则AB的长为 .
14.若a2﹣5a﹣1=0,则a2+= .
15.如图,已知△ABC的面积为36,点D,E分别在边BC,AC上,且BD=CD,CE=2AE,AD与BE相交于点F,若△AEF的面积为3,则图中阴影部分的面积为 .
三、解答题(本大题共6个小题,共55分,解答过程写在答题卡上)
16.计算:
(1)(﹣2)2﹣(π﹣2021)0+9×()﹣2;
(2)(x+2)(2x﹣5)﹣x(2x﹣1).
17.(1)先化简,再求值:[(2x﹣y)2﹣(x﹣y)(x+y)﹣2y2]÷x,其中x=2,y=﹣3;
(2)已知a为常数,关于x的代数式(x2﹣3x+2)(x2+ax)的化简结果中不含x3项,且(m﹣2)2+|n﹣3|=0,求am﹣n的值
18.已知:如图,AB∥DE,AC∥DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)过点C作CG⊥AB于点G,若S△ABC=9,DE=6,求CG的长.
19.一辆客车和一辆货车沿同一条公路从甲地同时出发驶往乙地,两车均匀速行驶,客车每小时行驶80km,货车每小时行驶60km,货车在途中休息了一段时间后按原速继续匀速行驶,客车直达乙地后原地等待货车到达,两车之间的距离s(km)与货车行驶时间t(h)之间的关系如图所示,请结合图中信息解答下列问题:
(1)填空m的值为 ;
(2)试问:货车在途中休息了多长时间?
(3)求当t为何值时,两车相距60km.
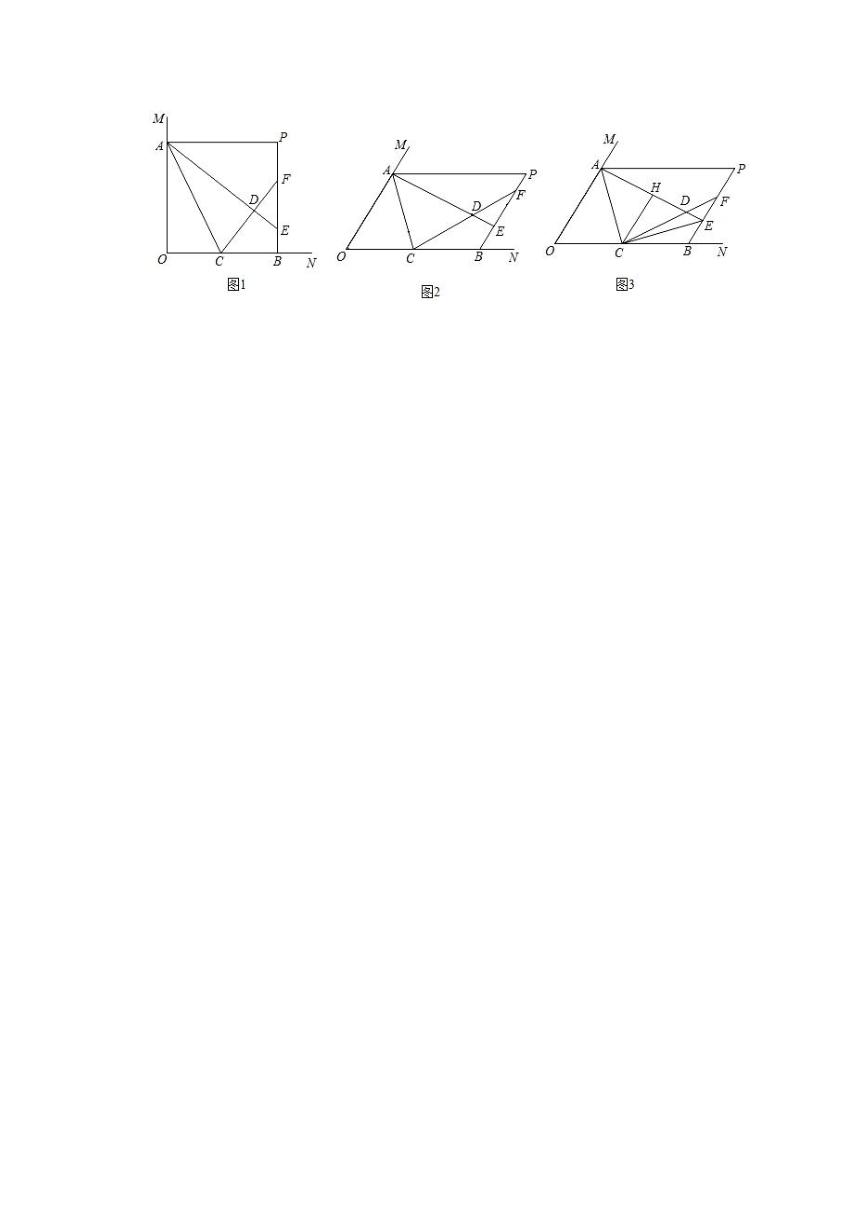
20.已知图1所示的图形是一个轴对称图形,把图1看成一个基本图形,用若干相同的基本图形进行拼图(重合处无缝隙).
(1)如图1,用含a,b的代数式表示c;
(2)如图2,将两个基本图形进行拼图,得到正方形ABCD和正方形EFGH,求阴影部分的面积(用含c的代数式表示);
(3)如图3,将四个基本图形进行拼图,连接其中四个顶点,得到正方形MNPQ,请结合图1,图2的信息直接写出阴影部分的面积(用含c的代数式表示).
21.如图,点P是∠MON内部一点,过点P分别作PA∥ON交OM于点A,PB∥OM交ON于点B(PA≥PB),在线段OB上取一点C,连接AC,将△AOC沿直线AC翻折,得到△ADC,延长AD交PB于点E,延长CD交PB于点F.
(1)如图1,当四边形AOBP是正方形时,求证:DF=PF;
(2)如图2,当C为OB中点时,试探究线段AE,AO,BE之间满足的数量关系,并说明理由;
(3)如图3,在(2)的条件下,连接CE,∠ACE的平分线CH交AE于点H,设OA=a,BE=b,若∠CAO=∠CEB,求△CDH的面积(用含a,b的代数式表示).
参考答案
一、选择题(本大题共10个小题,每小题3分共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
1.下列运算正确的是( )
A.x+x2=x3 B.x8÷x2=x4 C.(3x2)2=9x4 D.x3?x2=x6
解:A、x与x2不是同类项,不能合并计算,故此选项不符合题意;
B、x8÷x2=x6,故此选项不符合题意;
C、(3x2)2=9x4,正确,故此选项符合题意;
D、x3?x2=x5,故此选项不符合题意;
故选:C.
2.下列各图是选自历届世界大运会的会徽图案,其中是轴对称图形的是( )
A. B. C. D.
解:A.不是轴对称图形,故本选项不合题意;
B.是轴对称图形,故本选项符合题意;
C.不是轴对称图形,故本选项不合题意;
D.不是轴对称图形,故本选项不合题意.
故选:B.
3.2020年国产芯片迎来最好的时刻,中芯国际宣布中芯南方厂第一代14纳米FinFET工艺,即中国首条14纳米芯片生产线已成功投产,月产能为3.5万片.其中14纳米=0.000000014米,将数据0.000000014用科学记数法表示为( )
A.1.4×10﹣8 B.14×10﹣8 C.1.4×10﹣9 D.14×10﹣9
解:0.000000014=1.4×10﹣8.
故选:A.
4.掷一枚质地均匀的骰子,前3次都是6点朝上,掷第4次时6点朝上的概率是( )
A.1 B. C. D.
解:掷一枚质地均匀的骰子,前3次都是6点朝上,
掷第4次时,不会受前3次的影响,
掷第4次时仍有6种等可能出现的结果,其中6点朝上的有1种,
所以掷第4次时6点朝上的概率是,
故选:D.
5.如图,AB∥CD,∠CEF=61°,那么∠A的度数为( )
A.29° B.61° C.119° D.129°
解:∵AB∥CD,
∴∠A+∠AED=180°,
∵∠AED=∠CEF=61°,
∴∠A=180°﹣61°=119°,
故选:C.
6.已知x﹣y=4,xy=2,那么(x+y)2的值为( )
A.24 B.20 C.12 D.8
解:(x+y)2=(x﹣y)2+4xy,
因为x﹣y=4,xy=2,
所以(x+y)2=42+4×2=24.
故选:A.
7.根据下列已知条件,能确定△ABC的形状和大小的是( )
A.∠A=50°,∠B=60°,∠C=70° B.∠A=50°,∠B=50°,AB=5cm
C.AB=5cm,AC=4cm,∠B=30° D.AB=6cm,BC=4cm,∠A=30°
解:A、∠A=50°,∠B=60°,∠C=70°,△ABC的形状和大小不能确定,所以A选项不符合题意;
B、∠A=50°,∠B=50°,AB=5cm,则利用“ASA”可判断△ABC是唯一的,所以B选项符合题意;
C、AB=5cm,AC=4cm,∠B=30°,△ABC的形状和大小不能确定,所以C选项不符合题意;
D、AB=6cm,BC=4cm,∠A=30°,△ABC的形状和大小不能确定,所以D选项不符合题意.
故选:B.
8.若一个长方形的周长为20cm,一条边长为xcm(x>0),面积为ycm2,则y与x之间满足的关系式为( )
A.y=x2 B.y=(20﹣x)2 C.y=x?(20﹣x) D.y=x?(10﹣x)
解:∵一个长方形的周长为20cm,一条边长为xcm(x>0),
∴长方形的另一边长为:(10﹣x) cm,
根据题意可得:y=x?(10﹣x).
故选:D.
9.从﹣6,﹣3,0,3,6五个数中任选一个数作为m的值,能使得x2﹣2mx+9是关于x的完全平方式的概率是( )
A. B. C. D.
解:使代数式x2﹣2mx+9是关于x的完全平方式的m的值为±3,
从﹣6,﹣3,0,3,6五个数中任选一个数为3或﹣3的可能性有2种,
所以从﹣6,﹣3,0,3,6五个数中任选一个数作为m的值,能使得x2﹣2mx+9是关于x的完全平方式的概率是,
故选:B.
10.如图,点D在等边△ABC的边CB的延长线上,点E在线段BC上,连接AD,AE,若DA=DE,且∠DAB=20°,那么∠EAC的度数为( )
A.20° B.15° C.10° D.5°
解:∵△ABC为等边三角形,
∴∠ABC=∠BAC=60°,
∵∠ABC=∠D+∠DAB,
∴∠D=60°﹣20°=40°,
∵DA=DE,
∴∠DAE=∠DEA,
∴∠DAE=×(180°﹣∠D)=×(180°﹣40°)=70°,
∴∠EAC=∠DAB+∠BAC﹣∠DAE=20°+60°﹣70°=10°.
故选:C.
二、填空题(本大题共5个小题,每小题3分,共15分,答案写在答题卡上)
11.已知xm=6,xn=2,则xm﹣n= 3 .
解:xm﹣n=xm÷xn=6÷2=3,
故答案为:3.
12.已知y=3﹣2x,则代数式4x2+4xy+y2的值为 9 .
解:4x2+4xy+y2=(2x+y)2,
把y=3﹣2x代入上式,
原式=(2x+3﹣2x)2=9.
故答案为:9.
13.如图,在Rt△ABC中,∠C=90°,AB的垂直平分线DE分别交AB,BC于点F,G,连接AG,若AG平分∠CAB,AC=5,则AB的长为 10 .
解:∵DE是AB的垂直平分线,
∴GA=GB,AF=BF,∠AFE=90°,
∵∠C=90°,AG平分∠CAB,
∴GC=GF,
在Rt△ACG和Rt△AFG中,
,
∴Rt△ACG≌Rt△AFG(HL),
∴AD=AC,
∵AC=5,
∴AF=5,
∴AB=2AF=10,
故答案为:10.
14.若a2﹣5a﹣1=0,则a2+= 27 .
解:∵a2﹣5a﹣1=0,
∴a﹣5﹣=0,
∴a﹣=5,
则(a﹣)2=25,即a2﹣2+=25,
∴a2+=27,
故答案为:27.
15.如图,已知△ABC的面积为36,点D,E分别在边BC,AC上,且BD=CD,CE=2AE,AD与BE相交于点F,若△AEF的面积为3,则图中阴影部分的面积为 9 .
解:连接CF,如图所示.
∵△AEF与△CEF等高,CE=2AE,
∴S△CEF=2S△AEF=2×3=6,
又∵S△ABC=36,BD=CD,
∴S△ABD=S△ACD=S△ABC=18,
∴S△CFD=18﹣3﹣6=9,
又∵△BFD与△CFD同底等高,
故S△BFD=S△CFD=9,
即阴影部分面积为9,
故答案为:9.
三、解答题(本大题共6个小题,共55分,解答过程写在答题卡上)
16.计算:
(1)(﹣2)2﹣(π﹣2021)0+9×()﹣2;
(2)(x+2)(2x﹣5)﹣x(2x﹣1).
解:(1)
=4﹣1+9×
=
=
=3+16
=19.
(2)(x+2)(2x﹣5)﹣x(2x﹣1)
=2x2﹣5x+4x﹣10﹣2x2+x
=﹣10.
17.(1)先化简,再求值:[(2x﹣y)2﹣(x﹣y)(x+y)﹣2y2]÷x,其中x=2,y=﹣3;
(2)已知a为常数,关于x的代数式(x2﹣3x+2)(x2+ax)的化简结果中不含x3项,且(m﹣2)2+|n﹣3|=0,求am﹣n的值
解:(1)原式=(4x2﹣4xy+y2﹣x2+y2﹣2y2)÷x
=(3x2﹣4xy)÷x
=3x﹣4y,
当x=2,y=﹣3时,
原式=3×2﹣4×(﹣3)=6+12=18;
(2)原式=x4+ax3﹣3x3﹣3ax2+2x2+2ax
∵代数式的结果中不含x3项,
∴a﹣3=0,
解得:a=3,
又∵(m﹣2)2+|n﹣3|=0,
∴m﹣2=0,n﹣3=0,
解得:m=2,n=3,
∴am﹣n=32﹣3=3﹣1=.
18.已知:如图,AB∥DE,AC∥DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)过点C作CG⊥AB于点G,若S△ABC=9,DE=6,求CG的长.
【解答】证明:(1)∵BF=CE,
∴BF+CF=CE+CF,
∴BC=EF,
∵AB∥DE,AC∥DF,
∴∠B=∠E,∠ACB=∠DFE=90°,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA);
(2)∵△ABC≌△DEF,
∴AB=DE=6,
∵S△ABC=×AB×CG=9,
∴6CG=18,
∴CG=3.
19.一辆客车和一辆货车沿同一条公路从甲地同时出发驶往乙地,两车均匀速行驶,客车每小时行驶80km,货车每小时行驶60km,货车在途中休息了一段时间后按原速继续匀速行驶,客车直达乙地后原地等待货车到达,两车之间的距离s(km)与货车行驶时间t(h)之间的关系如图所示,请结合图中信息解答下列问题:
(1)填空m的值为 40 ;
(2)试问:货车在途中休息了多长时间?
(3)求当t为何值时,两车相距60km.
解:(1)m=(80﹣60)×2=40(km),
故答案为:40;
(2)行驶两小时后货车在途中休息,休息到t1 h,此时两车相距km,
∴t1=2+(﹣40)÷80=(h),
∴货车在途中休息了﹣2=(h),
答:货车在途中休息了h;
(3)分两种情况①行驶两小时后货车在途中休息时两车相距60km,
t=2+(60﹣40)÷80=(h);
②t2=t1+(100﹣)÷(80﹣60)=3(h),
即客车3h到达乙地,此时两车相距100km,则货车再行驶(100﹣60)km两车相距60km.
∴t=3+(100﹣60)÷60=(h).
答:当t为3h或h时,两车相距60km.
20.已知图1所示的图形是一个轴对称图形,把图1看成一个基本图形,用若干相同的基本图形进行拼图(重合处无缝隙).
(1)如图1,用含a,b的代数式表示c;
(2)如图2,将两个基本图形进行拼图,得到正方形ABCD和正方形EFGH,求阴影部分的面积(用含c的代数式表示);
(3)如图3,将四个基本图形进行拼图,连接其中四个顶点,得到正方形MNPQ,请结合图1,图2的信息直接写出阴影部分的面积(用含c的代数式表示).
解:(1)c=(a﹣b).
(2)如图2中,由题意EF=EH=HG=FG=2c,AB=AD=DC=CB=4c,
∴S阴=(4c)2﹣(2c)2=12c2.
(3)如图2中,由题意,MN==c,
∴S阴=(c)2=10c2.
21.如图,点P是∠MON内部一点,过点P分别作PA∥ON交OM于点A,PB∥OM交ON于点B(PA≥PB),在线段OB上取一点C,连接AC,将△AOC沿直线AC翻折,得到△ADC,延长AD交PB于点E,延长CD交PB于点F.
(1)如图1,当四边形AOBP是正方形时,求证:DF=PF;
(2)如图2,当C为OB中点时,试探究线段AE,AO,BE之间满足的数量关系,并说明理由;
(3)如图3,在(2)的条件下,连接CE,∠ACE的平分线CH交AE于点H,设OA=a,BE=b,若∠CAO=∠CEB,求△CDH的面积(用含a,b的代数式表示).
解:(1)如图1,连接AF,
∵四边形AOBP是正方形,△AOC沿直线AC翻折,得到△ADC,
∴AO=AD=AP,
在Rt△ADF和Rt△APF中,
,
∴Rt△ADF≌Rt△APF(HL),
∴DF=PF;
(2)AE=AO+BE,理由如下:
如图2,延长AC、BF交于点G,
∵C为OB中点,
∴OC=BC,
∵AO∥BP,
∴∠OAC=∠G,∠O=∠CBG,
在△△AOC和△GBC中,
,
∴△AOC≌△GBC(AAS),
∴BG=AO,
∵△AOC沿直线AC翻折,得到△ADC,
∴AO=AD,∠OAC=∠CAE,
∴AD=BG,∠CAE=∠G,
∴△AEG为等腰三角形,
∴AE=EG,
∵GE=AO+BE,
∴AE=AO+BE;
(3)∵AO∥PB,
∴∠OAC+∠CAE+∠CEA+∠CEB=180°,
∵∠ACH+∠ECH+∠CAE+∠CEA=180°,
∴∠OAC+∠CEB=∠ACH+∠ECH,
∵CH平分∠ACE,∠CAO=∠CEB,
∴∠OAC=∠CEB=∠ACH=∠ECH,
又∵∠OAC=∠CAE,
由(2)知∠AEC=∠CEB,
∴∠OAC=∠CEB=∠ACH=∠ECH=∠CAE=∠CEA=45°,
即△ACE是等腰直角三角形,
∵OA=a,BE=b,
∴CH=AH=(a+b),HD=AE﹣DE﹣AH=(a﹣b),
∴△CDH的面积=CH?HD=(a+b)×(a﹣b)=(a2﹣b2).
一、选择题(共10个小题,每小题3分)
1.下列运算正确的是( )
A.x+x2=x3 B.x8÷x2=x4 C.(3x2)2=9x4 D.x3?x2=x6
2.下列各图是选自历届世界大运会的会徽图案,其中是轴对称图形的是( )
A. B. C. D.
3.2020年国产芯片迎来最好的时刻,中芯国际宣布中芯南方厂第一代14纳米FinFET工艺,即中国首条14纳米芯片生产线已成功投产,月产能为3.5万片.其中14纳米=0.000000014米,将数据0.000000014用科学记数法表示为( )
A.1.4×10﹣8 B.14×10﹣8 C.1.4×10﹣9 D.14×10﹣9
4.掷一枚质地均匀的骰子,前3次都是6点朝上,掷第4次时6点朝上的概率是( )
A.1 B. C. D.
5.如图,AB∥CD,∠CEF=61°,那么∠A的度数为( )
A.29° B.61° C.119° D.129°
6.已知x﹣y=4,xy=2,那么(x+y)2的值为( )
A.24 B.20 C.12 D.8
7.根据下列已知条件,能确定△ABC的形状和大小的是( )
A.∠A=50°,∠B=60°,∠C=70° B.∠A=50°,∠B=50°,AB=5cm
C.AB=5cm,AC=4cm,∠B=30° D.AB=6cm,BC=4cm,∠A=30°
8.若一个长方形的周长为20cm,一条边长为xcm(x>0),面积为ycm2,则y与x之间满足的关系式为( )
A.y=x2 B.y=(20﹣x)2 C.y=x?(20﹣x) D.y=x?(10﹣x)
9.从﹣6,﹣3,0,3,6五个数中任选一个数作为m的值,能使得x2﹣2mx+9是关于x的完全平方式的概率是( )
A. B. C. D.
10.如图,点D在等边△ABC的边CB的延长线上,点E在线段BC上,连接AD,AE,若DA=DE,且∠DAB=20°,那么∠EAC的度数为( )
A.20° B.15° C.10° D.5°
二、填空题(本大题共5个小题,每小题3分,共15分,答案写在答题卡上)
11.已知xm=6,xn=2,则xm﹣n= .
12.已知y=3﹣2x,则代数式4x2+4xy+y2的值为 .
13.如图,在Rt△ABC中,∠C=90°,AB的垂直平分线DE分别交AB,BC于点F,G,连接AG,若AG平分∠CAB,AC=5,则AB的长为 .
14.若a2﹣5a﹣1=0,则a2+= .
15.如图,已知△ABC的面积为36,点D,E分别在边BC,AC上,且BD=CD,CE=2AE,AD与BE相交于点F,若△AEF的面积为3,则图中阴影部分的面积为 .
三、解答题(本大题共6个小题,共55分,解答过程写在答题卡上)
16.计算:
(1)(﹣2)2﹣(π﹣2021)0+9×()﹣2;
(2)(x+2)(2x﹣5)﹣x(2x﹣1).
17.(1)先化简,再求值:[(2x﹣y)2﹣(x﹣y)(x+y)﹣2y2]÷x,其中x=2,y=﹣3;
(2)已知a为常数,关于x的代数式(x2﹣3x+2)(x2+ax)的化简结果中不含x3项,且(m﹣2)2+|n﹣3|=0,求am﹣n的值
18.已知:如图,AB∥DE,AC∥DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)过点C作CG⊥AB于点G,若S△ABC=9,DE=6,求CG的长.
19.一辆客车和一辆货车沿同一条公路从甲地同时出发驶往乙地,两车均匀速行驶,客车每小时行驶80km,货车每小时行驶60km,货车在途中休息了一段时间后按原速继续匀速行驶,客车直达乙地后原地等待货车到达,两车之间的距离s(km)与货车行驶时间t(h)之间的关系如图所示,请结合图中信息解答下列问题:
(1)填空m的值为 ;
(2)试问:货车在途中休息了多长时间?
(3)求当t为何值时,两车相距60km.
20.已知图1所示的图形是一个轴对称图形,把图1看成一个基本图形,用若干相同的基本图形进行拼图(重合处无缝隙).
(1)如图1,用含a,b的代数式表示c;
(2)如图2,将两个基本图形进行拼图,得到正方形ABCD和正方形EFGH,求阴影部分的面积(用含c的代数式表示);
(3)如图3,将四个基本图形进行拼图,连接其中四个顶点,得到正方形MNPQ,请结合图1,图2的信息直接写出阴影部分的面积(用含c的代数式表示).
21.如图,点P是∠MON内部一点,过点P分别作PA∥ON交OM于点A,PB∥OM交ON于点B(PA≥PB),在线段OB上取一点C,连接AC,将△AOC沿直线AC翻折,得到△ADC,延长AD交PB于点E,延长CD交PB于点F.
(1)如图1,当四边形AOBP是正方形时,求证:DF=PF;
(2)如图2,当C为OB中点时,试探究线段AE,AO,BE之间满足的数量关系,并说明理由;
(3)如图3,在(2)的条件下,连接CE,∠ACE的平分线CH交AE于点H,设OA=a,BE=b,若∠CAO=∠CEB,求△CDH的面积(用含a,b的代数式表示).
参考答案
一、选择题(本大题共10个小题,每小题3分共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
1.下列运算正确的是( )
A.x+x2=x3 B.x8÷x2=x4 C.(3x2)2=9x4 D.x3?x2=x6
解:A、x与x2不是同类项,不能合并计算,故此选项不符合题意;
B、x8÷x2=x6,故此选项不符合题意;
C、(3x2)2=9x4,正确,故此选项符合题意;
D、x3?x2=x5,故此选项不符合题意;
故选:C.
2.下列各图是选自历届世界大运会的会徽图案,其中是轴对称图形的是( )
A. B. C. D.
解:A.不是轴对称图形,故本选项不合题意;
B.是轴对称图形,故本选项符合题意;
C.不是轴对称图形,故本选项不合题意;
D.不是轴对称图形,故本选项不合题意.
故选:B.
3.2020年国产芯片迎来最好的时刻,中芯国际宣布中芯南方厂第一代14纳米FinFET工艺,即中国首条14纳米芯片生产线已成功投产,月产能为3.5万片.其中14纳米=0.000000014米,将数据0.000000014用科学记数法表示为( )
A.1.4×10﹣8 B.14×10﹣8 C.1.4×10﹣9 D.14×10﹣9
解:0.000000014=1.4×10﹣8.
故选:A.
4.掷一枚质地均匀的骰子,前3次都是6点朝上,掷第4次时6点朝上的概率是( )
A.1 B. C. D.
解:掷一枚质地均匀的骰子,前3次都是6点朝上,
掷第4次时,不会受前3次的影响,
掷第4次时仍有6种等可能出现的结果,其中6点朝上的有1种,
所以掷第4次时6点朝上的概率是,
故选:D.
5.如图,AB∥CD,∠CEF=61°,那么∠A的度数为( )
A.29° B.61° C.119° D.129°
解:∵AB∥CD,
∴∠A+∠AED=180°,
∵∠AED=∠CEF=61°,
∴∠A=180°﹣61°=119°,
故选:C.
6.已知x﹣y=4,xy=2,那么(x+y)2的值为( )
A.24 B.20 C.12 D.8
解:(x+y)2=(x﹣y)2+4xy,
因为x﹣y=4,xy=2,
所以(x+y)2=42+4×2=24.
故选:A.
7.根据下列已知条件,能确定△ABC的形状和大小的是( )
A.∠A=50°,∠B=60°,∠C=70° B.∠A=50°,∠B=50°,AB=5cm
C.AB=5cm,AC=4cm,∠B=30° D.AB=6cm,BC=4cm,∠A=30°
解:A、∠A=50°,∠B=60°,∠C=70°,△ABC的形状和大小不能确定,所以A选项不符合题意;
B、∠A=50°,∠B=50°,AB=5cm,则利用“ASA”可判断△ABC是唯一的,所以B选项符合题意;
C、AB=5cm,AC=4cm,∠B=30°,△ABC的形状和大小不能确定,所以C选项不符合题意;
D、AB=6cm,BC=4cm,∠A=30°,△ABC的形状和大小不能确定,所以D选项不符合题意.
故选:B.
8.若一个长方形的周长为20cm,一条边长为xcm(x>0),面积为ycm2,则y与x之间满足的关系式为( )
A.y=x2 B.y=(20﹣x)2 C.y=x?(20﹣x) D.y=x?(10﹣x)
解:∵一个长方形的周长为20cm,一条边长为xcm(x>0),
∴长方形的另一边长为:(10﹣x) cm,
根据题意可得:y=x?(10﹣x).
故选:D.
9.从﹣6,﹣3,0,3,6五个数中任选一个数作为m的值,能使得x2﹣2mx+9是关于x的完全平方式的概率是( )
A. B. C. D.
解:使代数式x2﹣2mx+9是关于x的完全平方式的m的值为±3,
从﹣6,﹣3,0,3,6五个数中任选一个数为3或﹣3的可能性有2种,
所以从﹣6,﹣3,0,3,6五个数中任选一个数作为m的值,能使得x2﹣2mx+9是关于x的完全平方式的概率是,
故选:B.
10.如图,点D在等边△ABC的边CB的延长线上,点E在线段BC上,连接AD,AE,若DA=DE,且∠DAB=20°,那么∠EAC的度数为( )
A.20° B.15° C.10° D.5°
解:∵△ABC为等边三角形,
∴∠ABC=∠BAC=60°,
∵∠ABC=∠D+∠DAB,
∴∠D=60°﹣20°=40°,
∵DA=DE,
∴∠DAE=∠DEA,
∴∠DAE=×(180°﹣∠D)=×(180°﹣40°)=70°,
∴∠EAC=∠DAB+∠BAC﹣∠DAE=20°+60°﹣70°=10°.
故选:C.
二、填空题(本大题共5个小题,每小题3分,共15分,答案写在答题卡上)
11.已知xm=6,xn=2,则xm﹣n= 3 .
解:xm﹣n=xm÷xn=6÷2=3,
故答案为:3.
12.已知y=3﹣2x,则代数式4x2+4xy+y2的值为 9 .
解:4x2+4xy+y2=(2x+y)2,
把y=3﹣2x代入上式,
原式=(2x+3﹣2x)2=9.
故答案为:9.
13.如图,在Rt△ABC中,∠C=90°,AB的垂直平分线DE分别交AB,BC于点F,G,连接AG,若AG平分∠CAB,AC=5,则AB的长为 10 .
解:∵DE是AB的垂直平分线,
∴GA=GB,AF=BF,∠AFE=90°,
∵∠C=90°,AG平分∠CAB,
∴GC=GF,
在Rt△ACG和Rt△AFG中,
,
∴Rt△ACG≌Rt△AFG(HL),
∴AD=AC,
∵AC=5,
∴AF=5,
∴AB=2AF=10,
故答案为:10.
14.若a2﹣5a﹣1=0,则a2+= 27 .
解:∵a2﹣5a﹣1=0,
∴a﹣5﹣=0,
∴a﹣=5,
则(a﹣)2=25,即a2﹣2+=25,
∴a2+=27,
故答案为:27.
15.如图,已知△ABC的面积为36,点D,E分别在边BC,AC上,且BD=CD,CE=2AE,AD与BE相交于点F,若△AEF的面积为3,则图中阴影部分的面积为 9 .
解:连接CF,如图所示.
∵△AEF与△CEF等高,CE=2AE,
∴S△CEF=2S△AEF=2×3=6,
又∵S△ABC=36,BD=CD,
∴S△ABD=S△ACD=S△ABC=18,
∴S△CFD=18﹣3﹣6=9,
又∵△BFD与△CFD同底等高,
故S△BFD=S△CFD=9,
即阴影部分面积为9,
故答案为:9.
三、解答题(本大题共6个小题,共55分,解答过程写在答题卡上)
16.计算:
(1)(﹣2)2﹣(π﹣2021)0+9×()﹣2;
(2)(x+2)(2x﹣5)﹣x(2x﹣1).
解:(1)
=4﹣1+9×
=
=
=3+16
=19.
(2)(x+2)(2x﹣5)﹣x(2x﹣1)
=2x2﹣5x+4x﹣10﹣2x2+x
=﹣10.
17.(1)先化简,再求值:[(2x﹣y)2﹣(x﹣y)(x+y)﹣2y2]÷x,其中x=2,y=﹣3;
(2)已知a为常数,关于x的代数式(x2﹣3x+2)(x2+ax)的化简结果中不含x3项,且(m﹣2)2+|n﹣3|=0,求am﹣n的值
解:(1)原式=(4x2﹣4xy+y2﹣x2+y2﹣2y2)÷x
=(3x2﹣4xy)÷x
=3x﹣4y,
当x=2,y=﹣3时,
原式=3×2﹣4×(﹣3)=6+12=18;
(2)原式=x4+ax3﹣3x3﹣3ax2+2x2+2ax
∵代数式的结果中不含x3项,
∴a﹣3=0,
解得:a=3,
又∵(m﹣2)2+|n﹣3|=0,
∴m﹣2=0,n﹣3=0,
解得:m=2,n=3,
∴am﹣n=32﹣3=3﹣1=.
18.已知:如图,AB∥DE,AC∥DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)过点C作CG⊥AB于点G,若S△ABC=9,DE=6,求CG的长.
【解答】证明:(1)∵BF=CE,
∴BF+CF=CE+CF,
∴BC=EF,
∵AB∥DE,AC∥DF,
∴∠B=∠E,∠ACB=∠DFE=90°,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(ASA);
(2)∵△ABC≌△DEF,
∴AB=DE=6,
∵S△ABC=×AB×CG=9,
∴6CG=18,
∴CG=3.
19.一辆客车和一辆货车沿同一条公路从甲地同时出发驶往乙地,两车均匀速行驶,客车每小时行驶80km,货车每小时行驶60km,货车在途中休息了一段时间后按原速继续匀速行驶,客车直达乙地后原地等待货车到达,两车之间的距离s(km)与货车行驶时间t(h)之间的关系如图所示,请结合图中信息解答下列问题:
(1)填空m的值为 40 ;
(2)试问:货车在途中休息了多长时间?
(3)求当t为何值时,两车相距60km.
解:(1)m=(80﹣60)×2=40(km),
故答案为:40;
(2)行驶两小时后货车在途中休息,休息到t1 h,此时两车相距km,
∴t1=2+(﹣40)÷80=(h),
∴货车在途中休息了﹣2=(h),
答:货车在途中休息了h;
(3)分两种情况①行驶两小时后货车在途中休息时两车相距60km,
t=2+(60﹣40)÷80=(h);
②t2=t1+(100﹣)÷(80﹣60)=3(h),
即客车3h到达乙地,此时两车相距100km,则货车再行驶(100﹣60)km两车相距60km.
∴t=3+(100﹣60)÷60=(h).
答:当t为3h或h时,两车相距60km.
20.已知图1所示的图形是一个轴对称图形,把图1看成一个基本图形,用若干相同的基本图形进行拼图(重合处无缝隙).
(1)如图1,用含a,b的代数式表示c;
(2)如图2,将两个基本图形进行拼图,得到正方形ABCD和正方形EFGH,求阴影部分的面积(用含c的代数式表示);
(3)如图3,将四个基本图形进行拼图,连接其中四个顶点,得到正方形MNPQ,请结合图1,图2的信息直接写出阴影部分的面积(用含c的代数式表示).
解:(1)c=(a﹣b).
(2)如图2中,由题意EF=EH=HG=FG=2c,AB=AD=DC=CB=4c,
∴S阴=(4c)2﹣(2c)2=12c2.
(3)如图2中,由题意,MN==c,
∴S阴=(c)2=10c2.
21.如图,点P是∠MON内部一点,过点P分别作PA∥ON交OM于点A,PB∥OM交ON于点B(PA≥PB),在线段OB上取一点C,连接AC,将△AOC沿直线AC翻折,得到△ADC,延长AD交PB于点E,延长CD交PB于点F.
(1)如图1,当四边形AOBP是正方形时,求证:DF=PF;
(2)如图2,当C为OB中点时,试探究线段AE,AO,BE之间满足的数量关系,并说明理由;
(3)如图3,在(2)的条件下,连接CE,∠ACE的平分线CH交AE于点H,设OA=a,BE=b,若∠CAO=∠CEB,求△CDH的面积(用含a,b的代数式表示).
解:(1)如图1,连接AF,
∵四边形AOBP是正方形,△AOC沿直线AC翻折,得到△ADC,
∴AO=AD=AP,
在Rt△ADF和Rt△APF中,
,
∴Rt△ADF≌Rt△APF(HL),
∴DF=PF;
(2)AE=AO+BE,理由如下:
如图2,延长AC、BF交于点G,
∵C为OB中点,
∴OC=BC,
∵AO∥BP,
∴∠OAC=∠G,∠O=∠CBG,
在△△AOC和△GBC中,
,
∴△AOC≌△GBC(AAS),
∴BG=AO,
∵△AOC沿直线AC翻折,得到△ADC,
∴AO=AD,∠OAC=∠CAE,
∴AD=BG,∠CAE=∠G,
∴△AEG为等腰三角形,
∴AE=EG,
∵GE=AO+BE,
∴AE=AO+BE;
(3)∵AO∥PB,
∴∠OAC+∠CAE+∠CEA+∠CEB=180°,
∵∠ACH+∠ECH+∠CAE+∠CEA=180°,
∴∠OAC+∠CEB=∠ACH+∠ECH,
∵CH平分∠ACE,∠CAO=∠CEB,
∴∠OAC=∠CEB=∠ACH=∠ECH,
又∵∠OAC=∠CAE,
由(2)知∠AEC=∠CEB,
∴∠OAC=∠CEB=∠ACH=∠ECH=∠CAE=∠CEA=45°,
即△ACE是等腰直角三角形,
∵OA=a,BE=b,
∴CH=AH=(a+b),HD=AE﹣DE﹣AH=(a﹣b),
∴△CDH的面积=CH?HD=(a+b)×(a﹣b)=(a2﹣b2).
同课章节目录
