2021-2022学年湘教版数学九年级上册4.3 解直角三角形---同步课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年湘教版数学九年级上册4.3 解直角三角形---同步课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 899.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览





文档简介
第四章 锐角三角函数
4.3 解直角三角形
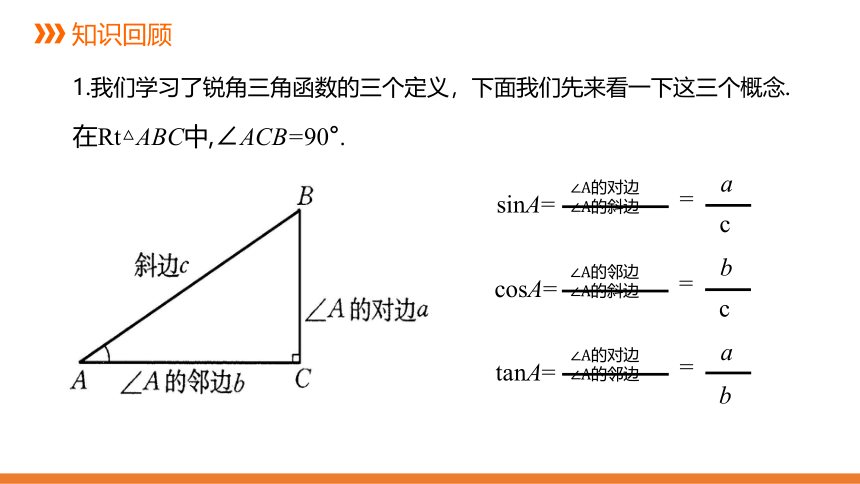
=
a
c
∠A的对边∠A的斜边
?
sinA=
在Rt△ABC中,∠ACB=90°.
=
b
c
∠A的邻边∠A的斜边
?
cosA=
=
a
b
∠A的对边∠A的邻边
?
tanA=
1.我们学习了锐角三角函数的三个定义,下面我们先来看一下这三个概念.
(1)sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角
(注意数形结合,构造直角三角形).
(2)sinA、 cosA、tanA是一个比值(数值).
(3)sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直
角三角形的边长无关.
2.定义中应该注意的几个问题:
在图形的研究中,直角三角形是常见的三角形
之一,因而人们经常会遇到求直角三角形的边长或
角度等问题. 对于这类问题,我们一般利用前面已
学的锐角三角函数的有关知识来解决.
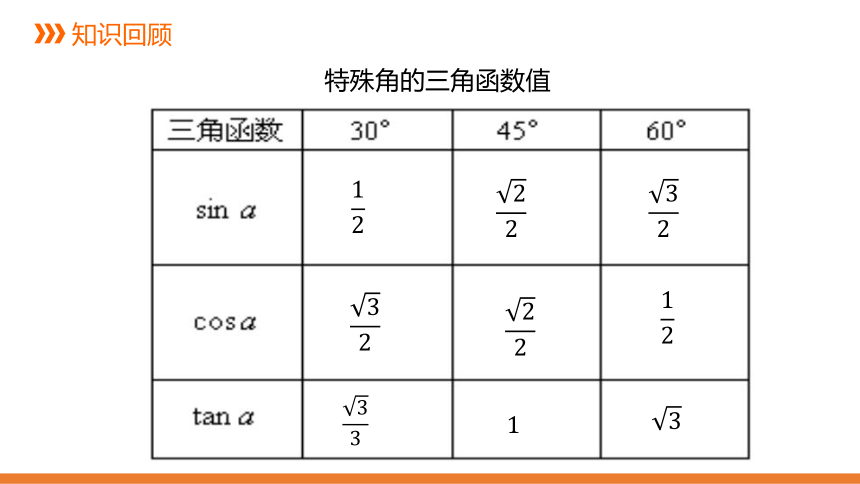
特殊角的三角函数值
12
?
32
?
22
?
12
?
32
?
22
?
33
?
1
?
3
?
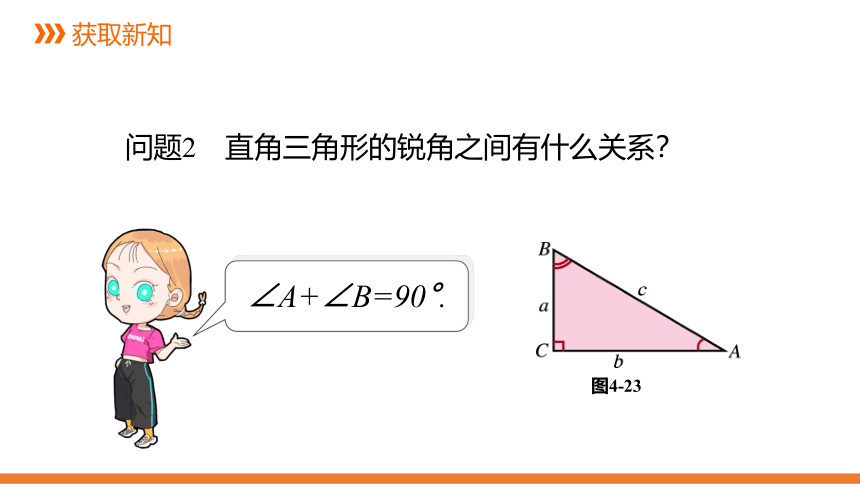
如图4-23,在直角三角形ABC中,∠C=90°,∠A,∠B,∠C的对边分别记作a,b,c .
图4-23
问题1 直角三角形的三边之间有什么关系?
a2+b2=c2(勾股定理)
图4-23
问题2 直角三角形的锐角之间有什么关系?
∠A+∠B=90°.
图4-23
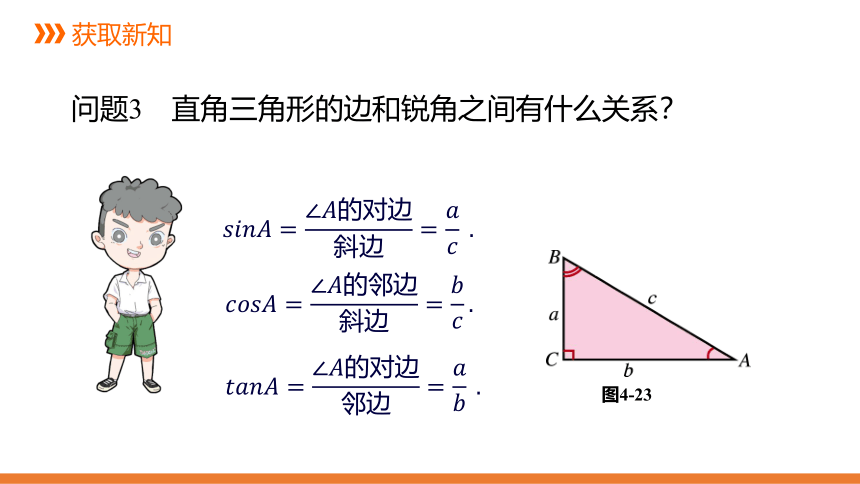
问题3 直角三角形的边和锐角之间有什么关系?
图4-23
????????????????=∠????的对边斜边=?????????.
?
????????????????=∠????的邻边斜边=????????.
?
????????????????=∠????的对边邻边=?????????.
?
如果知道的2个元素都是角,不能求解.因为此时的直角三角形有无数多个.
问题4 在一个直角三角形中,除直角外有5个元素(3条边、2个锐角),要知道其中的几个元素就可以求出其余的元素?
在直角三角形中,除直角外的5个元素(3条边和2个锐角),只要知道其中的2个元素(至少有一个是边),利用上述关系式,就可以求出其余的3个未知元素,把在直角三角形中利用已知元素求其余未知元素的过程叫作解直角三角形.
解直角三角形的依据
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90?;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
★面积公式:
????△????????????=12?????????=12??????
?
例1 如图4-24,在Rt△ABC中,
a=5,求∠B,b,c.
∠????=90°,?∠????=30°?,
?
图4-24
解:
又 ∵
∴
∵
∴
例2 如图,在Rt△ABC 中,∠C=90°,cosA = ,BC = 5, 试求AB的长..
13
?
解:∵∠????=900,????????????????=13,??????∴????????????????=13?????设????????=????,则????????=13????.?????又????????2=????????2+????????2,即????2=13????2+52???????∴????1=1524,????2=?1524(舍去)?????∴????????的长为1524.
?
分析:在直角三角形中,
已知一边和另两边的关系,
常用勾股定理方程思想解决.
图4-24
A
B
例3 在Rt△ABC中,∠C = 90°,a =15.60cm, b=8.50cm,求c,∠A,∠B(长度精确到0.01cm,角度精确到1′).
解:
由于
因此
从而
分析:已知角和线段都不在直角
三角形中,所以需分别延AD、BC,
交于点E,从而解 的直角三角
形ABE即可.
例4 在四边形ABCD中,∠ A= ,AB⊥BC,AD⊥DC,AB=20,CD=10,求AD,BC的长.(保留根号)
60°
E
B
A
C
D
20
10
60°
30°
解:
????????=40?103,????????=203?20
?
30°
在遇到解直角三形的问题时,最好先画一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的,以得于分析解决问题.
选取关系式时要尽量利用原始数据,以防止“累积错误”.
解直角三角形的方法遵循
“有斜用弦,无斜用切;宁乘勿除,化斜为直”.
说说解直角三角形时,有哪些注意点?
1. 在Rt△ABC中, b=3cm,
求∠A,a,c (精确到0.01cm).
∠????=90°,?∠????=45°?,
?
答:
2. 在Rt△ABC中, a=5.82cm,c=9.60cm,
求b,∠A ,∠B (角度精确到1′,长度精确到 0.01cm).
∠????=90°,
?
答:
3. 在Rt△ABC中, c = 15.68cm,
求∠B , a,b (长度精确到 0.01cm).
∠????=90°,∠????=30°,
?
答:
4. 如图,根据图中已知数据,求△ABC其余各边的长, 各角的度数和△ABC的面积.
A
B
C
450
300
4
解:??
?????????=42,????????=2(2+6),
∠????????????=105°
????????????????????=4+43
4.3 解直角三角形
=
a
c
∠A的对边∠A的斜边
?
sinA=
在Rt△ABC中,∠ACB=90°.
=
b
c
∠A的邻边∠A的斜边
?
cosA=
=
a
b
∠A的对边∠A的邻边
?
tanA=
1.我们学习了锐角三角函数的三个定义,下面我们先来看一下这三个概念.
(1)sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角
(注意数形结合,构造直角三角形).
(2)sinA、 cosA、tanA是一个比值(数值).
(3)sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直
角三角形的边长无关.
2.定义中应该注意的几个问题:
在图形的研究中,直角三角形是常见的三角形
之一,因而人们经常会遇到求直角三角形的边长或
角度等问题. 对于这类问题,我们一般利用前面已
学的锐角三角函数的有关知识来解决.
特殊角的三角函数值
12
?
32
?
22
?
12
?
32
?
22
?
33
?
1
?
3
?
如图4-23,在直角三角形ABC中,∠C=90°,∠A,∠B,∠C的对边分别记作a,b,c .
图4-23
问题1 直角三角形的三边之间有什么关系?
a2+b2=c2(勾股定理)
图4-23
问题2 直角三角形的锐角之间有什么关系?
∠A+∠B=90°.
图4-23
问题3 直角三角形的边和锐角之间有什么关系?
图4-23
????????????????=∠????的对边斜边=?????????.
?
????????????????=∠????的邻边斜边=????????.
?
????????????????=∠????的对边邻边=?????????.
?
如果知道的2个元素都是角,不能求解.因为此时的直角三角形有无数多个.
问题4 在一个直角三角形中,除直角外有5个元素(3条边、2个锐角),要知道其中的几个元素就可以求出其余的元素?
在直角三角形中,除直角外的5个元素(3条边和2个锐角),只要知道其中的2个元素(至少有一个是边),利用上述关系式,就可以求出其余的3个未知元素,把在直角三角形中利用已知元素求其余未知元素的过程叫作解直角三角形.
解直角三角形的依据
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90?;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
★面积公式:
????△????????????=12?????????=12??????
?
例1 如图4-24,在Rt△ABC中,
a=5,求∠B,b,c.
∠????=90°,?∠????=30°?,
?
图4-24
解:
又 ∵
∴
∵
∴
例2 如图,在Rt△ABC 中,∠C=90°,cosA = ,BC = 5, 试求AB的长..
13
?
解:∵∠????=900,????????????????=13,??????∴????????????????=13?????设????????=????,则????????=13????.?????又????????2=????????2+????????2,即????2=13????2+52???????∴????1=1524,????2=?1524(舍去)?????∴????????的长为1524.
?
分析:在直角三角形中,
已知一边和另两边的关系,
常用勾股定理方程思想解决.
图4-24
A
B
例3 在Rt△ABC中,∠C = 90°,a =15.60cm, b=8.50cm,求c,∠A,∠B(长度精确到0.01cm,角度精确到1′).
解:
由于
因此
从而
分析:已知角和线段都不在直角
三角形中,所以需分别延AD、BC,
交于点E,从而解 的直角三角
形ABE即可.
例4 在四边形ABCD中,∠ A= ,AB⊥BC,AD⊥DC,AB=20,CD=10,求AD,BC的长.(保留根号)
60°
E
B
A
C
D
20
10
60°
30°
解:
????????=40?103,????????=203?20
?
30°
在遇到解直角三形的问题时,最好先画一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的,以得于分析解决问题.
选取关系式时要尽量利用原始数据,以防止“累积错误”.
解直角三角形的方法遵循
“有斜用弦,无斜用切;宁乘勿除,化斜为直”.
说说解直角三角形时,有哪些注意点?
1. 在Rt△ABC中, b=3cm,
求∠A,a,c (精确到0.01cm).
∠????=90°,?∠????=45°?,
?
答:
2. 在Rt△ABC中, a=5.82cm,c=9.60cm,
求b,∠A ,∠B (角度精确到1′,长度精确到 0.01cm).
∠????=90°,
?
答:
3. 在Rt△ABC中, c = 15.68cm,
求∠B , a,b (长度精确到 0.01cm).
∠????=90°,∠????=30°,
?
答:
4. 如图,根据图中已知数据,求△ABC其余各边的长, 各角的度数和△ABC的面积.
A
B
C
450
300
4
解:??
?????????=42,????????=2(2+6),
∠????????????=105°
????????????????????=4+43
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
