2021-2022学年湘教版数学九年级上册4.4 解直角三角形的应用-2 同步课件(17张PPT)
文档属性
| 名称 | 2021-2022学年湘教版数学九年级上册4.4 解直角三角形的应用-2 同步课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 672.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 16:50:19 | ||
图片预览






文档简介
第四章 锐角三角函数
4.4 解直角三角形的应用
第2课时 与坡度、方向角有关的实际问题
2.两锐角之间的关系呢?
∠A+∠B=90°
1.三边之间的关系是什么?
????2+????2=????2
?
A
B
a
b
c
C
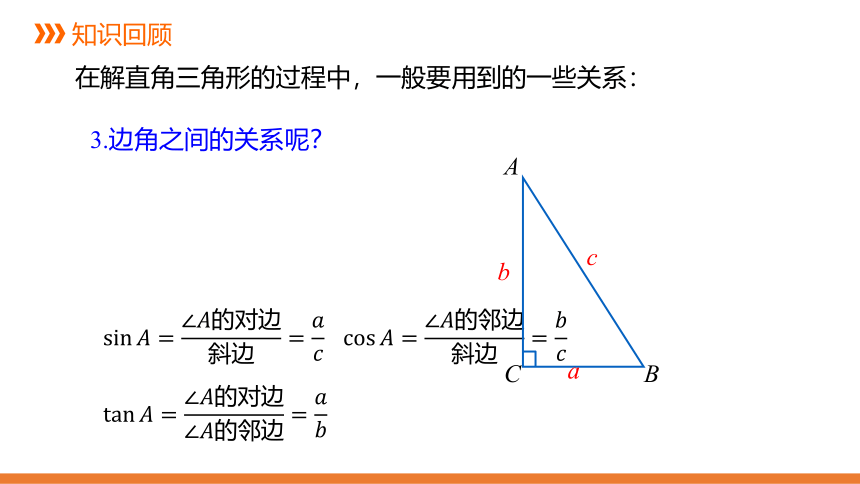
在解直角三角形的过程中,一般要用到的一些关系:
3.边角之间的关系呢?
sin????=∠????的对边斜边=????????
?
cos????=∠????的邻边斜边=????????
?
tan????=∠????的对边∠????的邻边=????????
?
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到的一些关系:
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
如图4-18, 从山脚到山顶有两条路AB与BD, 问哪条路比较陡?
右边的路BD陡些.如何用数量来刻画哪条路陡呢?
在图4-19 中, ∠BAC 叫作坡角.
坡角:坡面与地平面的夹角α叫坡角.
坡度(坡比): 如图,坡面的高度h 和 水平距离l 的比
叫坡度(或坡比),用字母i表示, 即
????=????????????????=?????
?
(坡度通常写成1 ∶ m的形式).
坡度越大,山坡越陡.
B
C
A
例1 如图4-20, 一山坡的坡度为i = 1∶2 . 小刚从山脚A 出发, 沿山坡向上走了240 m 到达点C. 这座山坡的坡角是多少度? 小刚上升了多少米? (角度精确到0.01°,长度精确到0.1 m)
●
●
B
C
A
●
●
分析:在直角三角形ABC中,已知了坡度即角α的正切可求出坡角α,然后用α的正弦求出对边BC的长.
解:用α 表示坡角的大小, 由题意可得
,
因此α ≈26.57°.
在Rt△ABC中,
∠B =90°, ∠A = 26.57°, AC =240 ,
因此
从而BC = 240 ×sin 26.57°≈107.3(m).
答:这座山坡的坡角约为26.57°,小刚上升了约107.3 m.
????????????????=12=0.5
?
????????????????=????????????????=????????240.
?
如图,拦水坝的横断面为梯形ABCD,根据图中数据求坡角a和β;
B
A
D
F
E
C
6m
α
β
i=1:3
i=1:1.5
解:在Rt△AFB中,∠AFB=90°
tan????=????????????????=????=1:1.5
?
????≈33.7?
?
在Rt△CDE中,∠CED=90°
tan????=????????????????=????=1:3
?
????≈18.4?
?
B
A
D
F
E
C
6m
α
β
i=1:3
i=1:1.5
例2 如图4-21, 一艘船以40 km/h 的速度向正东航行, 在A 处测得灯塔C 在北偏东60°方向上, 继续航行1 h到达B 处,这时测得灯塔C 在北偏东30°方向上. 已知在灯塔C的四周30 km内有暗礁.问这艘船继续向东航行是否安全?
分析:在两个直角三角形中,分别利用300 、 600角的正切,用同一个参量x表示出AD 、 BD的长,进而用方程思想求解.
解:作CD⊥AB, 交AB延长线于点D. 设CD = x.
在Rt△ACD中,
∵????????????∠????????????=????????????????,∴????????=????????????????????∠????????????=????????????????300.同理,在????????????????????????中,????????=????????????????????∠????????????=????????????????600.∵????????=?????????????????,∴????????????????300?????????????????600=40.解得????????=203又203≈34.64>30.
?
因此,该船能继续安全地向东航行.
100
1.什么是坡比?
2.东北方向指北偏东多少度?
3.说说利用解直角三角形的知识解决实际问题的一般过程是什么?
(1)将实际问题抽象为数学问题
(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案,从而得到实际问题的答案.
4.4 解直角三角形的应用
第2课时 与坡度、方向角有关的实际问题
2.两锐角之间的关系呢?
∠A+∠B=90°
1.三边之间的关系是什么?
????2+????2=????2
?
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到的一些关系:
3.边角之间的关系呢?
sin????=∠????的对边斜边=????????
?
cos????=∠????的邻边斜边=????????
?
tan????=∠????的对边∠????的邻边=????????
?
A
B
a
b
c
C
在解直角三角形的过程中,一般要用到的一些关系:
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
如图4-18, 从山脚到山顶有两条路AB与BD, 问哪条路比较陡?
右边的路BD陡些.如何用数量来刻画哪条路陡呢?
在图4-19 中, ∠BAC 叫作坡角.
坡角:坡面与地平面的夹角α叫坡角.
坡度(坡比): 如图,坡面的高度h 和 水平距离l 的比
叫坡度(或坡比),用字母i表示, 即
????=????????????????=?????
?
(坡度通常写成1 ∶ m的形式).
坡度越大,山坡越陡.
B
C
A
例1 如图4-20, 一山坡的坡度为i = 1∶2 . 小刚从山脚A 出发, 沿山坡向上走了240 m 到达点C. 这座山坡的坡角是多少度? 小刚上升了多少米? (角度精确到0.01°,长度精确到0.1 m)
●
●
B
C
A
●
●
分析:在直角三角形ABC中,已知了坡度即角α的正切可求出坡角α,然后用α的正弦求出对边BC的长.
解:用α 表示坡角的大小, 由题意可得
,
因此α ≈26.57°.
在Rt△ABC中,
∠B =90°, ∠A = 26.57°, AC =240 ,
因此
从而BC = 240 ×sin 26.57°≈107.3(m).
答:这座山坡的坡角约为26.57°,小刚上升了约107.3 m.
????????????????=12=0.5
?
????????????????=????????????????=????????240.
?
如图,拦水坝的横断面为梯形ABCD,根据图中数据求坡角a和β;
B
A
D
F
E
C
6m
α
β
i=1:3
i=1:1.5
解:在Rt△AFB中,∠AFB=90°
tan????=????????????????=????=1:1.5
?
????≈33.7?
?
在Rt△CDE中,∠CED=90°
tan????=????????????????=????=1:3
?
????≈18.4?
?
B
A
D
F
E
C
6m
α
β
i=1:3
i=1:1.5
例2 如图4-21, 一艘船以40 km/h 的速度向正东航行, 在A 处测得灯塔C 在北偏东60°方向上, 继续航行1 h到达B 处,这时测得灯塔C 在北偏东30°方向上. 已知在灯塔C的四周30 km内有暗礁.问这艘船继续向东航行是否安全?
分析:在两个直角三角形中,分别利用300 、 600角的正切,用同一个参量x表示出AD 、 BD的长,进而用方程思想求解.
解:作CD⊥AB, 交AB延长线于点D. 设CD = x.
在Rt△ACD中,
∵????????????∠????????????=????????????????,∴????????=????????????????????∠????????????=????????????????300.同理,在????????????????????????中,????????=????????????????????∠????????????=????????????????600.∵????????=?????????????????,∴????????????????300?????????????????600=40.解得????????=203又203≈34.64>30.
?
因此,该船能继续安全地向东航行.
100
1.什么是坡比?
2.东北方向指北偏东多少度?
3.说说利用解直角三角形的知识解决实际问题的一般过程是什么?
(1)将实际问题抽象为数学问题
(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角形函数等去解直角三角形;
(3)得到数学问题的答案,从而得到实际问题的答案.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
