2021-2022学年湘教版数学九年级上册3.1.2 成比例线段-同步课件(29张PPT)
文档属性
| 名称 | 2021-2022学年湘教版数学九年级上册3.1.2 成比例线段-同步课件(29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 609.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览






文档简介
第三章 图形的相似
3.1.2 成比例线段
我们知道线段既有形状又有大小,这节课我们主要研究线段之间的数量关系,并由数量关系带给我们对图形形状的思考!
引入
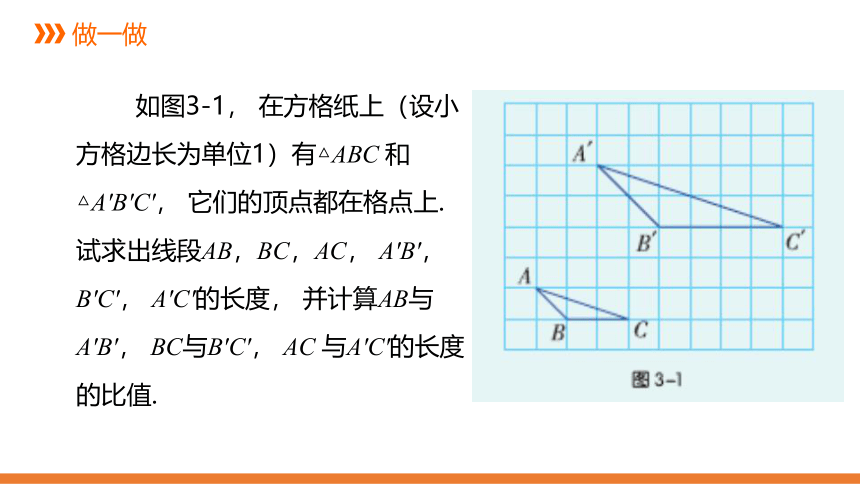
如图3-1, 在方格纸上(设小方格边长为单位1)有△ABC 和△A′B′C′, 它们的顶点都在格点上. 试求出线段AB,BC,AC, A′B′, B′C′, A′C′的长度, 并计算AB与A′B′, BC与B′C′, AC 与A′C′的长度的比值.
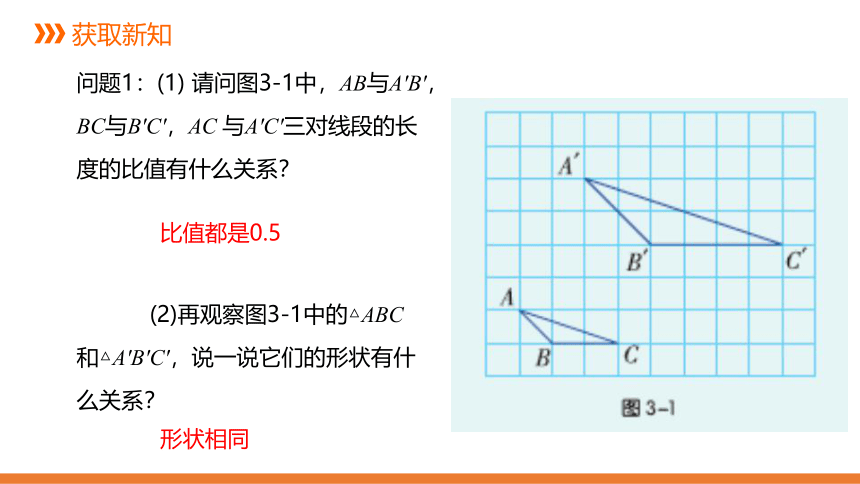
问题1:(1) 请问图3-1中,AB与A′B′, BC与B′C′,AC 与A′C′三对线段的长度的比值有什么关系?
(2)再观察图3-1中的△ABC 和△A′B′C′,说一说它们的形状有什么关系?
比值都是0.5
形状相同
定义1:一般地, 如果选用同一长度单位量得两条线段AB, A′B′的长度分别为m,n, 那么把它们的长度的比 叫作这两条线段AB与A′B′的比(ratio), 记作
或 AB ∶ A′B′= m ∶ n ;
如果 的比值为k,那么上述式子也可写成
或 AB = k·A′B′ .
????????
?
????????????′????′=????????
?
????????????′????′=????
?
????????
?
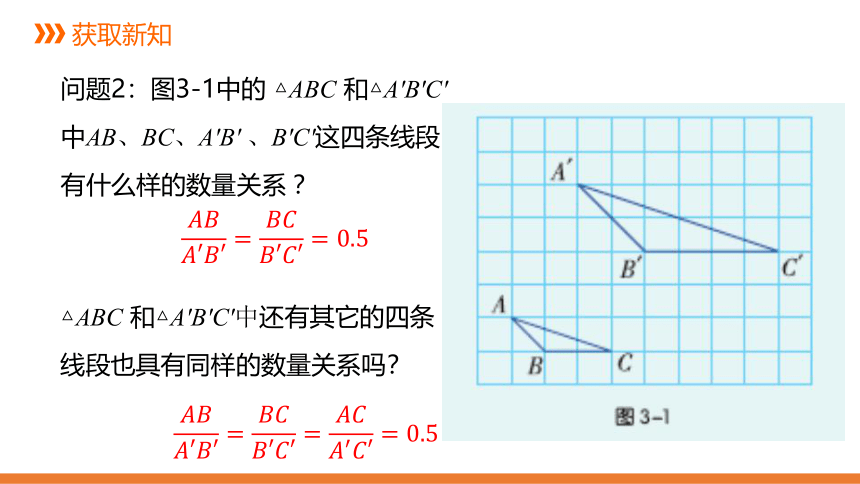
问题2:图3-1中的 △ABC 和△A′B′C′中AB、BC、A′B′ 、B′C′这四条线段有什么样的数量关系 ?
△ABC 和△A′B′C′中还有其它的四条线段也具有同样的数量关系吗?
????????????′????′=????????????′????′=0.5
?
????????????′????′=????????????′????′=????????????′????′=0.5
?
定义2:
在四条线段中, 如果其中两条线段的比等于另外两条线段的比, 那么这四条线段叫作成比例线段, 简称为比例线段.
例3 (1)已知线段a,b,c,d 的长度分别为0.8cm,2cm,1.2cm, 3cm,问a,b,c,d是比例线段吗?
解 (一) ∵
∴ , 即a, b, c, d 是比例线段.
????????=0.82=0.4??,??????????=1.23=0.4,
?
????????=????????
?
解(二) ∵
????????=0.81.2=23,????????=23,
?
????????=????????
?
∴ , 即a, b, c, d 是比例线段.
例3 (2)已知线段a,b,c,d是比例线段,其中a,b,c的长度分别为0.8cm,2cm,1.2cm,求d.
解 ∵线段a,b,c,d是比例线段,
∴ 或 或 ;
????????=????????
?
????????=????????
?
????????=????????
?
当 时,代入已知数,解得 d=3cm;
????????=????????
?
当 时,代入已知数,解得, d=0.48cm;
????????=????????
?
当 时,代入已知数,解得, d= cm.
????????=????????
?
43
?
问题3:你能画出成比例线段吗?
思路(1).
由例3的启发,画长度分别是1cm、2cm、3cm、6cm的四条线段,这样的四条线段是成比例线段;
当然长度分别为1cm、2cm、2cm、4cm的四条线段是成比例线段。
解 ∵ 平行四边形ABCD,
∴ AB=CD,BC=AD;
∴ 或 ;
∴ AB、BC、CD、DA四条线段是成比例线段.
思路(2).
如图, 平行四边形ABCD中的 四条线段是成比例线段
????????????????=????????????????
?
????????????????=????????????????=1
?
当然矩形、正方形、菱形中的四条线段也分别都是成比例线段.比值都为 1.
问题4 :古希腊数学家、天文学家欧多克索斯(约400—约前347)曾经提出一个问题:能否将一条线段AB分成不相等的两部分,使较短线段CB 与较长线段AC的比等于线段AC与原线段AB的比?
即,如图,使得
????????????????=????????????????
?
成立?
解决方法:
????????????????=????????????????
?
由等式
,得
1?????????=????1
?
解得 (舍去).
????1=5?12
?
????2=?5?12
?
因此
5?12≈0.618.
?
????????????????=
?
先把问题特殊化, 设线段AB的长度为1个单位, 点C为线段AB上一点,且AC的长度为x个单位,则CB的长度为(1- x )个单位.
小结:借助方程的知识,我们知道在一个单位长度的线段上存在一点将其分成不相等的两部分,其中较短的线段与较长的线段的比等于较长线段与原线段的比,
而且比值等于 .
5?12≈0.618
?
问题5:
如果能的话,这个比值会是 吗?
5?12≈0.618
?
对于任意长度的线段是否存在一点将其分成不相等的 两部分,其中较短的线段与较长的线段的比等于较长线段与原线段的比吗?
解决方法:
设线段AB 的长度为a 个单位,点C为线段AB 上一点,且AC的长度为x个单位,则CB的长度为(a-x )个单位.
????????????????=????????????????
?
由等式
,得
?????????????=????????
?
(参考特殊方法,把特殊值1变成任意值a)
????????????????=????1????=5?12≈0.618
?
因此, .
解得 (舍去).
????1=5?????????2,????2=?5?????????2
?
小结:借助方程的知识,我们知道在任意长度的线段上也存在一点将其分成不相等的两部分,其中较短的线段与较长的线段的比等于较长线段与原线段的比,
而且比值也等于
5?12≈0.618
?
定义3:
如果能将一条线段AB分成不相等的两部分,使较短线段CB与较长线段AC的比等于线段AC与原线段AB的比,那么称线段AB被点C黄金分割(golden section),点C叫作线段AB的黄金分割点, 较长线段AC与原线段AB的比叫作黄金分割比.
问题6:我们知道任意线段都有黄金分割点,那如何找到它呢?
对于一条给定的线段AB,找出它的黄金分割点的作法如下:
(1)过点B作AB的垂线,并在垂线上取BC= AB;
12
?
(2)连接AC,以点C为圆心,CB为半径画弧,交AC于点E;
(3)以点A为圆心,AE为半径画弧,交AB 于点P.
则点P为所求作的线段AB的黄金分割点.
欣赏:我们知道黄金分割比是个确定数
,这个数可是享誉全世界的,因为比值是它的线段围成的图形是最美丽的图形.
5?12≈0.618
?
古希腊的巴台农神庙正面高度与底部宽度之比约为黄金分割比.
印度泰姬陵正面高度与底部宽度之比约为黄金分割比.
意大利著名画家达·芬奇的名作《蒙娜丽莎》中, 人物的脸的宽度与高度的比就是一个黄金分割比.
C
B
1、请问同学们这节课你学习了关于线段的什么知识?
线段之间的一种数量关系:四条线段成比例.
并且感受到成比例线段围成的图形在形状上也有美妙的关系!
认识了一个最特别的数 ,比值是它的线段围成的图形最美丽.
?????????????≈????.????????????
?
2、请问同学们以前学过的哪些图形中有成比例线段?
平行四边形、矩形、正方形、菱形中的四条线段分别都是成比例线段.
3、请问同学们你有哪些方法画比例线段?
(2)可以画平行四边形、矩形、正方形或菱形.
(1)可以先确定比例线段的长度再画线段;
3.1.2 成比例线段
我们知道线段既有形状又有大小,这节课我们主要研究线段之间的数量关系,并由数量关系带给我们对图形形状的思考!
引入
如图3-1, 在方格纸上(设小方格边长为单位1)有△ABC 和△A′B′C′, 它们的顶点都在格点上. 试求出线段AB,BC,AC, A′B′, B′C′, A′C′的长度, 并计算AB与A′B′, BC与B′C′, AC 与A′C′的长度的比值.
问题1:(1) 请问图3-1中,AB与A′B′, BC与B′C′,AC 与A′C′三对线段的长度的比值有什么关系?
(2)再观察图3-1中的△ABC 和△A′B′C′,说一说它们的形状有什么关系?
比值都是0.5
形状相同
定义1:一般地, 如果选用同一长度单位量得两条线段AB, A′B′的长度分别为m,n, 那么把它们的长度的比 叫作这两条线段AB与A′B′的比(ratio), 记作
或 AB ∶ A′B′= m ∶ n ;
如果 的比值为k,那么上述式子也可写成
或 AB = k·A′B′ .
????????
?
????????????′????′=????????
?
????????????′????′=????
?
????????
?
问题2:图3-1中的 △ABC 和△A′B′C′中AB、BC、A′B′ 、B′C′这四条线段有什么样的数量关系 ?
△ABC 和△A′B′C′中还有其它的四条线段也具有同样的数量关系吗?
????????????′????′=????????????′????′=0.5
?
????????????′????′=????????????′????′=????????????′????′=0.5
?
定义2:
在四条线段中, 如果其中两条线段的比等于另外两条线段的比, 那么这四条线段叫作成比例线段, 简称为比例线段.
例3 (1)已知线段a,b,c,d 的长度分别为0.8cm,2cm,1.2cm, 3cm,问a,b,c,d是比例线段吗?
解 (一) ∵
∴ , 即a, b, c, d 是比例线段.
????????=0.82=0.4??,??????????=1.23=0.4,
?
????????=????????
?
解(二) ∵
????????=0.81.2=23,????????=23,
?
????????=????????
?
∴ , 即a, b, c, d 是比例线段.
例3 (2)已知线段a,b,c,d是比例线段,其中a,b,c的长度分别为0.8cm,2cm,1.2cm,求d.
解 ∵线段a,b,c,d是比例线段,
∴ 或 或 ;
????????=????????
?
????????=????????
?
????????=????????
?
当 时,代入已知数,解得 d=3cm;
????????=????????
?
当 时,代入已知数,解得, d=0.48cm;
????????=????????
?
当 时,代入已知数,解得, d= cm.
????????=????????
?
43
?
问题3:你能画出成比例线段吗?
思路(1).
由例3的启发,画长度分别是1cm、2cm、3cm、6cm的四条线段,这样的四条线段是成比例线段;
当然长度分别为1cm、2cm、2cm、4cm的四条线段是成比例线段。
解 ∵ 平行四边形ABCD,
∴ AB=CD,BC=AD;
∴ 或 ;
∴ AB、BC、CD、DA四条线段是成比例线段.
思路(2).
如图, 平行四边形ABCD中的 四条线段是成比例线段
????????????????=????????????????
?
????????????????=????????????????=1
?
当然矩形、正方形、菱形中的四条线段也分别都是成比例线段.比值都为 1.
问题4 :古希腊数学家、天文学家欧多克索斯(约400—约前347)曾经提出一个问题:能否将一条线段AB分成不相等的两部分,使较短线段CB 与较长线段AC的比等于线段AC与原线段AB的比?
即,如图,使得
????????????????=????????????????
?
成立?
解决方法:
????????????????=????????????????
?
由等式
,得
1?????????=????1
?
解得 (舍去).
????1=5?12
?
????2=?5?12
?
因此
5?12≈0.618.
?
????????????????=
?
先把问题特殊化, 设线段AB的长度为1个单位, 点C为线段AB上一点,且AC的长度为x个单位,则CB的长度为(1- x )个单位.
小结:借助方程的知识,我们知道在一个单位长度的线段上存在一点将其分成不相等的两部分,其中较短的线段与较长的线段的比等于较长线段与原线段的比,
而且比值等于 .
5?12≈0.618
?
问题5:
如果能的话,这个比值会是 吗?
5?12≈0.618
?
对于任意长度的线段是否存在一点将其分成不相等的 两部分,其中较短的线段与较长的线段的比等于较长线段与原线段的比吗?
解决方法:
设线段AB 的长度为a 个单位,点C为线段AB 上一点,且AC的长度为x个单位,则CB的长度为(a-x )个单位.
????????????????=????????????????
?
由等式
,得
?????????????=????????
?
(参考特殊方法,把特殊值1变成任意值a)
????????????????=????1????=5?12≈0.618
?
因此, .
解得 (舍去).
????1=5?????????2,????2=?5?????????2
?
小结:借助方程的知识,我们知道在任意长度的线段上也存在一点将其分成不相等的两部分,其中较短的线段与较长的线段的比等于较长线段与原线段的比,
而且比值也等于
5?12≈0.618
?
定义3:
如果能将一条线段AB分成不相等的两部分,使较短线段CB与较长线段AC的比等于线段AC与原线段AB的比,那么称线段AB被点C黄金分割(golden section),点C叫作线段AB的黄金分割点, 较长线段AC与原线段AB的比叫作黄金分割比.
问题6:我们知道任意线段都有黄金分割点,那如何找到它呢?
对于一条给定的线段AB,找出它的黄金分割点的作法如下:
(1)过点B作AB的垂线,并在垂线上取BC= AB;
12
?
(2)连接AC,以点C为圆心,CB为半径画弧,交AC于点E;
(3)以点A为圆心,AE为半径画弧,交AB 于点P.
则点P为所求作的线段AB的黄金分割点.
欣赏:我们知道黄金分割比是个确定数
,这个数可是享誉全世界的,因为比值是它的线段围成的图形是最美丽的图形.
5?12≈0.618
?
古希腊的巴台农神庙正面高度与底部宽度之比约为黄金分割比.
印度泰姬陵正面高度与底部宽度之比约为黄金分割比.
意大利著名画家达·芬奇的名作《蒙娜丽莎》中, 人物的脸的宽度与高度的比就是一个黄金分割比.
C
B
1、请问同学们这节课你学习了关于线段的什么知识?
线段之间的一种数量关系:四条线段成比例.
并且感受到成比例线段围成的图形在形状上也有美妙的关系!
认识了一个最特别的数 ,比值是它的线段围成的图形最美丽.
?????????????≈????.????????????
?
2、请问同学们以前学过的哪些图形中有成比例线段?
平行四边形、矩形、正方形、菱形中的四条线段分别都是成比例线段.
3、请问同学们你有哪些方法画比例线段?
(2)可以画平行四边形、矩形、正方形或菱形.
(1)可以先确定比例线段的长度再画线段;
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
