2021-2022学年湘教版数学九年级上册3.2 平行线分线段成比例-同步课件(27张PPT)
文档属性
| 名称 | 2021-2022学年湘教版数学九年级上册3.2 平行线分线段成比例-同步课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览






文档简介
第三章 图形的相似
3.2 平行线分线段成比例
在四条线段中, 如果其中两条线段的比等于另外两条线段的比, 那么这四条线段叫作成比例线段, 简称为比例线段.
平行四边形、矩形、正方形、菱形中的四条线段也分别都是成比例线段.
如果能将一条线段AB分成不相等的两部分,使较短线段CB与较长线段AC的比等于线段AC与原线段AB的比,那么称线段AB被点C黄金分割(golden section),点C叫作线段AB的黄金分割点, 较长线段AC与原线段AB的比叫作黄金分割比.
任意线段都有黄金分割点,如何找到它呢?
对于一条给定的线段AB,找出它的黄金分割点的作法如下:
(1)过点B作AB的垂线,并在垂线上取BC= AB;
(2)连接AC,以点C为圆心,CB为半径画弧,交AC于点E;
(3)以点A为圆心,AE为半径画弧,交AB 于点P.
则点P为所求作的线段AB的黄金分割点.
互相平行
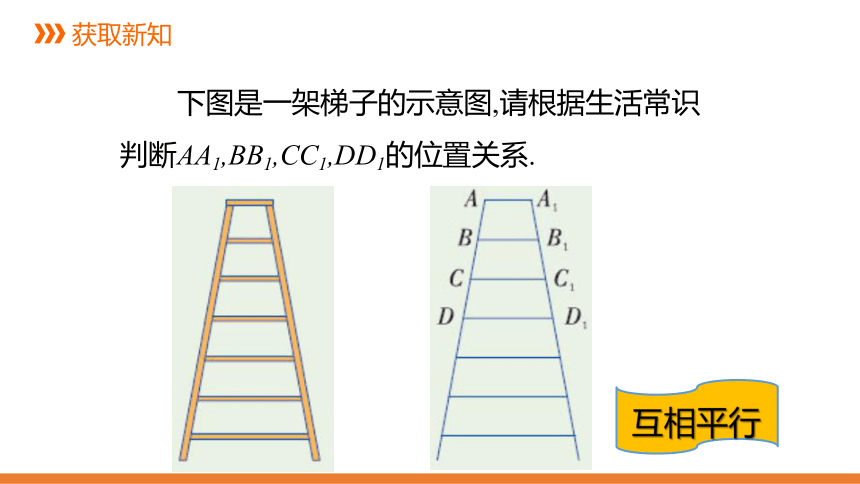
下图是一架梯子的示意图,请根据生活常识判断AA1,BB1,CC1,DD1的位置关系.
a
b
c
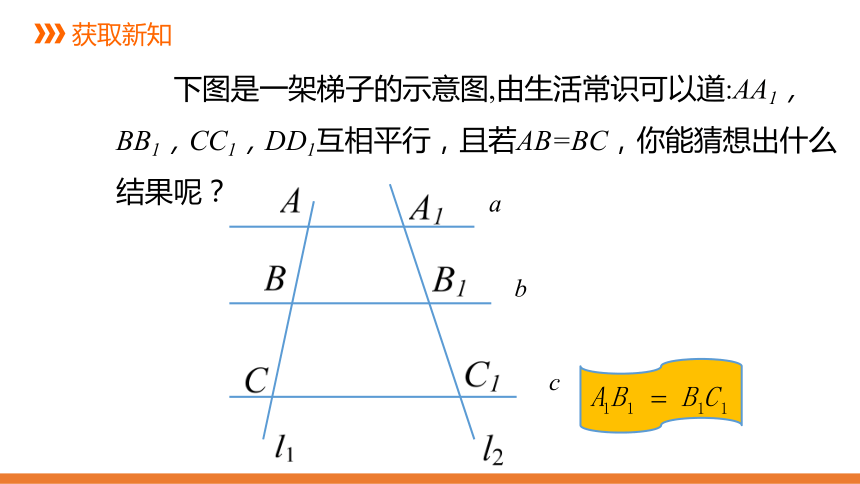
下图是一架梯子的示意图,由生活常识可以道:AA1,BB1,CC1,DD1互相平行,且若AB=BC,你能猜想出什么结果呢?
a
b
c
如图,已知直线a∥b∥c.直线l1,l2被直线a,b,c截得的线段分别为AB,BC和A1B1,B1C1,且AB=BC,要证明A1B1=B1C1,能不做辅助线证明吗?如果必须做辅助线,你考虑怎么做呢?
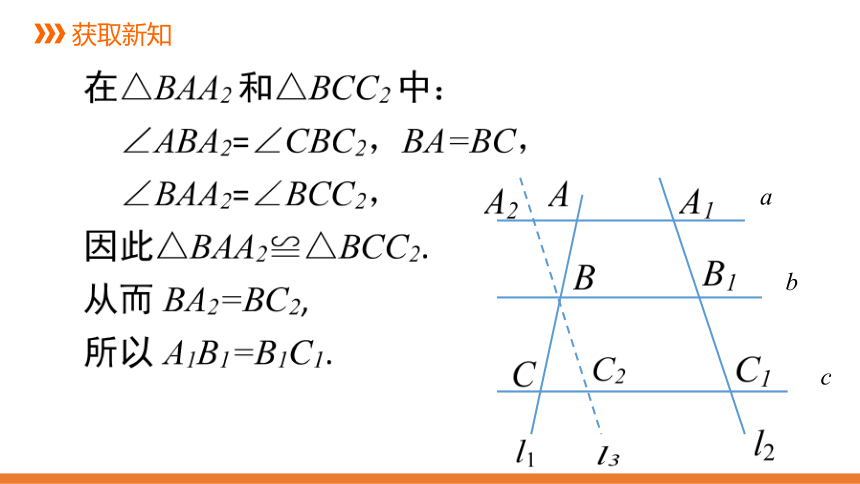
过点B作直线l3//l2,分别与直线a,c相交于点A2,C2,由于a//b//c,l3//l2,因此由
“夹在两平行线间的
平行线段相等”可知
A2B=A1B1,
BC2=B1C1.
a
b
c
a
b
c
两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
a
b
c
相等,都等于1.
a
b
c
,则把线段AB二等分,分点D.
过点D作直线d∥a,交l2于点D1.如图:
把线段BC三等分.
三等分点为E,F,分
别过点E,F作直线
e∥a,f∥a,分别交
l2于点E1,F1.
e
a
b
c
f
d
证明:
e
a
b
c
f
d
a
b
c
两条直线被一组直线所截,所得的对应线段成比例.
我们把以上基本事实简称为平行线分线段成比例.
平行于三角形一边的直线截其他两边所得的对应线段成比例.
例 如图,已AA1//BB1//CC1,AB=2,BC=3,A1B1=1.5, 求B1C1的长.
如图,AC,BD相交于点O,直线MN过点O,且BA//MN//CD,已知OA=3,OB=1,OD=2,
求OC的长.
解:
如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,若AB=3,AD=2,EC=1.8,
求AC的长.
M
N
两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也 .?
用几何语言表述:如图3-2-5,
∵AD∥BE∥CF,且AB=BC,
∴DE=EF.
平行线等分线段基本事实
相等
[点拨]
平行线等分线段基本事实是证明两条线段相等的依据之一.
图3-2-5
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}?
内容
图例
基本
事实
两条直线被一组平行线所截,所得的 成比例?
推论
平行于三角形一边的直线截其他两边,所得的 成比例?
平行线分线段成比例
对应线段
对应线段
3.2 平行线分线段成比例
在四条线段中, 如果其中两条线段的比等于另外两条线段的比, 那么这四条线段叫作成比例线段, 简称为比例线段.
平行四边形、矩形、正方形、菱形中的四条线段也分别都是成比例线段.
如果能将一条线段AB分成不相等的两部分,使较短线段CB与较长线段AC的比等于线段AC与原线段AB的比,那么称线段AB被点C黄金分割(golden section),点C叫作线段AB的黄金分割点, 较长线段AC与原线段AB的比叫作黄金分割比.
任意线段都有黄金分割点,如何找到它呢?
对于一条给定的线段AB,找出它的黄金分割点的作法如下:
(1)过点B作AB的垂线,并在垂线上取BC= AB;
(2)连接AC,以点C为圆心,CB为半径画弧,交AC于点E;
(3)以点A为圆心,AE为半径画弧,交AB 于点P.
则点P为所求作的线段AB的黄金分割点.
互相平行
下图是一架梯子的示意图,请根据生活常识判断AA1,BB1,CC1,DD1的位置关系.
a
b
c
下图是一架梯子的示意图,由生活常识可以道:AA1,BB1,CC1,DD1互相平行,且若AB=BC,你能猜想出什么结果呢?
a
b
c
如图,已知直线a∥b∥c.直线l1,l2被直线a,b,c截得的线段分别为AB,BC和A1B1,B1C1,且AB=BC,要证明A1B1=B1C1,能不做辅助线证明吗?如果必须做辅助线,你考虑怎么做呢?
过点B作直线l3//l2,分别与直线a,c相交于点A2,C2,由于a//b//c,l3//l2,因此由
“夹在两平行线间的
平行线段相等”可知
A2B=A1B1,
BC2=B1C1.
a
b
c
a
b
c
两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
a
b
c
相等,都等于1.
a
b
c
,则把线段AB二等分,分点D.
过点D作直线d∥a,交l2于点D1.如图:
把线段BC三等分.
三等分点为E,F,分
别过点E,F作直线
e∥a,f∥a,分别交
l2于点E1,F1.
e
a
b
c
f
d
证明:
e
a
b
c
f
d
a
b
c
两条直线被一组直线所截,所得的对应线段成比例.
我们把以上基本事实简称为平行线分线段成比例.
平行于三角形一边的直线截其他两边所得的对应线段成比例.
例 如图,已AA1//BB1//CC1,AB=2,BC=3,A1B1=1.5, 求B1C1的长.
如图,AC,BD相交于点O,直线MN过点O,且BA//MN//CD,已知OA=3,OB=1,OD=2,
求OC的长.
解:
如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,若AB=3,AD=2,EC=1.8,
求AC的长.
M
N
两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也 .?
用几何语言表述:如图3-2-5,
∵AD∥BE∥CF,且AB=BC,
∴DE=EF.
平行线等分线段基本事实
相等
[点拨]
平行线等分线段基本事实是证明两条线段相等的依据之一.
图3-2-5
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}?
内容
图例
基本
事实
两条直线被一组平行线所截,所得的 成比例?
推论
平行于三角形一边的直线截其他两边,所得的 成比例?
平行线分线段成比例
对应线段
对应线段
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
