3.4.1 相似三角形的判定-3同步课件-2021-2022学年湘教版数学九年级上册(共17张ppt)
文档属性
| 名称 | 3.4.1 相似三角形的判定-3同步课件-2021-2022学年湘教版数学九年级上册(共17张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 332.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 18:36:04 | ||
图片预览



文档简介
第三章 图形的相似
3.4.1 相似三角形的判定
第3课时 相似三角形的判定定理二
相似三角形的性质:
相似三角形的对应角相等,对应边成比例.
我们把三个角对应相等,且三条边对应成比例的
两个三角形叫作相似三角形.
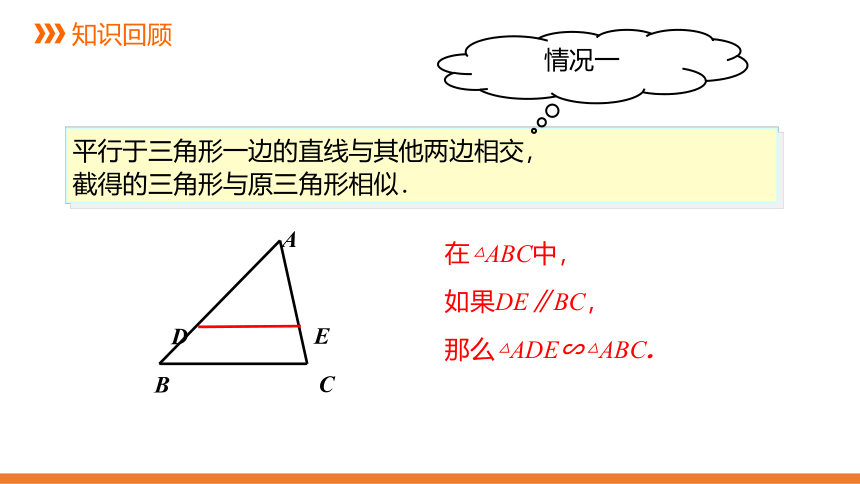
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC.
情况一
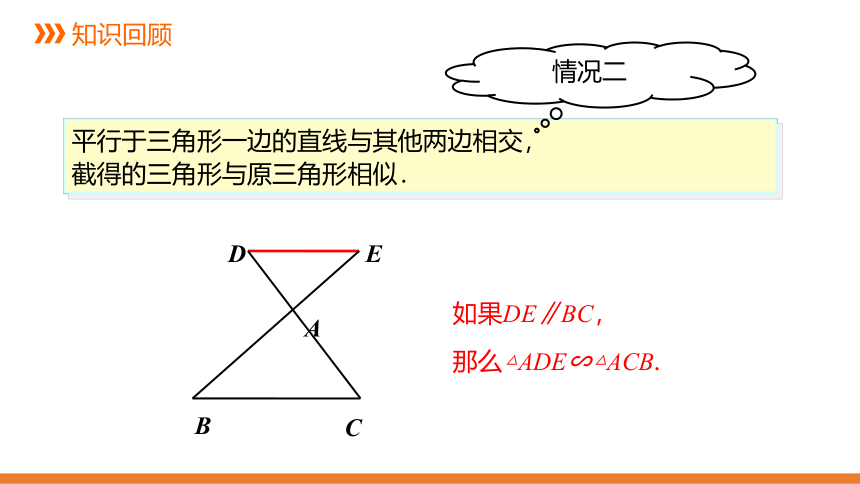
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
情况二
D
E
A
C
B
如果DE∥BC,
那么△ADE∽△ACB.
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC.
情况三
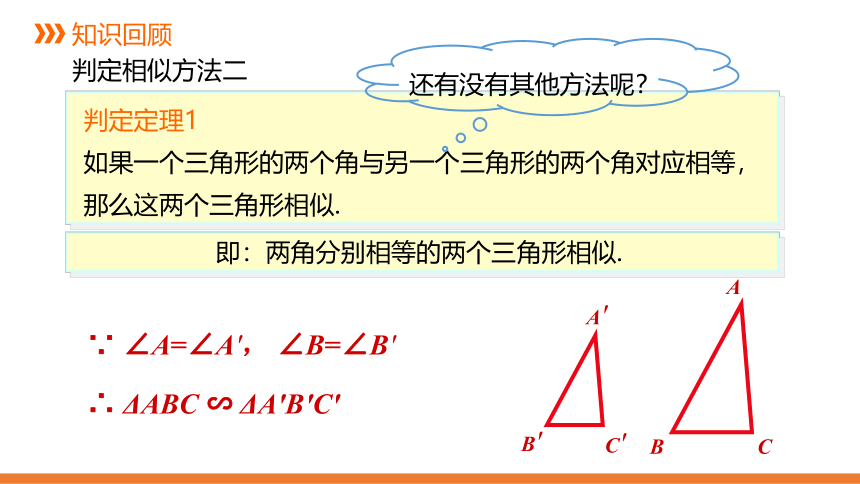
判定定理1
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
即:两角分别相等的两个三角形相似.
判定相似方法二
还有没有其他方法呢?
C
A
B
A'
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
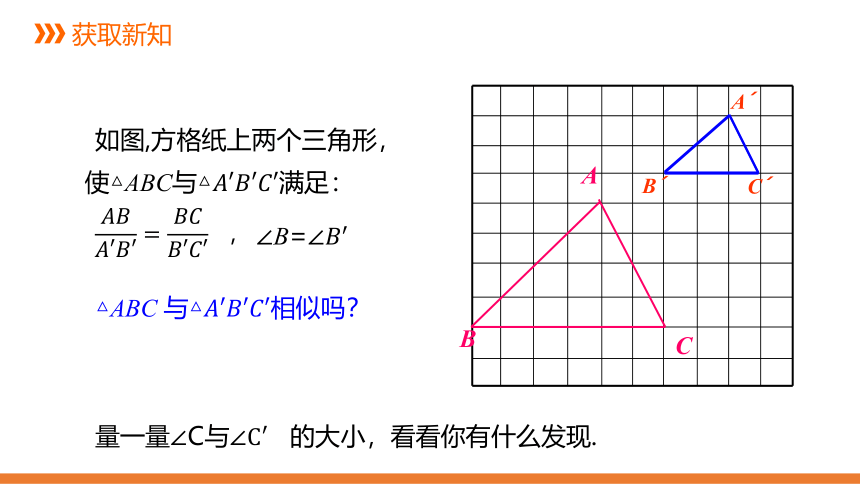
A
B
C
△ABC 与△????′????′????′相似吗?
?
如图,方格纸上两个三角形,
使△ABC与△????′????′????′满足:
?
????????????′????′=????????????′????′???,
?
∠B=∠????′
?
量一量∠C与∠C′ 的大小,看看你有什么发现.
?
B?
A?
C?
思考:如果三角形两边对应成比例,且夹角相等请验证这两个三角形是相似的.
已知:在△ABC 和△ A'B'C’ 中, ????′????′????????=????′????′????????,? ∠A=∠A'
?
求证:ΔABC∽ △ A'B'C'
A'
B'
C'
A
B
C
证明:在△ABC的边AB(或延长线)上
截取AD=A′B′,过点D作DE∥BC交AC于点E.
A'
B'
C'
A
B
C
E
D
∴ △ADE∽△ABC,????????????????=????????????????,
?
∵????????=????′????′, ????′????′????????=????′????′????????,
?
∴ADAB=AEAC=A′C′AC,
?
∴????????=????′????′,
?
思考:如果三角形两边对应成比例,且夹角相等请验证这两个三角形是相似的.
已知:在△ABC 和△ A'B'C' 中, ????′????′????????=????′????′????????, ∠A=∠A′
?
求证: ΔABC∽ △ A'B'C'
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,过点D作DE∥BC交AC于点E.
A'
B'
C'
A
B
C
E
D
∴△ADE ≌ △ A'B'C'
∴△ A'B'C' ∽△ABC
∵∠A=∠A′
判定定理2
如果一个三角形的两条边与另一个三角形的两条边对应成比例,且夹角相等,那么这两个三角形相似.
A
B
C
????′
?
????′
?
????′
?
那么 ΔABC ∽ ΔA'B'C'
即:两边对应成比例且夹角相等的两个三角形相似.
如果 ????′????′????????=????′????′???????? , ∠A=∠A'
?
例5:在△ABC与△DEF中,已知∠C= ∠F =70° AC=3.5cm,BC=2.5cm,DF=2.1cm,EF=1.5cm.
求证:△ABC∽△ DEF.
A
B
C
D
E
F
A
B
C
D
E
F
例6:在△ABC中,CD是边AB上的高,且????????????????=????????????????
求证:∠ACB=90°
?
A
B
D
C
如图,已知∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.
求证:△ABC∽△AED.
∵AB=20.4,AC=48,
AE=17,AD=40,
∴????????????????=20.417=1.2 , ????????????????=4840=1.2,
∴????????????????=????????????????.
∵∠BAC=∠EAD,
∴△ABC∽△AED.
?
证明:
相似三角形的判定定理2
如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.
可简单说成:两边 且 相等的两个三角形相似.
成比例
夹角
3.4.1 相似三角形的判定
第3课时 相似三角形的判定定理二
相似三角形的性质:
相似三角形的对应角相等,对应边成比例.
我们把三个角对应相等,且三条边对应成比例的
两个三角形叫作相似三角形.
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC.
情况一
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
情况二
D
E
A
C
B
如果DE∥BC,
那么△ADE∽△ACB.
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC.
情况三
判定定理1
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
即:两角分别相等的两个三角形相似.
判定相似方法二
还有没有其他方法呢?
C
A
B
A'
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
A
B
C
△ABC 与△????′????′????′相似吗?
?
如图,方格纸上两个三角形,
使△ABC与△????′????′????′满足:
?
????????????′????′=????????????′????′???,
?
∠B=∠????′
?
量一量∠C与∠C′ 的大小,看看你有什么发现.
?
B?
A?
C?
思考:如果三角形两边对应成比例,且夹角相等请验证这两个三角形是相似的.
已知:在△ABC 和△ A'B'C’ 中, ????′????′????????=????′????′????????,? ∠A=∠A'
?
求证:ΔABC∽ △ A'B'C'
A'
B'
C'
A
B
C
证明:在△ABC的边AB(或延长线)上
截取AD=A′B′,过点D作DE∥BC交AC于点E.
A'
B'
C'
A
B
C
E
D
∴ △ADE∽△ABC,????????????????=????????????????,
?
∵????????=????′????′, ????′????′????????=????′????′????????,
?
∴ADAB=AEAC=A′C′AC,
?
∴????????=????′????′,
?
思考:如果三角形两边对应成比例,且夹角相等请验证这两个三角形是相似的.
已知:在△ABC 和△ A'B'C' 中, ????′????′????????=????′????′????????, ∠A=∠A′
?
求证: ΔABC∽ △ A'B'C'
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,过点D作DE∥BC交AC于点E.
A'
B'
C'
A
B
C
E
D
∴△ADE ≌ △ A'B'C'
∴△ A'B'C' ∽△ABC
∵∠A=∠A′
判定定理2
如果一个三角形的两条边与另一个三角形的两条边对应成比例,且夹角相等,那么这两个三角形相似.
A
B
C
????′
?
????′
?
????′
?
那么 ΔABC ∽ ΔA'B'C'
即:两边对应成比例且夹角相等的两个三角形相似.
如果 ????′????′????????=????′????′???????? , ∠A=∠A'
?
例5:在△ABC与△DEF中,已知∠C= ∠F =70° AC=3.5cm,BC=2.5cm,DF=2.1cm,EF=1.5cm.
求证:△ABC∽△ DEF.
A
B
C
D
E
F
A
B
C
D
E
F
例6:在△ABC中,CD是边AB上的高,且????????????????=????????????????
求证:∠ACB=90°
?
A
B
D
C
如图,已知∠BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.
求证:△ABC∽△AED.
∵AB=20.4,AC=48,
AE=17,AD=40,
∴????????????????=20.417=1.2 , ????????????????=4840=1.2,
∴????????????????=????????????????.
∵∠BAC=∠EAD,
∴△ABC∽△AED.
?
证明:
相似三角形的判定定理2
如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.
可简单说成:两边 且 相等的两个三角形相似.
成比例
夹角
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
