3.4.1 相似三角形的判定-4同步课件-2021-2022学年湘教版数学九年级上册(共18张ppt)
文档属性
| 名称 | 3.4.1 相似三角形的判定-4同步课件-2021-2022学年湘教版数学九年级上册(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 520.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 00:00:00 | ||
图片预览




文档简介
第三章 图形的相似
3.4.1 相似三角形的判定
第4课时 相似三角形的判定定理三
相似三角形的性质:
相似三角形的对应角相等,对应边成比例.
我们把三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形.
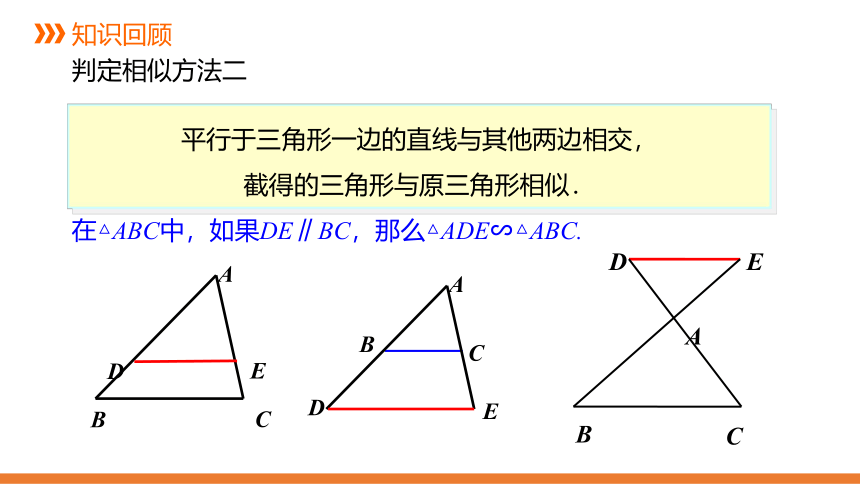
判定相似方法一
判定相似方法二
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,如果DE∥BC,那么△ADE∽△ABC.
D
E
A
C
B
A
B
C
D
E
判定定理1
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
C
A
B
A'
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
相似三角形判定方法三
即:两角分别相等的两个三角形相似 .
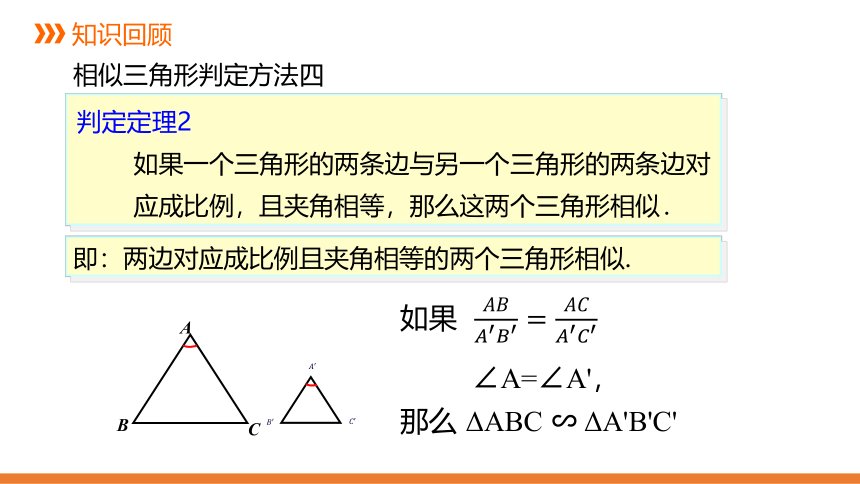
判定定理2
如果一个三角形的两条边与另一个三角形的两条边对应成比例,且夹角相等,那么这两个三角形相似.
A
B
C
????′
?
????′
?
????′
?
如果 ????????????′????′=????????????′????′
∠A=∠A',
?
那么 ΔABC ∽ ΔA'B'C'
即:两边对应成比例且夹角相等的两个三角形相似.
相似三角形判定方法四
A
B
C
C'
B'
A'
是否存在三边对应成比例,两三角形相似呢?
是否存在 ΔABC ∽ ΔA'B'C'?
????′????′????????=????′????′????????=????′????′????????
?
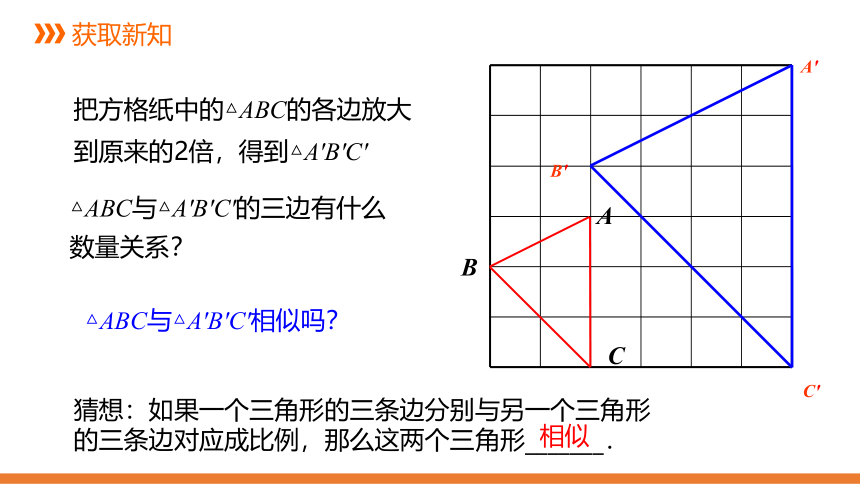
猜想:如果一个三角形的三条边分别与另一个三角形的三条边对应成比例,那么这两个三角形_______.
相似
A
B
C
把方格纸中的△ABC的各边放大到原来的2倍,得到△A'B'C'
A'
C'
B'
△ABC与△A'B'C'相似吗?
△ABC与△A'B'C'的三边有什么数量关系?
思考:如果三角形三条边对应成比例,请验证这两个三角形是相似的.
已知:在△ABC 和△ A'B'C' 中, ????′????′????????=????′????′????????=????′????′????????
?
求证: ΔABC∽ △ A'B'C'
A'
B'
C'
A
B
C
D
E
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
A'
B'
C'
A
B
C
D
E
过点D作DE∥BC交AC于点E.
∴ △ADE∽△ABC,
????????????????=????????????????=????????????????
?
∵ ????????=????′????′,∴????????????????=????′????′????????
?
又 ?????′????′????????=????′????′????????=????′????′????????
?
∴ ????????????????=????′????′????????,????????????????=????′????′????????.
?
因此?????????=????′????′,????????=????′????′.
?
∴△ ????′????′????′∽△ABC
?
∴ △ADE≌△????′????′????′
?
那么 △ABC∽△????′????′????′
?
判定定理3
如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.
即:三边成比例的两个三角形相似.
如果 ????????????′????′=????????????′????′=????????????′????′
?
已知△ABC 和 △DEF,根据下列条件判断它们是否相似.
(3) AB=12, BC=15, AC=24
DE=16, EF=20, DF=30
(2) AB=4, BC=8, AC=10
DE=20, EF=16, DF=8
(1) AB=3, BC=4, AC=6
DE=6, EF=8, DF=9
是
否
否
(大对大,小对小,中对中)
一“排”
二“算”
三“判”
将每个三角形的三边的长度按大小顺序排列
利用三边判断两个三角形是否相似的步骤
计算最长边与最长边的比,较长边与较长边的比,最短边与最短边的比
由比值是否相等判断两个三角形是否相似
【1】两个直角三角形一定相似吗?
两个等腰直角三角形呢?为什么?
1.所有的直角三角形不都相似;
2.所有的等腰直角三角形都相似.
A
B
C
D
E
F
【2】两个等腰三角形一定相似吗?
两个等边三角形呢?为什么?
1.所有的等腰三角形不都相似;
2.所有的等边三角形都相似.
依据下面的条件,判定△ABC与△A'B'C'是否相似.若相似,请给出证明;若不相似,请说明理由.
(1)AB=1,AC=1.5,BC=2,A'B'=12,A'C'=8,C'B'=16;
(2)BC=2,AC=3,AB=4,B'C'=2,A'C'=3,A'B'=2.
?
解:(1)相似.
∵????????????′????′ = 18 , ????????????′????′ = 1.512 = 18 ,
????????????′????′ = 216 = 18 ,
∴????????????′????′ = ????????????′????′ = ????????????′????′ ,
∴△ABC∽△A'C'B'.
?
(2)不相似.
将△ABC 的三边从小到大排列为
BC=2,AC=3,AB=4,
将△A'B'C' 的三边从小到大排列为
B‘C’=2,A‘C’=3,A'B'=2.
∵????????????′????′ = 22 = 2 , ????????????′????′ = 33 = 3,
????????????′????′=42=2,∴????????????′????′ ≠ ????????????′????′ ≠ ????????????′????′.
∴△ABC与△A'B'C'不相似.
?
∵????????????????=????????????????=????????????????,
∴△ABC∽△ADE.
∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-
∠DAC,
即∠BAD=∠CAE.
∵∠BAD=20°,∴∠CAE=20°.
?
如图,在△ABC和△ADE,ABAD=BCDE=ACAE,∠BAD=20°,求∠CAE的度数.
解:
相似三角形的判定定理中,
预备定理(平行截相似)与判定定理1(两角分别相等判定相似)运用最广,
其次是判定定理2(两边成比例,夹角相等判定相似),
相比之下,判定定理3(三边成比例判定相似)用得较少.?
在找三角形相似的条件时,
优先考虑角相等或平行关系,
其次考虑边成比例.
3.4.1 相似三角形的判定
第4课时 相似三角形的判定定理三
相似三角形的性质:
相似三角形的对应角相等,对应边成比例.
我们把三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形.
判定相似方法一
判定相似方法二
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,如果DE∥BC,那么△ADE∽△ABC.
D
E
A
C
B
A
B
C
D
E
判定定理1
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
C
A
B
A'
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
相似三角形判定方法三
即:两角分别相等的两个三角形相似 .
判定定理2
如果一个三角形的两条边与另一个三角形的两条边对应成比例,且夹角相等,那么这两个三角形相似.
A
B
C
????′
?
????′
?
????′
?
如果 ????????????′????′=????????????′????′
∠A=∠A',
?
那么 ΔABC ∽ ΔA'B'C'
即:两边对应成比例且夹角相等的两个三角形相似.
相似三角形判定方法四
A
B
C
C'
B'
A'
是否存在三边对应成比例,两三角形相似呢?
是否存在 ΔABC ∽ ΔA'B'C'?
????′????′????????=????′????′????????=????′????′????????
?
猜想:如果一个三角形的三条边分别与另一个三角形的三条边对应成比例,那么这两个三角形_______.
相似
A
B
C
把方格纸中的△ABC的各边放大到原来的2倍,得到△A'B'C'
A'
C'
B'
△ABC与△A'B'C'相似吗?
△ABC与△A'B'C'的三边有什么数量关系?
思考:如果三角形三条边对应成比例,请验证这两个三角形是相似的.
已知:在△ABC 和△ A'B'C' 中, ????′????′????????=????′????′????????=????′????′????????
?
求证: ΔABC∽ △ A'B'C'
A'
B'
C'
A
B
C
D
E
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
A'
B'
C'
A
B
C
D
E
过点D作DE∥BC交AC于点E.
∴ △ADE∽△ABC,
????????????????=????????????????=????????????????
?
∵ ????????=????′????′,∴????????????????=????′????′????????
?
又 ?????′????′????????=????′????′????????=????′????′????????
?
∴ ????????????????=????′????′????????,????????????????=????′????′????????.
?
因此?????????=????′????′,????????=????′????′.
?
∴△ ????′????′????′∽△ABC
?
∴ △ADE≌△????′????′????′
?
那么 △ABC∽△????′????′????′
?
判定定理3
如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.
即:三边成比例的两个三角形相似.
如果 ????????????′????′=????????????′????′=????????????′????′
?
已知△ABC 和 △DEF,根据下列条件判断它们是否相似.
(3) AB=12, BC=15, AC=24
DE=16, EF=20, DF=30
(2) AB=4, BC=8, AC=10
DE=20, EF=16, DF=8
(1) AB=3, BC=4, AC=6
DE=6, EF=8, DF=9
是
否
否
(大对大,小对小,中对中)
一“排”
二“算”
三“判”
将每个三角形的三边的长度按大小顺序排列
利用三边判断两个三角形是否相似的步骤
计算最长边与最长边的比,较长边与较长边的比,最短边与最短边的比
由比值是否相等判断两个三角形是否相似
【1】两个直角三角形一定相似吗?
两个等腰直角三角形呢?为什么?
1.所有的直角三角形不都相似;
2.所有的等腰直角三角形都相似.
A
B
C
D
E
F
【2】两个等腰三角形一定相似吗?
两个等边三角形呢?为什么?
1.所有的等腰三角形不都相似;
2.所有的等边三角形都相似.
依据下面的条件,判定△ABC与△A'B'C'是否相似.若相似,请给出证明;若不相似,请说明理由.
(1)AB=1,AC=1.5,BC=2,A'B'=12,A'C'=8,C'B'=16;
(2)BC=2,AC=3,AB=4,B'C'=2,A'C'=3,A'B'=2.
?
解:(1)相似.
∵????????????′????′ = 18 , ????????????′????′ = 1.512 = 18 ,
????????????′????′ = 216 = 18 ,
∴????????????′????′ = ????????????′????′ = ????????????′????′ ,
∴△ABC∽△A'C'B'.
?
(2)不相似.
将△ABC 的三边从小到大排列为
BC=2,AC=3,AB=4,
将△A'B'C' 的三边从小到大排列为
B‘C’=2,A‘C’=3,A'B'=2.
∵????????????′????′ = 22 = 2 , ????????????′????′ = 33 = 3,
????????????′????′=42=2,∴????????????′????′ ≠ ????????????′????′ ≠ ????????????′????′.
∴△ABC与△A'B'C'不相似.
?
∵????????????????=????????????????=????????????????,
∴△ABC∽△ADE.
∴∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-
∠DAC,
即∠BAD=∠CAE.
∵∠BAD=20°,∴∠CAE=20°.
?
如图,在△ABC和△ADE,ABAD=BCDE=ACAE,∠BAD=20°,求∠CAE的度数.
解:
相似三角形的判定定理中,
预备定理(平行截相似)与判定定理1(两角分别相等判定相似)运用最广,
其次是判定定理2(两边成比例,夹角相等判定相似),
相比之下,判定定理3(三边成比例判定相似)用得较少.?
在找三角形相似的条件时,
优先考虑角相等或平行关系,
其次考虑边成比例.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
