3.4.1 相似三角形的判定-2---同步课件 2021-2022学年数学九年级湘教版上册(共17张ppt)
文档属性
| 名称 | 3.4.1 相似三角形的判定-2---同步课件 2021-2022学年数学九年级湘教版上册(共17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 361.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 18:43:30 | ||
图片预览




文档简介
第三章 图形的相似
3.4.1 相似三角形的判定
第2课时 相似三角形的判定定理一
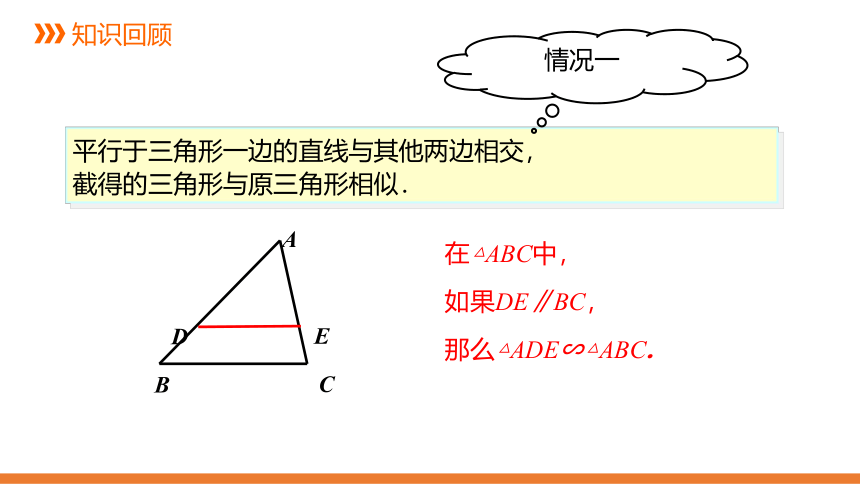
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC.
情况一
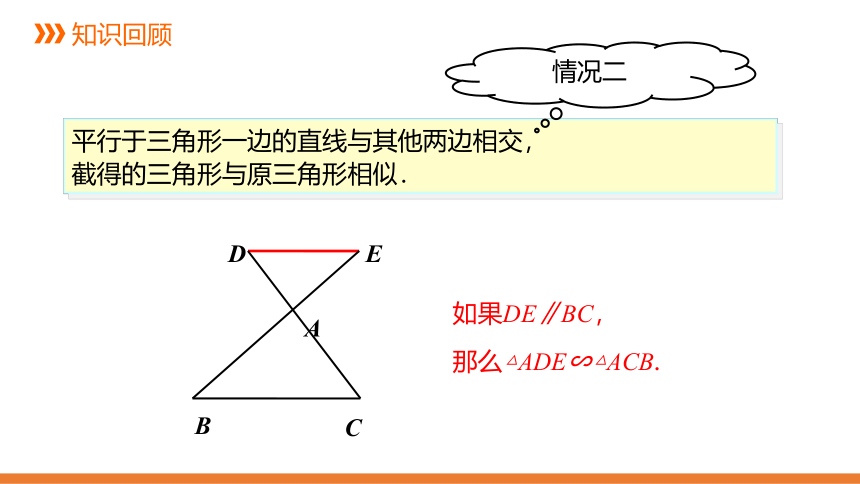
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
情况二
D
E
A
C
B
如果DE∥BC,
那么△ADE∽△ACB.
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC.
情况三
思考:三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等.
观察你与老师的直角三角尺(30° 与60°) ,
会相似吗?
这两个三角形的三个内角的大小有什么关系?
相
似
画两个三角形 ,使每个三角形的三个角的度数分别为60°,45°, 75°
①分别量出两个三角形三边的长度;
②这两个三角形相似吗?
猜想:如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
相似
一定需三个角吗?
观察
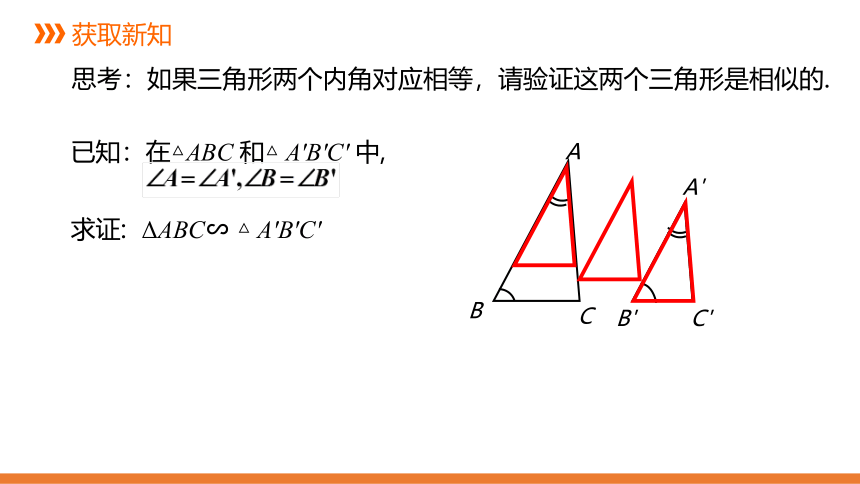
思考:如果三角形两个内角对应相等,请验证这两个三角形是相似的.
A
B
C
A'
C'
B'
求证: ΔABC∽ △ A'B'C'
已知:在△ABC 和△ A'B'C' 中,
分析:
要证两个三角形相似,目前只有两个途径:
一个是三角形相似的定义(显然条件不具备);
二是利用平行线来判定三角形相似的定理.
A
B
C
A'
C'
B'
A
B
C
A'
C'
B'
D
E
证明:在ΔABC的边AB、AC上,分别
截取AD=A'B',AE=A'C' ,连结DE.
∵ AD=A'B ,∠A=∠A',AE=A'C'
∴ ΔA DE≌Δ A'B'C' ,
∴ ∠ADE=∠B',
又∵ ∠B'=∠B,
∴ ∠ADE=∠B,
∴ DE//BC,
∴ ΔADE∽ΔABC.
∴ ΔA'B'C'∽ΔABC.
求证: ΔABC∽ △ A'B'C'
已知:在△ABC 和△ A'B'C' 中,
判定定理1
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
C
A
B
A'
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
即:两角分别相等的两个三角形相似.
下面每组的两个三角形是否相似?为什么?
①
②
③
④
70o
50o
30o
30o
30o
30o
55o
30o
60o
50o
例3:在△ABC中, ∠C=90° 从点D分别做边AB,BC的垂线,垂足分别为E,F.DF与AB交于点H. 求证:△DEH∽△ BCA.
△DEH∽△ BCA.
// AC
B
A
C
H
F
E
D
例4:在Rt△ABC与Rt△DEF中, 若
求EF的长.
△DEF∽△ ABC
A
C
B
D
F
E
下列各组三角形中,不一定相似的是 ( )
A.两个等腰直角三角形
B.底角为40°的两个等腰三角形
C.有一个角为30°的两个直角三角形
D.有一个角为30°的两个等腰三角形
D
如图,在Rt△ABC,∠C=90°, AB=14,AC=7.D是BC上一点,BD=8,DE⊥AB,垂足为E.求线段DE的长.
∵DE⊥AB,
∴∠DEB=90°,
∴∠DEB=∠C.
又∵∠B=∠B,
∴△DBE∽△ABC,
∴????????????????=????????????????,
即????????7=814,
∴DE=4.
?
解:
两角 的两个三角形相似.?
几何语言:
在△ABC与△DEF,
∵∠A=∠D,∠B=∠E,
∴△ABC∽△DEF.
[点拨]如图:利用两角分别相等判定三角形相似的常见基本图形.
分别相等
相似三角形的判定定理1
3.4.1 相似三角形的判定
第2课时 相似三角形的判定定理一
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC.
情况一
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
情况二
D
E
A
C
B
如果DE∥BC,
那么△ADE∽△ACB.
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,
如果DE∥BC,
那么△ADE∽△ABC.
情况三
思考:三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等.
观察你与老师的直角三角尺(30° 与60°) ,
会相似吗?
这两个三角形的三个内角的大小有什么关系?
相
似
画两个三角形 ,使每个三角形的三个角的度数分别为60°,45°, 75°
①分别量出两个三角形三边的长度;
②这两个三角形相似吗?
猜想:如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
相似
一定需三个角吗?
观察
思考:如果三角形两个内角对应相等,请验证这两个三角形是相似的.
A
B
C
A'
C'
B'
求证: ΔABC∽ △ A'B'C'
已知:在△ABC 和△ A'B'C' 中,
分析:
要证两个三角形相似,目前只有两个途径:
一个是三角形相似的定义(显然条件不具备);
二是利用平行线来判定三角形相似的定理.
A
B
C
A'
C'
B'
A
B
C
A'
C'
B'
D
E
证明:在ΔABC的边AB、AC上,分别
截取AD=A'B',AE=A'C' ,连结DE.
∵ AD=A'B ,∠A=∠A',AE=A'C'
∴ ΔA DE≌Δ A'B'C' ,
∴ ∠ADE=∠B',
又∵ ∠B'=∠B,
∴ ∠ADE=∠B,
∴ DE//BC,
∴ ΔADE∽ΔABC.
∴ ΔA'B'C'∽ΔABC.
求证: ΔABC∽ △ A'B'C'
已知:在△ABC 和△ A'B'C' 中,
判定定理1
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
C
A
B
A'
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
即:两角分别相等的两个三角形相似.
下面每组的两个三角形是否相似?为什么?
①
②
③
④
70o
50o
30o
30o
30o
30o
55o
30o
60o
50o
例3:在△ABC中, ∠C=90° 从点D分别做边AB,BC的垂线,垂足分别为E,F.DF与AB交于点H. 求证:△DEH∽△ BCA.
△DEH∽△ BCA.
// AC
B
A
C
H
F
E
D
例4:在Rt△ABC与Rt△DEF中, 若
求EF的长.
△DEF∽△ ABC
A
C
B
D
F
E
下列各组三角形中,不一定相似的是 ( )
A.两个等腰直角三角形
B.底角为40°的两个等腰三角形
C.有一个角为30°的两个直角三角形
D.有一个角为30°的两个等腰三角形
D
如图,在Rt△ABC,∠C=90°, AB=14,AC=7.D是BC上一点,BD=8,DE⊥AB,垂足为E.求线段DE的长.
∵DE⊥AB,
∴∠DEB=90°,
∴∠DEB=∠C.
又∵∠B=∠B,
∴△DBE∽△ABC,
∴????????????????=????????????????,
即????????7=814,
∴DE=4.
?
解:
两角 的两个三角形相似.?
几何语言:
在△ABC与△DEF,
∵∠A=∠D,∠B=∠E,
∴△ABC∽△DEF.
[点拨]如图:利用两角分别相等判定三角形相似的常见基本图形.
分别相等
相似三角形的判定定理1
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
