3.4.2 相似三角形的性质-1---同步课件 2021-2022学年九年级数学湘教版上册(共20张ppt)
文档属性
| 名称 | 3.4.2 相似三角形的性质-1---同步课件 2021-2022学年九年级数学湘教版上册(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 363.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-25 18:44:29 | ||
图片预览






文档简介
第三章 图形的相似
3.4.2 相似三角形的性质
第1课时 与相似三角形的三线有关的性质
相似三角形的性质:
相似三角形的对应角相等,对应边成比例.
我们把三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形.
判定相似方法一
判定相似方法二
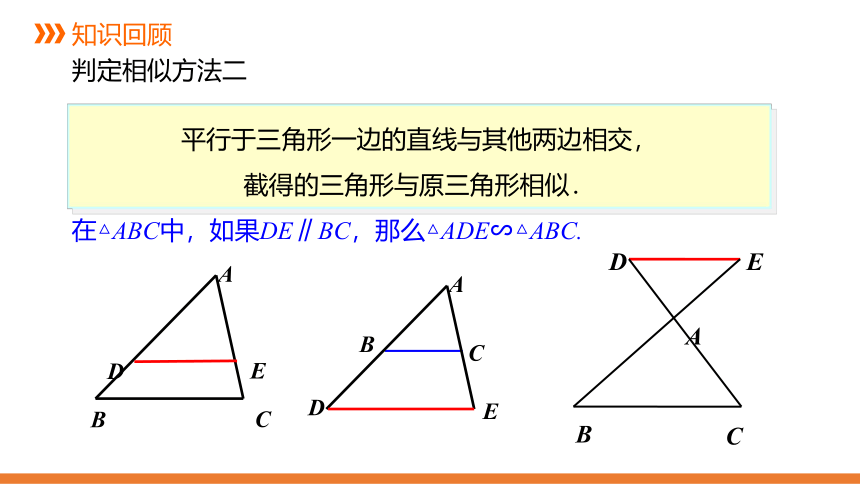
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,如果DE∥BC,那么△ADE∽△ABC.
D
E
A
C
B
A
B
C
D
E
判定定理1
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
C
A
B
A'
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
相似三角形判定方法三
即:两角分别相等的两个三角形相似 .
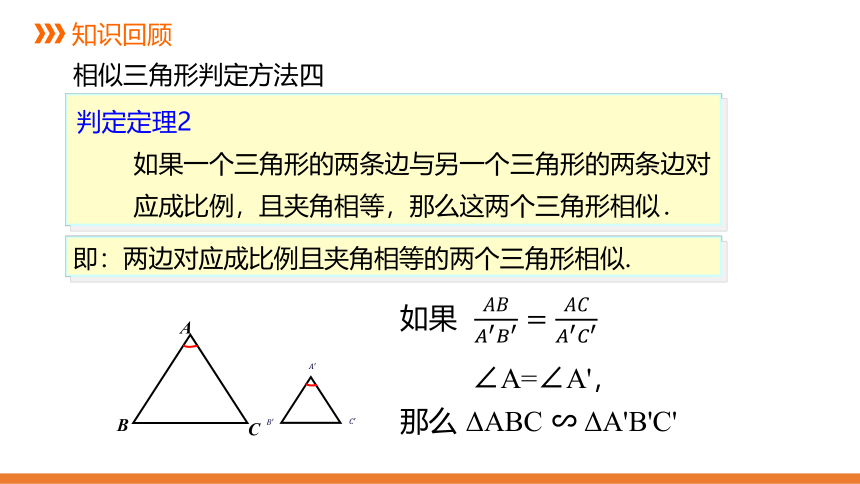
判定定理2
如果一个三角形的两条边与另一个三角形的两条边对应成比例,且夹角相等,那么这两个三角形相似.
A
B
C
????′
?
????′
?
????′
?
如果 ????????????′????′=????????????′????′
∠A=∠A',
?
那么 ΔABC ∽ ΔA'B'C'
即:两边对应成比例且夹角相等的两个三角形相似.
相似三角形判定方法四
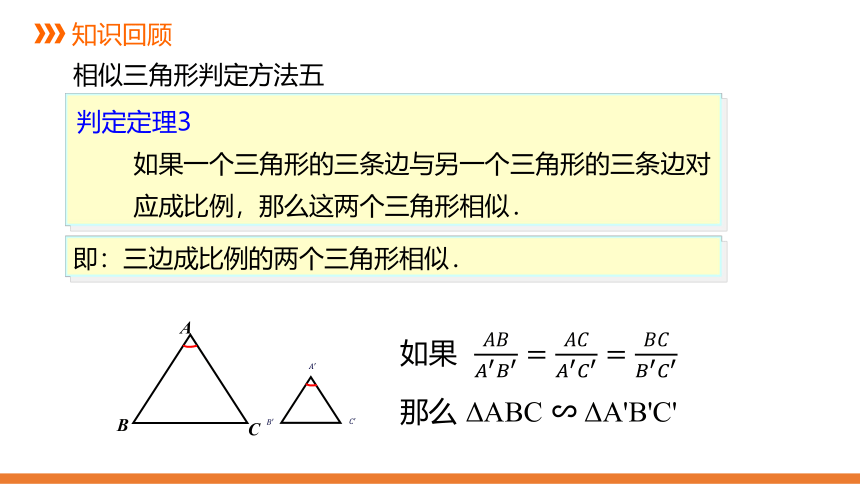
判定定理3
如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.
A
B
C
????′
?
????′
?
????′
?
如果 ????????????′????′=????????????′????′ = ????????????′????′
?
那么 ΔABC ∽ ΔA'B'C'
即:三边成比例的两个三角形相似.
相似三角形判定方法五
1.所有的直角三角形不都相似;
2.所有的等腰直角三角形都相似.
1.所有的等腰三角形不都相似;
2.所有的等边三角形都相似.
两句话
全等三角形与相似三角形性质比较
全等三角形
相似三角形
对应边的比等于相似比
对应角相等
周长……?
面积……?
对应高……?
对应中线……?
对应角平分线……?
对应边相等
对应角相等
周长相等
面积相等
对应高相等
对应中线相等
对应角平分线相等
∵△A?B?C?∽△ABC,
∴ ∠B′= ∠B.
又∵ ∠A ′ D ′ B ′ =∠ADB =90°,
∴△ A ′ B ′ D′ ∽△ABD. (两角对应相等的两个三角形相似)
从而????′????′?????????=?????′????′????????=k
?
(相似三角形的对应边成比例)
那么 ????′????′?????????=?????′????′????????吗?
?
D′
C′
D
A
B
A′
B′
┓
┓
分别作BC,B??????上的高AD,??????????.
?
问题4 :若△???????????????∽ △ABC,相似比为k,
那么它们的周长比是多少?面积比是多少?
?
相似三角形对应高的比等于相似比.
D'
A'
B'
C'
D
A
B
C
那么
????????????′????′=?
?
问题2:AD和A'D'分别是△ABC和△A'B'C'的角平分线,设相似比为k
你能有条理地表达理由吗?
如图,△ ????′????′????′?∽△ABC, AD, ????′????′分别为角平分线.
求证:
?
????′????′?????????=?????′????′????????.
?
D'
A'
B'
C'
D
A
B
C
证明∵△ ????′????′????′?∽△ABC,
?
∴ ∠B′= ∠B, ∠ B ′ A ′ C ′ = ∠BAC .
又AD, A ′ D ′分别为角平分线
∴△ A′B′D′∽△ABD.
从而????′????′?????????=?????′????′????????.
?
∴ ∠BAD= 12∠BAC
= 12?∠ B′A′C′= ∠B′A′D.
?
相似三角形对应高的比等于相似比.
相似三角形对应角平分线的比等于相似比.
那么
????????????′????′=?
?
问题3:AD和A'D'分别是△ABC和△A'B'C'的中线,设相似比为k,
你能证明吗?
D
A
B
D'
A'
B'
C'
如图,△????′????′????′∽△ABC, AD,????′????′分别为三角形的中线.
求证:????′????′?????????=?????′????′????????.
?
证明:
参考角平分线的证明过程,请同学们自己完成
D
A
B
D'
A'
B'
C'
C
相似三角形对应中线的比等于相似比.
相似三角形对应高的比等于相似比.
相似三角形对应角平分线的比等于相似比.
1.已知△ABC∽△A'B'C',AD、A 'D '分别是对应边BC、B 'C '上的高,若BC=8cm, B 'C '=6cm,AD=4cm,则A 'D ' 等于( )
A. 16cm B. 12 cm C. 3 cm D. 6 cm
2.两个相似三角形对应高的比为3∶7,它们的对应角平分线的比为( )
A . 7∶3 B. 49∶9 C. 9∶49 D. 3∶7
C
D
例1:CD是Rt△ABC斜边AB上的高, DE ⊥ AC 垂足为点E.已知CD=2,AB=833,AC=4,求DE的长.
?
A
B
D
C
E
解:在Rt△????′????′????′?与 Rt △ACD中,
?
∵ ∠A= ∠A, ∠ ACB = ∠ADC=90 ° .
∴△ ABC∽△ACD.
又 CD=2 , AB=833? ,AC=4,
?
又CD,DE分别为它们的斜边上的高
∴ ?????????????????=?????????????????.
?
∴ DE=3
?
如图,△ABC∽△DEF,AG,DH 分别是△ABC和△DEF的角平分线,BC=6 cm,EF=4 cm,AG=4 cm,
求DH 的长.
解 : ∵△ABC∽△DEF,BC=6cm,EF=4cm,
故????????????????=64=32,
∴ △ABC与△DEF的相似比等于32,
∴ ????????????????=32(相似三角形对应角平分线的比等于相似比).
又 ∵ AG=4 cm,
∴ DH=4×23=83(cm).
?
(1)相似三角形对应高的比等于 .?
(2)相似三角形对应的角平分线的比等于 .?
(3)相似三角形对应边上的中线的比等于 .?
相似三角形的性质
相似比
相似比
相似比
3.4.2 相似三角形的性质
第1课时 与相似三角形的三线有关的性质
相似三角形的性质:
相似三角形的对应角相等,对应边成比例.
我们把三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形.
判定相似方法一
判定相似方法二
平行于三角形一边的直线与其他两边相交,
截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,如果DE∥BC,那么△ADE∽△ABC.
D
E
A
C
B
A
B
C
D
E
判定定理1
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
C
A
B
A'
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
相似三角形判定方法三
即:两角分别相等的两个三角形相似 .
判定定理2
如果一个三角形的两条边与另一个三角形的两条边对应成比例,且夹角相等,那么这两个三角形相似.
A
B
C
????′
?
????′
?
????′
?
如果 ????????????′????′=????????????′????′
∠A=∠A',
?
那么 ΔABC ∽ ΔA'B'C'
即:两边对应成比例且夹角相等的两个三角形相似.
相似三角形判定方法四
判定定理3
如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.
A
B
C
????′
?
????′
?
????′
?
如果 ????????????′????′=????????????′????′ = ????????????′????′
?
那么 ΔABC ∽ ΔA'B'C'
即:三边成比例的两个三角形相似.
相似三角形判定方法五
1.所有的直角三角形不都相似;
2.所有的等腰直角三角形都相似.
1.所有的等腰三角形不都相似;
2.所有的等边三角形都相似.
两句话
全等三角形与相似三角形性质比较
全等三角形
相似三角形
对应边的比等于相似比
对应角相等
周长……?
面积……?
对应高……?
对应中线……?
对应角平分线……?
对应边相等
对应角相等
周长相等
面积相等
对应高相等
对应中线相等
对应角平分线相等
∵△A?B?C?∽△ABC,
∴ ∠B′= ∠B.
又∵ ∠A ′ D ′ B ′ =∠ADB =90°,
∴△ A ′ B ′ D′ ∽△ABD. (两角对应相等的两个三角形相似)
从而????′????′?????????=?????′????′????????=k
?
(相似三角形的对应边成比例)
那么 ????′????′?????????=?????′????′????????吗?
?
D′
C′
D
A
B
A′
B′
┓
┓
分别作BC,B??????上的高AD,??????????.
?
问题4 :若△???????????????∽ △ABC,相似比为k,
那么它们的周长比是多少?面积比是多少?
?
相似三角形对应高的比等于相似比.
D'
A'
B'
C'
D
A
B
C
那么
????????????′????′=?
?
问题2:AD和A'D'分别是△ABC和△A'B'C'的角平分线,设相似比为k
你能有条理地表达理由吗?
如图,△ ????′????′????′?∽△ABC, AD, ????′????′分别为角平分线.
求证:
?
????′????′?????????=?????′????′????????.
?
D'
A'
B'
C'
D
A
B
C
证明∵△ ????′????′????′?∽△ABC,
?
∴ ∠B′= ∠B, ∠ B ′ A ′ C ′ = ∠BAC .
又AD, A ′ D ′分别为角平分线
∴△ A′B′D′∽△ABD.
从而????′????′?????????=?????′????′????????.
?
∴ ∠BAD= 12∠BAC
= 12?∠ B′A′C′= ∠B′A′D.
?
相似三角形对应高的比等于相似比.
相似三角形对应角平分线的比等于相似比.
那么
????????????′????′=?
?
问题3:AD和A'D'分别是△ABC和△A'B'C'的中线,设相似比为k,
你能证明吗?
D
A
B
D'
A'
B'
C'
如图,△????′????′????′∽△ABC, AD,????′????′分别为三角形的中线.
求证:????′????′?????????=?????′????′????????.
?
证明:
参考角平分线的证明过程,请同学们自己完成
D
A
B
D'
A'
B'
C'
C
相似三角形对应中线的比等于相似比.
相似三角形对应高的比等于相似比.
相似三角形对应角平分线的比等于相似比.
1.已知△ABC∽△A'B'C',AD、A 'D '分别是对应边BC、B 'C '上的高,若BC=8cm, B 'C '=6cm,AD=4cm,则A 'D ' 等于( )
A. 16cm B. 12 cm C. 3 cm D. 6 cm
2.两个相似三角形对应高的比为3∶7,它们的对应角平分线的比为( )
A . 7∶3 B. 49∶9 C. 9∶49 D. 3∶7
C
D
例1:CD是Rt△ABC斜边AB上的高, DE ⊥ AC 垂足为点E.已知CD=2,AB=833,AC=4,求DE的长.
?
A
B
D
C
E
解:在Rt△????′????′????′?与 Rt △ACD中,
?
∵ ∠A= ∠A, ∠ ACB = ∠ADC=90 ° .
∴△ ABC∽△ACD.
又 CD=2 , AB=833? ,AC=4,
?
又CD,DE分别为它们的斜边上的高
∴ ?????????????????=?????????????????.
?
∴ DE=3
?
如图,△ABC∽△DEF,AG,DH 分别是△ABC和△DEF的角平分线,BC=6 cm,EF=4 cm,AG=4 cm,
求DH 的长.
解 : ∵△ABC∽△DEF,BC=6cm,EF=4cm,
故????????????????=64=32,
∴ △ABC与△DEF的相似比等于32,
∴ ????????????????=32(相似三角形对应角平分线的比等于相似比).
又 ∵ AG=4 cm,
∴ DH=4×23=83(cm).
?
(1)相似三角形对应高的比等于 .?
(2)相似三角形对应的角平分线的比等于 .?
(3)相似三角形对应边上的中线的比等于 .?
相似三角形的性质
相似比
相似比
相似比
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
